چند ضلعی چیست؟ — به زبان ساده

چند ضلعی یکی از انواع شکلهای هندسی است که از یک خط شکسته بسته تشکیل میشود. چندضلعیها انواع بسیار متنوعی نظیر محدب، مقعر، منتظم، غیرمنتظم، محاطی، محیطی و غیره دارند. به علاوه، این شکلهای هندسی، به طور گسترده در دنیای واقعی مورد استفاده قرار میگیرند. در این مقاله، به معرفی اجزا، انواع، روشهای رسم، فرمولها و منابع متنوع برای یادگیری مفاهیم مرتبط با چند ضلعی ها به همراه حل مثال میپردازیم.
چند ضلعی چیست؟
چندضلعی، یک شکل دوبعدی یا سطحی است که از یک خط شکسته بسته تشکیل میشود. اگر به سطح اجسام و وسایل اطراف خود دقت کنید، چندضلعیهای مختلفی را مشاهده خواهید کرد.
به عنوان مثال، سطح کتابهای درسی، معمولا به شکل یک چندضلعی به نام مستطیل است. قطعات سنگفرش پیادهروها نیز یک مثال رایج برای نمایش شکلهای چندضلعی محسوب میشود.

چندضلعی، مجموعهای از چندین پارهخط است. بنابراین، اگر شکلی دارای یک یا چند منحنی باشد، نمیتوان آن را به عنوان چندضلعی در نظر گرفت. به عنوان مثال، دایره و بیضی، منحنیهای بسته هستند. از اینرو، این اشکال هندسی، در گروه چندضلعیها قرار نمیگیرند.
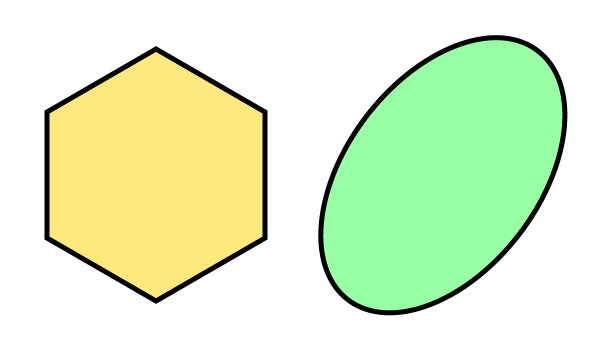
پارهخطهای تشکیلدهنده چندضلعی، یک شکل بهم پیوسته و بسته را تشکیل میدهند. در نتیجه، شکلهای باز نیز مانند منحنیهای بسته، به عنوان چندضلعی در نظر گرفته نمیشوند. تصویر زیر، سه شکل هندسی را نمایش میدهد. به علت وجود یک منحنی در شکل وسط و بسته نبودن شکل سمت چپ، این دو را نمیتوان به عنوان چندضلعی در نظر گرفت.
منظور از چندضلعی میتواند پارهخطهای تشکیلدهنده، سطح داخلی یا ترکیبی از این دو باشد. به علاوه، پارهخطهای برخی از چندضلعیها، یکدیگر را قطع میکنند.

مثال ۱: تشخیص چندضلعی
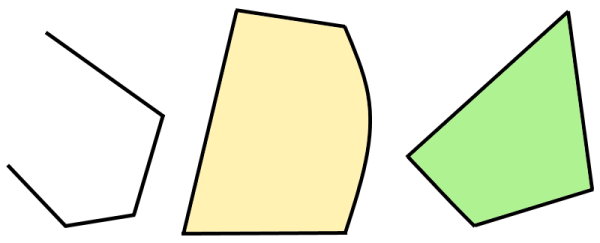
کدام یک از شکلهای زیر چند ضلعی است؟ دلیل خود را بیان کنید.

تصویر بالا، شش شکل هندسی متفاوت را نمایش میدهد.
- چندضلعی نیست. از یک منحنی بسته تشکیل شده است.
- چندضلعی نیست. با وجود دو گوشه، این شکل از اتصال دو منحنی تشکیل شده است.
- چندضلعی است. این شکل از چندین پارهخط متصل به هم تشکیل میشود.
- چندضلعی نیست. با وجود چندین پارهخط، این شکل، باز است.
- چندضلعی است. تمام شرایط یک چندضلعی از قبیل بسته بودن و متشکل شدن از چندین پارهخط را دارد.
- چندضلعی نیست. با وجود بسته بودن و متشکل شدن از چندین پارهخط، یکی از اجزای این شکل، منحنی است.
قواعد نامگذاری چند ضلعی ها
نامگذاری چندضلعیها با استفاده از علامتگذاری گوشههای آنها توسط حروف فارسی یا انگلیسی انجام میگیرد.
به عنوان مثال، چهارضلعی زیر را در نظر بگیرید.

به منظور نامگذاری چهارضلعی بالا، ابتدا گوشهها (محل برخورد ضلعهای مجاور آن) را علامت میزنیم.

سپس، در کنار هر گوشه، یک حرف دلخواه مینویسیم. بهتر است این حرفها با یکدیگر تفاوت داشته باشند.
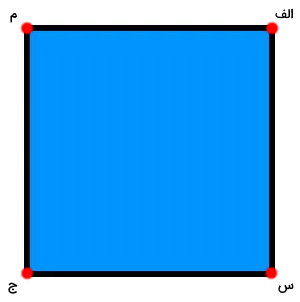
یک حرف را به عنوان نقطه شروع انتخاب میکنیم. در اینجا، ما گوشه «الف» را به عنوان اولین حرف در نظر میگیریم.
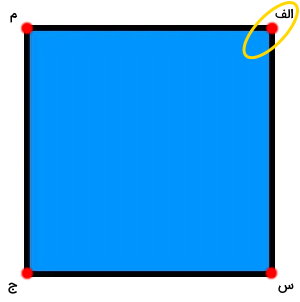
حرف بعدی را در جهت ساعتگرد (پایین-راست) یا پادساعتگرد (بالا-چپ) انتخاب میکنیم. در اینجا، جهت ساعتگرد را برای نامگذاری انتخاب میکنیم.
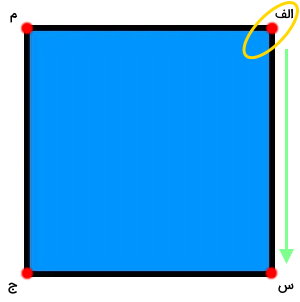
در نتیجه، حرف دوم نام چندضلعی، برابر با «س» است. انتخاب حرفهای بعدی را در همین مسیر ادامه میدهیم.
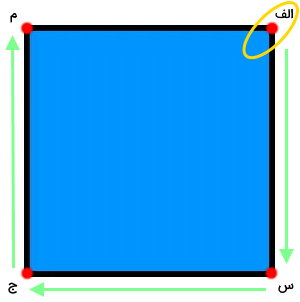
با رسیدن به آخرین گوشه، توقف میکنیم. حرفهای اول تا آخر را مینویسیم. این حرفها به صورت «الف س ج م» نوشته میشوند. بنابراین، میتوانیم چهارضلعی را با نام چهارضلعی «الف س ج م» مشخص کنیم. نقطه شروع نامگذاری یا جهت انتخاب حروف نامگذاری مهم نیستند. فقط این حروف باید به ترتیب در ادامه یکدیگر قرار داشته باشند. به عنوان مثال، شخص دیگری میتواند نام «م الف س ج» را برای چهارضلعی بالا انتخاب کند.
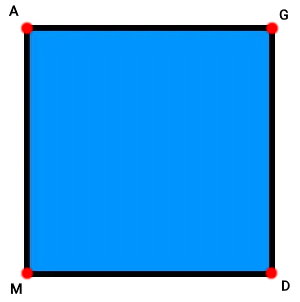
استفاده از حروف انگلیسی برای نامگذاری چندضلعیها نیز مانعی ندارد. به عنوان مثال، چندضلعی بالا را میتوان با عنوان چندضلعی «AMDG» نامگذاری کرد.
مثال ۲: تشخیص نام صحیح چندضلعی
تصویر زیر، یک پنجضلعی را نمایش میدهد. راسهای این پنجضلعی با حروف فارسی مشخص شدهاند.
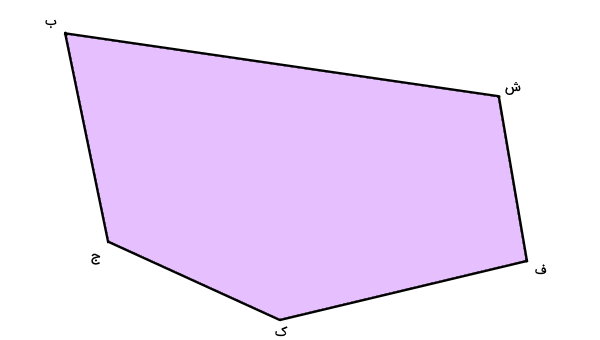
کدام یک از نامهای زیر را میتوان برای پنجضلعی بالا انتخاب کرد؟
- چندضلعی «ک ب ج ف ش»
- چندضلعی «ف ش ب ک ج»
- چندضلعی «ب ج ک ف ش»
- چندضلعی «ش ب ج ف ک»
از بین موارد بالا، گزینه ۲ و ۳ میتوانند نامهای صحیح پنجضلعی مورد سوال باشند. در گزینه ۱ و ۴، ترتیب نامگذاری و انتخاب حروف به طور کامل رعایت نشده است. به عنوان مثال در گزینه ۱، اگر میخواستیم نامگذاری را از گوشه «ب» و در جهت پادساعتگرد شروع کنیم، نام چندضلعی، «ک ف ش ب ج» میشد.
اجزای چند ضلعی ها چه هستند ؟
چندضلعیها، شکلهای هندسی پرکاربردی هستند که از اجزایی نظیر ضلع یا لبه، راس یا گوشه، زاویه (داخلی یا خارجی)، قطر و غیره تشکیل میشوند.
تصویر زیر، برخی از مهمترین اجزای یک چندضلعی را نمایش میدهد. در ادامه، به معرفی هر یک از این اجزا میپردازیم.
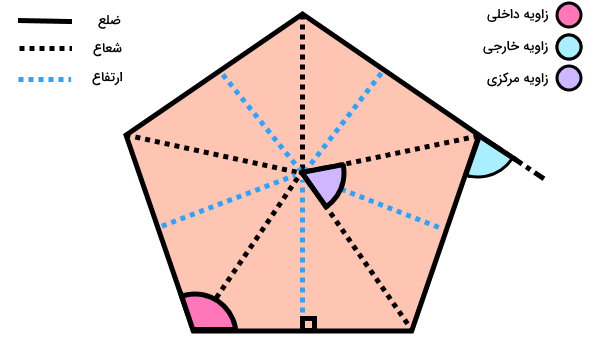
لبه چند ضلعی چیست ؟
لبهها یا ضلعها، مجموعهای از پارهخطهای تشکیلدهنده چندضلعی هستند. این اجزا، مرز بیرونی چندضلعیها را مشخص میکنند. به علاوه، اندازه لبهها به منظور تعیین محیط چندضلعی مورد استفاده قرار میگیرند. در بخشهای بعدی، به معرفی محیط و نحوه محاسبه آن خواهیم پرداخت.
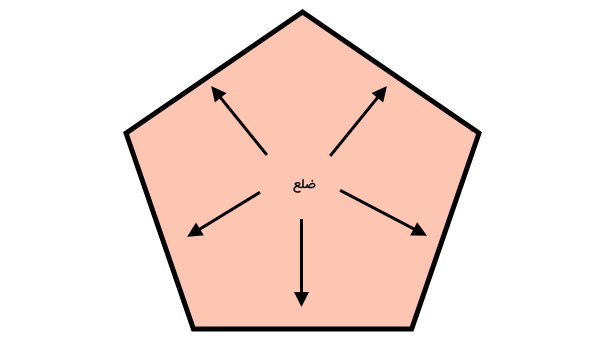
گوشه چند ضلعی چیست ؟
گوشهها یا راسها، محل برخورد ضلعهای چندضلعی به یکدیگر هستند. تعداد راسهای هر چندضلعی، برابر با تعداد ضلعهای آن است. به علاوه، راسها، زاویههای داخلی و خارجی، با توجه به محل قرارگیری راسها تعیین میشوند.
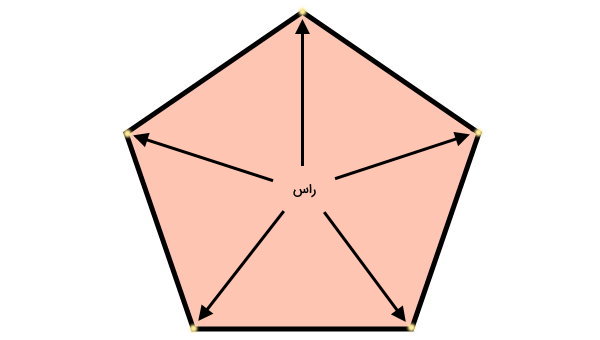
زاویه داخلی چند ضلعی چیست؟
ضلعهای یک چندضلعی، در محلی به نام گوشه یا راس به یکدیگر برخورد میکنند. به زاویه برخورد هر دو ضلع، زاویه داخلی میگویند. اندازه زاویه داخلی، معیار مهمی برای تقسیمبندی انواع چندضلعی است.
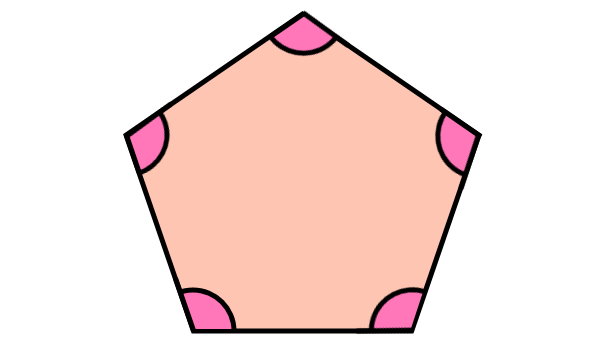
با توجه به اندازه زاویه داخلی، یک چندضلعی میتواند محدب، مقعر، منتظم یا غیرمنتظم باشد. یکی از نکات مشترک بین انواع چندضلعیها، فرمول مجموع زوایای داخلی آنها است.
فرمول مجموع زوایای داخلی چند ضلعی
مجموع زوایای داخلی هر چندضلعی، با استفاده از فرمول زیر به دست اندازه میآید:
- S: مجموع زوایای داخلی چندضلعی
- n: تعداد ضلعها
مثال ۳: محاسبه مجموع زوایای داخلی چند ضلعی
مجموع زوایای داخلی چندضلعی زیر چند است؟
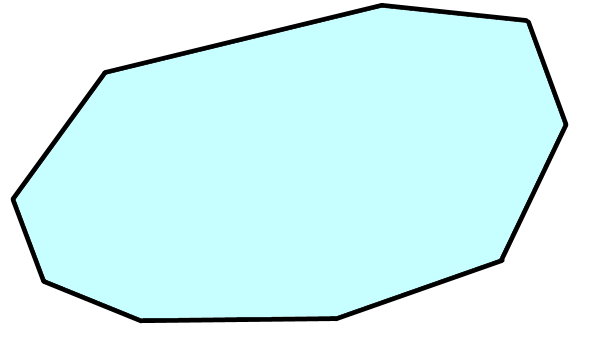
برای تعیین مجموع زوایای داخلی چندضلعیها، فقط به تعداد ضلعهای آنها نیاز داریم. تعداد ضلعهای چندضلعی بالا برابر با ۹ است. بنابراین، مجموع زوایای داخلی آن به صورت زیر محاسبه میشود:
- S: مجموع زوایای داخلی چندضلعی
- n: تعداد ضلعها برابر ۹
در نتیجه، مجموع زوایای داخلی یک چندضلعی با ۹ ضلع برابر با ۱۲۶۰ درجه است. به خاطر داشته باشید که شکل چندضلعی، بر روی مجموع زوایای داخلی آن تاثیری ندارد. در واقع، اگر مجموع زوایای داخلی هر نهضلعی را از شما بخواهند، جواب آن برابر با ۱۲۶۰ درجه خواهد بود.
اثبات فرمول مجموع زوایای داخلی چند ضلعی
هر چندضلعی را میتوان به صورت مجموعهای از مثلثهای به هم پیوسته نمایش داد. نمایش مثلثی یا اصطلاحا «مثلث بندی» (Triangulation)، با رسم قطرهای چندضلعی انجام میگیرد. به این ترتیب، جمع زوایای داخلی چندضلعی، با جمع زوایای داخلی مثلثها برابر خواهد بود. بخش اول فرمول مجموع زوایای داخلی (n-۲)، همان فرمول تعداد حداقل مثلث موجود در یک چندضلعی است.
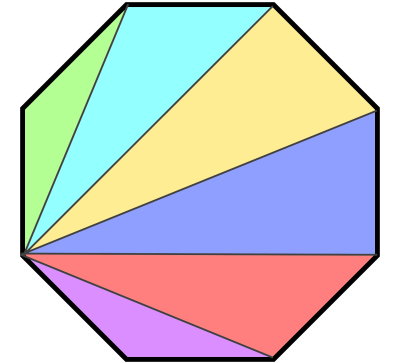
مجموع زوایای داخلی مثلث برابر با ۱۸۰ درجه میشود. بنابراین، مجموع زوایای داخلی چندضلعی، از ضرب تعداد مثلثهای درون آن در °۱۸۰ یا °۱۸۰ × (۲ - n) به دست میآید. در صورت تمایل به یادگیری بیشتر راجع به مجموع زوایای داخلی چندضلعیها و اثبات آنها، مطالعه مطلب «فرمول مجموع زوایای داخلی چندضلعی» را به شما پیشنهاد میکنیم.
فرمول زاویه داخلی چند ضلعی
برای تعیین اندازه یکی از زاویههای داخلی چندضلعی، به اندازه زاویههای دیگر یا مجموع آنها و تعداد ضلعها نیاز داریم. به طور کلی، زاویه داخلی چندضلعی از رابطه زیر به دست میآید:
مجموع زوایای داخلی دیگر - مجموع تمام زوایای داخلی = زاویه داخلی
در چندضلعیهای منتظم، فقط با دانستن تعداد ضلعها میتوانیم اندازه هر زاویه داخلی را به دست بیاوریم. به دلیل برابر بودن اندازه تمام زاویهها در این نوع چندضلعیها، فرمول زاویه داخلی آنها به صورت زیر نوشته میشود:
تعداد ضلعها ÷ مجموع زوایای داخلی = زاویه داخلی چندضلعی منتظم
عبارت جبری رابطه بالا برابر است با:
- α: زاویه داخلی
- n: تعداد ضلعهای چند ضلعی منتظم
مثال ۴: محاسبه زاویه داخلی چند ضلعی
یک چندضلعی دارای سه راس را در نظر بگیرید. اگر یکی اندازه یکی از راسهای این چندضلعی برابر با ۶۰ و اندازه زاویه داخلی راس دیگر آن برابر با ۳۰ درجه باشد، اندازه زاویه داخلی راس سوم چقدر خواهد بود؟
به منظور تعیین زاویه داخلی راس سوم، ابتدا باید مجموع زوایای داخلی را حساب کنیم. این اندازه با استفاده از فرمول زیر محاسبه میشود:
- S: مجموع زوایای داخلی چندضلعی
- n: تعداد ضلعها برابر ۳ (تعداد ضلعها و راسهای چندضلعی با هم برابرند.)
اندازه زاویه داخلی راس سوم برابر است با:
مجموع دو زاویه دیگر - مجموع سه زاویه = زاویه سوم
اندازههای معلوم را درون رابطه بالا قرار میدهیم:
(۳۰° +۶۰°) - ۱۸۰° = زاویه سوم
۹۰° - ۱۸۰° = زاویه سوم
۹۰° = زاویه سوم
در نتیجه، اندازه زاویه داخلی سوم برابر با ۹۰ درجه است.
مثال ۵: محاسبه زاویه داخلی چندضلعی منتظم
یک چندضلعی منتظم با هفت راس را در نظر بگیرید. اندازه هر زاویه داخلی این چندضلعی را حساب کنید.
تعداد راسهای یک چندضلعی، با تعداد ضلعهای آن برابر است. بنابراین، صورت مسئله، اندازه زاویه داخلی یک هفتضلعی منتظم را از ما میخواهد. به منظور به دست آوردن این اندازه، از فرمول زیر استفاده میکنیم:
- α: زاویه داخلی هفتضلعی منتظم
- n: تعداد ضلعها برابر با ۷
در نتیجه، هر یک از زوایای داخلی یک هفتضلعی منتظم برابر با ۱۲۸/۵۷ درجه است. به منظور آشنایی بیشتر با مباحث مرتبط با محاسبه زاویه داخلی چندضلعیها، مطالعه مطلب «فرمول بدست آوردن مجموع زوایای داخلی چندضلعی + حل تمرین» را به شما پیشنهاد میکنیم.
زاویه خارجی چند ضلعی چیست؟
امتداد ضلعهای یک چندضلعی را در نظر بگیرید. هر امتداد، با ضلع مجاورش، زاویهای را میسازد که به آن، زاویه خارجی میگویند. زوایای خارجی و داخلی چندضلعی، با یکدیگر زاویه ۱۸۰ درجه (زاویه نیمصفحه) میسازند. روابط بین هر زاویه خارجی با زاویه داخلی مجاور آن به صورت زیر نوشته میشوند:
۱۸۰° = زاویه خارجی + زاویه داخلی
زاویه خارجی - °۱۸۰ = زاویه داخلی
زاویه داخلی - °۱۸۰ = زاویه خارجی
مثال ۶: محاسبه زوایای خارجی از روی زوایای داخلی
اندازه زوایای خارجی چندضلعی معرفی شده در مثال ۴ را حساب کنید.
اندازه زوایای داخلی چندضلعی مثال ۴ برابر بودند با:
۶۰° = زاویه داخلی اول
۳۰° = زاویه داخلی دوم
۹۰° = زاویه داخلی سوم
بر اساس این اندازهها، زوایای خارجی برابر هستند با:
زاویه داخلی اول - °۱۸۰ = زاویه خارجی اول
۶۰° - ۱۸۰° = زاویه خارجی اول
۱۲۰° = زاویه خارجی اول
زاویه داخلی دوم - °۱۸۰ = زاویه خارجی دوم
۳۰° - ۱۸۰° = زاویه خارجی دوم
۱۵۰° = زاویه خارجی دوم
زاویه داخلی سوم - °۱۸۰ = زاویه خارجی سوم
۹۰° - ۱۸۰° = زاویه خارجی سوم
۹۰° = زاویه خارجی سوم
فرمول مجموع زوایای خارجی چند ضلعی
مجموع زوایای خارجی چندضلعی، هیچ فرمولی ندارد؛ چراکه این اندازه، همواره برابر ۳۶۰ درجه بوده و برای محاسبه آن نیازی به فرمول نیست. البته در چندضلعیهای منتظم، به دلیل برابر بودن تمام زوایای خارجی، فرمول زاویه خارجی به صورت زیر نوشته میشود:
- β: زاویه خارجی چندضلعی منتظم
- n: تعداد ضلعهای چند ضلعی منتظم
قطر چند ضلعی چیست؟
قلم خود را بر روی یکی از گوشههای چندضلعی قرار دهید.
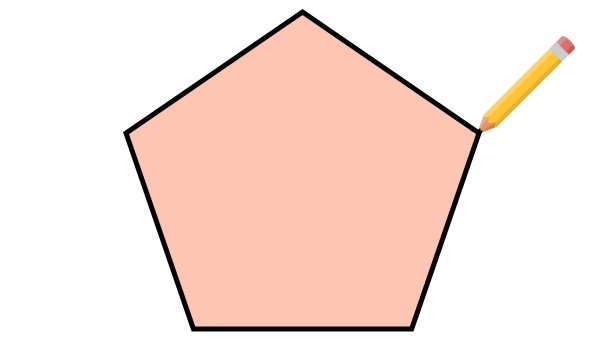
سپس، پارههخطی از آن گوشه به یک گوشه غیرمجاور رسم کنید. به این پارهخط، قطر میگویند.
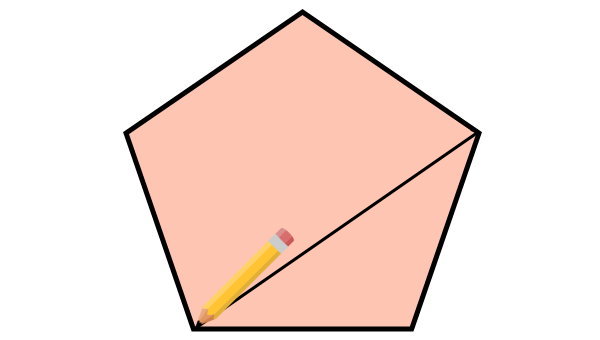
به غیر از مثلث (چندضلعی با سه ضلع)، تمام چندضلعیها دارای حداقل یک قطر هستند.
تعداد قطرهای چندضلعی با تعداد اضلاع آن رابطه مستقیم دارد. هر چه تعداد ضلعهای چندضلعی بیشتر باشد، تعداد قطرهای قابل رسم برای آن افزایش مییابد.
فرمول قطر چند ضلعی
تعداد قطرهای یک چندضلعی، از فرمول زیر به دست میآید:
- dn: تعداد قطرهای چندضلعی
- n: تعداد ضلعهای چندضلعی
این فرمول برای تمام انواع چندضلعی قابل استفاده است و نوع آنها بستگی ندارد.
مثال ۷: رسم قطرهای چند ضلعی
تصویر زیر، دو چندضلعی را نمایش میدهد. قطرهای این چندضلعیها را رسم کنید. هر شکل چند قطر دارد؟
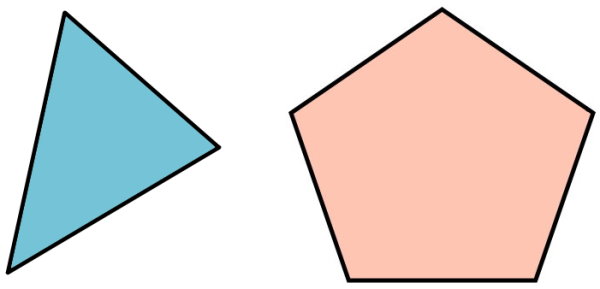
شکل سمت راست، دارای ۵ ضلع و ۵ راس است. به منظور رسم قطرهای این شکل، قلم خود را بر روی یکی از گوشههای آن قرار میدهیم و سپس، پارهخطی را به سمت گوشههای غیر مجاور رسم میکنیم. پارهخطهای رسمشده، قطرهای چندضلعی هستند. در مرحله بعد، به روی گوشههای دیگر میرویم و مرحله قبل را تکرار میکنیم. این کار را تا رسم تمام قطرها از روی تمام گوشهها ادامه میدهیم.
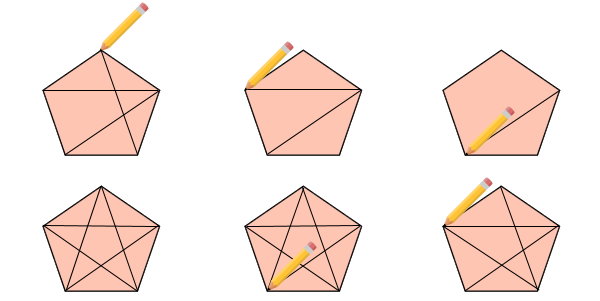
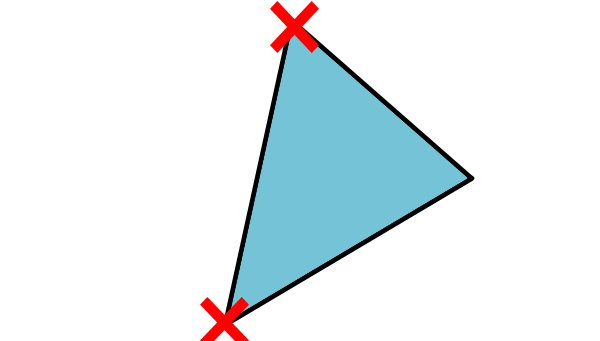
تعداد قطرهای چندضلعی دارای پنج ضلع را میشماریم. این چندضلعی، ۵ قطر دارد. شکل دیگر، از ۳ ضلع و ۳ راس تشکیل میشود. قلم خود را بر روی یکی از گوشهها قرار میهیم.

گوشه دوم و سوم، با این گوشه مجاور هستند. به غیر از این دو گوشه، گوشه دیگری وجود ندارد که بتوانیم به کمک آن، قطر چندضلعی را رسم کنیم. به همین دلیل، چندضلعی بالا (چندضلعی با سه ضلع)، هیچ قطری ندارد.
مثال ۸: محاسبه تعداد قطرهای چند ضلعی
تعداد قطرهای یک چند ضلعی با ۴ ضلع و یک چندضلعی با شش ضلع را محاسبه کنید.
تعداد قطرهای چندضلعی با استفاده از فرمول زیر محاسبه میشود:
- dn: تعداد قطرهای چندضلعی
- n: تعداد ضلعهای چندضلعی
برای یک چندضلعی با چهار ضلع داریم:
- d۴: تعداد قطرهای چندضلعی با چهار ضلع
- n: تعداد ضلعها برابر با ۴
برای یک چندضلعی با شش ضلع نیز داریم:
- d۶: تعداد قطرهای چندضلعی با شش ضلع
- n: تعداد ضلعها برابر با ۶
انواع چند ضلعی چه هستند ؟
چندضلعیها معمولا بر اساس معیارهای مختلفی نظیر مشخصات ضلعها و زاویهها تقسیمبندی میشود. انواع چندضلعی بر اساس این معیارها عبارتند از:
- انواع چند ضلعی بر اساس تعداد اضلاع
- انواع چند ضلعی بر اساس اندازه هر زاویه داخلی
- انواع چند ضلعی بر اساس اندازه تمام اضلاع
- متساوی الاضلاع
- مختلف الاضلاع
- انواع چند ضلعی بر اساس اندازه تمام زوایا
- منتظم
- غیرمنتظم
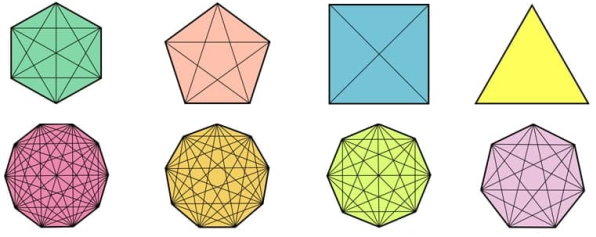
تصویر زیر، برخی از شناخته شدهترین انواع چندضلعیهای را نمایش میدهد.
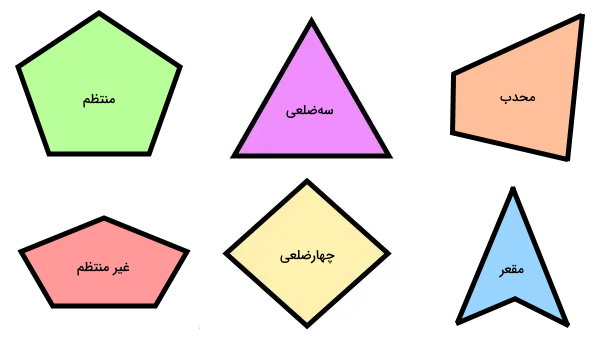
برخی از انواع چندضلعیها را میتوان به چندین نوع تقسیم کرد. در ادامه، به معرفی انواع چندضلعیها میپردازیم.
انواع چند ضلعی بر اساس تعداد ضلع
تعداد ضلع، اولین معیاری است که برای تقسیمبندی چندضلعیها به ذهن هر کسی میرسد. مطمئنا عنوان «چند» ضلعی نیز در این موضوع بیتاثیر نیست. بر اساس اینکه هر خط شکسته بسته چند ضلع دارد، یک نام برای آن در نظر گرفته میشود. جدول زیر، فهرستی از انواع چندضلعی را بر اساس تعداد ضلعهایشان نمایش میدهد. در کنار عنوان فارسی این چندضلعیها، اصطلاح مربوط به آنها نیز آورده شده است.
| تعداد ضلعها | نام فارسی چندضلعی | اصطلاح یونانی چندضلعی |
| ۳ | مثلث (سهضلعی) | تریگون |
| ۴ | چهارضلعی | تتراگون |
| ۵ | پنجضلعی | پنتاگون |
| ۶ | ششضلعی | هگزاگون |
| ۷ | هفتضلعی | هپتاگون |
| ۸ | هشتضلعی | اوکتاگون |
| ۹ | نهضلعی | نوناگون |
| ۱۰ | دهضلعی | دکاگون |
همانطور که مشاهده میکنید، هیچ چندضلعی با ۲ یا ۱ ضلع وجود ندارد. یک چندضلعی باید حداقل ۳ ضلع داشته باشد. در ادامه برخی از انواع شناختهشده چندضلعیهای بالا را به طور خلاصه معرفی میکنیم.
سه ضلعی و انواع سه ضلعی
«مثلث» (Triangle)، یکی از چندضلعیهای معروف و پرکاربرد است که به عنوان شکلهای پایهای هندسی در نظر گرفته میشود. از انواع مختلف مثلث میتوان به موارد زیر اشاره کرد:
- بر اساس ضلع
- متساوی الاضلاع (سه ضلع برابر)
- متساوی الساقین (دو ضلع برابر)
- مختلف الاضلاع (بدون ضلع برابر)
- بر اساس زاویه داخلی
- حاده (سه زاویه کوچکتر از ۹۰ درجه)
- قائمه (یک زاویه ۹۰ درجه)
- منفرجه (یک زاویه بزرگتر از ۹۰ درجه)
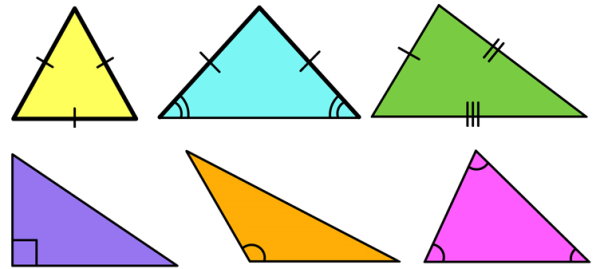
مباحث مربوط به مثلث و کاربردهای آن بسیار گسترده هستند. در صورت علاقه به یادگیری بیشتر و بهتر راجع به این چندضلعی، مطالعه مجموعه مطالب زیر را به شما پیشنهاد میکنیم:
چهارضلعی و انواع چهار ضلعی
«چهارضلعی» (Quadrilateral) نیز مانند مثلث، از چندضلعیهای پرکاربرد در هندسه به شمار میرود. شناخته شدهترین چهارضلعی، مربع است. این چندضلعی، از ۴ ضلع برابر و ۴ زاویه قائمه تشکیل میشود.
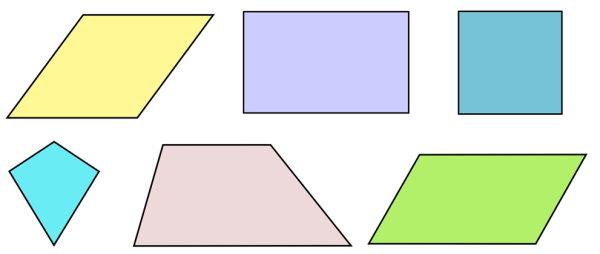
در تقسیمبندی چهارضلعیها، معمولا اندازه و موازی بودن ضلعها مورد نظر قرار میگیرد. انواع چهارضلعیها بر این اساس عبارت هستند از:
- مربع
- تمام ضلعها مساوی
- تمام زاویهها مساوی (قائمه)
- مستطیل
- ضلعهای روبهرویی مساوی
- تمام زاویهها مساوی (قائمه)
- لوزی
- تمام ضلعها مساوی
- زاویههای روبهرویی مساوی
- متوازی الاضلاع
- ضلعهای روبهرویی مساوی و موازی
- زاویههای روبهرویی مساوی
- ذوزنقه
- دو ضلع روبهرویی موازی و دو ضلع روبهرویی دیگر غیر موازی
- کایت یا شبه لوزی
- ضلعهای مجاور مساوی
- دو زاویه روبهرویی مساوی و دو زاویه روبهرویی دیگر متفاوت
در رابطه با چهارضلعیها نیز مطالب بسیار متنوعی در مجله فرادرس تهیه شده است. در صورت تمایل به یادگیری راجع به این مباحث، مطالعه عنوانهای زیر را به شما پیشنهاد میکنیم:
- مجموعه مطالب تعاریف مربع و محاسبات مربوط به آن
- مجموعه مطالب تعاریف مستطیل و محاسبات مربوط به آن
- مجموعه مطالب تعاریف متوازی الاضلاع و محاسبات مربوط به آن
- مجموعه مطالب تعاریف لوزی و محاسبات مربوط به آن
انواع پنج ضلعی، شش ضلعی و دیگر چندضلعیها
با افزایش تعداد ضلعها، تقسیمبندی چندضلعیها سادهتر و کلیتر میشود. به منظور تقسیمبندی چندضلعیهای دیگری نظیر پنجضلعی، ششضلعی و غیره، معیارهای دیگری مانند اندازه ضلعها و زاویههای داخلی مد نظر قرار میگیرند.
انواع چند ضلعی بر اساس اندازه ضلع و زاویه: چند ضلعی منتظم و غیرمنتظم
به چندضلعیهایی که دارای ضلعهای برابر و زاویههای هماندازه باشند، چندضلعی منتظم میگویند. مثلث متساویالاضلاع با سه ضلع برابر و سه زاویه ۶۰ درجه، یک سهضلعی منتظم محسوب میشود. مربع نیز یک چهارضلعی منتظم با چهار ضلع برابر و چهار زاویه ۹۰ درجه است.
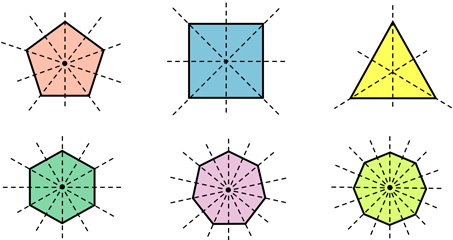
در صورت علاقه به یادگیری بیشتر راجع به چندضلعیهای منتظم، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
در طرف مقابل چندضلعی منتظم، چندضلعی غیرمنتظم قرار دارد. غیرمنتظم بودن یک چندضلعی، به معنای متفاوت بودن اندازه تمام ضلعها یا تمام زاویههای آن نیست. به عنوان مثال، لوزی، چهار ضلع با اندازههای برابر دارد. با این وجود، به دلیل برابر بودن اندازه زاویهها، این شکل به عنوان یک چندضلعی غیرمنتظم در نظر گرفته میشود.
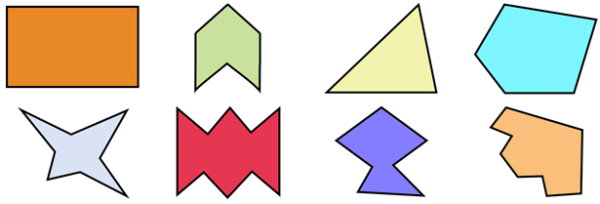
تصویر بالا، چند نمونه از چندضلعیهای غیرمنتظم را نمایش میدهد. در میان این چندضلعیها، یک مثلث و یک مستطیل نیز قابل مشاهده هستند. شکل برخی از چندضلعیهای بالا، یک تفاوت بزرگ با دیگر موارد دارد. اگر خوب به گوشههای تمام شکلها دقت کنید، متوجه خواهید شد که زاویه داخلی تعدادی از شکلها، بیشتر از ۱۸۰ درجه است. این ویژگی، یک معیار جدید جدید را برای تقسیمبندی چندضلعیها به وجود میآورد.
انواع چند ضلعی بر اساس اندازه زاویه داخلی
از دیگر معیارهای تقسیمبندی چندضلعیها، اندازه زاویه داخلی آنها است. بر این اساس، چندضلعیها به دو گروه اصلی زیر تقسیم میشوند:
- چندضلعی محدب یا کوژ
- چندضلعی مقعر یا کاو
شکل های چند ضلعی کوژ یا محدب
در «چند ضلعی محدب» (Convex Polygon)، تمام زاویههای کوچکتر از ۱۸۰ درجه هستند. مثلث، مربع، مستطیل، لوزی، ذوزنقه، متوازی الاضلاع، شبهلوزی و تمام چندضلعیهای منتظم، از مثالهای شناخته شده چندضلعیهای محدب در نظر گرفته میشوند. حداقل تعداد ضلعهای یک چندضلعی محدب برابر با ۳ (مثلث) است.
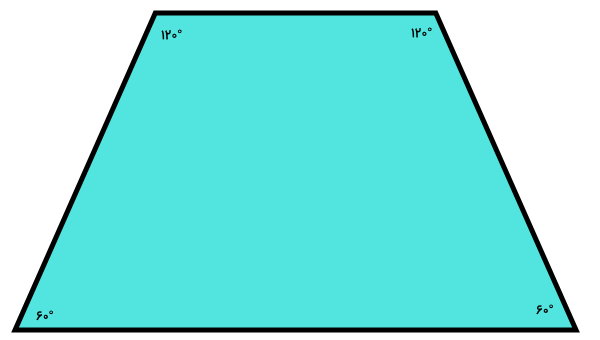
علاوه بر بررسی زاویههای داخلی، روشهای دیگری نیز برای تشخیص محدب یا غیرمحدب بودن چندضلعیها وجود دارد. به عنوان مثال، در چندضلعیهای محدب، تمام قطرهای چندضلعی محدب، درون آن قرار میگیرند. در صورت تمایل به یادگیری بیشتر راجع به چندضلعیهای محدب، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
- چندضلعی محدب چیست؟ — تعریف اجزا، ویژگیها و فرمولها
- مجموع زوایای داخلی چندضلعی محدب چیست؟ + حل مثال
- مجموع زوایای خارجی چندضلعی محدب چیست؟ + حل مثال
شکل های چند ضلعی کاو یا مقعر
در «چند ضلعی مقعر» (Concave Polygon)، حداقل یک زاویه بزرگتر از ۱۸۰ درجه وجود دارد. معروفترین چندضلعی مقعر، ستاره ساده است. اگر قطرهای یک چندضلعی ستارهای شکل را رسم کنید، حداقل یک قطر، خارج از شکل قرار میگیرد.

چندضلعی مقعر باید حداقل ۴ ضلع داشته باشد. اثبات این موضوع با استفاده از فرمول مجموع زوایای داخلی چندضلعیها انجام میگیرد. تصویر زیر، نمونههایی از یک چندضلعیهای مقعر را نمایش میدهد.
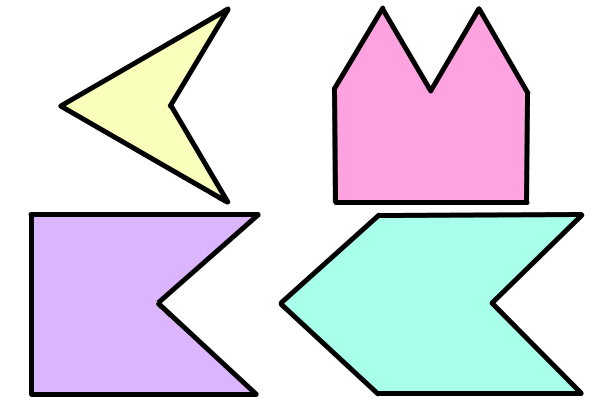
به منظور یادگیری بیشتر راجع به چندضلعیهای مقعر میتوانید به مطالعه مطالب زیر بپردازید:
- چندضلعی مقعر چیست؟ — تعریف اجزا، ویژگیها و فرمولها
- مجموع زوایای چندضلعی مقعر + حل تمرین و اثبات فرمول
انواع دیگر چند ضلعی ها
تقسیمبندی چندضلعیها به موارد معرفی شده در بخشهای قبلی محدود نمیشود. برخی دیگر از انواع چندضلعیها عبارت هستند از:
- چندضلعی ساده: به چندضلعی که هیچ یک از ضلعهای آن یکدیگر را قطع نمیکنند، چندضلعی ساده میگویند.
- چندضلعی متقاطع: اگر ضلعهای یک چندضلعی همدیگر را قطع کنند، آن چندضلعی، متقاطع است.
- چندضلعی راست خط: چندضلعی که تمام ضلعهای آن با ضلع مجاورشان زاویه قائمه میسازند، با عنوان چندضلعی راستخط شناخته میشود.
- چندضلعی ستارهای منتظم: به چندضلعیهایی که تمام ضلعها و زاویههای داخلی آن با هم برابر هستند و تمام ضلعها یکدیگر را قطع میکنند، چندضلعی ستارهای منتظم میگویند. چندضلعی ستارهای منتظم با چندضلعی ستارهای شکل مقعر تفاوت دارد.
- چندضلعی محاطی: اگر تمام راسهای یک چندضلعی، بر روی محیط یک دایره قرار داشته باشند، آن چند ضلعی، محاطی است.
- چندضلعی محیطی یا مماسی: اگر تمام ضلعهای یک چندضلعی بر دایرهای مماس باشند، آن چندضلعی، محیطی است.
- چندضلعی یکنوا: چندضلعی P، نسبت به خط L، یکنوا است، اگر هر تمام خطوط عمود بر خط L، چندضلعی P را حداکثر در دو نقطه قطع کنند.
محیط چند ضلعی چیست و چگونه بدست می آید؟
محیط چندضلعیها، اندازه دور این شکلهای هندسی است. محیط، از جمع اندازه ضلعها به دست میآید. بنابراین، اگر به عنوان مثال، یک سهضلعی داشته باشیم، اندازه محیط آن برابر خواهد بود با:
ضلع سوم + ضلع دوم + ضلع اول = محیط سهضلعی
بنابراین، برای محیط یک n ضلعی داریم:
ضلع n ام + .... + ضلع دوم + ضلع اول = محیط n ضلعی
به عبارت دیگر، مسافت طی شده بر روی ضلعهای چندضلعی، همان محیط چندضلعی است. در تصویر متحرک زیر، محیط چهارضلعی از رنگ سفید به سیاه تغییر میکند.

علاوه بر فرمول کلی، روشهای دیگری نیز برای محاسبه این محیط در انواع مختلف چندضلعیها وجود دارد. به عنوان مثال، در چندضلعیهای منتظم، اندازه تمام ضلعها با هم برابر هستند، بنابراین، محیط این چندضلعیها با توجه به فرمولهای جدول زیر محاسبه میشود.
| عنوان چندضلعی منتظم | فرمول محیط |
| مثلث متساوی الاضلاع | یک ضلع × ۳ |
| مربع | یک ضلع × ۴ |
| پنجضلعی منتظم | یک ضلع × ۵ |
| ششضلعی منتظم | یک ضلع × ۶ |
| هفتضلعی منتظم | یک ضلع × ۷ |
| هشتضلعی منتظم | یک ضلع × ۸ |
| نهضلعی منتظم | یک ضلع × ۹ |
| دهضلعی منتظم | یک ضلع × ۱۰ |
محیط چندضلعیهای خاص نظیر انواع مثلثها، مربع، مستطیل، لوزی و غیره، با استفاده از فرمولهای دیگر نیز به دست میآیند. در صورت تمایل به یادگیری نحوه محاسبه محیط چندضلعیها، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
- محیط سهضلعی
- محیط مربع
- محیط مستطیل
- محیط لوزی
- محیط متوازی الاضلاع
- محیط ذوزنقه
مساحت چند ضلعی چیست و چگونه بدست می آید؟
به اندازه محدوده درون ضلعهای یک چندضلعی، مساحت میگویند. محاسبه مساحت چندضلعی، پیچیدهتر از محاسبه محیط آن است. البته مساحت بسیاری از شکلهای متداول، فرمول سادهای دارد.
جدول زیر، فرمولهای مساحت برخی از چندضلعیهای محدب شناخته شده را نمایش میدهد.
| عنوان چندضلعی | فرمول مساحت چندضلعی |
| چندضلعی منتظم | ۲ ÷ (محیط × ارتفاع) |
| مثلث | ۲ ÷ (قاعده × ارتفاع) |
| لوزی | ۲ ÷ (قطر کوچک × قطر بزرگ) |
| ذوزنقه | ۲ ÷ (جمع قاعدهها × ارتفاع) |
| مربع | خودش × یک ضلع |
| مستطیل | عرض × طول |
| متوازی الاضلاع | قاعده × ارتفاع |
تعیین مساحت چندضلعیهای مقعر و چندضلعیهای پیچیده، معمولا با استفاده از روشهایی نظیر تقسیمبندی، مثلثبندی و غیره انجام میگیرد. برای کسب اطلاعات بیشتر و یادگیری بهتر نحوه محاسبه مساحت چندضلعیها، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
- مساحت سهضلعی
- مساحت مربع
- مساحت مستطیل
- مساحت لوزی
- مساحت متوازی الاضلاع
- مساحت ذوزنقه
- مساحت چندضلعی منتظم
حجم چند ضلعی منتظم چیست و چگونه به دست می آید؟
حجم، اندازه فضای اشغال شده توسط یک شکل سهبعدی است. چندضلعیها، شکلهای دوبعدی هستند. بنابراین، هیچ حجمی برای آنها تعریف نمیشود. البته اگر قاعدههای یک شکل سهبعدی، چندضلعی باشد، به منظور محاسبه حجم آن، باید از مساحت چندضلعی استفاده کرد. به عنوان مثال، فرمول حجم منشور قائم عبارت است از:
مساحت قاعده × ارتفاع = مساحت منشور قائم
تصویر زیر، یک منشور قائم با قاعده سهضلعی را نمایش میدهد.
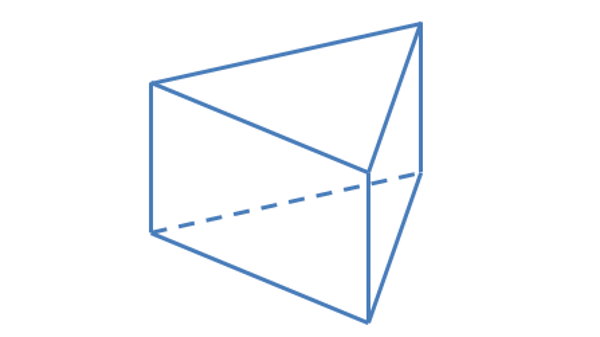
مساحت سهضلعی یا همان مثلث از رابطه زیر به دست میآید:
۲ ÷ (قاعده × ارتفاع) = مساحت مثلث
اگر اندازه مساحت مثلث را در ارتفاع منشور ضرب کنیم، حجم منشور محاسبه میشود.
تقارن در چند ضلعی ها چیست؟
در هندسه، شکلی را متقارن میگویند در هنگام اعمال تبدیلات هندسی (انتقال، چرخش یا انعکاس) بر روی آنها، تغییری در کلیت شکل رخ ندهد. انواع تقارن در چندضلعیها عبارت هستند از:
- تقارن محوری یا انعکاسی
- تقارن چرخشی
- تقارن مرکزی
تقارن محوری
تقارن محوری، یکی از شناخته شدهترین انواع تقارن شکلهای هندسی است. وجود تقارن محوری در یک چندضلعی، به دو شرط بستگی دارد:
- امکان یافتن خطی که شکل را به دو قسمت کاملا مساوی تقسیم کند.
- در صورت تا زدن چندضلعی بر روی آن خط (شرط ۱)، هر دو قسمت کاملا بر روی یکدیگر منطبق شوند.
بسیاری از چندضلعیها پرکاربرد در دنیای واقعی دارای تقارن محوری هستند. به عنوان مثال، مستطیل، یک چهارضلعی پرکاربرد با دو محور تقارن است. تصویر زیر، محورهای تقارن این چندضلعی را نمایش میدهد.
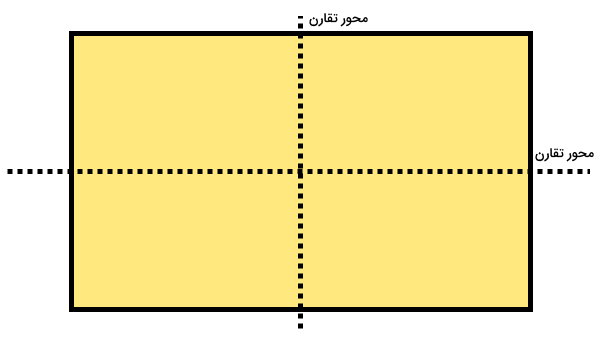
اگر مستطیل را در راستای یکی از محورهای تقارنش تا بزنیم، هر دو قسمت آن بر روی همدیگر قرار میگیرند. توجه داشته باشید که قطرهای مستطیل، آن را به قسمت مساوی تقسیم میکنند؛ اما در صورت تا زدن آن در راستای قطرها، شرط دوم تقارن محوری برقرار نمیشود. بنابراین، قطرهای مستطیل، محورهای تقارن آن نیستند. تصویر زیر، این نکته را به خوبی نمایش میدهد.
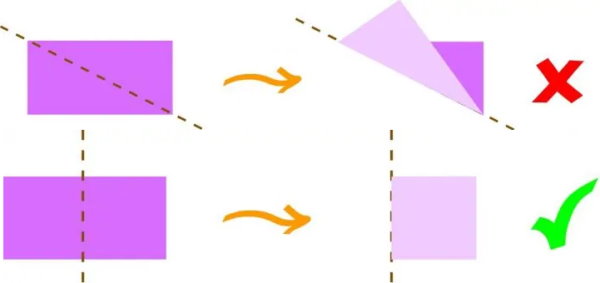
تقارن چرخشی در چند ضلعی
تقارن چرخشی در چندضلعیها، زمانی رخ میدهد که با دوران آنها حول یک نقطه، شکلشان هیچ تغییری نکند. تصویر متحرک زیر، این نوع تقارن را به خوبی نمایش میدهد.
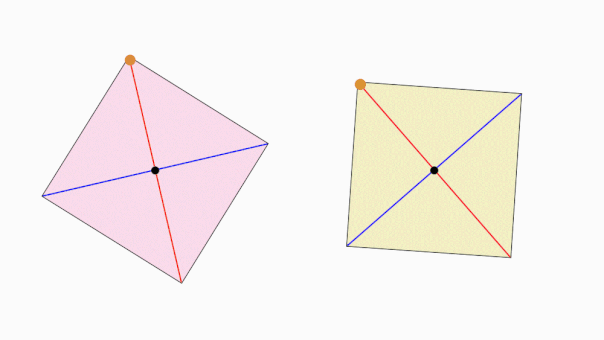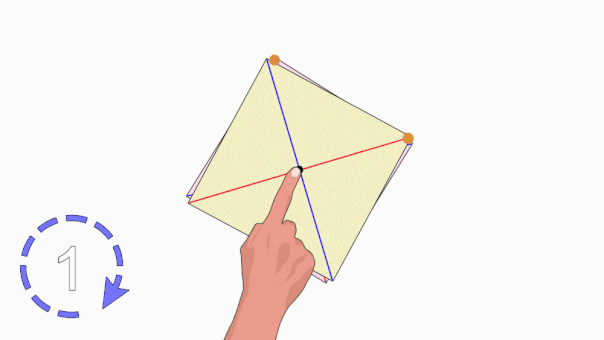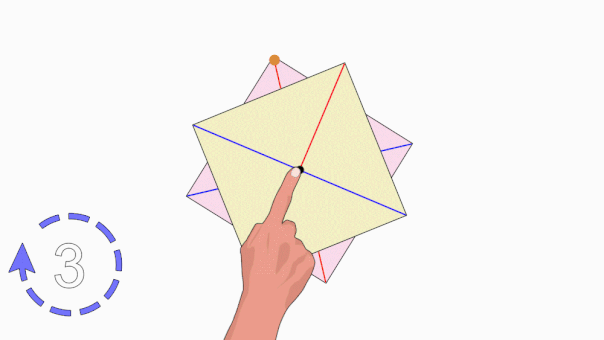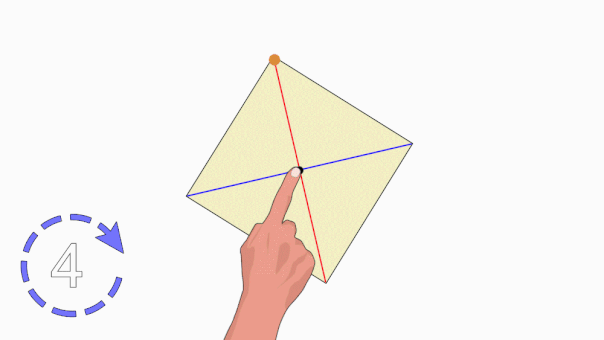
اگر یک مربع را حول مرکزش دوران دهیم، پس از هر چرخش ۹۰ درجهای، شکل مربع به حالت اولیه خود بازمیگردد. یک چرخش کامل، ۳۶۰ درجه است. در یک چرخش کامل مربع، چهار بار تقارن چرخشی رخ میدهد. بنابراین میگوئیم مرتبه تقارن چرخشی مربع برابر با ۴ است.
تقارن مرکزی در چند ضلعی
اگر فاصله دو نقطه مقابل بر روی محیط یک چندضلعی تا مرکز آن به یک اندازه باشد، میگوییم آن چندضلعی دارای تقارن مرکزی است. به عنوان مثال، چندضلعی مقعر زیر را در نظر بگیرید. نقاط A و B، بر روی محیط چندضلعی و دقیقا روبهروی هم قرار دارند.
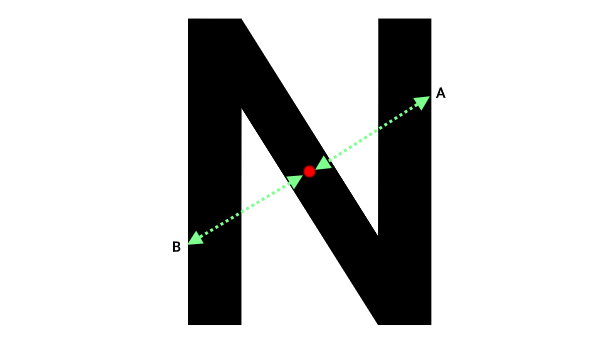
فاصله نقطه A تا مرکز نیز برابر با فاصله نقطه B تا مرکز است. بنابراین، این چندضلعی دارای تقارن مرکزی است. تقارن مرکزی، ارتباط نزدیکی با تقارن چرخشی دارد. اگر مرتبه تقارن یک چندضلعی برابر با عددی زوج باشد (بازگشتن به شکل اولیه پس از چرخش ۱۸۰ درجهای، ۹۰ درجهای و غیره)، آن شکل دارای تقارن مرکزی نیز خواهد بود.
تقارن در چند ضلعی منتظم
چندضلعیهای منتظم، شکلهای متقارن هستند. در صورت زوج بودن تعداد ضلعهای چندضلعی منتظم، هر سه نوع تقارن محوری، چرخشی و مرکزی در آنها وجود خواهد داشت. چندضلعیهای منتظم با ضلعهای فرد، تقارن مرکزی ندارند.
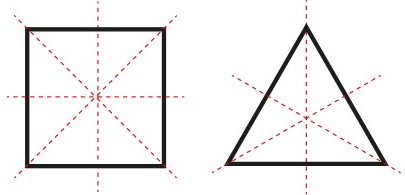
تعداد محورهای تقارن و مرتبه تقارن چرخشی یک چندضلعی منتظم، با تعداد ضلعهای آن برابری میکند. به عنوان مثال، مثلث متساوی الاضلاع (سهضلعی منتظم) دارای ۳ محور تقارن و مربع (چهارضلعی منتظم) دارای ۴ محور تقارن است. در حالت کلی داریم:
n = تعداد خط تقارن n ضلعی منتظم
n = مرتبه تقارن چرخشی n ضلعی منتظم
در n ضلعیهای منتظم، تمام عمود منصفهای اضلاع و تمام قطرها، محور تقارن محسوب میشوند. برای یادگیری بیشتر راجع به تقارن در چندضلعیهای منتظم، مطالعه مطلب «محور تقارن چندضلعی منتظم چیست؟ — به زبان ساده» را به شما پیشنهاد میکنیم.
رسم چند ضلعی چگونه انجام میشود؟
رسم چندضلعی، فرآیند نسبتا سادهای دارد. به منظور رسم یک چندضلعی دلخواه، ابتدا محل قرارگیری چند نقطه را درون صفحه کنید. این نقاط، بیانگر راسهای چندضلعی هستند.
بنابراین، اگر یک چندضلعی با تعداد ضلعهای مشخصی را مد نظر دارید، تعداد نقاط باید برابر با تعداد ضلعها باشد.

اکنون، دو نقطه مجاور را در نظر بگیرید. سپس، یک پارهخط بین این دو نقطه بکشید. این پارهخط، یکی از ضلعهای چندضلعی مورد نظر است.
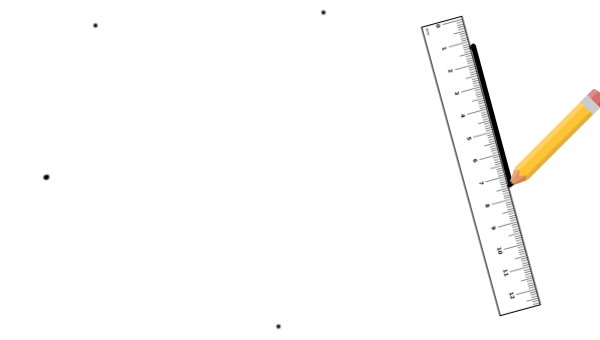
فرآیند بالا را برای تمام نقاط مجاور ادامه دهید تا شکل چندضلعی به دست بیاید.
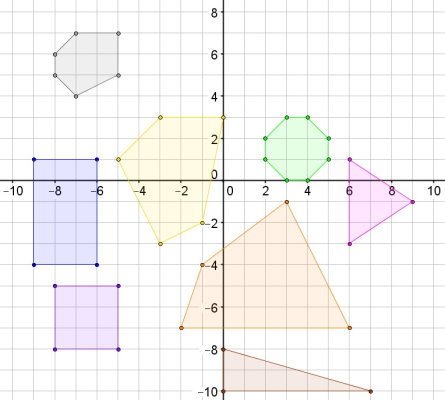
توجه داشته باشید که رسم دقیق یک چندضلعی، با استفاده از مختصات راسهای آن انجام میگیرد. اگر یک صفحه شطرنجی داشت باشید، میتوانید یک دستگاه مختصات در آن تشکیل دهید و مختصات هر راس را به راحتی مشخص کنید.
شکلهای چندضلعی، کاربرد بسیار گستردهای در مهندسی، معماری و هنر دارند. از اینرو، آشنایی با نحوه رسم چندضلعیها در نرمافزارهای تخصصی، از اهمیت بالایی برای طراحی در این حوزهها برخوردار است. به همین دلیل، در ادامه، نحوه رسم چندضلعیها در نرمافزارهای اتوکد و فتوشاپ را به طور خلاصه توضیح میدهیم.
رسم چند ضلعی در اتوکد
نرم افزار اتوکد، یکی از محبوبترین نرمافزارهای طراحی در حوزههای مهندسی عمران، مکانیک و معماری است. به منظور رسم چندضلعی در این نرمافزار، فقط باید مراحل زیر را طی کنید:
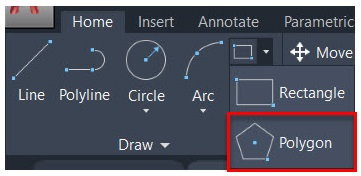
- کلیک بر روی زبانه «Home» در نوار ابزار اصلی نرمافزار
- کلیک بر روی آیکون «Polygon» در پنل «Draw» یا تایپ دستور «POLYGON» در خط فرمان و فشردن کلید «Enter»
- وارد کردن تعداد ضلعهای چندضلعی
- مشخص کردن مرکز چندضلعی یا گوشههای آن با استفاده از نشانگر و کلیک ماوس
- در صورت انتخاب مرکز (یکبار کلیک)، باید محاطی یا محیطی بودن چندضلعی را به همراه شعاع دایره مشخص کنید.
- در صورت انتخاب گوشه (چند بار کلیک)، باید به ترتیب و با توجه به تعداد ضلعها، بر روی نقاط مورد نظر (نقاط معرف راس) کلیک کنید.
رسم چند ضلعی در فتوشاپ
فتوشاپ، شناخته شدهترین نرمافزار ویرایش تصاویر است. به منظور دسترسی به ابزارهای رسم انواع چندضلعی در فتوشاپ، از نوار ابزار کناری، بر روی آیکون «Rectangle Tool» کلیک کنید.
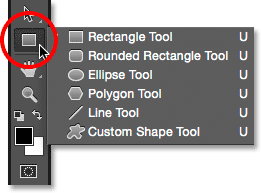
فتوشاپ، شش گزینه مختلف را برای رسم شکلهای هندسی در اختیار کاربر قرار میدهد. یکی از این گزینهها «Polygon Tools» است. با انتخاب این گزینه، امکان رسم چندضلعیها و تنظیم مشخصات اجزای آنها فراهم میشود.
سوالات متداول در رابطه با چند ضلعی
در این بخش، به برخی از سوالات پرتکرار در رابطه با چندضلعیها به طور خلاصه پاسخ میدهیم.
تعریف چند ضلعی در هندسه چیست ؟
چند ضلعی خط شکسته بسته است.
شرایط چند ضلعی بودن چیست؟
بسته بودن (اتصال نقطه انتهایی به ابتدایی) و مستقیم بودن اجزا (عدم وجود منحنی)، از شرایط یک چندضلعی هستند.
تفاوت چند ضلعی ها در چیست؟
تفاوت چندضلعیها در تعداد ضلع، اندازه زاویه داخلی (محدب، مقعر) و برابری اجز (منتظم و غیرمنتظم) است.
چگونه تعداد قطرهای یک چند ضلعی را حساب کنیم؟
تعداد قطرهای هر n ضلعی، از رابطه «۲ ÷ (۳ - n)n» حساب میشود.
چند ضلعی چند زاویه دارد ؟
چندضلعیها، به تعداد ضلعهایشان دارای زاویه داخلی، زاویه خارجی و زاویه مرکزی هستند.
چند ضلعی چند خط تقارن دارد ؟
هر n ضلعی میتواند بین ۰ تا n خط یا محور تقارن داشته باشد. n ضلعیهای منتظم، n محور تقارن دارند.
چند ضلعی که قطر ندارد چیست؟
مثلث. مثلث هیچ قطری ندارد.
فرق چند ضلعی محدب و مقعر چیست؟
تمام زاویههای داخلی چندضلعی محدب کوچکتر از ۱۸۰ درجه بوده؛ اما حداقل یکی از زاویههای داخلی چندضلعی مقعر، بزرگتر از ۱۸۰ درجه است.
چند ضلعی چند لبه دارد؟
لبه همان ضلع است. یک n ضلعی، n لبه دارد.
چند ضلعی که مرکز تقارن ندارد چیست ؟
بسیاری از چندضلعیها، میتوانند مرکز تقارن نداشته باشند. با این وجود، چندضلعیهای منتظم با تعداد ضلعهای فرد، شناخته شدهترین چندضلعیهای بدون مرکز تقارن هستند.
چهار ضلعی که خط تقارن ندارد اما دارای تقارن مرکزی است چه نام دارد؟
متوازی الاضلاع.
فرمول تعداد مثلث در چند ضلعی چیست ؟
فرمول تعداد مثلث در چند ضلعی برابر با «n - ۲» است.
آیا هر چند ضلعی منتظم محدب است ؟
بله. تمام چندچندضلعیهای منتظم، از نوع محدب (با زاویههای داخلی کوچکتر از ۱۸۰ درجه) هستند.
کوچکترین چند ضلعی چیست؟
کوچکترین چندضلعی، از نظر تعداد ضلعها، مثلث یا همان سهضلعی است.
حداقل اضلاع چند ضلعی چقدر است است؟
حداقل اضلاع چندضلعی محدب برابر با ۳ و حداقل اضلاع چندضلعی مقعر برابر با ۴ است.
چرا یک بیضی یا یک دایره چند ضلعی نیست؟
چون این شکلها از منحنی بسته تشکیل میشوند.
مربع چه نوع چند ضلعی است ؟
مربع، یک چهارضلعی منتظم است.
تشابه در چند ضلعی ها چیست؟
اگر تمام زوایای متناظر دو چندضلعی با یکدیگر برابر بوده و نسبت تمام ضلعهای متناظر آنها یکسان باشد، آن دو چندضلعی را متشابه میگویند.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش انواع چند ضلعی ها — تعاریف و تمامی فرمول های محیط و مساحت» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- چند ضلعی چیست ؟ — به زبان ساده(همین مطلب)
- چند ضلعی محدب چیست ؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده
- چند ضلعی مقعر چیست ؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده
- چند ضلعی منتظم چیست ؟ — به زبان ساده + فیلم آموزش رایگان و حل تمرین
- مجموع زوایای داخلی چند ضلعی محدب چیست ؟ — به زبان ساده + حل مثال
- مجموع زوایای خارجی چند ضلعی محدب چیست ؟ — به زبان ساده + حل مثال
- فرمول بدست آوردن مجموع زوایای داخلی چند ضلعی + حل تمرین
- مجموع زوایای چند ضلعی مقعر — به زبان ساده + حل تمرین و اثبات فرمول
- مجموع زوایای خارجی چند ضلعی منتظم — به زبان ساده + اثبات
- مساحت چند ضلعی منتظم چگونه بدست می آید ؟ — به زبان ساده + حل مثال
- محور تقارن چند ضلعی منتظم چیست ؟ — به زبان ساده













متاسفانه خواستهمن را برآورده نکرد.ولی چیزی از ارزش های شما کم نمیکنه
هر زاویه یک n ضلعی منتظم چند درجه هست؟
180° – (360°/n)
(۱۸۰ درجه منهای (تعداد اضلاع تقسیم بر ۳۶۰ درجه))
درسته؟
عالی
ممنون خیلی به من کمک کرد من برای کلاسم می خواستم تحقیق کنم که اومدم توی این سایت و دیدم خیلی مطالب مناسبی دارید.
دمتون گرم?
فرا درس عالیه تمام اموزشات در هر مورد
خداقوت????