فرادرسذوزنقه چیست؟ | تعاریف، انواع و محاسبات — به زبان ساده (+ فیلم آموزش رایگان)
در ادامه مجموعه آموزش‌های ریاضی مجله فرادرس، در این آموزش با ذوزنقه آشنا می‌شویم و روش محاسبه محیط و مساحت آن را بیان خواهیم کرد.
فیلم آموزشی آشنایی با ذوزنقه
تعریف ذوزنقه
ذوزنقه یک شکل هندسی دوبعدی است. این شکل هندسی 4 ضلع دارد که فقط دو ضلع آن موازی هستند. پس به طور ساده می‌توان برای تعریف ذوزنقه، چنین چیزی بیان کرد: ذوزنقه یک چهارضلعی است که فقط دو ضلع آن با هم موازی هستند.
در شکل زیر سه ذوزنقه مختلف نشان داده شده است. همان‌طور که مشاهده می‌کنید، در این سه شکل فقط دو ضلع موازی وجود دارد.
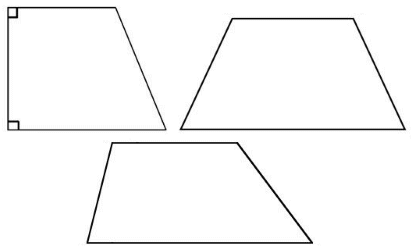
ذوزنقه یعنی چه؟
لغت‌نامه‌های مختلف ذوزنقه را به عنوان یک شکل هندسی معرفی کرده‌اند. به تعبیری، «ذوزنقه» (Trapezoid) از دو بخش «ذو» و «زنقه» تشکیل شده است.
«ذو» به معنای صاحب و دارنده است و «زنق» به معنی انحراف. بنابراین معنی تحت‌الفظی ذوزنقه «دارای انحراف» است و طبق آنچه در لغت‌نامه دهخدا نوشته شده، این واژه سابقه‌ای تاریخی دارد و دلیل آن هم این است که در این شکل هندسی فقط دو ضلع موازی هستند و دو ضلع دیگر انحراف دارند.
اصطلاحات مربوط به ذوزنقه
وقتی درباره ذوزنقه بحث می‌کنیم، با اصطلاحاتی مانند قاعده و ارتفاع و... روبه‌رو می‌شویم که بهتر است با آن‌ها آشنا شویم.
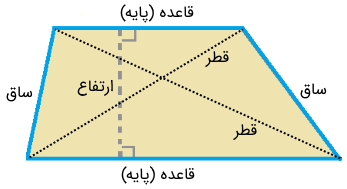
- قاعده: دو ضلع موازی ذوزنقه را پایه (قاعده) می‌نامند.
- ساق: هریک از دو ضلع غیرموازی ذوزنقه ساق نامیده می‌شوند.
- ارتفاع: کوتاه‌ترین فاصله بین دو قاعده ذوزنقه را ارتفاع می‌نامند. بنابراین، ارتفاع ذوزنقه بر قاعده‌های آن عمود است.
- قطر: قطر ذوزنقه پاره‌خطی است که دو رأس زوایای مقابل را به هم وصل می‌کند. هر ذوزنقه دو قطر دارد.
انواع ذوزنقه
با توجه به وضعیت ساق‌های ذوزنقه نسبت به یکدیگر و نسبت به قاعده‌ها، می‌توان آن‌ها را به چند نوع دسته‌بندی کرد: ذوزنقه متساوی الساقین، ذوزنقه قائم الزاویه و ذوزنقه مختلف الاضلاع.
ذوزنقه متساوی الساقین
همان‌گونه که از نامش مشخص است، ذوزنقه متساوی الساقین ذوزنقه‌ای است که دو ساق آن با هم برابر باشند. شکل زیر یک ذوزنقه متساوی الساقین را نشان می‌دهد که در آن، اندازه دو ساق AD و BC با هم برابر است.
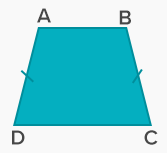
نکته: یک ویژگی ذوزنقه متساوی الساقین این است که زاویه‌ای که دو ساق با قاعده‌ها می‌سازند، با هم برابرند. این یعنی اینکه در شکل بالا، دو زاویه $$\angle ADC$$ و $$\angle BCD$$ با هم برابر هستند. همچنین، اندازه دو زاویه $$\angle DAB$$ و $$\angle ABC$$ یکسان است. عکس این مطلب نیز برقرار است. یعنی اگر زاویه‌هایی که نام بردیم، با هم برابر باشند، ذوزنقه متساوی الساقین است.
نکته: دو قطر ذوزنقه متساوی الساقین با هم برابرند. همچنین، اگر دو قطر ذوزنقه با هم برابر باشند، آن ذوزنقه متساوی الساقین است.
ذوزنقه قائم الزاویه
ذوزنقه قائم الزاویه نوعی ذوزنقه است که در آن، یکی از ساق‌ها بر قاعده‌ها عمود است. ذوزنقه شکل زیر قائم الزاویه است. همان‌طور که می‌بینیم، ساق AD بر دو قاعده AB و CD عمود است.
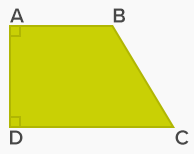
نکته: دقت کنید که فقط یکی از ساق‌ها بر قاعده‌ها عمود است، زیرا اگر هر دو ساق بر قاعده‌ها عمود باشند، دیگر آن شکل ذوزنقه نیست و یک مستطیل است.
ذوزنقه مختلف الاضلاع
در این نوع ذوزنقه هیچکدام از زاویه‌های داخلی و همچنین اضلاع با هم برابر نیستند. شکل زیر یک ذوزنقه مختلف الاضلاع را نشان می‌دهد که چهار زاویه آن متفاوت هستند.
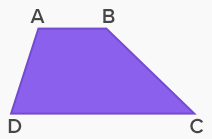
نکته: دقت کنید که گفتیم چهار زاویه نیز باید برابر نباشند، زیرا ممکن است اندازه چهار ضلع تفاوت داشته باشند، اما ذوزنقه قائم الزاویه باشد.
محیط ذوزنقه
همان‌طور که می‌دانیم، محیط یک شکل همان اندازه پیرامون یا دور آن شکل است. با توجه به این تعریف، محیط ذوزنقه نیز به راحتی برابر با مجموع اندازه هر چهار ضلع آن است. بنابراین، اگر بخواهیم محیط یک ذوزنقه (هر نوعی که باشد) را به دست آوریم، کافی است اندازه هر چهار ضلع آن را با هم جمع کنیم.
ذوزنقه شکل زیر را با اندازه اضلاع a و b و c و d در نظر بگیرید.
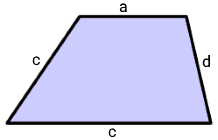
در این ذوزنقه، محیط به سادگی برابر است با:
$$a+b+c+d$$ = محیط ذوزنقه
برای آشنایی بیشتر محاسبه محیط ذوزنقه و مثال‌های آن، به مطلب «محیط ذوزنقه و محاسبه آن | به زبان ساده (+ فیلم آموزش رایگان)» در این لینک مراجعه کنید.
مساحت ذوزنقه
مساحت ذوزنقه برابر با نصفِ مجموع دو قاعده ضرب در ارتفاع است (یعنی (ارتفاع)*(نصف مجموع دو قاعده)).
این فرمول را به صورت ریاضی بیان می‌کنیم. ذوزنقه شکل زیر را در نظر بگیرید.
در ذوزنقه شکل بالا، اندازه قاعده‌ها a و b است و h نیز ارتفاع را نشان می‌دهد. در نتیجه، مساحت ذوزنقه برابر خواهد بود با:
$$ \frac 12 \times h \times (a + b) $$ = مساحت ذوزنقه
نکته: گاهی ممکن است اندازه ساق‌ها و قاعده‌ها را بدهند و از ما مساحت را بخواهند. در این موارد باید اندازه ارتفاع را از روی اطلاعات موجود محاسبه کنیم. برای آشنایی بیشتر با این موضوع، به آموزش «محاسبه مساحت ذوزنقه — به زبان ساده» در این لینک مراجعه کنید.
میانه مرکزی ذوزنقه
میانه مرکزی يک ذوزنقه، پاره‌خطی است که وسط دو ساق را به هم متصل می‌کند و اندازه آن برابر با میانگین طول قاعده‌های ذوزنقه است. در ذوزنقه شکل زیر، m اندازه میانه مرکزی را نشان می‌دهد و اندازه آن $$m=\frac{a+b}{2}$$ است.
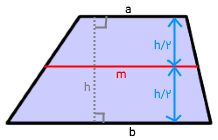
با داشتن مقدار میانه، می‌توانیم مساحت ذوزنقه را از فرمول زیر محاسبه کنیم:
$$m \times h$$ = مساحت ذوزنقه
مثال های ذوزنقه
در این بخش، چند مثال ساده را درباره ذوزنقه حل می‌کنیم.
مثال اول ذوزنقه
محیط و مساحت ذوزنقه زیر را به دست آورید.
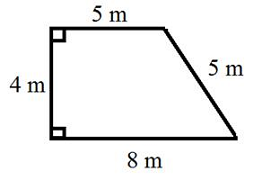
حل: همان‌طور که گفتیم، برای محاسبه محیط ذوزنقه کافی است اندازه چهار ضلع را با هم جمع کنیم. بنابراین، محیط ذوزنقه شکل بالا به صورت زیر محاسبه می‌شود.
$$ \large 5 \, \text{m}+ 4 \, \text{m} + 8 \, \text{m} + 5 \, \text{m} = 22 \, \text{m} $$ = محیط
بنابراین، محیط این ذوزنقه برابر با ۲۲ متر است (در اینجا حرف m به معنای متر است).
برای محاسبه مساحت، باید اندازه دو قاعده و ارتفاع را داشته باشیم. همان‌طور که می‌بینیم، اندازه دو قاعده ۵ و ۸ است. همچنین، با توجه به اینکه ذوزنقه قائم الزاویه است، ساق سمت چپ قائم آن همان ارتفاع بوده و اندازه آن ۴ است. در نتیجه، مساحت به صورت زیر به دست می‌آید:
$$\frac 12 \times (5+8)\times 4 = 26\; \text{m}^ 2 $$ = مساحت
مثال دوم ذوزنقه
نوع ذوزنقه‌های زیر را تعیین کنید.
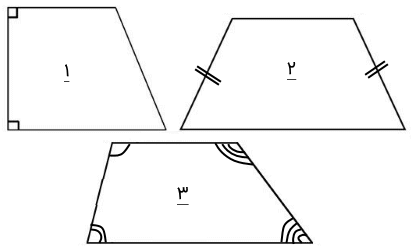
حل: نوع ذوزنقه ۱ با توجه به اینکه ساق سمت چپش بر دو قاعده عمود است، قائم الزاویه است. در ذوزنقه ۲، دو ساق برابر نشان داده شده‌اند و به همین دلیل این ذوزنقه متساوی الساقین است. در ذوزنقه ۳، همان‌طور که می‌بینیم، چهار زاویه متفاوت هستند و به همین دلیل، ذوزنقه مختلف الاضلاع است.
اگر یک خط دو ساق را قطع کند به شرط اینکه با دو قائده موازی باشد، حتما نسبت ارتفاع ذوزنقه ی بالایی به ارتفاع پایینی و نسبت قسمت ساق بالایی چپی به پایینی چپی و ساق بالایی راستی به پایینی راستی با هم برابر است؟
سلام ببخشید من داخل اثبات اینکه در هر ذوزنقه محل تلاقی قطرها و وسط های دو قاعده روی یک امتداد قرار دارند گیر افتادم میشه توضیح بدین
سلام؛ با معلوم بودن طول چهار ضلع ذوزنقه چجوری میشه رسمش کرد؟( به جز از روش مسئله رو حل شده فرض کنیم.)
سلام اگر اندازه های پایه های ذوزنقه رو بدن میتونیم اندازه هر پاره خطی بین پایه های ذوزنقه وموازی با با اون رو محاسبه کنیم
طول قطر های ذوزنقه رو چه جوری باید به دست آورد؟
سلام.
ذوزنقه زیر را با اضلاع و زاویه‌های معلوم در نظر بگیرید.
با استفاده از فرمول‌های زیر دو قطر $$d_1$$ و $$d_2$$ به دست می‌آیند:
$$d_1=\sqrt{a^2+d^2-2ad\cos \beta}\\ d_2=\sqrt{a^2+c^2-2ac\cos \alpha}$$
اگر زاویه‌های معلوم نباشند، می‌توانید از دو فرمول زیر استفاده کنید:
$$d_1=\sqrt{d^2+ab-\frac{a(d^2-c^2)}{a-b}}\\ d_2=\sqrt{c^2+ab-\frac{a(c^2-d^2)}{a-b}}$$
از اینکه با مجله فرادرس همراه هستید، خوشحالیم.
سلام اگر a داده باشند و b داده باشند h چه طوری بدست میاد
سلام.
با داشتن تنها $$a$$ و $$b$$ (پایه‌های ذوزنقه)، نمی‌توان $$h$$ (ارتفاع) آن را تعیین کرد. کافی است دو پایه را رسم کنید، خواهید دید که می‌توانید ارتفاع‌های مختلفی نیز رسم کنید.
از اینکه با مجله فرادرس همراه هستید، خوشحالیم.
بیست عالی توضیح دادین
عالی بود مشکل من رفع شد
خیلی بد
ارتفاع چی