فرادرس
مجموع زوایای خارجی چند ضلعی منتظم — به زبان ساده + اثبات
مجموع زوایای خارجی چند ضلعی منتظم برابر با ۳۶۰ درجه است. در این مقاله، به آموزش نحوه محاسبه زاویه خارجی و مجموع زوایای خارجی چند ضلعی منتظم به همراه حل چند مثال می‌پردازیم. در انتها، دلیل ثابت بودن حاصل‌جمع زاویه‌های خارجی چندضلعی‌های منتظم را اثبات می‌کنیم.
چند ضلعی منتظم چیست و چه اجزایی دارد؟
اگر در یک چندضلعی، طول تمام ضلع‌ها با هم و اندازه تمام زاویه‌ها با هم برابر باشند، به آن چندضلعی، چندضلعی منتظم می‌گویند.
مثلث متساوی الاضلاع و مربع، دو مورد از شناخته شده‌ترین چندضلعی‌های منتظم هستند.
از مهم‌ترین اجزای چندضلعی‌های منتظم می‌توان به ضلع، راس، زاویه داخلی و زاویه خارجی اشاره کرد. ارتفاع و شعاع از اجزای مورد استفاده در محاسبه مساحت چند ضلعی منتظم هستند. تمام اجزای چند ضلعی منتظم، اندازه‌های برابر دارند.
زاویه خارجی چند ضلعی منتظم چیست؟
به زاویه بین امتداد یک ضلع با ضلع مجاور آن در چندضلعی منتظم، زاویه خارجی می‌گویند. جمع زاویه داخلی و خارجی یک راس از چندضلعی منتظم، برابر با ۱۸۰ درجه می‌شود. به عبارت دیگر، زوایای داخلی و خارجی مجاور، مکمل یکدیگر هستند. تعداد زاویه‌های خارجی هر چندضلعی منتظم، برابر با تعداد ضلع‌های آن است.
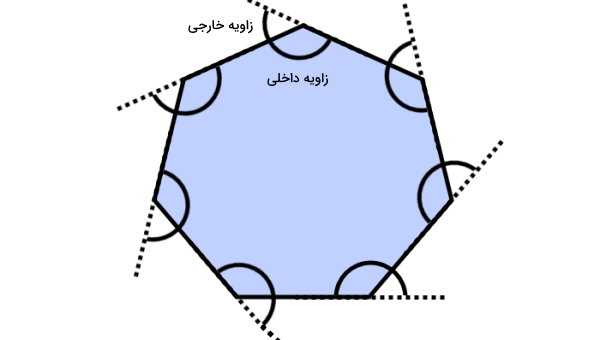
مجموع زوایای خارجی چند ضلعی منتظم چگونه بدست می آید ؟
مجموع زوایای خارجی چند ضلعی منتظم، ۳۶۰ درجه است. تعداد ضلع‌های چندضلعی منتظم، هیچ تاثیری بر روی مجموع زوایای خارجی آن ندارد.
به عبارت دیگر، اگر تمام زاویه‌های خارجی یک n ضلعی منتظم را با هم جمع کنیم، به عدد ۳۶۰ درجه می‌رسیم.
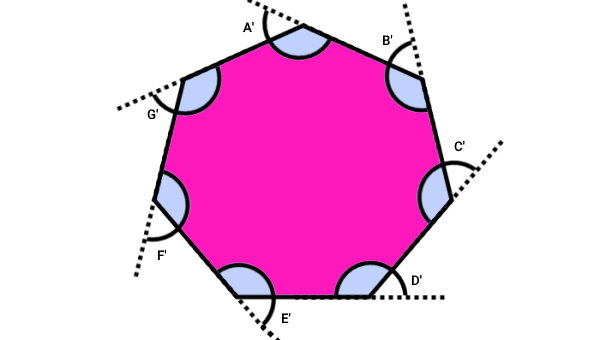
به عنوان مثال، برای هفت‌ضلعی منتظم بالا داریم:
$$
A' + B' + C' + D' + E' + F' + G' = ۳۶۰ ^ { \circ }
$$
مثال ۱: تعیین زاویه خارجی چندضلعی منتظم
مجموع سه زاویه خارجی یک چهارضلعی منتظم برابر با ۲۷۰ درجه است. اندازه زاویه چهارم این چهارضلعی را حساب کنید.
برای محاسبه زاویه چهارم چهارضلعی منتظم، چند روش وجود دارد. مجموع زوایای خارجی چند ضلعی منتظم برابر با ۳۶۰ درجه است. بنابراین، داریم:
زاویه خارجی ۴ + زاویه خارجی ۳ + زاویه خارجی ۲ + زاویه خارجی ۱ = مجموع زوایای خارجی
مجموع سه زاویه خارجی برابر با ۲۷۰ درجه است:
زاویه خارجی ۴ + °۲۶۰ = °۳۶۰
۲۷۰° - ۳۶۰° = زاویه خارجی ۴
۹۰° = زاویه خارجی ۴
اندازه زاویه خارجی چهارم چهارضلعی منتظم برابر با ۹۰ درجه است. در هر چندضلعی منتظم، تمام زاویه‌های خارجی برابر هستند. بنابراین، اگر مجموع سه زاویه خارجی را بر تعداد آن‌ها تقسیم کنیم، اندازه هر زاویه و همچنین اندازه زاویه خارجی چهارم به دست می‌آید:
تعداد زوایا ÷ مجموع زوایا = اندازه هر زاویه خارجی
۳ ÷ ۲۷۰° = اندازه هر زاویه خارجی
۹۰° = اندازه هر زاویه خارجی
البته روش دیگری نیز برای محاسبه مستقیم هر یک از زاویه‌های خارجی چندضلعی منتظم وجود که در ادامه به توضیح آن می‌پردازیم.
فرمول زاویه خارجی چند ضلعی منتظم چیست ؟
هر یک از زاویه‌های خارجی چند ضلعی منتظم، از تقسیم عدد ۳۶۰ بر تعداد ضلع‌ها به دست می‌آید:
$$
\beta = \frac { ۳۶۰^ {\circ} } { n }
$$
- β: زاویه خارجی چندضلعی منتظم
- n: تعداد ضلع‌های چندضلعی منتظم
مثال ۲: تعیین نوع چندضلعی
اندازه تمام زاویه‌های خارجی یک چندضلعی برابر با ۷۲ درجه است. به چندضلعی چه می‌گویند؟
اندازه یک زاویه داخلی این چندضلعی از رابطه زیر به دست می‌آید:
۱۸۰° = زاویه خارجی + زاویه داخلی
زاویه خارجی - °۱۸۰ = زاویه داخلی
۷۲° - ۱۸۰° = زاویه داخلی
۱۰۸° = زاویه داخلی
یکی از زاویه‌های داخلی چندضلعی منتظم برابر با ۱۰۸ درجه است. به دلیل برابر بودن تمام زاویه‌های خارجی، تمام زاویه‌های داخلی آن نیز برابر با ۱۰۸ درجه خواهند بود. در نتیجه، این چندضلعی، یک چندضلعی محدب است. به چندضلعی محدب با زاویه‌های داخلی برابر، چندضلعی منتظم می‌گویند. تعداد ضلع‌های این چندضلعی منتظم توسط رابطه زیر محاسبه می‌شود:
$$
\beta = \frac { ۳۶۰^ {\circ} } { n }
$$
- β: زاویه خارجی چندضلعی منتظم برابر با ۷۲
- n: تعداد ضلع‌های چندضلعی منتظم
$$
۷۲^ {\circ} = \frac { ۳۶۰^ {\circ} } { n }
$$
$$
n = \frac { ۳۶۰^ {\circ} } { ۷۲^ {\circ} }
$$
$$
n = ۵
$$
تعداد ضلع‌های چندضلعی منتظم برابر با ۵ است. به این چندضلعی، یک پنج‌ضلعی محدب منتظم می‌گویند.
اثبات مجموع زوایای خارجی چند ضلعی منتظم
به منظور اثبات مجموع زوایای خارجی چند ضلعی منتظم، ابتدا باید با فرمول محاسبه مجموع زوایای داخلی چندضلعی منتظم آشنا شوید.
این فرمول به صورت زیر نوشته می‌شود:
$$
S = ( n - ۲ ) \times ۱۸۰°
$$
- S: مجموع زوایای داخلی چند ضلعی منتظم
- n: تعداد ضلع‌های چندضلعی منتظم
برای آشنایی با نحوه اثبات این فرمول، مطالعه مطلب «فرمول بدست آوردن مجموع زوایای داخلی چند ضلعی + حل تمرین» را به شما پیشنهاد می‌کنیم. در بخش‌های قبل، اشاره کردیم که مجموع هر زاویه داخلی با زاویه خارجی مجاورش، برابر با ۱۸۰ درجه است:
$$
\alpha + \beta = ۱۸۰ ^ { \circ }
$$
هر چندضلعی منتظم، به اندازه تعداد ضلع‌هایش (n)، زاویه داخلی و خارجی دارد. جمع تمام زاویه‌های داخلی و خارجی یک n ضلعی عبارت است از:
$$
۱۸۰ ^ { \circ } n
$$
به عبارت دیگر، مجموع زوایای خارجی ('S) با مجموع زوایای داخلی (S) از رابطه زیر به دست می‌آید:
$$
S + S' = ۱۸۰ ^ { \circ } n
$$
فرمول مجموع زوایای داخلی (S) را در رابطه بالا قرار می‌دهیم:
$$
( n - ۲ ) \times ۱۸۰° + S' = ۱۸۰ ^ { \circ } n
$$
$$
S' = ۱۸۰ ^ { \circ } n - ( n - ۲ ) \times ۱۸۰°
$$
$$
S' = ۱۸۰ ^ { \circ } n - ۱۸۰ ^ { \circ }n + ۳۶۰ ^ { \circ }
$$
$$
S' = ۳۶۰ ^ { \circ }
$$
در نتیجه، مجموع زوایای خارجی یک n ضلعی منتظم، همواره برابر با ۳۶۰ درجه است و به مقدار n بستگی ندارد.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش انواع چند ضلعی ها — تعاریف و تمامی فرمول های محیط و مساحت» است. در ادامه، می‌توانید فهرست این مطالب را ببینید:
- چند ضلعی چیست؟ — به زبان ساده
- چند ضلعی محدب چیست؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده
- چند ضلعی مقعر چیست؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده
- چند ضلعی منتظم چیست؟ — به زبان ساده + فیلم آموزش رایگان و حل تمرین
- مجموع زوایای داخلی چند ضلعی محدب چیست؟ — به زبان ساده + حل مثال
- مجموع زوایای خارجی چند ضلعی محدب چیست؟ — به زبان ساده + حل مثال
- فرمول بدست آوردن مجموع زوایای داخلی چند ضلعی + حل تمرین
- مجموع زوایای چند ضلعی مقعر — به زبان ساده + حل تمرین و اثبات فرمول
- مجموع زوایای خارجی چند ضلعی منتظم — به زبان ساده + اثبات(همین مطلب)
- مساحت چند ضلعی منتظم چگونه بدست می آید؟ — به زبان ساده + حل مثال
- محور تقارن چند ضلعی منتظم چیست؟ — به زبان ساده
