چند ضلعی محدب چیست؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده

چند ضلعی محدب خط بستهای است که از راسهایی با زاویه کوچکتر از ۱۸۰ درجه تشکیل میشود. اگر حتی یکی از زاویههای یک چندضلعی، بزرگتر از ۱۸۰ درجه باشد، نمیتوان آن را محدب در نظر گرفت. در این آموزش، ابتدا تعاریف چند ضلعی محدب و روشهای تشخیص آن را مورد بررسی قرار میدهیم. سپس، ضمن معرفی فرمولهای محاسبه مجموع زاویهها (داخلی و خارجی)، اجزا و ویژگیهای این نوع چندضلعی، به حل چندین مثال متنوع میپردازیم.
چند ضلعی چیست؟
چندضلعی، یک خط شکسته بسته است که اضلاع آن یکدیگر را فقط در راسها قطع میکنند.
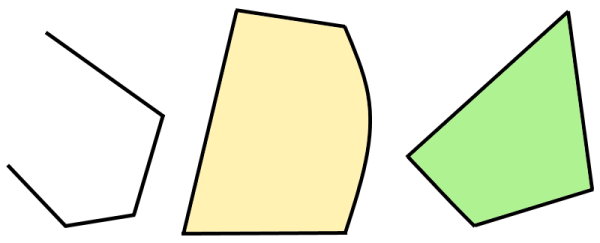
تصویر زیر، تفاوت بین یک چندضلعی با شکلهای دیگر را نمایش میدهد. به دلیل وجود یک منحنی در شکل وسط و بسته نبودن شکل سمت چپ، این شکلها به عنوان چندضلعی در نظر گرفته نمیشوند.
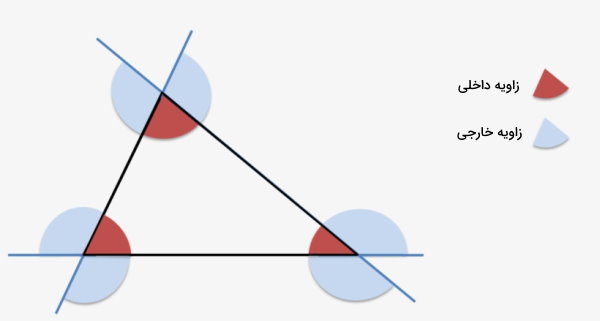
زاویه، یکی از مهمترین اجزای چندضلعیها است که به منظور تشخیص نوع آنها مورد استفاده قرار میگیرد. زاویه، از دو ضلع و یک راس تشکیل میشود. تعداد زاویههای داخلی و خارجی هر چندضلعی، برابر با تعداد ضلعهای آن است.
انواع چند ضلعی چه هستند؟
چندضلعیها بر اساس معیارهای مختلف به انواع زیر تقسیم میشوند:
- بر اساس برابری طول ضلعها و زاویهها
- منتظم
- غیر منتظم
- بر اساس اندازه زاویه داخلی راسها
- محدب
- مقعر
- بر اساس تعداد ضلع
چند ضلعی محدب چیست؟
به چندضلعیهایی که هیچیک از راسهای آن، زاویه بزرگتر از ۱۸۰ درجه ندارند، چند ضلعی محدب میگویند. چندضلعیهای محدب با عنوان چندضلعیهای کوژ نیز شناخته میشوند.
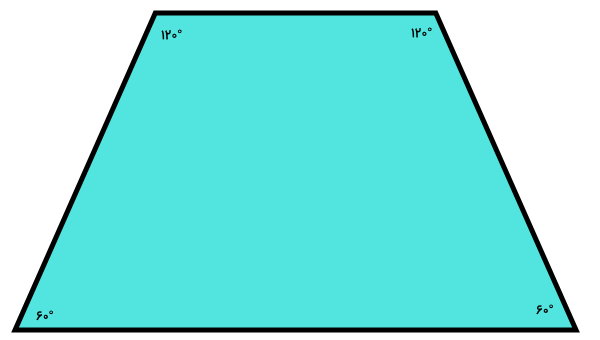
تصویر زیر، نمونهای از یک چهارضلعی محدب به نام ذوزنقه را نمایش میدهد. هیچیک از زاویههای داخلی ذوزنقه، بزرگتر از ۱۸۰ درجه نیستند.
چند نمونه چند ضلعی محدب
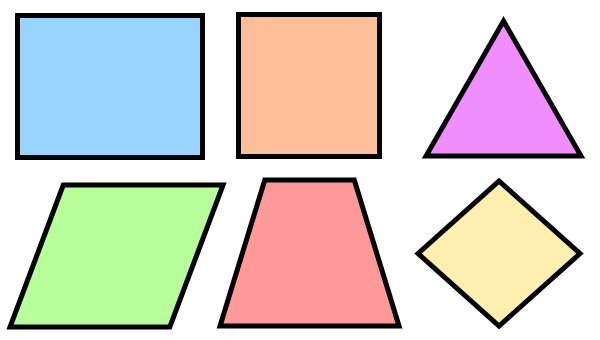
مثلث، مربع، مستطیل، لوزی، ذوزنقه و متوازیالاضلاع، از شناخته شدهترین مثالهای چندضلعی محدب هستند. علاوه بر این موارد، تمام چندضلعیهای منتظم نیز به عنوان چندضلعیهای محدب در نظر گرفته میشوند.
سه روش تشخیص چند ضلعی محدب
تشخیص محدب بودن یا نبودن چندضلعیها، معمولا توسط یکی از روشهای زیر انجام میگیرد:
- تعیین نوع زاویههای داخلی چندضلعی
- ترسیم امتداد ضلعهای چندضلعی
- اتصال دو نقطه درون محیط چندضلعی به یکدیگر
تشخیص چندضلعی محدب با استفاده از زاویههای داخلی
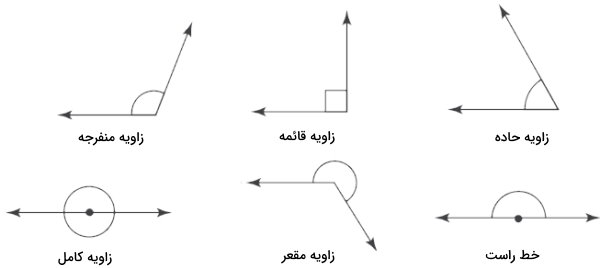
زاویههای یک چند ضلعی میتوانند کوچکتر از ۹۰ درجه (حاده)، مساوی با ۹۰ درجه (قائمه)، بزرگتر از ۹۰ درجه (منفرجه) یا بزرگتر از ۱۸۰ درجه باشند. در یک چندضلعی محدب، تمام زاویهها از نوع حاده، قائمه و یا منفرجه هستند.
مثال ۱: تشخیص چندضلعی محدب با زاویههای معلوم
در تصویر زیر، کدام شکل چندضلعی محدب است؟
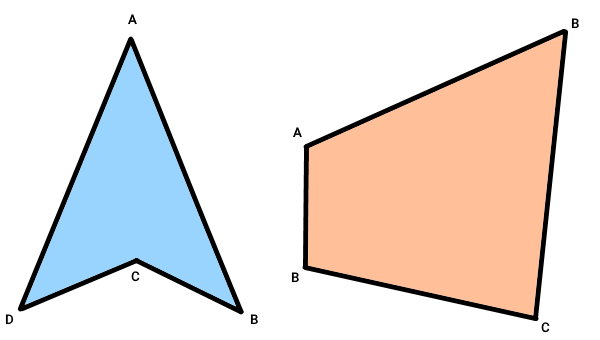
برای شکل سمت راست داریم:
۱۸۰° > A
۱۸۰° > B
۱۸۰° > C
۱۸۰° > D
بنابراین، چندضلعی سمت راست، محدب است. برای شکل سمت چپ داریم:
۱۸۰° > A
۱۸۰° > B
۱۸۰° < C
۱۸۰° > D
به دلیل اینکه زاویه C بزرگتر از ۱۸۰ درجه است، چندضلعی سمت چپ، غیر محدب (مقعر) محسوب میشود.
تشخیص چندضلعی محدب با استفاده از امتداد ضلعها
حاده، قائمه یا منفرجه بودن زاویههای یک چندضلعی، معمولا با چشم قابل تشخیص است. با این وجود، در صورت عدم اطمینان از نوع زاویه، میتوان از یک روش ساده استفاده کرد. زاویه یک خط راست، دقیقا برابر با ۱۸۰ درجه است. روش دوم تشخیص چندضلعی، با در نظر داشتن این نکته اجرا میشود. به منظور اجرای این روش، ابتدا باید تمام ضلعهای چندضلعی را امتداد دهیم.
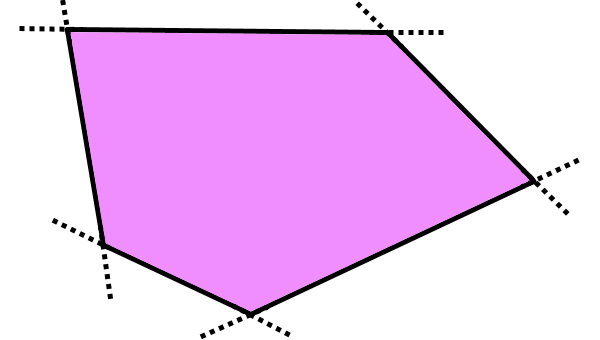
اگر تمام امتدادها بیرون از شکل قرار داشته باشند، زاویه تمام راسها کوچکتر از ۱۸۰ درجه خواهد بود (تصویر بالا). قرارگیری حداقل دو امتداد درون شکل، به معنای این است که حداقل یکی از راسهای چندضلعی، زاویهای بزرگتر از ۱۸۰ درجه دارد. در نتیجه، آن شکل نمیتواند محدب باشد.
مثال ۲: تشخیص چندضلعی محدب با زاویههای مجهول
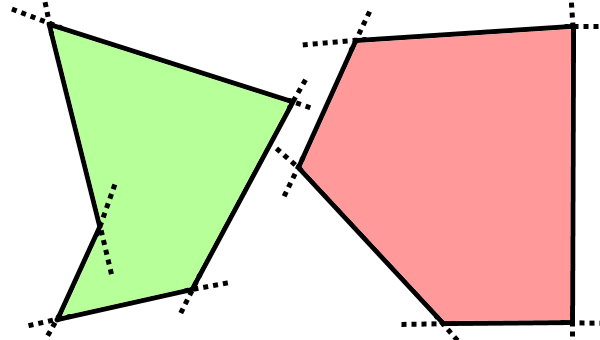
چندضلعی محدب را از بین دو شکل زیر پیدا کنید.
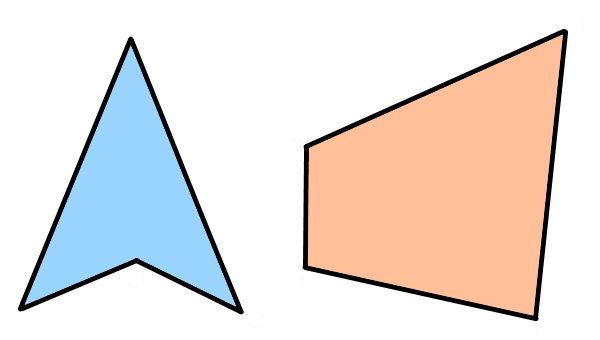
محدب یا غیر محدب بودن شکلهای بالا را در مثال ۱ مورد بررسی قرار دادیم. در اینجا، قصد داریم نوع چندضلعیها را به کمک امتداد ضلعها تعیین کنیم. به این منظور، تمام ضلعهای هر دو شکل را امتداد میدهیم.
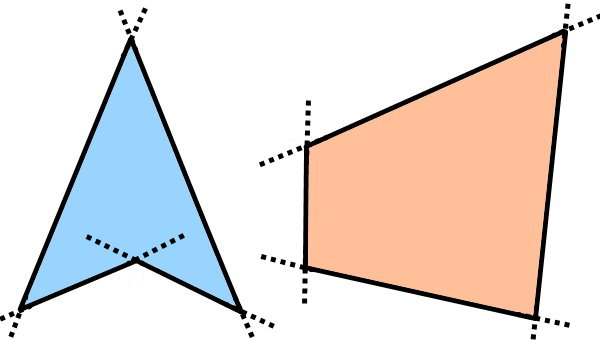
بر اساس تصویر بالا، امتداد دو ضلع چندضلعی سمت چپ از درون شکل عبور میکند. بنابراین، این چندضلعی، محدب نیست. در طرف مقابل، امتداد تمام ضلعهای چندضلعی سمت راست، در بیرون از شکل قرار دارد. از اینرو، این چندضلعی، محدب در نظر گرفته میشود.
تشخیص چندضلعی محدب با اتصال دو نقطه درون یا روی محیط
از اتصال دو نقطه به یکدیگر، یک خط راست تشکیل میشود. اگر دو نقطه بر روی محیط یا دو نقطه درون محیط یک چندضلعی را به هم وصل کنیم، یکی از سه حالت زیر به وجود میآید:
- خط اتصال دو نقطه، درون چندضلعی قرار میگیرد.
- خط اتصال دو نقطه، بر روی یکی از ضلعها منطبق میشود.
- بخشی از خط اتصال دو نقطه، ضلعهای چندضلعی را قطع میکند.
یک چندضلعی، محدب است؛ اگر هیچ دو نقطهای درون آن را نتوان پیدا کرد که خط اتصالشان، ضلعهای چندضلعی را قطع کند. نحوه استفاده از این روش را با یک مثال توضیح میدهیم.
مثال ۳: تعیین چندضلعیهای محدب
محدب یا غیر محدب بودن شکلهای مثال ۱ را توسط روش سوم تعیین کنید.
پس از بررسی شکلهای مثال ۱، به این نتیجه میرسیم که شکل راست، محدب هستند. هیچ دو نقطهای درون این چندضلعی وجود ندارد که خط اتصال آنها، ضلعهای چندضلعی را قطع کند. بر همین اساس، شکل چپ، غیر محدب است.
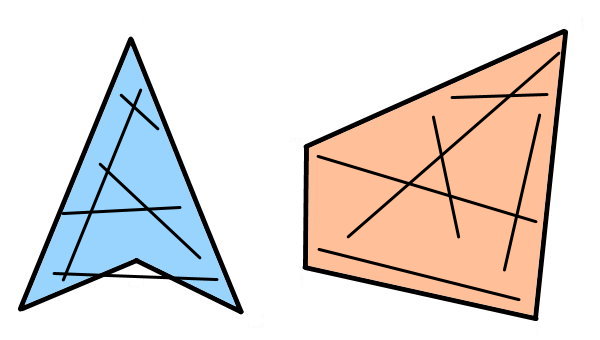
یکی دیگر از سادهترین روشهای تشخیص محدب بودن چندضلعیها، رسم قطرهای چندضلعی است. در بخشهای بعدی، به توضیح این روش خواهیم پرداخت.
زاویه داخلی چند ضلعی محدب چیست؟
به زاویههایی که در هر راس یک چند ضلعی محدب، بین دو ضلع تشکیل می شود، زاویه داخلی آن راس میگویند. مطابق با تعریف، تمام زاویههای داخلی چندضلعی محدب، کوچکتر از ۱۸۰ درجه هستند.
تصویر زیر، زوایای داخلی یک متوازیالاضلاع را نمایش میدهد.
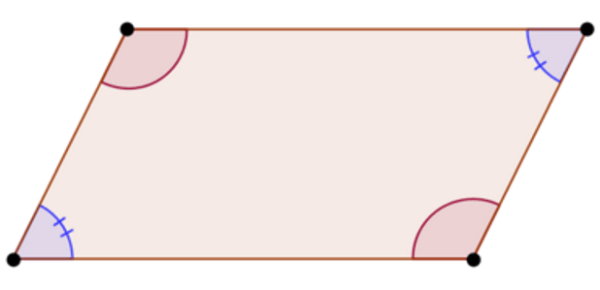
مجموع زوایای داخلی چند ضلعی های محدب چقدر است؟
مجموع زوایای داخلی چندضلعیها، به تعداد ضلعهای آنها بستگی دارد. فرمول مجموع زوایای داخلی چندضلعی محدب به صورت زیر نوشته میشود:
- S: مجموع زوایای داخلی چندضلعی محدب
- n: تعداد ضلعهای چندضلعی محدب
مثال ۴: محاسبه مجموع زوایای داخلی چندضلعی محدب
از میان دو شکل زیر، مجموع زوایای داخلی چند ضلعی محدب را بدست بیاورید.
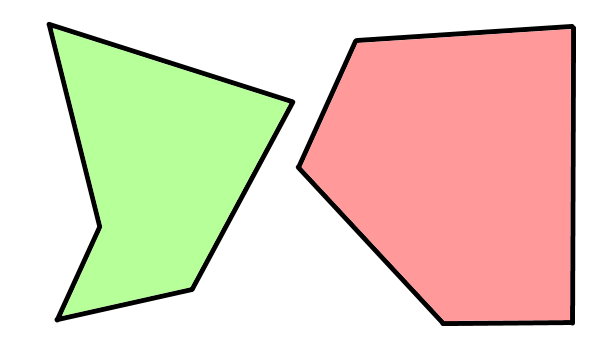
در تصویر بالا، دو شکل نمایش داده شده است. در ابتدا، چندضلعی محدب را مشخص میکنیم. به این منظور، ضلعهای دو شکل را امتداد میدهیم.
بر اساس امتداد ضلعها میتوانیم نتیجه بگیریم که شکل سمت راست، یک چندضلعی محدب است. این شکل، ۵ ضلع دارد. بنابراین، مجموع زوایای داخلی آن با استفاده از فرمول زیر محاسبه میشود:
- S: مجموع زوایای داخلی
- n: تعداد ضلعها برابر ۵
در نتیجه، مجموع زاویههای داخلی پنجضلعی محدب برابر ۵۴۰ درجه است.
مثال ۵: محاسبه یکی از زوایای داخلی چندضلعی محدب
مجموع شش زاویه داخلی یک هفتضلعی محدب برابر ۸۵۰ درجه است. اندازه زاویه هفتم این چندضلعی محدب را حساب کنید.
مجموع زوایای داخلی یک هفتضلعی محدب از رابطه زیر به دست میآید:
- S: مجموع زوایای داخلی
- n: تعداد ضلعها برابر ۷
مجموع هفت زاویه چندضلعی برابر ۹۰۰ درجه و مجموع شش زاویه آن برابر ۸۵۰ درجه است. بنابراین، زاویه هفتم این چندضلعی، از اختلاف این دو عدد محاسبه میشود:
مجموع شش زاویه - °۹۰۰ = زاویه هفتم
۸۵۰° - ۹۰۰° = زاویه هفتم
۵۰° = زاویه هفتم
زاویه خارجی چند ضلعی محدب چیست؟
به زاویههایی که در هر راس یک چند ضلعی محدب، بین یک ضلع و امتداد ضلع دیگر تشکیل میشود، زاویه خارجی آن راس میگویند. زاویه خارجی و داخلی چندضلعیهای محدب، مکمل یکدیگر هستند.
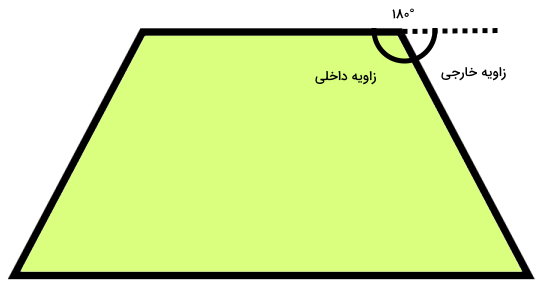
به عبارت دیگر، جمع هر زاویه داخلی با زاویه خارجی مجاور آن برابر با ۱۸۰ درجه میشود. تصویر زیر، یکی زوایای داخلی و زاویه خارجی مجاور آن در یک ذوزنقه را نمایش میدهد.
مجموع زوایای خارجی چند ضلعی های محدب چقدر است؟
مجموع زاویه های خارجی چندضلعی محدب، همواره برابر با ۳۶۰ درجه است. این عدد، ارتباطی به تعداد ضلعهای چندضلعی ندارد. به منظور اثبات مجموع زوایای خارجی چندضلعی محدب، تصویر زیر را در نظر بگیرید.
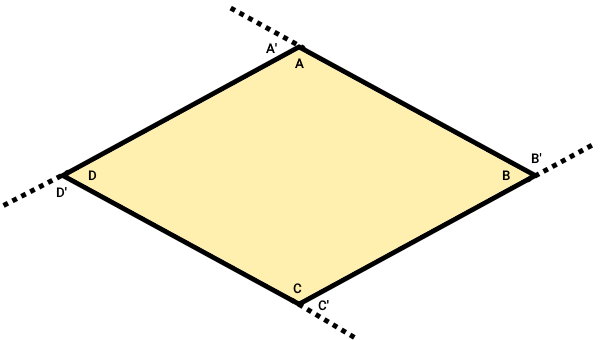
در تصویر بالا، زوایای داخلی و خارجی یک چهارضلعی محدب نمایش داده شدهاند. مجموع تمام زوایای داخلی و خارجی به صورت زیر نوشته میشود:
جمع هر زاویه داخلی با زاویه خارجی مجاورش برابر با ۱۸۰ درجه است. بنابراین داریم:
به عبارت دیگر، مجموع زوایای داخلی و خارجی چهارضلعی محدب برابر با ۷۲۰ درجه است:
اگر زوایای خارجی و داخلی را در کنار یکدیگر بنویسیم، رابطه بالا به شکل زیر درمیآید:
اولین پرانتز، مجموع زوایای داخلی و دومین پرانتز، مجموع زوایای خارجی را نمایش میدهد. مجموع زوایای داخلی یک چهار ضلعی محدب برابر است با:
- S: مجموع زوایای داخلی
- n: تعداد ضلعها برابر ۴
به این ترتیب داریم:
در نتیجه، مجموع زوایای خارجی چهارضلعی محدب برابر با ۳۶۰ درجه است. با تکرار این محاسبات برای هر چند ضلعی محدب، به جواب ۳۶۰ درجه خواهیم رسید. در صورت تمایل به یادگیری نحوه انجام این محاسبات برای چندضلعیهای مقعر، مطالعه مطلب «مجموع زوایای چندضلعی مقعر — به زبان ساده + حل تمرین و اثبات فرمول» را به شما پیشنهاد میکنیم.
چند ضلعی محدب منتظم چیست؟
به چندضلعیهایی که همه ضلعها و زوایههای آنها با یکدیگر هماندازه باشند، چندضلعی منتظم میگویند.
تمام چندضلعیهای منتظم، محدب هستند. مربع، شناخته شدهترین چندضلعی منتظم محدب است. این شکل هندسی، چهار ضلع برابر و چهار زاویه قائمه دارد.
اندازه زاویه داخلی چند ضلعی محدب منتظم چگونه بدست می آید؟
مجموع زوایای داخلی چندضلعی محدب منتظم، با استفاده از فرمول زیر محاسبه میشود:
- S: مجموع زوایای داخلی
- n: تعداد ضلعها
تمام زاویههای چندضلعی منتظم با یکدیگر برابر هستند. بنابراین، اندازه هر زاویه یک n ضلعی محدب منتظم، از تقسیم مجموع زوایای داخلی آن بر تعداد ضلعها (n) به دست میآید:
مثال ۶: محاسبه زاویه داخلی چندضلعی محدب منتظم
اندازه هر یک از زاویههای داخلی یک هشت ضلعی منتظم، چقدر است؟
تمام چندضلعیهای منتظم، محدب هستند. بنابراین، به منظور محاسبه هر یک از زاویههای یک هشت ضلعی منتظم میتوانیم از فرمول زیر استفاده کنیم:
- θ: زاویه داخلی چندضلعی منتظم
- n: تعداد ضلعهای چندضلعی منتظم برابر با ۸
در نتیجه، اندازه هر یک از زاویههای داخلی یک هشتضلعی منتظم برابر با ۱۳۵ درجه است.

اندازه زاویه خارجی چند ضلعی محدب منتظم چگونه بدست می آید؟
مجموع اندازه زاویههای خارجی تمام چندضلعیهای محدب (منتظم و غیر منتظم) برابر با ۳۶۰ درجه است. در چندضلعیهای منتظم، به دلیل برابر بودن تمام زاویههای داخلی، تمام زاویههای خارجی نیز با هم برابر خواهند بود. بنابراین، اندازه هر یک از زاویههای خارجی از تقسیم عدد ۳۶۰ بر تعداد ضلعها محاسبه میشود:
- β: زاویه خارجی چندضلعی منتظم
- n: تعداد ضلعهای چندضلعی منتظم
مثال ۷: محاسبه زاویه خارجی چندضلعی محدب
تمام ضلعهای یک ششضلعی محدب، هماندازه هستند. اندازه هر زاویه خارجی این ششضلعی را به دست بیاورید.
اگر اندازه ضلعهای یک چندضلعی محدب یکسان باشد، آن چندضلعی، منتظم است و تمام زاویههای خارجی آن با هم برابر هستند. با توجه به این نکته، اندازه هر زاویه خارجی ششضلعی از رابطه زیر تعیین میشود:
- β: زاویه خارجی
- n: تعداد ضلعها برابر ۶
در نتیجه، هر یک از زاویههای خارجی یک ششضلعی محدب منتظم برابر با ۷۲ درجه است.
قطر چند ضلعی محدب چیست؟
قطر چندضلعی محدب، پارهخطی است که دو راس غیر مجاور را به یکدیگر وصل میکند. تمام قطرهای چندضلعیهای محدب، درون محیط آنها قرار میگیرند. از اینرو، با رسم قطرهای یک چندضلعی و بررسی قرارگیری آنها درون محیط، میتوان محدب یا غیر محدب بودن چندضلعی را تشخیص داد.
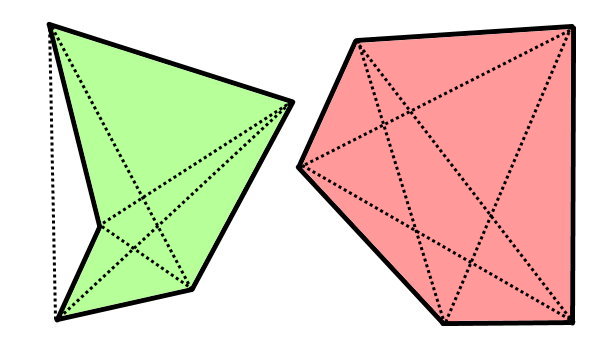
فرمول تعداد قطرهای چند ضلعی محدب چیست؟
تعداد قطرهای چندضلعی محدب، به تعداد راسهای آن بستگی دارد. بر این اساس، فرمول تعداد قطرهای چندضلعی محدب برابر است با:
- d: تعداد قطرها
- n: تعداد راسها
مثال ۸: محاسبه تعداد قطرهای چندضلعی محدب
سهضلعی محدب چند قطر دارد؟
تعداد قطرهای یک سهضلعی محدب (مثلث)، از رابطه زیر به دست میآید:
- d: تعداد قطرها
- n: تعداد راسها برابر با ۳
در نتیجه، سهضلعی محدب یا همان مثلث، هیچ قطری ندارد. مثلث، تنها شکل چندضلعی محدب با تعداد قطرهای صفر است.
مثال ۹: محاسبه تعداد قطرهای هشتضلعی محدب
تعداد قطرهای هشتضلعی محدب را حساب کنید.
تعداد قطرهای هشتضلعی محدب به صورت زیر محاسبه میشود:
- d: تعداد قطرها
- n: تعداد راسها برابر ۸
در نتیجه، هشتضلعی محدب، ۲۰ قطر دارد.
محور تقارن چند ضلعی محدب چیست؟
محور تقارن چندضلعی محدب، پارهخطی است که آن را به دو قسمت مساوی تقسیم میکند. بسیاری از چندضلعیهای محدب نظیر مربع، لوزی، مستطیل و غیره، حداقل یک محور تقارن دارند.
محورهای تقارن، از مرکز شکل عبور میکنند. تصویر زیر، محورهای تقارن سه سهضلعی محدب (مثلث متساوی الاضلاع، مثلث متساوی الساقین و مثلث مختلف الاضلاع) را نمایش میدهد.
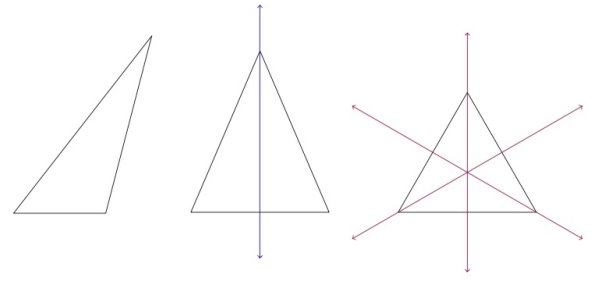
مثلث متساوی الاضلاع، یک سهضلعی محدب منتظم است. این شکل، سه محور تقارن دارد. تعداد محورهای تقارن مثلث متساوی الساقین برابر با یک است. مثلث مختلفالاضلاع نیز هیچ محور تقارنی ندارد.
چندضلعی محدب منتظم چند محور تقارن دارد؟
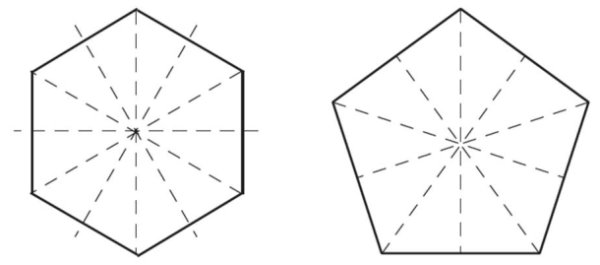
تمام چندضلعیهای محدب منتظم، دارای محور تقارن هستند. تعداد محورهای تقارن این شکلها، برابر با تعداد ضلعها است. به عنوان مثال، هر مربع، چهار محور تقارن و هر پنجضلعی منتظم، پنج محور تقارن دارد. در زوج ضلعی منتظم، نیمی از محورهای تقارن، از اتصال راسهای روبهرویی به وجود میآیند. نیمِ دیگر محورهای تقارن، خطهای عبوری از مرکز ضلعهای روبهرویی هستند. در فردضلعی منتظم، با رسم پارهخطی بین هر راس تا مرکز ضلع مقابل آن راس، یکی از محورهای تقارن ایجاد میشود.
مثال ۱۰: تعیین محورهای تقارن چندضلعی محدب
محورهای تقارن هشتضلعی منتظم زیر را رسم و تعداد آنها را حساب کنید.
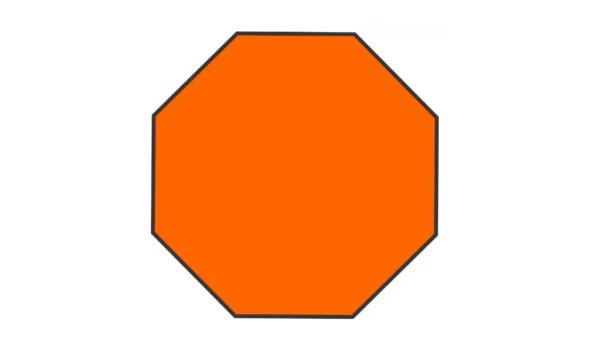
شکل بالا، یک زوج ضلعی محدب و منتظم است. برای رسم محورهای تقارن این شکل، راسهای روبهرویی را به هم وصل میکنیم. پارهخطهای رسم شده، نیمی از محورهای تقارن شکل هستند.

بهمنظور رسم محورهای تقارن بعدی، مرکز هر ضلع را به مرکز ضلع متصل میکنیم. اکنون، تمام محورهای تقارن ششضلعی منتظم را داریم.
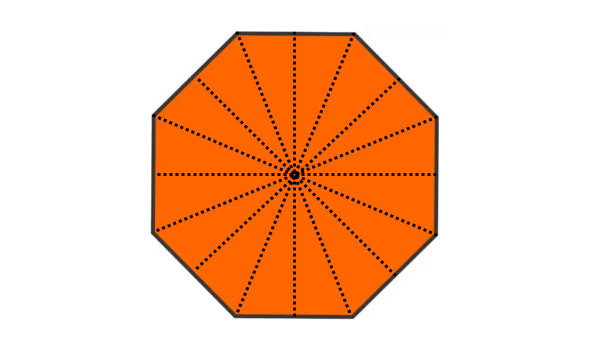
تعداد محورهای تقارن ششضلعی منتظم برابر با شش است.
محیط و مساحت چند ضلعی محدب چگونه بدست می آید؟
محیط، معیاری برای تعیین اندازه دور یک شکل هندسی است. محیط چندضلعی محدب، از جمع طول هر یک از ضلعهای آن با یکدیگر به دست میآید. به عنوان مثال، محیط سهضلعی محدب برابر است با:
ضلع سوم + ضلع دوم + ضلع اول = محیط سهضلعی محدب
البته، نحوه محاسبه محیط در انواع مختلف شکلهای محدب، با یکدیگر تفاوت دارد. به عنوان مثال، محیط چندضلعی محدب منتظم، با ضرب اندازه یک ضلع در تعداد ضلعها تعیین میشود. بر اساس این رابطه، محیط یک چهارضلعی محدب منتظم برابر است با:
اندازه ضلع × ۴ = محیط چهارضلعی منتظم
مساحت، اندازه سطح درون یک شکل هندسی بسته را نمایش میدهد. مساحت هر چندضلعی محدب، فرمول مخصوص به خود را دارد. برای آشنایی با نحوه محاسبه محیط و مساحت چندضلعیهای محدب، مطالعه مطلب «فرمول های محیط و مساحت اشکال هندسی (+ فیلم و PDF رایگان)» را به شما پیشنهاد میکنیم.
جمعبندی ویژگی های چند ضلعی محدب
در این مقاله، چندضلعیهای محدب و مباحث مرتبط با آنها را مورد بررسی قرار دادیم. در انتها، به منظور مرور سریع مطالب ارائه شده، برخی از مهمترین خواص چند ضلعی محدب را معرفی میکنیم:
- تمام زاویههای داخلی چندضلعی محدب، کوچکتر از ۱۸۰ درجه هستند.
- اگر حداقل یکی از زاویههای داخلی چندضلعی، بزرگتر از ۱۸۰ درجه باشد، به آن چندضلعی، غیر محدب یا مقعر (کاو) میگویند.
- مجموع زوایای داخلی تمام چندضلعیهای محدب از رابطه S=(n-۲)×۱۸۰° به دست میآید.
- قطرهای چندضلعیهای محدب، به طور کامل درون محیط این شکلها قرار میگیرند.
- هر چندضلعی محدب را میتوان به صورت مجموعهای از مثلثها نمایش داد.
- مساحت چندضلعیهای محدب، برابر با مجموع مساحت مثلثهای تشکیلدهنده آن است.
سوالات متداول در رابطه با چند ضلعی های محدب
در این بخش، به برخی از سوالات پرتکرار در رابطه با چندضلعیهای محدب و ویژگیهای آنها به طور خلاصه پاسخ میدهیم.
تعریف چند ضلعی محدب چیست؟
به چندضلعیهایی با زوایای کوچکتر ۱۸۰ درجه، چندضلعی محدب گفته میشود.
نام دیگر چند ضلعی محدب چیست ؟
نام دیگر چندضلعی محدب، چندضلعی کوژ است.
انواع چند ضلعی های محدب چه هستند؟
چندضلعیهای محدب به دو نوع منتظم (ضلعهای برابر) و غیر منتظم (حداقل دو ضلع نابرابر) تقسیم میشوند.
کوچکترین چند ضلعی محدب چیست ؟
کوچکترین چندضلعی محدب از نظر تعداد ضلعها، مثلث نام دارد.
آیا همه چند ضلعی های منتظم محدب هستند؟
بله. چندضلعیهای منتظم نمیتوانند مقعر باشند؛ چراکه در چندضلعیهای مقعر، تمام زاویهها هماندازه نیستند.
آیا مستطیل یک چند ضلعی محدب است؟
بله. مستطیل، شکلی با چهار زاویه ۹۰ درجه است.
آیا لوزی یک چند ضلعی محدب است؟
بله. لوزی، شکلی با چهار ضلع برابر است که دو زاویه حاده برابر و دو زاویه منفرجه برابر دارد. با این وجود، هیچیک از زاویههای این شکل، بزرگتر از ۱۸۰ درجه نیست.
آیا ذوزنقه یک چند ضلعی محدب است؟
بله.
چند ضلعی محدب حداکثر چند زاویه تند دارد ؟
هر چندضلعی محدب، میتواند حداکثر سه زاویه کمتر از ۹۰ درجه (تند یا حاده) داشته باشد.
آیا شکل ستاره محدب است؟
خیر. چندضلعیهای ستارهای شکل، مقعر هستند.
چند ضلعی که محدب نباشد چیست؟
چند ضلعی که محدب نباشد، مقعر است.
تفاوت چند ضلعی محدب و مقعر چیست؟
چندضلعی مقعر، حداقل یک زاویه بزرگتر از ۱۸۰ درجه دارد؛ در صورتی که هیچ از زاویههای چندضلعی محدب، بزرگتر از ۱۸۰ درجه نیستند.
آیا یک چندضلعی می تواند هم محدب و هم مقعر باشد؟
خیر. یک چندضلعی میتواند یا محدب یا مقعر باشد و حالت دیگری وجود ندارد.
ترکیب چندضلعی مقعر و محدب چه میشود؟
ترکیب شکلهای مکمل مقعر و محدب، یک چندضلعی محدب است.<۱۸۰°
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش انواع چند ضلعی ها — تعاریف و تمامی فرمول های محیط و مساحت» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- چند ضلعی چیست ؟ — به زبان ساده
- چند ضلعی محدب چیست ؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده(همین مطلب)
- چند ضلعی مقعر چیست ؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده
- چند ضلعی منتظم چیست ؟ — به زبان ساده + فیلم آموزش رایگان و حل تمرین
- مجموع زوایای داخلی چند ضلعی محدب چیست ؟ — به زبان ساده + حل مثال
- مجموع زوایای خارجی چند ضلعی محدب چیست ؟ — به زبان ساده + حل مثال
- فرمول بدست آوردن مجموع زوایای داخلی چند ضلعی + حل تمرین
- مجموع زوایای چند ضلعی مقعر — به زبان ساده + حل تمرین و اثبات فرمول
- مجموع زوایای خارجی چند ضلعی منتظم — به زبان ساده + اثبات
- مساحت چند ضلعی منتظم چگونه بدست می آید ؟ — به زبان ساده + حل مثال
- محور تقارن چند ضلعی منتظم چیست ؟ — به زبان ساده












