محیط متوازی الاضلاع چیست؟ — به زبان ساده + حل تمرین و مثال

محیط متوازی الاضلاع برابر جمع تمام ضلع‌های آن است. این اندازه از رابطه «مجموع دو ضلع مجاور ضربدر دو» نیز به دست می‌آید. در این آموزش، به معرفی نحوه محاسبه محیط متوازی الاضلاع به همراه حل چند مثال متنوع می‌پردازیم. علاوه بر این، فرمول‌های محیط متوازی الاضلاع با قطر و ارتفاع و سایت‌های محاسبه آنلاین محیط را نیز ارائه می‌کنیم.

متوازی الاضلاع چیست؟

متوازی الاضلاع، یک شکل چهار ضلعی است که دو ضلع روبه‌رویی آن با مساوی و موازی هستند. مربع، مستطیل و لوزی، از انواع خاص متوازی الاضلاع محسوب می‌شوند.

محیط متوازی الاضلاع چیست؟

محیط متوازی الاضلاع، اندازه دور این شکل هندسی است. تصویر زیر، یک متوازی الاضلاع را نمایش می‌دهد. مداد خود را بر روی یکی از گوشه‌های متوازی الاضلاع قرار داده و آن را بر روی تمام ضلع‌ها حرکت می‌دهیم. با برگشتن به نقطه شروع، مداد، به اندازه محیط متوازی الاضلاع حرکت می‌کند.

محیط متوازی الاضلاع چگونه بدست می آید ؟

محیط متوازی الاضلاع، از جمع اندازه تمام ضلع‌های آن به دست می‌آید. متوازی الاضلاع زیر را در نظر بگیرید.

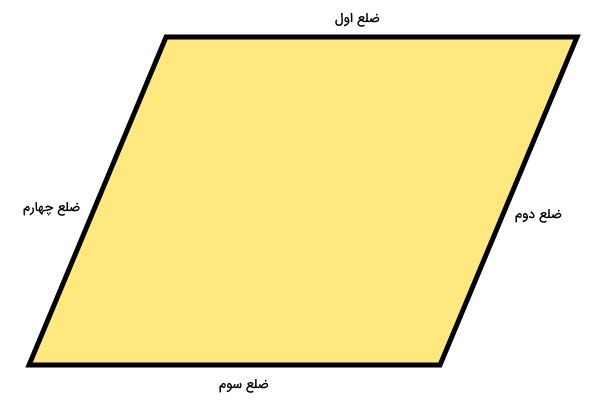
بر اساس تعریف، محیط متوازی الاضلاع بالا به صورت زیر محاسبه می‌شود:

ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط متوازی الاضلاع

در متوازی الاضلاع، اندازه ضلع‌های روبه‌رویی با هم برابر است. به همین دلیل می‌توانیم رابطه بالا را به صورت زیر بازنویسی کنیم:

ضلع دوم + ضلع اول + ضلع دوم + ضلع اول = محیط متوازی الاضلاع

(ضلع دوم × 2) + (ضلع اول × 2) =

(ضلع دوم + ضلع اول) × 2 =

ضلع اول و دوم در متوازی الاضلاع بالا، در کنار یکدیگر یا اصطلاحا مجاور هستند. از این‌رو، بهتر است فرمول محیط متوازی‌الاضلاع را به صورت زیر بنویسیم:

(جمع دو ضلع مجاور) × 2 = محیط متوازی الاضلاع

مثال 1: محاسبه محیط متوازی الاضلاع به دو روش

محیط متوازی الاضلاع زیر را به دو روش حساب کنید.

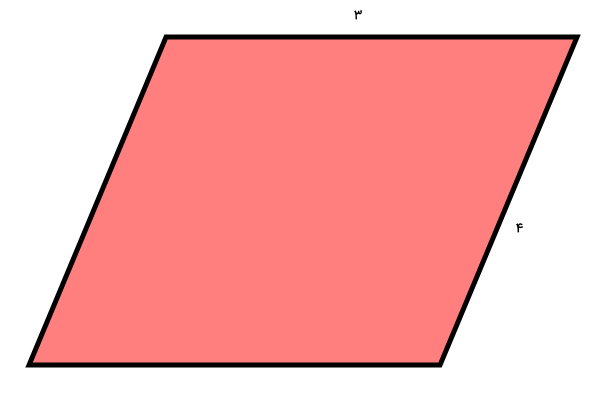
در متوازی الاضلاع بالا، فقط اندازه دو ضلع مجاور داده شده است. ضلع‌های روبه‌رویی در متوازی الاضلاع، هم‌اندازه‌اند. بنابراین، اندازه تمام ضلع‌ها را می‌دانیم.

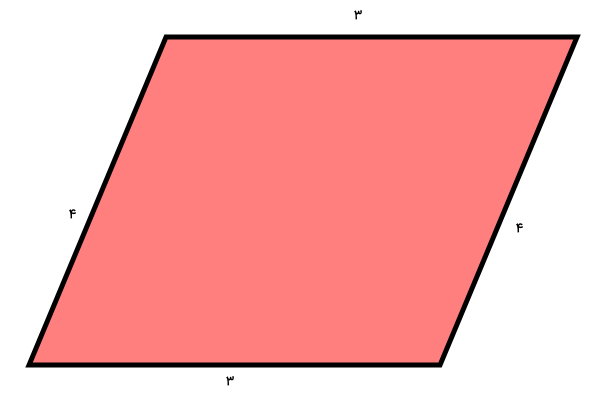
برای محاسبه محیط متوازی الاضلاع، دو روش وجود دارد. روش اول، با جمع تمام اندازه‌ها انجام می‌شود:

ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط متوازی الاضلاع

4 + 3 + 4 + 3 =

14 =

روش دوم محاسبه محیط، استفاده از رابطه مخصوص به آن است:

(جمع دو ضلع مجاور) × 2 = محیط متوازی الاضلاع

(4 + 3) × 2 =

(7) × 2 =

14 =

همان‌طور که مشاهده می‌کنید، نتیجه هر دو روش برابر است.

مثال ۲: محاسبه ضلع متوازی الاضلاع از روی محیط و ضلع دیگر

مجموع اندازه ضلع‌های یک متوازی الاضلاع برابر 76 سانتی‌متر و اندازه یکی از ضلع‌های آن برابر 21 سانتی‌متر است. اندازه تمام ضلع‌های این متوازی الاضلاع را تعیین کنید.

در صورت مسئله اندازه دور (محیط) متوازی الاضلاع و یکی از ضلع‌های آن داده شده است. با استفاده از این اطلاعات می‌توانیم اندازه ضلع مجاور ضلع معلوم را به دست بیاوریم:

(ضلع مجاور + ضلع) × 2 = محیط

آموزش ریاضی پایه هفتم

شروع یادگیری

آموزش ریاضی – پایه نهم

شروع یادگیری

آموزش نگارش – پایه هفتم

شروع یادگیری

آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی

شروع یادگیری

آموزش ریاضیات گسسته – پایه دوازدهم

شروع یادگیری

آموزش عربی – پایه نهم

شروع یادگیری

آموزش محاسبات سریع ریاضی

شروع یادگیری

آموزش ریاضی و آمار ۱ – پایه دهم علوم انسانی

شروع یادگیری

آموزش ریاضی – پایه هشتم

شروع یادگیری

آموزش هندسه پایه دهم – هندسه ۱

شروع یادگیری

(ضلع مجاور + 21) × 2 = 76

2 ÷ 76 = ضلع مجاور + 21

38 = ضلع مجاور + 21

21 – 38 = ضلع مجاور

17 = ضلع مجاور

اندازه دو ضلع متوازی اضلاع برابر 21 و 17 سانتی‌متر است. ضلع‌های روبه‌رویی متوازی اضلاع، دارای اندازه برابر هستند. در نتیجه، دو ضلع دیگر نیز 21 و 17 سانتی‌متر خواهند بود.

مثال 3: محاسبه محیط متوازی الاضلاع از روی مساحت

مساحت یک متوازی الاضلاع برابر 40 میلی‌‌متر مربع، ارتفاع آن برابر 10 میلی‌متر و اندازه یکی از ضلع‌های آن برابر 12 میلی‌متر است. محیط متوازی الاضلاع را حساب کنید.

مساحت متوازی الاضلاع، از ضرب ارتفاع در قاعده آن به دست می‌آید:

قاعده × ارتفاع = مساحت متوازی الاضلاع

قاعده × 10 = 40

10 ÷ 40 = قاعده

4 = قاعده

قاعده متوازی الاضلاع برابر 4 میلی‌متر است. قاعده، یکی از ضلع‌های متوازی الاضلاع محسوب می‌شود. ضلع دیگر نیز در صورت مسئله داده شده است (12 میلی‌متر). به این ترتیب می‌توانیم محیط را از فرمول زیر حساب کنیم:

(قاعده + ضلع) × 2 = محیط متوازی الاضلاع

(4 + 12) × 2 =

(16) × 2 =

32 =

در نتیجه، محیط متوازی الاضلاع برابر 32 میلی‌متر است.

مثال 4: محاسبه محیط متوازی الاضلاع کسری

محیط متوازی الاضلاع زیر را به صورت کسری به دست بیاورید.

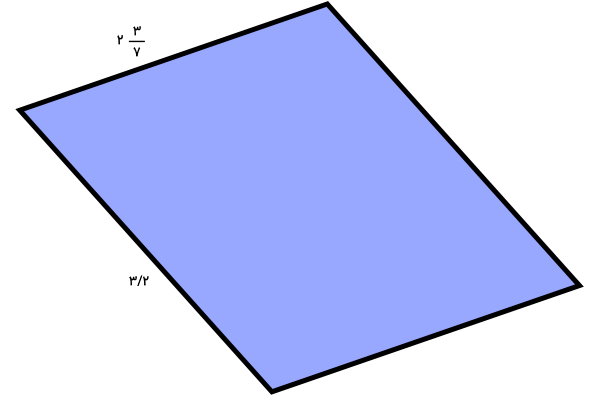
اندازه یک ضلع و ضلع مجاور آن در تصویر بالا به صورت کسر نوشته شده‌اند. یکی از این اندازه‌ها، عدد مخلوط و دیگری، عدد اعشاری است. این اعداد را درون فرمول قرار می‌دهیم:

(مجموع ضلع‌های مجاور) × 2 = محیط متوازی الاضلاع

$$
= ۲ \times (۲ \frac {۳}{۷} + ۳/۲)
$$

به منظور تعیین محیط، باید دو کسر بالا را با یکدیگر جمع کنیم. ساده‌ترین روش برای انجام این کار، تبدیل هر عدد به یک کسر ساده و جمع آن‌ها است. در ادامه، شکل ساده شده اندازه ضلع‌ها را مشاهده می‌کنید:

$$
۲ \frac {۳}{۷} = \frac {(۲ \times ۷) +۳}{۷} = \frac {(۱۴)+۳}{۷} = \frac {۱۷}{۷}
$$

$$
۳/۲ = \frac {۳۲}{۱۰}
$$

اکنون، شکل ساده کسرها را درون فرمول محیط می‌گذاریم:

$$
= ۲ \times (\frac {۱۷}{۷} + \frac {۳۲}{۱۰})
$$

برای جمع کسرهای ساده، مخرج آن‌ها باید مشترک باشد. در غیر این‌صورت (مانند حالت بالا)، باید از آن‌ها مخرج مشترک بگیریم. به این ترتیب داریم:

$$
= ۲ \times (\frac {۱۷ \times ۱۰}{۷\times ۱۰} + \frac {۳۲ \times ۷}{۱۰\times ۷})
$$

$$
= ۲ \times (\frac {۱۷۰}{۷۰} + \frac {۲۲۴}{۷۰})
$$

$$
= ۲ \times (\frac {۱۷۰ + ۲۲۴}{۷۰})
$$

$$
= ۲ \times (\frac {۳۹۴}{۷۰})
$$

$$
= \frac {۲ \times۳۹۴}{۷۰}
$$

$$
= \frac {۷۸۸}{۷۰}
$$

عدد بالا، محیط متوازی الاضلاع را به صورت کسری نمایش می‌دهد.

فرمول محیط متوازی الاضلاع به صورت جبری چیست؟

عبارت‌های جبری، ترکیبی از اعداد، متغیرها و عمل‌های ریاضی هستند که به منظور نمایش رابطه بین اندازه‌های مختلف مورد استفاده قرار می‌گیرند. به عنوان مثال، تصویر زیر، اندازه دو ضلع مجاور در یک متوازی الاضلاع را با متغیرهای a و b نمایش می‌دهد.

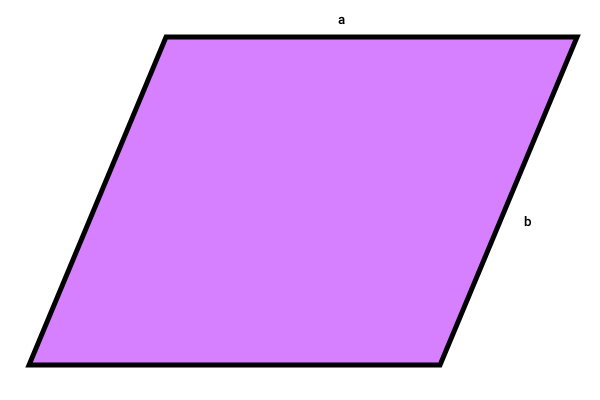
محیط شکل بالا برابر است با:

a + b + a + b = محیط

۲a + 2b = محیط

(a + b) × ۲ = محیط

در ریاضیات، محیط شکل‌های مختلف را با حرف P (ابتدای کلمه Perimeter) نمایش می‌دهند. بر این اساس، فرمول محیط متوازی الاضلاع با عبارت جبری به صورت زیر نوشته می‌شود:

$$
P = ۲ \times (a+b)
$$

مثال 5: محاسبه محیط متوازی الاضلاع به صورت جبری

اندازه یکی از ضلع‌های یک متوازی الاضلاع، برابر 7 متر و اندازه ضلع مجاور آن برابر 13 متر است. محیط این متوازی الاضلاع را به دست بیاورید.

به منظور شروع حل مسئله، فرمول محیط را می‌نویسیم و اندازه‌های معلوم را مشخص می‌کنیم:

$$
P = ۲ \times (a+b)
$$

• S: محیط
• a: اندازه یکی از ضلع‌ها برابر 7 متر
• b: اندازه ضلع مجاور a برابر 13 متر

اندازه‌های معلوم را درون فرمول قرار می‌دهیم:

$$
P = ۲ \times (۷+۱۳)
$$

آموزش مدیریت تمرکز و توجه و راه های افزایش آن

شروع یادگیری

آموزش ریاضی و آمار ۲ – پایه یازدهم علوم انسانی

شروع یادگیری

آموزش ریاضی و آمار ۲ – پایه یازدهم علوم انسانی

شروع یادگیری

آموزش علوم تجربی – پایه هشتم – بخش شیمی

شروع یادگیری

آموزش افزایش تمرکز و تقویت حافظه

شروع یادگیری

آموزش عربی، زبان قرآن ۳ – رشته ادبیات و علوم انسانی

شروع یادگیری

آموزش منطق – پایه دهم

شروع یادگیری

آموزش ریاضی ۲ – پایه یازدهم علوم تجربی

شروع یادگیری

آموزش اصول مطالعه درسی – روش PQ6R برای یادگیری بهتر

شروع یادگیری

آموزش عربی، زبان قرآن ۱ – پایه دهم

شروع یادگیری

آموزش زبان انگلیسی ۲ – پایه یازدهم

شروع یادگیری

$$
P = ۲ \times (۲۰)
$$

$$
P = ۴۰
$$

در نتیجه، محیط برابر ۴۰ متر است.

فرمول محیط متوازی الاضلاع با قطر

قطرهای متوازی الاضلاع، پاره‌خط‌هایی هستند که دو گوشه مقابل در این شکل هندسی را به یکدیگر وصل می‌کنند. متوازی الاضلاع، دو قطر دارد. قطرهای متوازی الاضلاع، همدیگر را نصف می‌کنند.

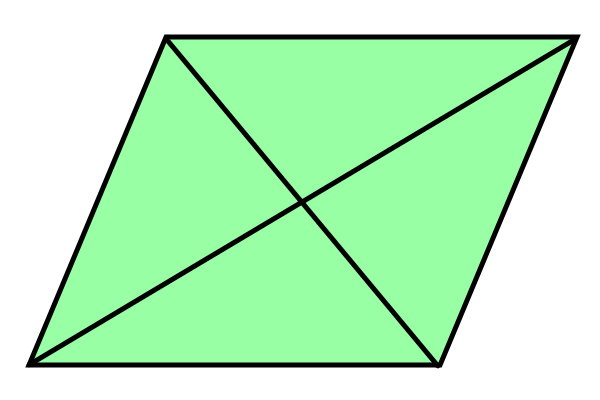
اگر اندازه هر دو قطر متوازی الاضلاع و اندازه یکی از ضلع‌های آن مشخص باشد، امکان محاسبه محیط فراهم می‌شود. فرمول محیط متوازی الاضلاع با قطر عبارت است از:

$$
P = ۲a +\sqrt{۲x^۲+۲y^۲-۴a^۲}
$$

• P: محیط
• a: یکی از ضلع‌ها
• x: قطر اول
• y: قطر دوم

فرمول محیط متوازی الاضلاع با قاعده و ارتفاع

قاعده متوازی الاضلاع، ضلعی است که در پایین این شکل هندسی قرار می‌گیرد. ارتفاع متوازی الاضلاع نیز، پاره‌خطی است که از راس مقابل قاعده بر آن عمود می‌شود. تصویر زیر، قاعده و ارتفاع یک متوازی الاضلاع را نمایش می‌دهد.

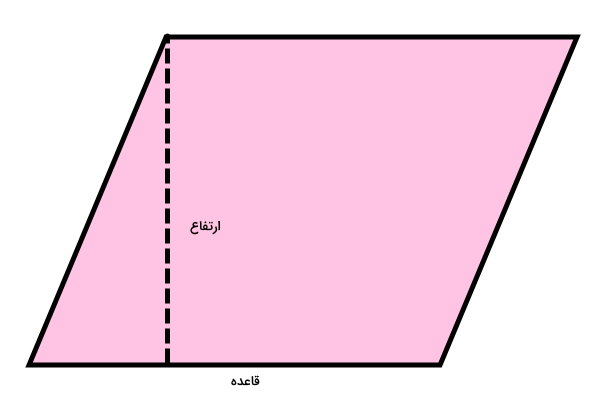
در اغلب موارد، قاعده و ارتفاع متوازی الاضلاع به منظور تعیین مساحت مورد استفاده قرار می‌گیرند. با این وجود، این دو اندازه به تنهایی برای محاسبه محیط قابل استفاده نیستند. فقط در صورتی که علاوه بر ارتفاع و قاعده، اندازه یکی از زاویه‌های داخلی را داشته باشیم، می‌توانیم محیط توسط فرمول زیر حساب کنیم:

$$
P =۲a + \frac {۲h} {\sin {\theta}}
$$

محاسبه آنلاین محیط متوازی الاضلاع

امروزه، ابزارهای اینترنتی زیادی در زمینه انجام محاسبات مربوط به شکل‌های هندسی مختلف از جمله متوازی الاضلاع وجود دارند. از بهترین محاسبه‌گرهای محیط متوازی الاضلاع به صورت آنلاین می‌توان به موتور جستجوی گوگل (+) و سایت تخصصی Omni Calculator (+) اشاره کرد. با جستجوی عبارتی نظیر «parallelogram perimeter» در سایت گوگل، کادر محاسبه محیط متوازی الاضلاع با دو ضلع ظاهر می‌شود.

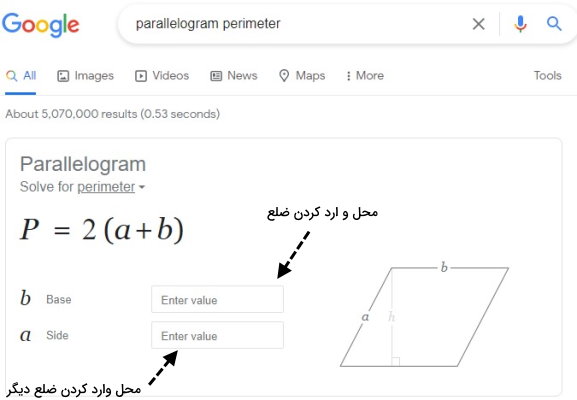
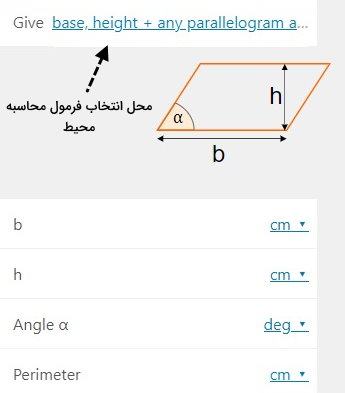
کار با ابزار محاسباتی گوگل ساده است اما امکان محاسبه محیط با قطر یا ارتفاع را فراهم نمی‌کند. به منظور محاسبه محیط توسط تمام فرمول‌های موجود، ابزار سایت Omni Calculator گزینه بهتری است.

سوالات متداول در رابطه با محیط متوازی الاضلاع

در این بخش، به برخی از سوالات پرتکرار در رابطه با محیط متوازی الاضلاع به طور خلاصه پاسخ می‌دهیم.

تعریف محیط متوازی الاضلاع چیست ؟

محیط متوازی الاضلاع، اندازه دور این شکل هندسی است.

محیط متوازی الاضلاع چند است ؟

محیط متوازی الاضلاع، برابر جمع اندازه چهار ضلع آن است.

رابطه محیط متوازی الاضلاع به زبان ساده چیست ؟

رابطه کلامی و ساده محیط متوازی الاضلاع، «مجموع اندازه دو ضلع مجاور ضربدر در 2» است.

محیط متوازی الاضلاع با عبارت جبری چیست؟

فرمول ریاضی یا عبارت جبری محیط متوازی الاضلاع‌، «P=2a+2b» است.