محیط متوازی الاضلاع به صورت جبری — فرمول های ریاضی + حل مثال

P=2a+2b، نمایش فرمول محیط متوازی الاضلاع به صورت جبری است. عبارت‌های جبری، یکی از ابزارهای پرکاربرد ریاضی برای نمایش فرمول‌ها و رابطه بین متغیرها هستند. در این آموزش، ضمن تعریف کلی عبارت‌های جبری، فرمول‌ها و روش‌های محاسبه محیط متوازی الاضلاع به صورت جبری را مرور می‌کنیم.

عبارت جبری چیست؟

«عبارت جبری» (Algebraic Expression)، ترکیبی از اعداد (ثابت‌ها)، حروف (متغیرها) و عملگرها (جمع، تفریق، ضرب و غیره) است.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

با کنار هم قرار دادن اجزای یک عبارت جبری، یک رابطه یا فرمول ریاضی به وجود می‌آید. به عنوان مثال، فرمول زیر، عبارت جبری محیط مربع را نمایش می‌دهد:

$$
P=۴a
$$

حرف P، متغیر معرف محیط و حرف a، متغیر معرف ضلع مربع است. عدد 4، ثابت این عبارت جبری محسوب می‌شود.

محیط متوازی الاضلاع چیست و چگونه بدست می‌آید؟

متوازی‌الاضلاع، یکی از انواع چهارضلعی‌ها است. با جمع اندازه هر چهار ضلع متوازی‌الاضلاع، محیط آن به دست می‌آید. به عبارت دیگر، محیط متوازی‌الاضلاع، اندازه دور آن یا اندازه تمام ضلع‌های آن است.

فرمول محیط متوازی الاضلاع به صورت زیر نوشته می‌شود:

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

ضلع دوم + ضلع اول + ضلع دوم + ضلع اول = محیط متوازی‌الاضلاع

به دلیل برابر بودن ضلع‌های روبه‌رویی در متوازی‌الاضلاع، می‌توانیم فرمول بالا را به فرم‌های زیر بنویسیم:

(ضلع دوم × 2) + (ضلع اول × 2) = محیط متوازی‌الاضلاع

(ضلع دوم + ضلع اول) × 2 = محیط متوازی‌الاضلاع

(جمع دو ضلع مجاور) × 2 = محیط متوازی الاضلاع

برای یادگیری نحوه نوشتن فرمول محیط متوازی الاضلاع به صورت جبری، روابط کلامی بالا را به خاطر داشته باشید.

فرمول محیط متوازی الاضلاع به صورت جبری چیست؟

فرمول محیط متوازی الاضلاع به صورت جبری، P=2a+2b است. همان‌طور که مشاهده می‌کنید، این فرمول، از ترکیب حروف، اعداد و عملگرهای ریاضی تشکیل می‌شود. برای درک بهتر عبارت جبری محیط متوازی‌الاضلاع، شکل زیر را در نظر بگیرید.

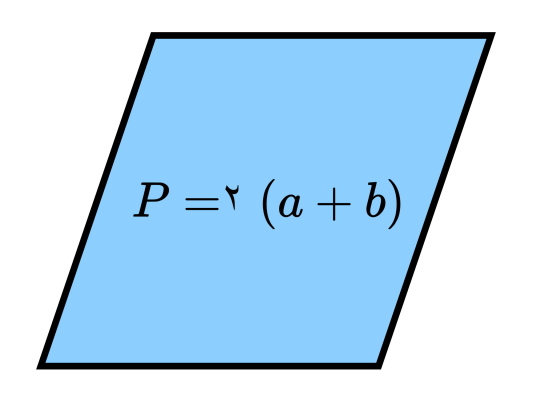
اندازه ضلع‌های متوازی‌الاضلاع بالا را با متغیرهای a و b مشخص کرده‌ایم. محیط متوازی‌الاضلاعی به ضلع‌های a و b را برابر با متغیر P در نظر می‌گیریم. اکنون، این متغیرها را درون روابط کلامی محیط متوازی‌الاضلاع قرار می‌دهیم:

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

(ضلع دوم × 2) + (ضلع اول × 2) = محیط متوازی‌الاضلاع

$$
P=۲a + ۲b
$$

(ضلع دوم + ضلع اول) × 2 = محیط متوازی‌الاضلاع

$$
P=۲(a + b)
$$

به این ترتیب، عبارت‌های جبری محیط متوازی‌الاضلاع به دست می‌آیند. حروف انتخابی برای نمایش ضلع‌ها یا محیط، اهمیت زیادی ندارد. به عنوان مثال، می‌توانیم به جای متغیر P، از متغیر C به منظور نمایش محیط استفاده کنیم. با این وجود، در اغلب منابع آموزشی، فرمول‌های مختلف ریاضی به یک شکل نوشته می‌شوند. فرمول‌های مختلفی برای محاسبه محیط متوازی‌الاضلاع وجود دارند. در ادامه، به معرفی عبارت‌های جبری این فرمول‌ها می‌پردازیم.

مثال 1: محاسبه محیط متوازی الاضلاع با دو ضلع مجاور

اندازه دو ضلع مجاور در یک متوازی‌الاضلاع، به ترتیب برابر 73 و 68 سانتی‌متر است. محیط متوازی‌الاضلاع را به دست بیاورید.

فرمول محیط متوازی‌الاضلاع به صورت زیر نوشته می‌شود:

$$
P=۲(a + b)
$$

• P: محیط متوازی‌الاضلاع
• a: اندازه یکی از ضلع‌ها برابر 73 سانتی‌متر
• b: اندازه ضلع مجاور a برابر 68 سانتی‌متر

متغیرهای عبارت جبری بالا را با اندازه‌های معلوم آن‌ها جایگزین می‌کنیم:

$$
P=۲ \times (۷۳ + ۶۸)
$$

$$
P=۲ \times (۱۴۱)
$$

$$
P=۲۸۲
$$

در نتیجه، محیط متوازی‌الاضلاع برابر ۲۸۲ سانتی‌متر است. در برخی از مسائل، اندازه‌های مختلف به صورت متغیر داده می‌شوند. در این شرایط، روند حل، تفاوت چندانی با نحوه حل این مثال نخواهد داشت.

مثال 2: محاسبه محیط متوازی الاضلاع به صورت متغیر

تصویر زیر، یک متوازی‌الاضلاع و اندازه بخش‌های مختلف آن را نمایش می‌دهد. مساحت این متوازی‌الاضلاع را حساب کنید. اگر x برابر 20 و y برابر 2 باشد، مقدار عددی مساحت متوازی‌الاضلاع چقدر خواهد بود؟

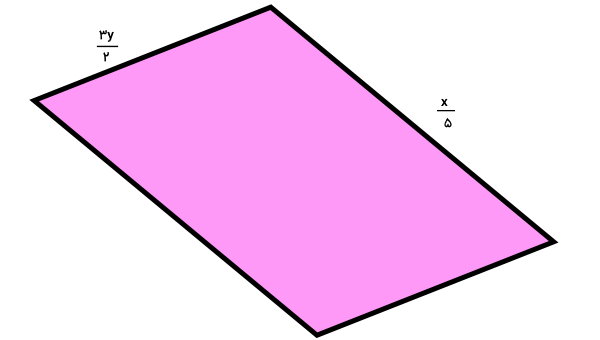
در ریاضیات، هرگاه رابطه بین یک اندازه با اعداد مختلف را داشته باشیم، به جای عدد از متغیر استفاده می‌کنیم. اندازه دو ضلع مجاور متوازی‌الاضلاع بالا، بر حسب متغیرهای x و y نوشته شده‌اند. به منظور محاسبه محیط، ابتدا فرمول آن را می‌نویسیم:

$$
P=۲(a + b)
$$

به جای a و b در فرمول بالا، اندازه‌های آن‌ها را قرار می‌دهیم:

$$
P=۲(\frac {۳y}{۲} + \frac {x}{۵})
$$

فرمول بالا، عبارت جبری محیط متوازی‌الاضلاع بر حسب x و y است. با استفاده از قواعد مخرج مشترک و ضرب کسرها، این فرمول را به فرم زیر تغییر می‌دهیم:

$$
P=۲(\frac {۱۵y}{۱۰} + \frac {۲x}{۱۰})
$$

$$
P=۲(\frac {۱۵y + ۲x}{۱۰})
$$

$$
P=\frac {۳۰y + ۴x}{۱۰}
$$

اگر x برابر 20 و y برابر 2 باشد، مقدار عددی مساحت متوازی‌الاضلاع برابر است با:

$$
P=\frac {(۳۰\times ۲) + (۴ \times ۲۰)}{۱۰}
$$

$$
P=\frac {(۶۰) + (۸۰)}{۱۰}
$$

$$
P=\frac {۱۴۰}{۱۰}
$$

$$
P=۱۴
$$

محیط متوازی الاضلاع با قطر به صورت جبری

قطر، پاره‌خط اتصال‌دهنده گوشه‌های غیر مجاور یک شکل هندسی است. تصویر زیر، قطرهای متوازی‌الاضلاع را نمایش می‌‌دهد.

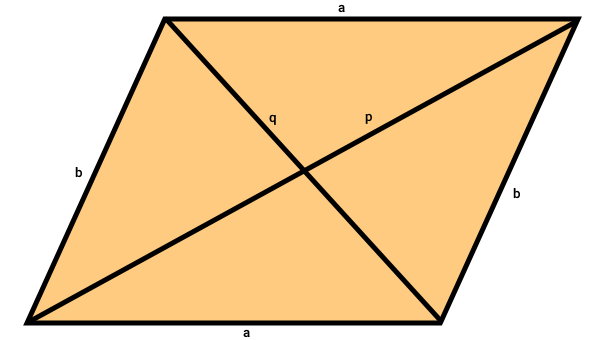
در این متوازی‌الاضلاع، اندازه‌های قطرها، با حروف p و q مشخص شده‌اند. اگر این دو اندازه و اندازه یکی از ضلع‌های a یا b را داشته باشیم، فرمول محیط متوازی الاضلاع به صورت جبری را می‌نویسیم:

فیلم آموزش هندسه پایه دهم – هندسه ۱ در فرادرس

کلیک کنید

$$
P = ۲a +\sqrt{۲p^۲+۲q^۲-۴a^۲}
$$

یا

$$
P = ۲b +\sqrt{۲p^۲+۲q^۲-۴b^۲}
$$

مثال 3: محاسبه محیط متوازی الاضلاع با قطر

اندازه یک ضلع و قطرهای متوازی‌الاضلاعی به ترتیب برابر 8، 23 و 19 متر است. محیط این متوازی‌الاضلاع را به دست بیاورید.

به منظور تعیین محیط یک متوازی‌الاضلاع با قطر، از فرمول زیر استفاده می‌کنیم:

$$
P = ۲a +\sqrt{۲p^۲+۲q^۲-۴a^۲}
$$

• P: محیط متوازی الاضلاع
• a: اندازه یکی از ضلع‌ها برابر 8 متر
• p: اندازه یکی از قطرها برابر 23 متر
• q: اندازه قطر دیگر برابر 19 متر

$$
P = (۲ \times ۸) +\sqrt{(۲ \times ۲۳^۲) + (۲ \times ۱۹^۲ ) - (۴ \times ۸^۲)}
$$

$$
P = (۱۶) +\sqrt{(۲ \times ۵۲۹) + (۲ \times ۴۳۷ ) - (۴ \times ۶۴)}
$$

$$
P = (۱۶) +\sqrt{(۱۰۵۸) + (۷۲۲) - (۲۵۶)}
$$

$$
P = (۱۶) +\sqrt{۱۵۲۴}
$$

$$
P = (۱۶) + ۳۹/۰۴
$$

$$
P = ۵۵/۰۴
$$

در نتیجه، محیط متوازی‌الاضلاع برابر ۵۵/۰۴ متر است.

محیط متوازی الاضلاع با قاعده و ارتفاع به صورت جبری

ضلع پایینی متوازی‌الاضلاع، معمولا با عنوان «قاعده» شناخته می‌شود. البته در صورت مشخص بودن ارتفاع نظیر ضلع‌های متوازی‌الاضلاع، می‌توانیم هر یک از ضلع‌ها را به عنوان قاعده در نظر بگیریم. ارتفاع نظیر یک ضلع، فاصله عمودی بین آن با ضلع مقابلش است. تصویر زیر، نمونه‌ای از ارتفاع و قاعده نظیر در یک متوازی‌الاضلاع را نمایش می‌دهد.

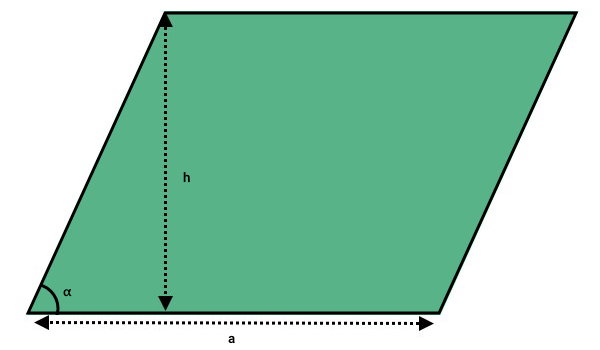
اندازه قاعده متوازی‌الاضلاع را با حرف a، اندازه ارتفاع آن را با حرف h و اندازه زاویه بین دو ضلع مجاور آن را با حرف α مشخص کرده‌ایم. بر اساس این متغیرها، محیط متوازی الاضلاع به صورت جبری برابر است با:

فیلم آموزش هندسه ۳ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

$$
P =۲a + \frac {۲h} {\sin {\alpha}}
$$

مثال 4: محاسبه محیط متوازی الاضلاع با ارتفاع

محیط متوازی‌الاضلاع زیر را به دست بیاورید. (سینوس زاویه 40 درجه را برابر 0/64 در نظر بگیرید.)

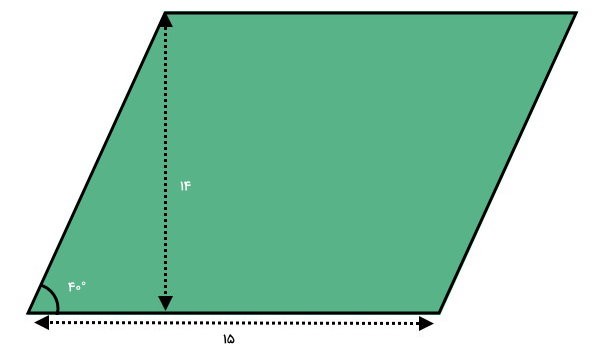
تصویر بالا، اندازه قاعده متوازی‌الاضلاع، ارتفاع نظیر آن و یکی از زاویه‌ها را نمایش می‌دهد. بر اساس این اطلاعات، محیط متوازی‌الاضلاع به کمک رابطه زیر قابل محاسبه است:

$$
P =۲a + \frac {۲h} {\sin {\alpha}}
$$

• P: محیط متوازی‌الاضلاع
• a: قاعده برابر 15
• h: ارتفاع برابر 14
• α: یکی از زاویه‌ها برابر 40 درجه

$$
P =۲a + \frac {۲h} {\sin {\alpha}}
$$

$$
P = (۲ \times ۱۵) + \frac {۲ \times ۱۴} {\sin {۴۰^{\circ}}}
$$

$$
P = (۳۰) + \frac {۲۸} {۰/۶۴}
$$

$$
P = ۳۰ + ۴۳/۷۵
$$

$$
P = ۷۳/۷۵
$$

محیط متوازی الاضلاع با مساحت به صورت جبری

مساحت متوازی‌الاضلاع، سطح میان ضلع‌های آن است. فرمول مساحت متوازی‌الاضلاع به صورت زیر نوشته می‌شود:

فیلم مجموعه آموزش دروس پایه هشتم – درس، تمرین، حل مثال و تست در فرادرس

کلیک کنید

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

در اغلب منابع، مساحت شکل‌های هندسی با حرف A یا S نمایش داده می‌شود. به این ترتیب، مساحت متوازی‌الاضلاع به صورت جبری عبارت است از:

$$
A = b h
$$

بر اساس عبارت جبری بالا، می‌توانیم اندازه هر ضلع متوازی‌الاضلاع را بر حسب مساحت و ارتفاع نظیر به دست بیاوریم:

$$
b = \frac {A} {h}
$$

اگر رابطه بالا را درون فرمول محیط متوازی‌الاضلاع با ضلع قرار دهیم، به عبارت جبری محیط متوازی الاضلاع با مساحت می‌رسیم:

$$
P=۲ a+۲ \frac{A}{h}
$$

مثال 5: محاسبه محیط متوازی الاضلاع از روی مساحت

مساحت یک متوازی‌الاضلاع برابر 1440 میلی‌متر مربع است. اگر اندازه یکی از ضلع‌ها برابر 41 میلی‌متر و ارتفاع نظیر آن برابر 35 میلی‌متر باشد، محیط متوازی‌الاضلاع، چقدر است؟

بر اساس فرمول محیط متوازی الاضلاع با مساحت داریم:

$$
P=۲ a+۲ \frac{A}{h}
$$

• P: محیط متوازی‌الاضلاع
• a: اندازه یکی از ضلع‌ها برابر 41 میلی‌متر
• A: مساحت متوازی‌الاضلاع برابر 1440 میلی‌متر مربع
• h: ارتفاع نظیر a برابر 35 میلی‌متر

$$
P= (۲ \times ۴۱) + \frac{۲ \times ۱۴۴۰}{۳۵}
$$

$$
P= (۸۲) + \frac{۲۸۸۰}{۳۵}
$$

$$
P= ۸۲ + ۸۲/۲۹
$$

$$
P= ۱۶۴/۲۹
$$