چند ضلعی مقعر چیست؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده

چند ضلعی مقعر خط بستهای است که از حداقل یک راس با زاویه داخلی بزرگتر از ۱۸۰ درجه تشکیل میشود. در این مقاله، ابتدا به معرفی اجزای چند ضلعی های مقعر و روشهای تشخیص این نوع از چندضلعیهای میپردازیم. سپس، فرمولهای محاسبه زاویههای داخلی و خارجی چندضلعیهای مقعر را به همراه حل چندین مثال متنوع ارائه میکنیم.
چند ضلعی چیست و چه انواعی دارد؟
چندضلعی، مجموعهای از پارهخطهای بهمپیوسته و بسته است. این نوع از اشکال هندسی، بر اساس اندازه زاویههای داخلی به دو نوع محدب و مقعر تقسیم میشوند.
اگر طول ضلعها با هم و اندازه زاویهها با هم برابر باشند، چندضلعی، از نوع منتظم بوده و در غیر اینصورت، غیرمنتظم است. تصویر زیر، یک چندضلعی محدب و یک چند ضلعی مقعر را نمایش میدهد.
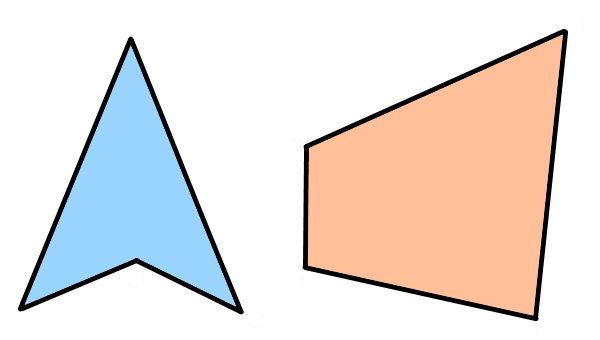
چند ضلعی مقعر چیست؟
به چندضلعیهایی که حداقل یک زاویه بزرگتر از ۱۸۰ دارند، چند ضلعی مقعر میگویند. چندضلعی مقعر با عنوان چند ضلعی کاو نیز شناخته میشود. چند نمونه چند ضلعی مقعر را میتوانید در تصویر زیر مشاهده کنید.
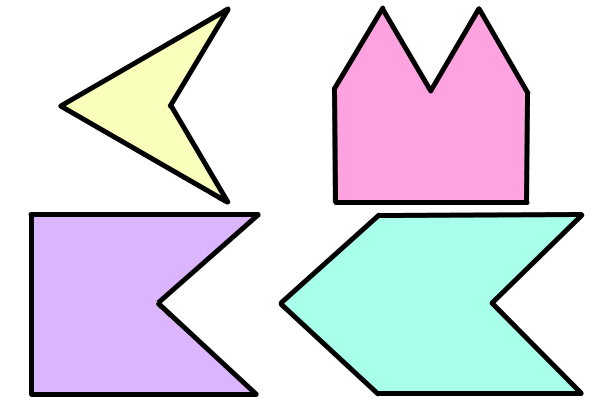
تمام چندضلعیهای بالا، حداقل یک زاویه بزرگتر از ۱۸۰ درجه دارند. در ادامه، نحوه تشخیص این زاویهها و تعیین مقعر بودن چندضلعیها را آموزش میدهیم.
روش های تشخیص چند ضلعی مقعر
اگر یکی از حالتهای زیر در یک چندضلعی قابل مشاهده باشد، آن چندضلعی، مقعر در نظر گرفته میشود:
- وجود زاویه داخلی بزرگتر از ۱۸۰ درجه
- قرارگیری امتداد ضلعها درون شکل
- قطع ضلعها توسط خط واصل هر دو نقطه دلخواه درون شکل
تشخیص چندضلعی مقعر با استفاده از زاویه داخلی
انواع زاویههای داخلی یک چندضلعی عبارت هستند از:
- زاویه حاده: زاویه کوچکتر از ۹۰ درجه
- زاویه منفرجه: زاویه بزرگتر از ۹۰ درجه
- زاویه قائمه یا زاویه راست: زاویه ۹۰ درجه
- زاویه مقعر یا زاویه کاو: زاویه بزرگتر از ۱۸۰ درجه
همانطور که از اسم زوایههای بالا مشخص است، وجود زاویه داخلی بزرگتر از ۱۸۰ درجه، نشاندهنده مقعر بودن چندضلعیها است. تشخیص این زاویهها، معمولا کار دشواری نبوده و با چشم نیز قابل انجام است.
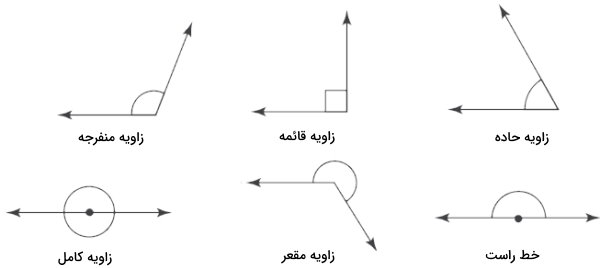
نکته: به خاطر داشته باشید که در چندضلعیها، هیچ زاویهای نمیتواند برابر با ۱۸۰ درجه (زاویه نیمصفحه) یا 360 درجه (زاویه کامل) باشد.
مثال ۱: تعیین نوع چندضلعی با زاویههای معلوم
تصویر زیر، یک چهارضلعی را نمایش میدهد. با توجه به زاویههای این چهارضلعی، نوع آن را مشخص کنید.
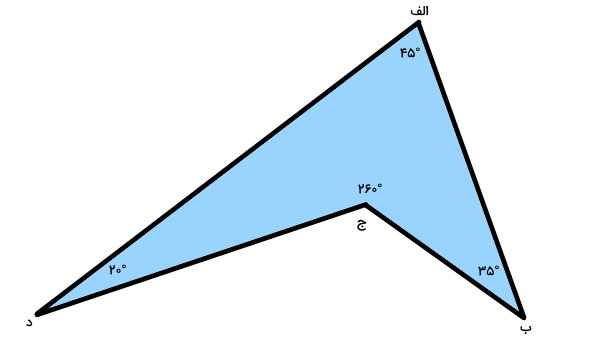
زاویههای چهارضلعی (الف ب ج د) برابر هستند با:
۱۸۰° > ۴۵° = زاویه راس الف
۱۸۰° > ۳۵° = زاویه راس ب
۱۸۰° < ۲۶۰° = زاویه راس ج
۱۸۰° > ۲۰° = زاویه راس د
راس ج، از ۱۸۰ درجه بزرگتر است. بنابراین، به دلیل وجود حداقل یک زاویه بزرگتر از ۱۸۰ درجه، چهارضلعی (الف ب ج د)، یک چندضلعی مقعر محسوب میشود.
تشخیص چندضلعی مقعر با امتداد ضلعها
با امتداد دادن ضلعهای یک چندضلعی، یکی از دو حالت زیر به وجود میآید:
- امتداد ضلع، خارج از محدوده چندضلعی قرار میگیرد.
- امتداد ضلع، از داخل چندضلعی عبور میکند.
در تصویر زیر، تمام امتدادهای چندضلعی سمت راست، خارج از محدوده آن قرار دارد. پس این چندضلعی نمیتواند مقعر باشد. در طرف مقابل، امتداد دو ضلعِ چندضلعی سمت چپ، درون آن قرار گرفته است. بنابراین، این شکل، یک چند ضلعی مقعر محسوب میشود.
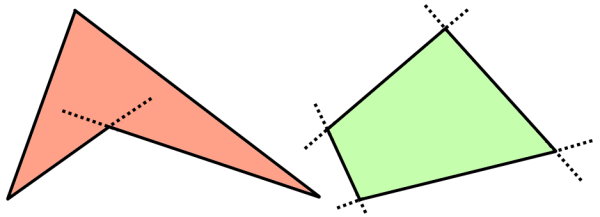
برای تایید مقعر بودن یک چندضلعی، نیازی به رسم امتداد تمام ضلعها نیست. همین که فقط یکی از امتدادها درون شکل قرار بگیرید، نشانه مقعر بودن آن است.
مثال ۲: تعیین نوع چندضلعی با زاویههای مجهول
آیا پنجضلعی زیر، مقعر است؟
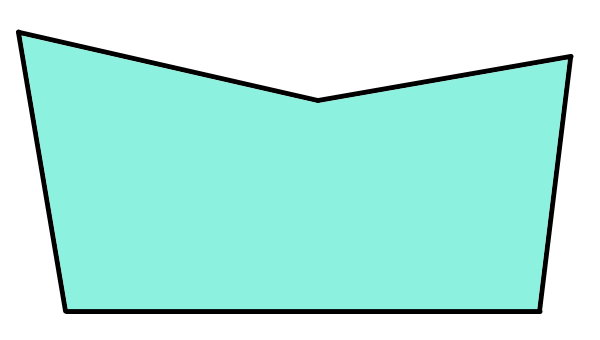
به منظور تشخیص مقعر بودن یا نبودن شکل بالا، امتداد ضلعها را از دو طرف رسم میکنیم. با قرارگیری حداقل یک امتداد در درون شکل، مقعر بودن آن تایید میشود. در غیر اینصورت، مقعر بودن شکل رد خواهد شد.
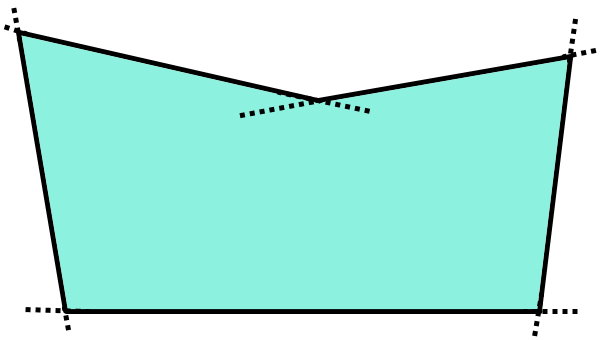
همانطور که مشاهده میکنید، امتدادهای دو ضلع بالایی، درون شکل قرار میگیرند. بنابراین، جواب سوال مثبت بوده و چندضلعی بالا، مقعر است.
تشخیص چندضلعی مقعر با اتصال دو نقطه
اگر دو نقطه درون یک چندضلعی را بهم وصل کنیم، یکی از حالتهای زیر رخ میدهد:
- خط اتصال دو نقطه، به طور کامل درون شکل قرار میگیرد.
- خط اتصال دو نقطه، ضلعها را قطع میکنند.
یک چندضلعی مقعر است؛ اگر دو نقطه در آن وجود داشته باشند که خط اتصالشان، ضلعهای چندضلعی را قطع کند. سادهترین راه برای استفاده از این روش، اتصال نقاط نزدیک به گوشههای شکل است.
مثال ۳: تعیین نوع چندضلعی با اتصال نقاط
شکل زیر، یک چندضلعی مقعر است. مقعر بودن این چندضلعی را با استفاده از روش اتصال نقاط داخلی اثبات کنید.

اگر بتوانیم دو نقطه را پیدا کنیم که خط اتصالشان، حداقل یکی از ضلعهای چندضلعی را قطع کنند، مقعر بودن چندضلعی اثبات میشود. به این منظور، چند نقطه را در نزدیکی گوشههای شکل رسم کرده و آنها را به هم وصل میکنیم.
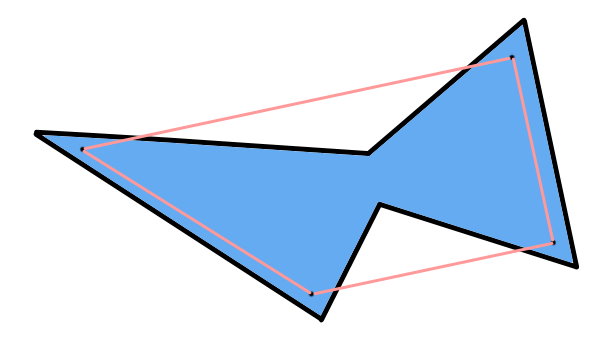
برخی از خطوط اتصال نقاط داخلی چندضلعی، ضلعهای آن را قطع کردهاند. بنابراین، چندضلعی بالا، از نوع مقعر است.
زاویه داخلی چند ضلعی مقعر چیست؟
به زاویههایی که در گوشههای چندضلعی تشکیل میشوند و درون آن قرار میگیرند، زاویه داخلی میگویند.
چندضلعی مقعر، حداقل یک زاویه داخلی بزرگتر از ۱۸۰ درجه دارد.
مجموع زوایای داخلی چند ضلعی مقعر
مجموع زوایای داخلی هر چندضلعی مقعر، بر اساس تعداد ضلعهای آن محاسبه میشود. فرمول مجموع زوایای داخلی تمام چندضلعیها عبارت است از:
- S: مجموع زوایای داخلی چندضلعی مقعر
- n: تعداد ضلعهای چندضلعی مقعر
مثال ۴: محاسبه مجموع زاویه های داخلی چندضلعی مقعر
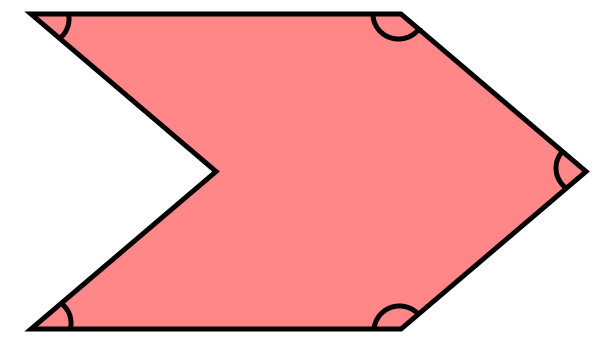
نوع چندضلعی زیر تعیین کنید. سپس، مجموع زوایای داخلی آن را به دست بیاورید.
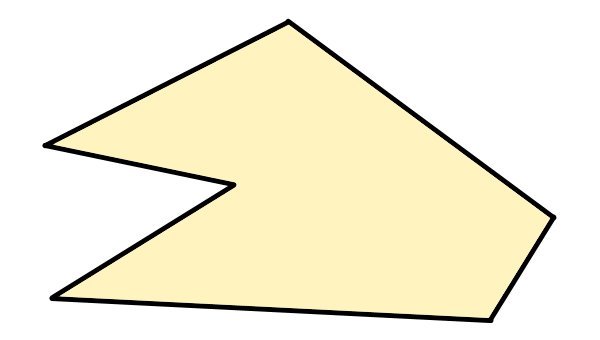
چندضلعی بالا مقعر است. یکی از راسهای این چندضلعی، به وضوح، زاویهای بزرگتر از ۱۸۰ درجه دارد. امتداد ضلعهای این راس، درون چندضلعی قرار میگیرند. به علاوه، دو نقطه را میتوان رسم کرد که ضلعهای آن را قطع کنند.
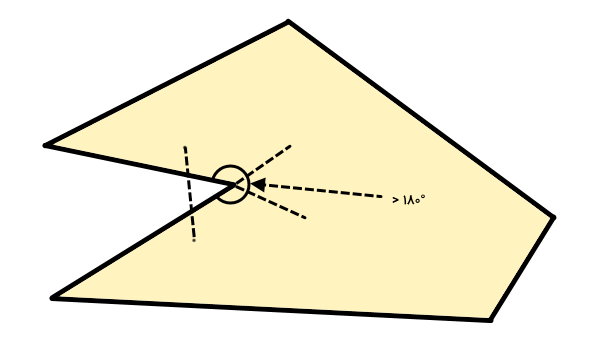
تعداد ضلعهای چندضلعی مقعر بالا برابر با ۶ است. بنابراین، مجموع زاویههای داخلی آن از رابطه زیر محاسبه میشود:
- S: مجموع زوایای داخلی چندضلعی مقعر
- n: تعداد ضلعهای چندضلعی مقعر برابر ۶
در نتیجه، مجموع زاویههای داخلی ششضلعی مقعر برابر با ۷۲۰ درجه است.
مثال ۵: محاسبه یکی از زاویههای چندضلعی مقعر
مجموع هفت زاویه داخلی یک هشتضلعی برابر با ۸۷۰ درجه است. زاویه هفتم و نوع این هشتضلعی را تعیین کنید.
مجموع زاویههای داخلی چندضلعی مورد سوال برابر است با:
زاویه هشتم + مجموع هفت زاویه = مجموع تمام زاویهها
بنابراین، زاویه هشتم چندضلعی از رابطه زیر به دست میآید:
مجموع هفت زاویه - مجموع تمام زاویهها = زاویه هشتم
جمع تمام زاویههای داخلی چندضلعی، به صورت زیر محاسبه میشود:
- S: مجموع زوایای داخلی چندضلعی
- n: تعداد ضلعهای چندضلعی برابر ۸
به این ترتیب، داریم:
۸۷۰° - ۱۰۸۰° = زاویه هشتم
۲۱۰° = زاویه هشتم
زاویه هشتم ششضلعی برابر با ۲۱۰ درجه است. این ششضلعی، یک زاویه بزرگتر از ۱۸۰ درجه دارد و به عنوان یک ششضلعی مقعر در نظر گرفته میشود.
تعیین حداقل تعداد ضلعهای چندضلعی مقعر
یک سهضلعی را در نظر بگیرید. مجموع زوایای داخلی این سهضلعی، برابر است با:
در یک چندضلعی مقعر، باید حداقل یک زاویه داخلی بزرگتر از ۱۸۰ درجه وجود داشته باشد. با توجه به رابطه بالا، وجود حتی یک زاویه داخلی بزرگتر از ۱۸۰ درجه برای یک سهضلعی امکانپذیر نیست. اکنون، یک چهارضلعی را در نظر بگیرید. مجموع زوایای داخلی چهارضلعی برابر است با:
با توجه به عدد به دست آمده، وجود یک زاویه داخلی بزرگتر از ۱۸۰ درجه امکانپذیر است. بنابراین، یک چندضلعی مقعر، حداقل باید ۴ ضلع داشته باشد.
زاویه خارجی چند ضلعی مقعر چیست؟
به زاویه بین یک ضلع و امتداد ضلع مجاور آن، زاویه خارجی میگویند. مجموع هر زاویه خارجی با زاویه داخلی مجاور آن، برابر با ۱۸۰ درجه است. تصویر زیر، زاویه داخلی و زاویه خارجی در یک چندضلعی مقعر را نمایش میدهد.
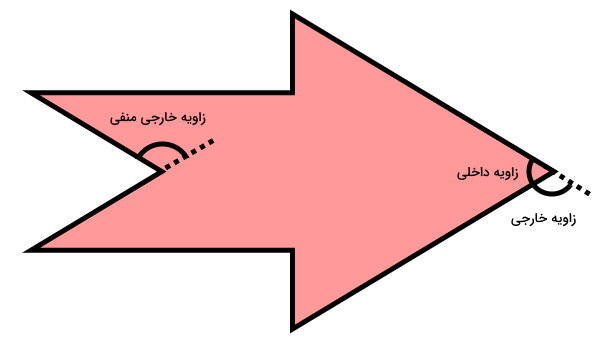
وجه تمایز زاویه خارجی چندضلعی مقعر با دیگر چندضلعیها، امکان منفی شدن این زاویه است. زاویه خارجی مجاور راسهای بزرگتر از ۱۸۰ درجه، مقدار منفی دارد.
مجموع زوایای خارجی چندضلعی مقعر
جمع زاویههای خارجی چندضلعی مقعر، همواره برابر با ۳۶۰ درجه است. به عبارت دیگر، برخلاف رابطه مجموع زاویههای داخلی، تعداد ضلعها، تاثیری بر روی مجموع زاویههای خارجی چندضلعی مقعر ندارد.
چندضلعی مقعر زیر و زاویههای داخلی و خارجی آن را در نظر بگیرید.
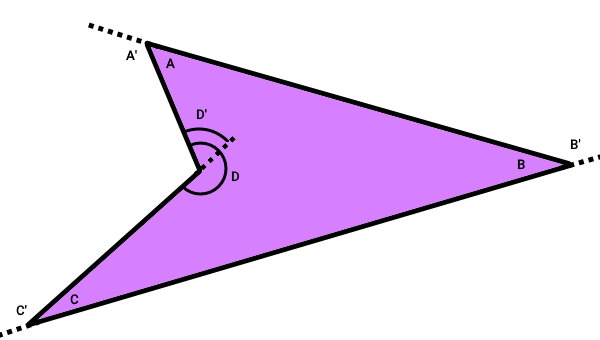
مجموع زوایای داخلی و خارجی این چندضلعی مقعر برابر است با:
جمع هر زاویه داخلی با زاویه خارجی مجاورش، برابر با ۱۸۰ درجه میشود:
به عبارت دیگر:
زاویههای داخلی را در کنار یکدیگر و زاویههای داخلی را در کنار یکدیگر مینویسیم:
با استفاده از فرمول زیر، مجموع زوایای داخلی چندضلعی (در اینجا چهارضلعی) مقعر را بدست میآوریم:
- S: مجموع زوایای داخلی
- n: تعداد ضلعها برابر ۴
مقدار بدست آمده را در رابطه جمع تمام زاویهها قرار میدهیم:
همانطور که مشاهده میکنید. مجموع زوایای خارجی چندضلعی مقعر، برابر با ۳۶۰ درجه شد. در اینجا، مجموع زوایای داخلی یک چهارضلعی مقعر را مورد بررسی قرار دادیم. اگر این محاسبات را برای پنجضلعی، ششضلعی یا دیگر انواع چندضلعی مقعر با تعداد ضلعهای دلخواه تعیین کنیم، نتیجه محاسبات یکسان خواهد بود. در رابطه با مجموع زوایای داخلی و خارجی انواع چندضلعیها، چندین مطلب در مجله فرادرس تهیه شده است که مطالعه آنها را به شما پیشنهاد میکنیم:
- مجموع زوایای چندضلعی مقعر — به زبان ساده + حل تمرین و اثبات فرمول
- مجموع زوایای داخلی چندضلعی محدب چیست؟ — به زبان ساده + حل مثال
- مجموع زوایای خارجی چندضلعی محدب چیست؟ — به زبان ساده + حل مثال
- مجموع زوایای خارجی چندضلعی منتظم — به زبان ساده + اثبات
قطر چند ضلعی مقعر چیست؟
قطر، پارهخطی است که از اتصال راس یا گوشههای غیر مجاور یک چندضلعی ایجاد میشود. در چندضلعیهای مقعر، حداقل یکی از قطرها، به طور کامل خارج از شکل قرار میگیرند. این ویژگی، یکی دیگر از روشهای تشخیص مقعر بودن چندضلعیها است.
فرمول تعداد قطرهای چندضلعی مقعر
تعداد قطرهای هر چندضلعی مقعر از فرمول زیر به دست میآید:
- d: تعداد قطرها
- n: تعداد ضلعها یا راسها
مثال ۶: محاسبه تعداد قطرهای چندضلعی مقعر
پنجضلعی مقعر، چند قطر دارد؟
قطرهای یک پنجضلعی مقعر برابر است با:
- d: تعداد قطرها
- n: تعداد ضلعها برابر ۵
در نتیجه، یک پنجضلعی مقعر، ۵ قطر دارد.
مثال ۷: تعیین نوع چندضلعی با رسم قطرها
پس از رسم قطرهای چندضلعی زیر، نوع آن را مشخص کنید.
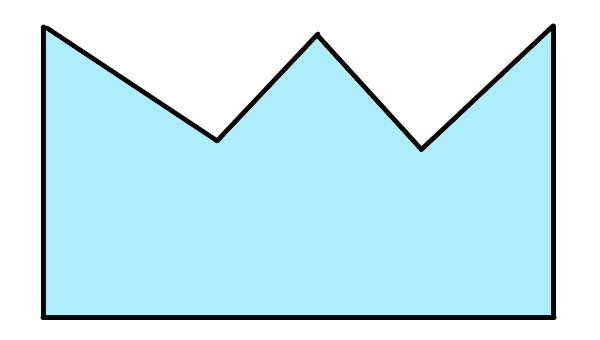
به منظور رسم قطرهای چندضلعی بالا، راسهای غیر مجاور آن را به یکدیگر وصل میکنیم.
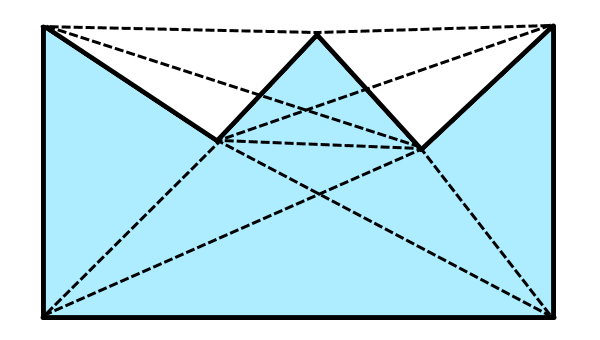
چند قطر، ضلعهای چندضلعی را قطع کردهاند. به علاوه، چند قطر نیز بیرون از محدوده ضلعها قرار گرفتهاند. بنابراین، چندضلعی بالا، از نوع مقعر است.
آیا چند ضلعی مقعر منتظم وجود دارد ؟
چندضلعی منتظم، دارای ضلعهای مساوی و زاویههای هماندازه است. به عبارت دیگر، هیچیک از ضلعها و هیچیک از زاویههای چندضلعی منتظم، از نظر اندازه با یکدیگر تفاوتی ندارند. بر اساس تعریفهای ارائه شده، چندضلعی مقعر، از حداقل یک زاویه داخلی بزرگتر از ۱۸۰ درجه تشکیل میشود. از طرف دیگر، مجموع زوایای داخلی هر چندضلعی مقعر برابر با °۱۸۰ × (۲ - n) است.
اگر تعریف چندضلعی مقعر را با فرمول مجموع زاویههای آن مقایسه کنیم، در مییابیم که این نوع چندضلعی، به هیچ وجه نمیتواند منتظم شود. به عنوان مثال، مجموع زاویههای داخلی یک چهارضلعی مقعر برابر با ۳۶۰ درجه است. در صورت منتظم بودن این چهارضلعی، اندازه زاویه هر راس آن باید برابر با مقدار زیر باشد:
۹۰° = ۴ ÷ ۳۶۰°
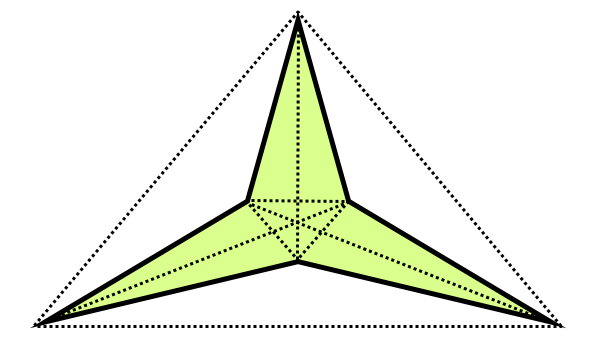
تمام زاویههای چهارضلعی منتظم برابر با ۹۰ درجه و کوچکتر از ۱۸۰ درجه است. در نتیجه، چهارضلعی منتظم نمیتواند مقعر باشد. این موضوع برای دیگر چندضلعیهای منتظم نیز صدق میکند. البته، برخی از افراد، چندضلعیهای ستارهای شکل را با چندضلعیهای منتظم اشتباه میگیرند. تصویر زیر، نمونهای از یک چندضلعی ستارهای را نمایش میدهد.

چندضلعی ستارهای، شکلی با ضلعهای برابر است. البته، به دلیل هماندازه نبودن تمام زاویههای داخلی، این شکل، منتظم نیست. علاوه بر این، به دلیل وجود زاویههای بزرگتر از ۱۸۰ درجه، شکلهای ستارهای، به عنوان چندضلعیهای مقعر در نظر گرفته میشوند.
محیط و مساحت چند ضلعی مقعر چگونه بدست می آید؟
محیط چندضلعی مقعر، با جمه طول تمام ضلعهای آن به دست میآید. برخلاف چندضلعیهای منتظم و برخی از چندضلعیهای محدب، فرمول سادهای برای تعیین مساحت چندضلعیهای مقعر وجود ندارد. یکی از روشهای رایج برای انجام این محاسبات، تبدیل چندضلعی به چندین مثلث است. در این روش، با رسم قطرهای داخل چندضلعی مقعر، آن را به چندین مثلث تبدیل میکند. جمع مساحت مثلثها، مساحت چندضلعی مقعر است.
تفاوت چند ضلعی مقعر با چند ضلعی محدب چیست؟
چند ضلعی محدب، یکی از انواع چندضلعیهای است که تمام زاویههای آن کوچکتر از ۱۸۰ درجه هستند.
جدول زیر، تفاوتهای چندضلعیهای محدب و مقعر را نمایش میدهد.
| چندضلعی مقعر | چندضلعی محدب |
| دارای حداقل یک زاویه بزرگتر از ۱۸۰ درجه | بدون زاویه بزرگتر از ۱۸۰ درجه |
| دارای حداقل ۴ ضلع | دارای حداقل ۳ ضلع |
| قرارگیری حداقل یک قطر در خارج از شکل | قرارگیری تمام قطرها درون شکل |
| عبور امتداد برخی از ضلعها از درون شکل | قرارگیری امتداد تمام ضلع در خارج از شکل |
| منفی بودن حداقل یکی از زاویههای خارجی | مثبت بودن تمام زاویههای خارجی |
با وجود تفاوتهای بین چندضلعیهای محدب و مقعر، مجموع زوایای داخلی این دو نوع چندضلعی و تعداد قطرهای آنها، با استفاده از فرمولهای یکسان تعیین میشوند. به علاوه، جمع زوایای خارجی در هر دو چندضلعی مقعر و محدب، برابر با ۳۶۰ درجه است.
ترکیب چندضلعیهای محدب و مقعر
از ترکیب چندضلعیهای مقعر و محدب با یکدیگر، چندضلعیهای جدید به وجود میآیند. شکل حاصل از ترکیب چندضلعیها میتواند محدب یا مقعر باشد. به عبارت دیگر:
- از ترکیب دو چند ضلعی مقعر میتوان یک چند ضلعی محدب ساخت.
- از ترکیب دو چند ضلعی مقعر، میتوان یک چند ضلعی مقعر ساخت.
- از ترکیب دو چند ضلعی محدب، میتوان یک چند ضلعی مقعر ساخت.
- از ترکیب دو چند ضلعی محدب، میتوان یک چند ضلعی محدب ساخت.
- از ترکیب یک چند ضلعی محدب با یک چند ضلعی مقعر، میتوان یک چند ضلعی محدب ساخت.
- از ترکیب یک چند ضلعی محدب با یک چند ضلعی مقعر، میتوان یک چند ضلعی مقعر ساخت.
سوالات متداول در رابطه با چند ضلعی مقعر
در این بخش، به برخی از سوالات پرتکرار در رابطه با چندضلعیهای مقعر و ویژگیهای آنها به طور خلاصه پاسخ میدهیم.
تعریف چند ضلعی مقعر چیست؟
به چندضلعیهایی که حداقل یک زاویه بزرگتر از ۱۸۰ درجه دارند، چندضلعی مقعر گفته میشود.
انواع چند ضلعی مقعر چه هستند؟
انواع چندضلعی مقعر بر اساس تعداد ضلعها، عبارت از چهارضلعی، پنجضلعی، ششضلعی و غیره هستند.
آیا چند ضلعی های مقعر منتظم هستند؟
خیر. با توجه به تعریف چندضلعی منتظم و فرمول مجموع زوایای داخلی چندضلعیها، هیچیک از انواع چندضلعیهای مقعر، منتظم نیستند.
آیا ذوزنقه یک چند ضلعی مقعر است ؟
خیر. ذوزنقه، هیچ زاویه داخلی بزرگتر از ۱۸۰ درجه ندارد.
یک چند ضلعی مقعر حداقل چند ضلع دارد؟
یک چند ضلعی مقعر، حداقل ۴ ضلع دارد.
کوچکترین چند ضلعی مقعر چیست؟
چهارضلعی مقعر، کوچکترین چندضلعی مقعر است.
فرق چند ضلعی محدب و مقعر چیست؟
فرق چندضلعی مقعر و محدب، عدم وجود حداقل یک زاویه داخلی بزرگتر از ۱۸۰ درجه در چندضلعی محدب است.
آیا شکل ستاره مقعر است؟
بله. تمام چندضلعیهای ستارهای، مقعر هستند.
آیا یک چندضلعی می تواند هم مقعر و هم محدب باشد؟
خیر.
از چسباندن چندضلعی مقعر و محدب چه شکلی می توان ساخت؟
از چسباندن چندضلعی مقعر و محدب میتوان چندضلعی مقعر یا محدب ساخت.
جمع زاویه های داخلی چند ضلعی مقعر چند است؟
جمع زوایای داخلی چندضلعیهای مقعر، برابر با «°۱۸۰ × (۲ - تعداد ضلعها)» است.
جمع زاویه های خارجی چند ضلعی مقعر چند است؟
جمع زوایای خارجی چندضلعیهای مقعر برابر با ۳۶۰ درجه است.
چند ضلعی مقعر چند قطر دارد؟
هر چندضلعی مقعر، «۲ ÷ (۲ - n)n» قطر دارد. n، تعداد ضلعهای چندضلعی است. >۱۸۰°
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش انواع چند ضلعی ها — تعاریف و تمامی فرمول های محیط و مساحت» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- چند ضلعی چیست ؟ — به زبان ساده
- چند ضلعی محدب چیست ؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده
- چند ضلعی مقعر چیست ؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده(همین مطلب)
- چند ضلعی منتظم چیست ؟ — به زبان ساده + فیلم آموزش رایگان و حل تمرین
- مجموع زوایای داخلی چند ضلعی محدب چیست ؟ — به زبان ساده + حل مثال
- مجموع زوایای خارجی چند ضلعی محدب چیست ؟ — به زبان ساده + حل مثال
- فرمول بدست آوردن مجموع زوایای داخلی چند ضلعی + حل تمرین
- مجموع زوایای چند ضلعی مقعر — به زبان ساده + حل تمرین و اثبات فرمول
- مجموع زوایای خارجی چند ضلعی منتظم — به زبان ساده + اثبات
- مساحت چند ضلعی منتظم چگونه بدست می آید ؟ — به زبان ساده + حل مثال
- محور تقارن چند ضلعی منتظم چیست ؟ — به زبان ساده












