چهار ضلعی ها در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

پیشتر در وبلاگ فرادرس مباحث مختلف مربوط به هندسه مورد بررسی قرار گرفت. از جمله این مطالب میتوان به مطلب «چندضلعی و تعریف آن در هندسه» از مجله فرادرس اشاره کرد که به بررسی چندضلعیها پرداخته است. همانطور که در این مطالب اشاره شد، پرکاربردترین اشکال موجود در هندسه، چهار ضلعیها هستند که از اشکالی مانند مربع، مستطیل، لوزی، کایت یا شبه لوزی، متوازی الاضلاع و ذوزنقه تشکیل میشوند. این مطلب به بررسی و تعریف چهار ضلعی و معرفی انواع آنها میپردازد. همچنین ویژگی چهار ضلعیهای مختلف به صورت دقیق مورد ارزیابی قرار میگیرد.
فیلم آموزشی چهار ضلعی ها
به صورت کلی میتوان بیان کرد که یک چهار ضلعی یا کوادریلاترال، جسمی در نظر گرفته میشود که از چهار وجه یا ضلع تشکیل شده است.
نکته مهم دیگری که باید به آن توجه کرد این است که چهار ضلعی یک هندسه دو بعدی بسته و شامل چهار ضلع است که اضلاع یا وجوه آن به صورت خطوط مستقیم هستند. شکل زیر چند نمونه از انواع مختلف چهار ضلعیها را به تصویر کشیده است.
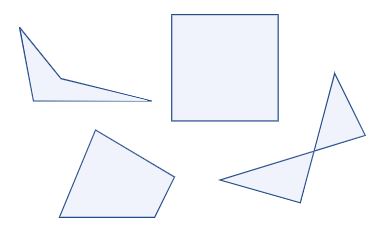
زمانی که از چند ضلعی و هندسه سخن به میان میآید، مفاهیمی چون راس، یال و وجه اهمیت بسیار زیادی پیدا میکنند و این مفاهیم در اکثر مسائل کاربرد دارند. بنابراین این مطلب در ابتدا به صورت دقیق به بررسی این سه مفهوم در هندسه میپردازد.
برای بیان یک تعریف مناسب از راس، یال و وجه به شکل زیر توجه کنید.
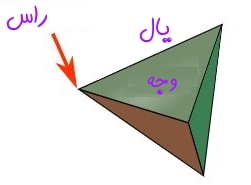
راس، یکی از گوشههای شکل نشان داده شده را نمایش میدهد و یال، خطی است که دو راس این شکل هندسی را به یکدیگر متصل میکند. همچنین وجه نیز یک صفحه مشخص در نظر گرفته میشود که مانند شکل توسط چند یال احاطه شده است.
خواص چهار ضلعی
در ابتدای این مطلب تعریف چهار ضلعی مورد بررسی قرار گرفت و بیان شد که چهار ضلعی از چهار وجه یا ضلع تشکیل میشود. بنابراین یکی از مهمترین خواص چهار ضلعی و مشخصه اصلی آنها همین مسئله است.
مشخصه دوم چهار ضلعیها این است که آنها از چهار راس یا گوشه تشکیل شدهاند. این ویژگی را میتوان با دقت به شکل چهار ضلعیهای معروفی مانند مربع که با آن آشنا هستید نیز به خوبی متوجه شوید.

در نهایت خاصیت و ویژگی سوم چهار ضلعیها این است که مجموع زوایای داخلی آنها برابر با 360 درجه است. برای مثال دو چهار ضلعی به همراه زوایای داخلی آنها در شکل زیر نشان داده شدهاند.
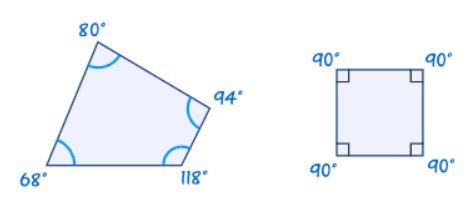
شکل سمت راست بالا یک مربع را نشان میدهد که تمام زوایای داخلی آن برابر با 90 درجه است. بنابراین مجموع این زوایای داخلی را میتوان با استفاده از رابطه زیر محاسبه کرد.
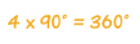
همچنین شکل سمت چپ یک چهار ضلعی دلخواه را به تصویر کشده است. با دقت به زوایای نشان داده شده در شکل متوجه میشویم که مجموع این زوایای داخلی نیز برابر با 360 درجه است که جمع آنها با استفاده از رابطه زیر نشان داده شده است.
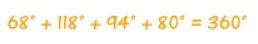
شما میتوانید خودتان یک چهار ضلعی دلخواه را رسم و زوایای داخلی آن را با دقت اندازهگیری کنید. با جمع زوایای اندازهگیری شده متوجه خواهید شد که مجموع آنها برابر با مقدار ثابت 360 درجه است.
انواع چهار ضلعی
در این قسمت انواع مختلف چهار ضلعیها مورد بررسی قرار گرفته است. انواع مختلف چهار ضلعی را میتوان به صورت کلی به شش دسته تقسیم کرد. این دستهها شامل مستطیل، مربع، لوزی، متوازی الاضلاع، ذورنقه و کایت هستند.
در ادامه به بررسی این شش دسته و خواص آنها پرداخته میشود.
مستطیل
نوع اول چهار ضلعیها مستطیل نامیده میشود که نمایی از آن در شکل زیر به تصویر کشیده شده است.
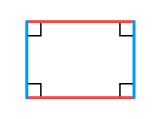
مستطیل، یکی از انواع چهار ضلعیها است که تمام زوایای آن برابر با 90 درجه و همچنین دو ضلع مقابل آن با یکدیگر هم اندازه باشند. نکته دیگری که باید به آن اشاره کرد این است که دو ضلع مقابل مستطیل موازی یکدیگر نیز هستند.
لوزی
دومین نوع از چهار ضلعیها، لوزی نامیده میشود که در شکل زیر به خوبی به تصویر کشیده شده است.
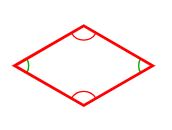
لوزی یک چهار ضلعی در نظر گرفته میشود که طول هر چهار ضلع آن با یکدیگر برابر و اضلاع رو به رو نیز موازی یکدیگر باشند. همچنین باید توجه کرد که در لوزی دو زاویه مقابل با یکدیگر برابر هستند. این موضوع را میتوان با توجه به اشکال زیر با جزئیات بیشتر متوجه شد.
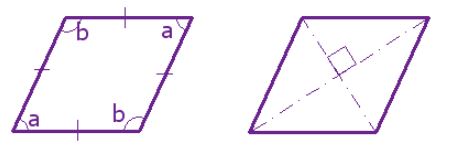
لوزیها عموما دو زاویه منفرجه یا باز و دو زاویه حاده یا بسته دارند. زاویه منفرجه زاویهای است که مقدار آن از 90 بیشتر باشد و زاویه حاده نیز زاویهای در نظر گرفته میشود که مقدار آن از 90 کمتر است. نکته جالبی که باید در مورد لوزی بیان کرد این است که قطرها در لوزی نیمساز زوایا نیز هستند.
برای آشنایی با محاسبه مساحت و محیط لوزی، پیشنهاد میکنیم به آموزشهای «مساحت لوزی — به زبان ساده (+ فیلم آموزش رایگان)» و «محیط لوزی — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.
مربع
نوع دیگری از چهار ضلعیها مربع است. یک مربع علاوه بر این که زوایای داخلی آن برابر با 90 درجه است، تمام اضلاع آن نیز با یکدیگر برابر هستند. شکل زیر یک مربع را به تصویر کشیده است.
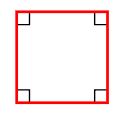
توجه کنید که دو ضلع مقابل مربع با یکدیگر موازی هستند. نکته دیگری که میتوان به آن اشاره کرد این است که مربع را میتوان یک زیر مجموعه از لوزیها (برابر بودن تمامی اضلاع) یا مستطیلها (تمام زوایای داخلی برابر با 90 درجه) نیز دانست.
متوازی الاضلاع
در ادامه چهارمین نوع از چهار ضلعیها که متوازی الاضلاع نامیده میشوند، مورد بررسی قرار میگیرد. شکل زیر یک متوازی الاضلاع را به تصویر کشیده است.
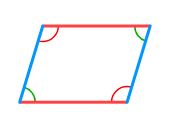
ویژگی مهم و مشخص متوازی الاضلاع این است که دو ضلع مقابل با یکدیگر هم اندازه و موازی باشند. این دو ویژگی سبب میشود که زوایای مقابل نیز با یکدیگر برابر باشند. همچنین خصوصیت دیگر متوازی الاضلاعها این است که مجموع دو زوایه مجاور یکدیگر برابر با 180 درجه است. این موضوع را میتوان با توجه به شکل زیر به خوبی متوجه شد.
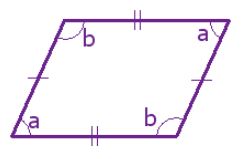
نکته مهمی که باید به آن توجه کنید این است که مربع، مستطیل و لوزی، یک نوع خاص و زیر مجموعهای از متوازی الاضلاعها محسوب میشوند. برای مثال یک متوازی الاضلاع که تمام اضلاع آن با یکدیگر برابر و زوایای آن نیز برابر با 90 درجه باشد را مربع مینامیم.
ذوزنقه
پنجمین نوع از چهار ضلعیها ذوزنقه نامیده میشود. ذوزنقه یک چهار ضلعی است که از دو ضلع یا وجه موازی با یکدیگر تشکیل شده است. شکل زیر نمونهای از این ذوزنقهها را به تصویر کشیده است.
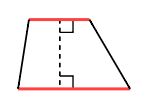
توجه کنید که اگر دو ضلع غیر موازی ذوزنقه (دو ساق ذوزنقه) با یکدیگر برابر باشند، ذوزنقه را ذوزنقه متساوی الساقین مینامند.
کایت
ششمین نوع از چهار ضلعیها را کایت یا شبه لوزی مینامند. طول اضلاع مجاور در یک کایت با یکدیکر برابر هستند و قطرها نیز به صورت عمود بر یکدیگر رسم میشوند. این موضوع در شکل زیر به خوبی نشان داده شده است.
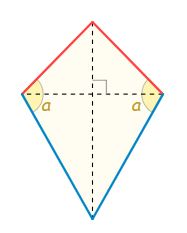
در یک کایت، قطرها بر یکدیگر عمود هستند و یک قطر، دیگری را نصف میکند. در واقع یک قطر عمود منصف قطر دیگر است.
دستهبندی چهار ضلعیها
در ادامه یک دستهبندی جامع از چهار ضلعیها به کمک یک نمودار درختی بیان میشود.
با استفاده از نمودار درختی شما میتوانید متوجه شوید که مربع یک مستطیل هست یا خیر که جواب آن بله است. همچنین شما میتوانید متوجه شوید که مستطیل یک کایت هست و یا خیر که جواب آن خیر است.
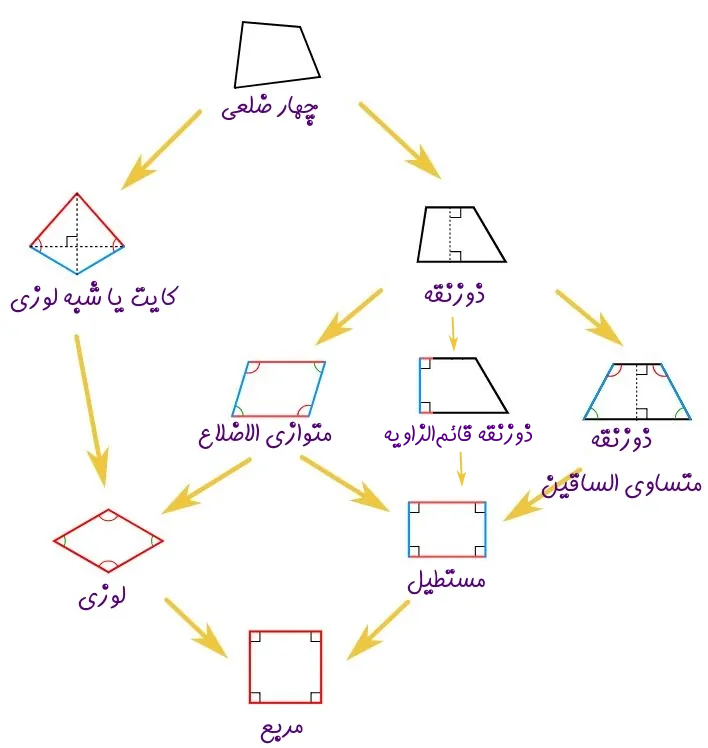
بنابراین همانطور که اشاره شد، با توجه به نمودار درختی بالا میتوان نشان داد که مربع، نوع خاصی از یک مستطیل و یک لوزی است. در واقع تمام مربعها را میتوان لوزی نیز نامگذاری کرد، ولی تمام لوزیها را نمیتوان مربع نامید. برای درک بهتر این موضوع به فلشهای نشان داده شده در شکل بالا و مفاهیم و تعاریف انواع چهار ضلعیها دقت کنید. با توجه و دقت به شکل بالا میتوان تمام پرسشها را در مورد چهار ضلعیها پاسخ داد.












چگونه قطر و خطوط موازی مستطیل و لوزی را بدونیم
با سلام و وقت بخیر؛
برای آشنایی با قطر و خطوط موازی مستطیل (طول و عرض آن)، مطالعه مطالب «قطر مستطیل چیست» و «طول و عرض مستطیل چیست؟» را به شما پیشنهاد میکنیم.
از همراهی شما با مجله فرادرس سپاسگزاریم.
نمودار شما یه نقص کوچولو داره ، بین ذوزنقه ی متساوی الساقین و متوازی الاضلاع ، یه شاخه ی دیگه ای از ذوزنقه با عنوان ذوزنقه ی قائم الزاویه باید رسم شه و از اون یه فلش به سمت مستطیل کشیده شه
سلام.
شکل بهروزرسانی شد.
سپاس از همراهی و بازخوردتان.
سلام در تعریف چند ضلعی در صفحه به هر خط شکسته بسته، چندضلعی گفته میشود به شرط اینکه ضلع ها یکدیگر را قطع نکنند ولی الان در تعریف شما اضلاع همدیگر را قطع کرده کدوم درست هست؟
سلام.
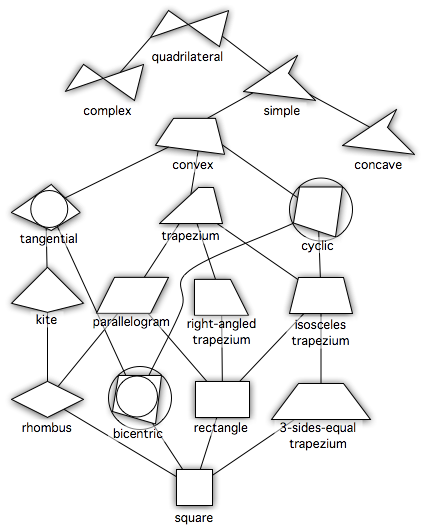
آنچه که چهارضلعی (ترجمه کلمه Quadrilateral) مینامیم، انواع مختلفی دارد. شکلی که به آن اشاره کردهاید، یکی از انواع چهارضلعی است که معمولاً در مدرسه به آن پرداخته نمیشود. آنچه در مدرسه بهعنوان «چهارضلعی» شناخته میشود، همان چیزی است که شما به آن اشاره کردید. در واقع، در مدرسه، چهارضلعی ساده (Simple) محدب (Convex) را بهعنوان چهارضلعی معرفی میکنند. شکل زیر انواع چهارضلعیها را نشان میدهد.
سالم و موفق باشید.
ممنونم خوب بود ولی لطفا تمام شکل های ذوزنقه را بگویید
سلام. متوازی الاضلاع یک ذوزنقه نیست لطفا اصلاح کنید
((تعریف ذوزنقه : چهار ضلعی که فقط دو ضلع موازی دارد.)) پس دو ضلع دیگه اگر موازی باشن(مثلا متوازی الاضلاع) دیگه ذوزنقه نداریم.
سلام.
در مورد تعریف ذوزنقه اختلاف نظر وجود دارد. برخی یک تعریف فراگیر و عدهای دیگر یک تعریف انحصاری برای ذوزنقه ارائه دادهاند. در واقع، عدهای معتقدند ذوزنقه دقیقاً دارای دو ضلع موازی است و برخی نیز میگویند ذوزنقه حداقل دو ضلع موازی دارد. براساس تعریف فراگیر، متوازیالاضلاع نوعی ذوزنقه است.
از همراهیتان با مجله فرادرس، خوشحالیم.
چرا جمع ضلع های مجاور ۱۸۰ میشود.
سلام.
همانطور که میدانیم، مجموع زوایای داخلی متوازیالاضلاع ۳۶۰ درجه است. از طرفی، طبق تعریف، زاویه رأسهای مقابل با هم برابر است. یعنی، اگر دو رأس مجاور A و B را داشته باشیم، رابطه ∠A+∠A+∠B+∠B=2∠A+2∠B=360∘ برقرار است و در نتیجه، ∠A+∠B=180∘ را خواهیم داشت که بیانگر این موضوع است که مجموع دو زاویه مجاور برابر با ۱۸۰ درجه است.
از اینکه با مجله فرادرس همراه هستید، خوشحالیم.