فرادرس
مساحت متوازی الاضلاع با قطر چگونه بدست می آید؟ + حل مثال
مساحت متوازی الاضلاع با قطر برابر «حاصلضرب قطرها در سینوس زاویه بین آن‌ها تقسیم بر دو» است. البته در صورت داشتن بردار معرف قطرهای متوازی‌الاضلاع نیز می‌توان مساحت آن محاسبه کرد. در این آموزش، فرمول‌ها و روش‌های محاسبه مساحت متوازی الاضلاع با قطر را به همراه حل چند مثال ارائه می‌کنیم.
مساحت متوازی الاضلاع چیست و چگونه محاسبه می‌شود؟
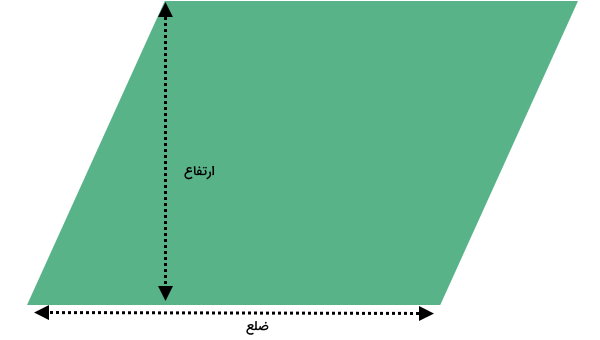
مساحت متوازی‌الاضلاع، اندازه سطحی است که این شکل هندسی پوشش می‌دهد. این اندازه، معمولا با ضرب قاعده در ارتفاع نظیر محاسبه می‌شود.
علاوه بر این، با داشتن اندازه قطرهای متوازی‌الاضلاع نیز می‌توانیم مساحت آن را به دست بیاوریم.
قطر متوازی الاضلاع چیست و چه کاربردی دارد؟
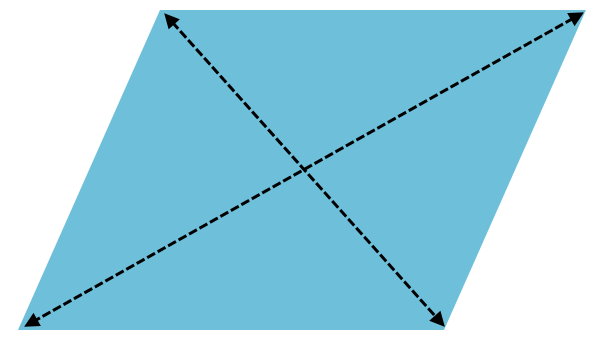
فاصله بین دو راس غیر مجاورِ چندضلعی‌ها، با عنوان قطر شناخته می‌شود. متوازی‌الاضلاع و دیگر چهارضلعی‌ها، دارای دو قطر هستند. در تصویر زیر، دو قطر یک متوازی‌الاضلاع را مشاهده می‌کنید. این قطرها، به منظور تعیین اندازه‌هایی مانند ضلع، محیط و مساحت مورد استفاده قرار می‌گیرند.
مساحت متوازی الاضلاع با قطر چگونه بدست می‌آید؟
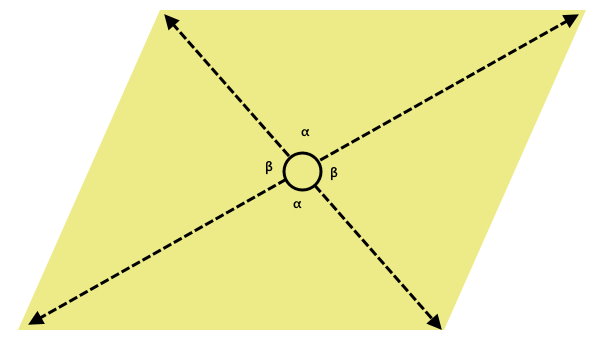
به منظور تعیین مساحت متوازی الاضلاع با قطر، علاوه بر اندازه قطرها، به اندازه یکی از زاویه‌های آن‌ها نیز نیاز داریم. این زاویه‌ها در تصویر زیر نمایش داده شده‌اند.
اگر اندازه قطرهای متوازی‌الاضلاع را برابر p و q در نظر بگیریم، مساحت متوازی الاضلاع با قطر از فرمول زیر به دست می‌آید:
$$
S = \frac {۱}{۲} pq \sin {\alpha}
$$
$$
S = \frac {۱}{۲} pq \sin {\beta}
$$
زوایای مجاور قطرهای متوازی‌الاضلاع، مکمل یکدیگر هستند. به همین دلیل، اندازه سینوس آن‌ها با یکدیگر برابر خواهد بود. از این‌رو، استفاده از هر یک از این زاویه‌ها، تغییری در نتیجه مساحت ایجاد نخواهد کرد.
مثال 1: تعیین مساحت متوازی‌الاضلاع با دو قطر
اندازه قطرهای یک متوازی‌الاضلاع به ترتیب برابر 12 و 5 سانتی‌متر است. اگر زاویه بین آن‌ها برابر 150 درجه باشد، مساحت متوازی‌الاضلاع چقدر است؟
فرمول مساحت متوازی‌الاضلاع با قطر به صورت زیر نوشته می‌شود:
$$
S = \frac {۱}{۲} pq \sin {\alpha}
$$
- S: مساحت متوازی‌الاضلاع
- p: یکی از قطرها برابر 12 سانتی‌متر
- q: قطر دیگر برابر 5 سانتی‌متر
- α: زاویه بین دو قطر برابر 150 درجه
سینوس زاویه 150 درجه برابر 0/5 است. این اندازه را به همراه دیگر اندازه‌های معلوم درون فرمول بالا قرار می‌دهیم:
$$
S = \frac {۱}{۲} \times ۱۲ \times ۵ \times \sin {۱۵۰^{\circ}}
$$
$$
S = ۶ \times ۵ \times ۰/۵
$$
$$
S = ۱۵
$$
در نتیجه، مساحت متوازی‌الاضلاع برابر ۱۵ سانتی‌متر مربع است.
مثال 2: محاسبه جبری مساحت متوازی‌الاضلاع با قطر
مساحت متوازی الاضلاع زیر را به دست بیاورید.
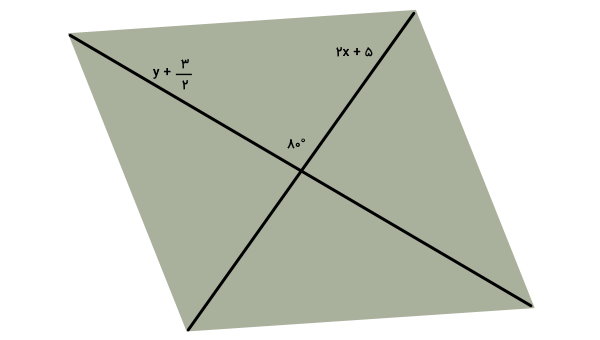
قطرهای متوازی‌الاضلاع بالا به صورت عبارت‌های جبری بیان شده‌اند. به همین دلیل، مساحت متوازی‌الاضلاع در این مثال، با استفاده قواعد از جمع و ضرب جبری محاسبه می‌شوند. برای این کار، باید عبارت‌های جبری معرف اندازه هر قطر را درون فرمول مساحت قرار دهیم:
$$
S = \frac {۱}{۲} pq \sin {\alpha}
$$
$$
S = \frac {۱}{۲} (y + \frac {۳}{۲}) (۲x+۵) \times \sin {۸۰^{\circ}}
$$
سینوس زاویه 80 درجه، حدودا برابر 0/98 است:
$$
S = \frac {۱}{۲} \times (۲xy + ۵y + ۳x + ۷/۵) \times ۰/۹۸
$$
$$
S = ۰/۴۹ \times (۲xy + ۵y + ۳x + ۷/۵)
$$
$$
S = ۰/۹۸xy + ۲/۴۵y + ۱/۴۷x + ۳/۶۷۵
$$
به این ترتیب، مساحت متوازی‌الاضلاع، بر حسب متغیرهای x و y به دست آمد. اگر مقادیر عددی x و y را داشته باشیم، امکان تعیین اندازه مساحت فراهم می‌شود.
مساحت متوازی الاضلاع با ضرب خارجی قطر
در بخش قبلی، فرمول مساحت متوازی الاضلاع با قطر را معرفی کردیم. اگر قطرهای متوازی‌الاضلاع، به صورت برداری بیان شوند، نحوه محاسبه مساحت متفاوت خواهد بود. در این شرایط، باید از ضرب خارجی بردارها استفاده کنیم.
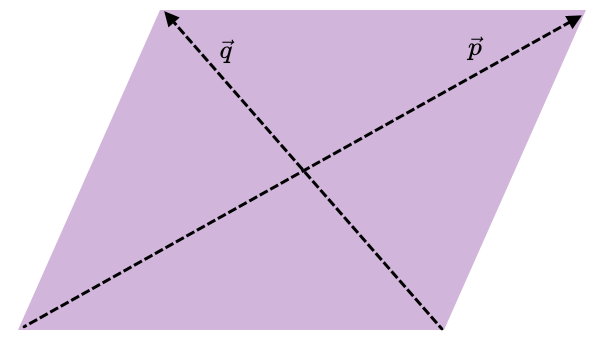
با ضرب خارجی بردارهای معرف قطر (بردارهای p و q)، مساحت متوازی‌الاضلاع به دست می‌آید:
$$
S = \frac {۱}{۲} \overrightarrow {p} \times \overrightarrow {q}
$$
مثال 3: محاسبه مساحت متوازی‌الاضلاع با بردار قطر
مساحت متوازی‌الاضلاعی با قطرهای زیر را حساب کنید.
$$
\overrightarrow {p} = (۱, ۲, ۳)
$$
$$
\overrightarrow {q} = (۴, ۵, ۶)
$$
بردارهای معرف قطرهای متوازی‌الاضلاع داده شده‌اند. محاسبه مساحت متوازی‌الاضلاع، با استفاده از فرمول زیر انجام می‌گیرد:
$$
S = \frac {۱}{۲} \overrightarrow {p} \times \overrightarrow {q}
$$
- S: مساحت متوازی‌الاضلاع
- p: بردار قطر اول (۱, ۲, ۳)
- q: بردار قطر دوم (۴, ۵, ۶)
برای شروع محاسبات، ابتدا نتیجه ضرب برداری بالا را توسط دترمینان تعیین کنیم:
$$
\overrightarrow {p} \times \overrightarrow {q} = \left|\begin{array}{ccc}
i & j & k \\
A_{۱} & A_{۲} & A_{۳} \\
B_{۱} & B_{۲} & B_{۳}
\end{array}\right|
$$
$$
=\left|\begin{array}{ccc}
i & j & k \\
۱ & ۲ & ۳ \\
۴ & ۵ & ۶
\end{array}\right|
$$
$$
= [i(۲ \times ۶ - ۳ \times ۵) -j(۱ \times ۶- ۳ \times ۴)+ k(۱ \times ۵ - ۲ \times ۴)]
$$
$$
= [i(۱۲ - ۱۵) -j(۶- ۱۲)+ k(۵ - ۸)]
$$
$$
= [i(-۳) -j(-۶)+ k(-۳)]
$$
$$
= -۳i+۶j-۳k
$$
$$
= (-۳, ۶, -۳)
$$
اندازه این ضرب بالا عبارت است از:
$$
|\overrightarrow {p} \times \overrightarrow {q}|=\sqrt{(-۳)^{۲}+۶^{۲}+(-۳)^{۲}}
$$
$$
=\sqrt{۹+۳۶+۹}
$$
$$
=\sqrt{۵۴}
$$
$$
=۷/۳۵
$$
حاصل ضرب خارجی را درون فرمول مساحت قرار می‌هیم:
$$
S = \frac {۱}{۲} \times ۷/۳۵
$$
$$
S = ۳/۶۷۵
$$
در نتیجه مساحت متوازی‌الاضلاع برابر 3/675 واحد سطح است.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت متوازی الاضلاع — هر آنچه باید بدانید» است. در ادامه، می‌توانید فهرست این مطالب را ببینید:
- متوازی الاضلاع چیست؟ — تعریف و مفاهیم به زبان ساده
- محیط متوازی الاضلاع چیست؟ — به زبان ساده + حل تمرین و مثال
- فرمول محیط متوازی الاضلاع چیست؟ — معرفی انواع فرمول ها + حل مثال
- مساحت متوازی الاضلاع چیست؟ — فیلم آموزش رایگان + حل تمرین و مثال
- محاسبه قطر متوازی الاضلاع — فرمول های محاسبه + حل تمرین و مثال
- محیط متوازی الاضلاع به صورت جبری — فرمول های ریاضی + حل مثال
- فرمول مساحت متوازی الاضلاع چیست؟ — تمامی فرمول ها + حل تمرین و مثال
- مساحت متوازی الاضلاع به صورت جبری — انواع فرمول ها + حل مثال
- نمونه سوال مساحت متوازی الاضلاع با جواب — حل تمرین های متنوع
- مساحت متوازی الاضلاع با قطر چگونه بدست می آید؟ + حل مثال(همین مطلب)
- مساحت متوازی الاضلاع با سینوس — به زبان ساده + حل مثال
