محور تقارن چند ضلعی منتظم چیست؟ — به زبان ساده

محور تقارن چند ضلعی منتظم خطی است که این شکل هندسی را به دو نیمه برابر تبدیل می‌کند. تمام چندضلعی‌های منتظم، به اندازه ضلع‌هایشان، محور تقارن دارند. در این مقاله، تعاریف و نحوه رسم محور تقارن چند ضلعی منتظم را مورد بررسی قرار می‌دهیم. علاوه بر این، مفاهیم مربوط به تقارن مرکزی و تقارن چرخشی چندضلعی‌های منتظم را نیز ارائه می‌کنیم.

محور تقارن چیست؟

محور تقارن یا خط تقارن، محور یا خطی فرضی است که شکل‌های هندسی را به دو قسمت مساوی و متقارن تقسیم می‌کند. اگر شکلی را حول یکی از محورهای تقارنش تا بزنیم، دو نیمه آن به طور کامل بر روی یکدیگر منطبق می‌شوند.

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

تصویر زیر، آزمایش تاخوردگی برای تشخیص محور تقارن یک مستطیل را نمایش می‌دهد.

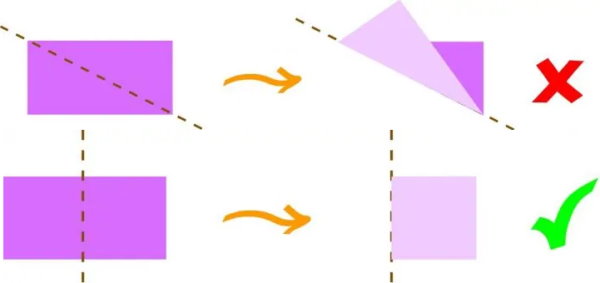
در حالت اول، با تا زدن مستطیل حول قطرش، دو نیمه آن بر روی هم منطبق نمی‌شوند. در نتیجه، قطر مستطیل، محور تقارن آن نیست. در حالت دوم، هر دو بخش، کاملا بر روی هم قرار می‌گیرند. بنابراین، راستای تاخوردگی در این حالت، یکی از محورهای تقارن مستطیل است. این نوع تقارن، با عنوان‌هایی نظیر تقارن محوری، تقارن انعکاسی و تقارن آینه‌ای شناخته می‌شود.

چند ضلعی منتظم چیست و چند محور تقارن دارد ؟

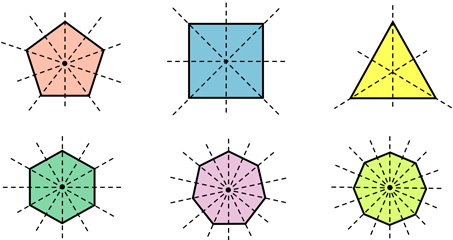
چندضلعی منتظم، یک چندضلعی با ضلع‌ها و زاویه‌های مساوی است. تمام چندضلعی‌های منتظم، دارای تقارن محوری و چند محور تقارن هستند.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

تعداد محورهای تقارن این چندضلعی‌ها، از روی تعداد ضلع‌های آن‌ها به دست می‌آید. به طور کلی، یک n ضلعی منتظم، دارای n محور تقارن است.

محور تقارن چند ضلعی منتظم چگونه رسم می شود ؟

رسم محور تقارن چند ضلعی منتظم، با توجه به فرد یا زوج بودن تعداد ضلع‌های آن انجام می‌گیرد.

رسم محور تقارن چند ضلعی منتظم با ضلع های فرد

اگر تعداد ضلع‌های چندضلعی منتظم، فرد باشد، برای رسم هر محور تقارن، کافی است یکی از راس‌ها را به مرکز ضلع مقابل آن راس وصل کنید. به عنوان مثال، مثلث متساوی الاضلاع (سه‌ضلعی منتظم) زیر را در نظر بگیرید.

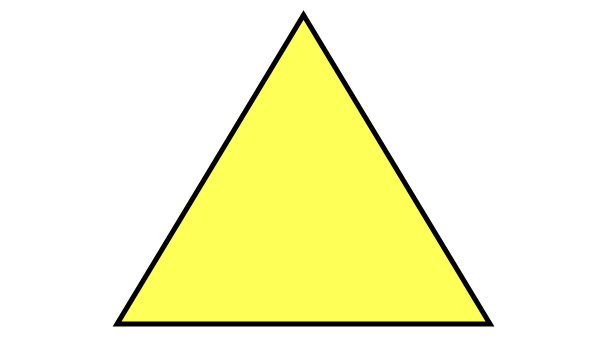
به منظور رسم محورهای تقارن سه‌ضلعی منتظم بالا، ابتدا مرکز هر ضلع را مشخص می‌کنیم.

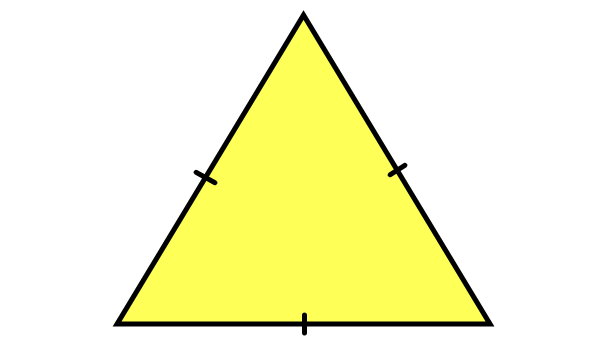
با اتصال هر راس به مرکز ضلع مقابل آن، یکی از محورهای تقارن ایجاد می‌شود.

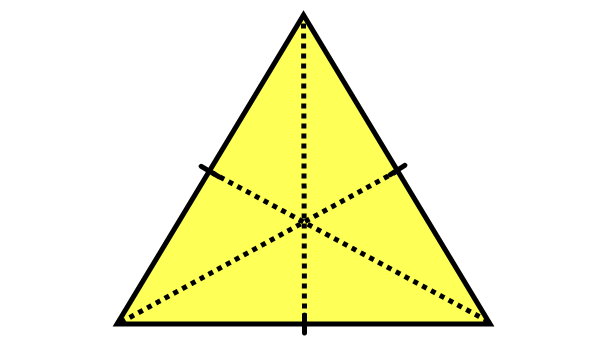
بر اساس محورهای رسم شده در تصویر بالا، مثلث متساوی الاضلاع، سه محور تقارن دارد. محورهای تقارن مثلث متساوی‌الاضلاع، همان ارتفاع مثلث هستند.

رسم محور تقارن چند ضلعی منتظم با ضلع های زوج

در صورت زوج بودن تعداد ضلع‌های چندضلعی منتظم، محورهای تقارن به دو گروه تقسیم می‌شوند. گروه اول، محورهای تقارنی هستند که رسم آن‌ها با اتصال راس‌های روبه‌رویی انجام می‌گیرد. گروه دوم، محورهای تقارنی هستند که رسم آن‌ها با اتصال مرکز ضلع‌های روبه‌رویی صورت می‌گیرد. به هر حال، تعداد محورهای تقارن در زوج ضلعی منتظم نیز مانند فرد ضلعی منتظم، برابر با تعداد ضلع‌ها است. به عنوان مثال، مربع (چهارضلعی منتظم) زیر را در نظر بگیرید.

به منظور رسم محورهای تقارن مربع بالا، هر گوشه را به گوشه مقابلش وصل می‌کنیم.

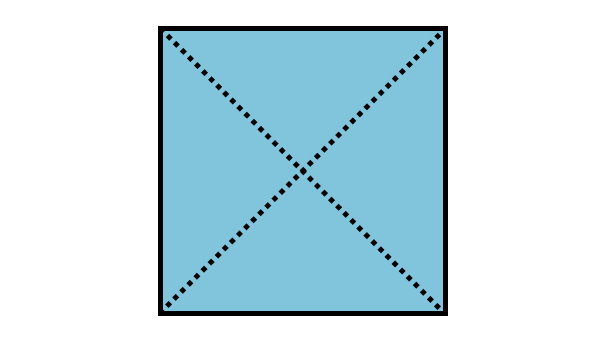
به این ترتیب، دو محور تقارن چهارضلعی منتظم بالا به دست می‌آید. این محورهای تقارن، همان قطرهای مربع هستند. می‌دانیم که یک n ضلعی منتظم، باید n محور تقارن داشته باشد. بنابراین، چهارضلعی منتظم، چهار محور تقارن دارد که دو مورد از آن‌ها را رسم کرده‌ایم. به منظور رسم دو محور تقارن بعدی، مرکز هر ضلع را علامت می‌زنیم.

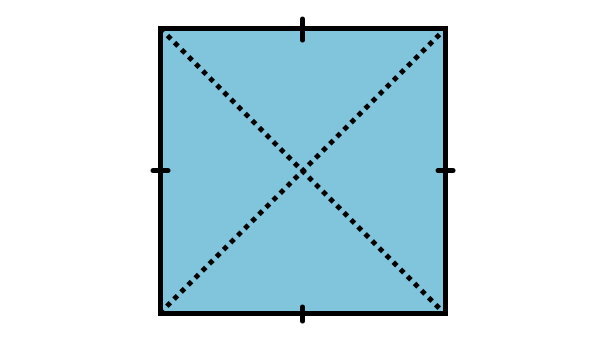
با اتصال مرکز ضلع‌های روبه‌رویی به هم، دو محور تقارن دیگر تشکیل می‌شوند.

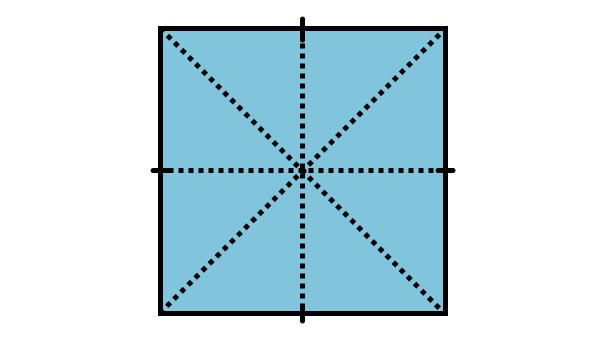
همان‌طور که مشاهده می‌کنید، مربع، چهار محور تقارن دارد. محورهای تقارن تمام چندضلعی‌های منتظم، با استفاده از یکی از دو روش معرفی شده در این بخش رسم می‌شوند.

سوال: یک چندضلعی منتظم، ۶ محور تقارن دارد. نام این چندضلعی چیست؟

جواب: تعداد محورهای تقارن چندضلعی‌های منتظم، برابر با تعداد ضلع‌های آن‌ها است. بنابراین، چندضلعی مورد سوال، یک شش‌ضلعی منتظم است.

مرکز تقارن چند ضلعی منتظم چیست ؟

در اشکال هندسی، اگر فاصله هر نقطه تا مرکز شکل با فاصله نقطه مقابل آن تا مرکز شکل برابر باشد، می‌گوئیم «شکل دارای تقارن مرکزی» است. در این حالت، نقطه مرکزی با عنوان «مرکز تقارن» شناخته می‌شود.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

برخی از چندضلعی‌های منتظم، دارای مرکز تقارن هستند. به عنوان مثال، فاصله هر نقطه از هشت‌ضلعی منتظم زیر تا مرکز شکل، با فاصله نقطه مقابل تا مرکز شکل یکسان است.

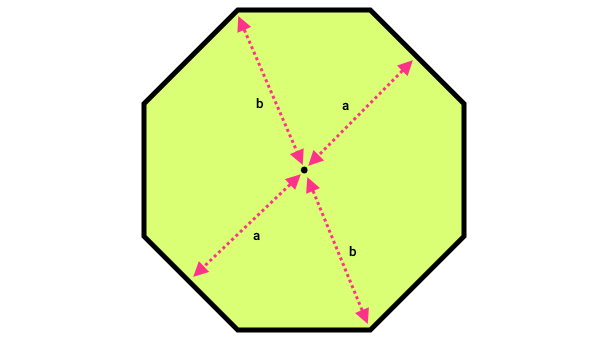
چندضلعی منتظم چند مرکز تقارن دارد؟

تقارن مرکزی چندضلعی منتظم، به تعداد ضلع‌های آن بستگی دارد. اگر تعداد ضلع‌های چندضلعی منتظم، فرد باشد، هیچ مرکز تقارنی در آن وجود نخواهد داشت. در صورت زوج بودن تعداد ضلع‌ها، چندضلعی منتظم، یک مرکز تقارن خواهد داشت.

تقارن دورانی یا تقارن چرخشی چند ضلعی منتظم چیست ؟

با چرخش یک چندضلعی منتظم، شکل آن نسبت به حالت اولیه تغییری نخواهد کرد. به این ویژگی، تقارن دورانی می‌گویند. تمام چندضلعی‌های منتظم، دارای تقارن دورانی هستند. البته، مرتبه تقارن دورانی چندضلعی‌های منتظم با یکدیگر تفاوت دارد.

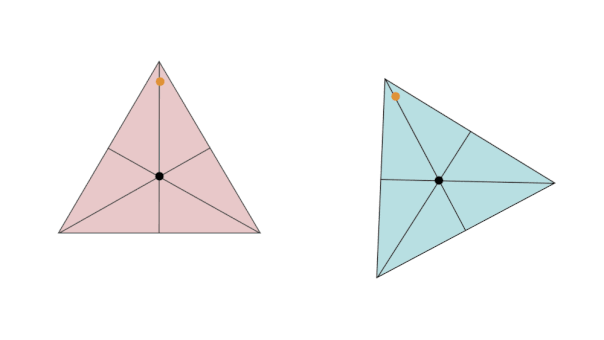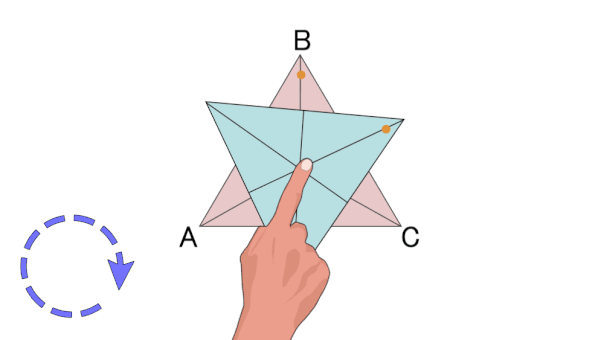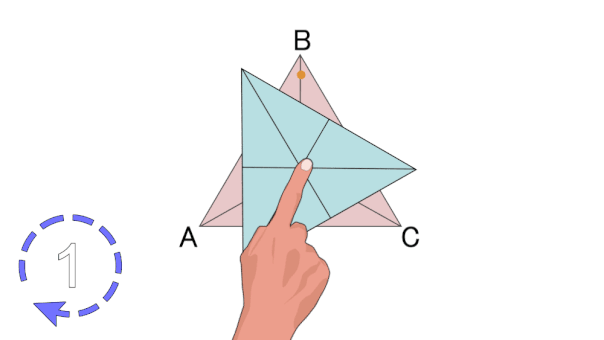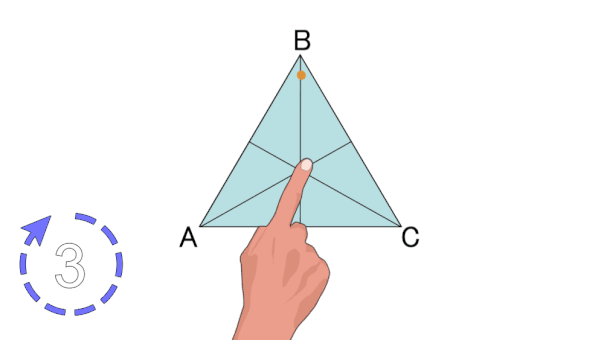
با چرخش مثلث متساوی الاضلاع حول مرکزش (تصویر بالا)، شکل مثلث، در سه زاویه به حالت اولیه بازمی‌گردد. بنابراین، این شکل، دارای تقارن دورانی مرتبه سه است. مرتبه تقارن دورانی چندضلعی منتظم، با تعداد ضلع‌های آن برابری می‌کند.

محاسبه زاویه تقارن چرخشی چند ضلعی منتظم

در هر n ضلعی منتظم، زاویه تقارن چرخشی از رابطه زیر محاسبه می‌شود:

$$
\frac { ۳۶۰ ^ { \circ } } { n }
$$

به عنوان مثال، زاویه تقارن چرخشی مربع، برابر است با:

$$
\frac { ۳۶۰ ^ { \circ } } { ۴ } = ۹۰ ^ { \circ }
$$

به عبارت دیگر، به اگر مربع را حول مرکزش، به اندازه ۹۰ درجه بچرخانیم، شکل آن به حالت اولیه خود بازمی‌گردد.

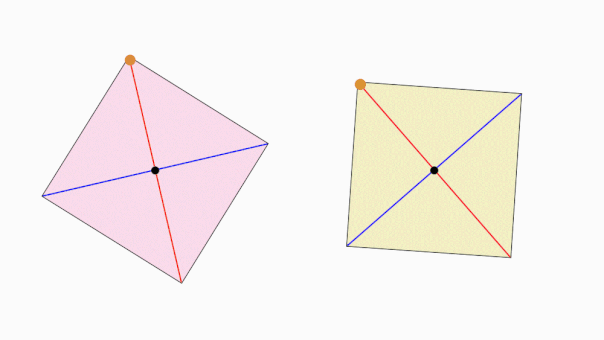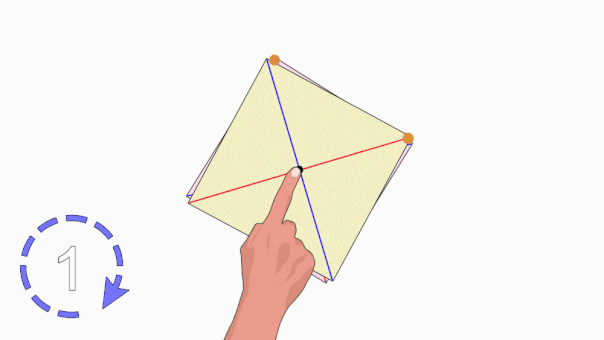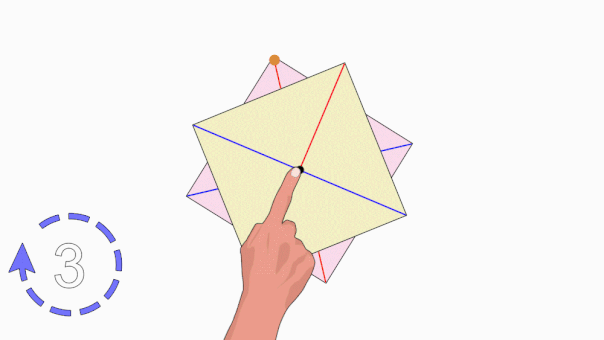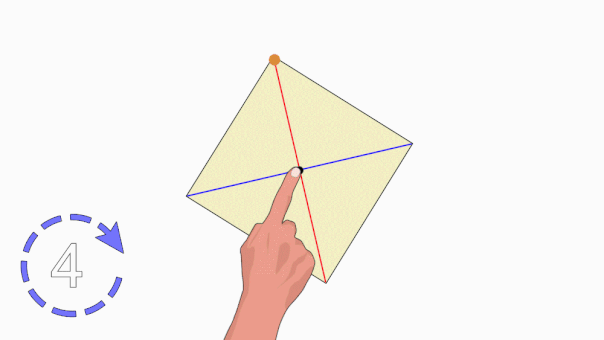
سوالات متداول در رابطه با محور تقارن چند ضلعی منتظم

در این بخش، به برخی از سوالات پرتکرار در رابطه با محور تقارن چند ضلعی منتظم به طور خلاصه پاسخ می‌دهیم.

آیا تمام چند ضلعی های منتظم محور تقارن دارند؟

بله.

هر n ضلعی منتظم چند محور تقارن دارد ؟

هر n ضلعی منتظم، n محور تقارن دارد.

فرمول محور تقارن چند ضلعی منتظم چیست؟

محور تقارن چندضلعی منتظم، برابر با n‌ است.

تعداد محور تقارن چند ضلعی منتظم چقدر است؟

تعداد محور تقارن چند ضلعی منتظم برابر با تعداد ضلع‌ها است.

هر n ضلعی منتظم چند مرکز تقارن دارد؟

هر n ضلعی منتظم، در صورت زوج بودن n، یک محور تقارن دارد و در صورت فرد بودن n، هیچ محور تقارنی ندارد.

پنج ضلعی منتظم چند محور تقارن دارد ؟

پنج ضلعی منتظم، ۵ محور تقارن دارد.

هفت ضلعی منتظم چند محور تقارن دارد ؟

هفت ضلعی منتظم، ۷ محور تقارن دارد.

هشت ضلعی منتظم چند محور تقارن دارد ؟

هشت ضلعی منتظم، ۸ محور تقارن دارد.

نه ضلعی منتظم چند محور تقارن دارد ؟

نه ضلعی منتظم، ۹ محور تقارن دارد.

ده ضلعی منتظم چند محور تقارن دارد ؟

ده ضلعی منتظم، ۱۰ محور تقارن دارد.

دوازده ضلعی منتظم چند محور تقارن دارد ؟

دوازده ضلعی منتظم، ۱۲ محور تقارن دارد.

شانزده ضلعی منتظم چند محور تقارن دارد ؟

شانزده ضلعی منتظم، ۱۶ محور تقارن دارد.

نام دیگر محور تقارن مثلث متساوی الاضلاع چیست؟

محورهای تقارن مثلث متساوی الاضلاع، ارتفاع و میانه این چندضلعی منتظم هستند.

نام دیگر محور تقارن زوج ضلعی منتظم چیست؟

محورهای تقارن زوج ضلعی‌های منتظم، قطرها و میانه ضلع‌های این شکل‌ها هستند.

نام دیگر محور تقارن فرد ضلعی منتظم چیست؟

محورهای تقارن فرد ضلعی‌های منتظم، میانه ضلع‌های این شکل هندسی هستند.