مساحت متوازی الاضلاع با سینوس — به زبان ساده + حل مثال

برای مساحت متوازی الاضلاع با سینوس، از زاویه بین دو ضلع مجاور یا زاویه بین دو قطر استفاده می‌شود. اگر اندازه دو ضلع مجاور یا اندازه دو قطر را داشته باشیم، می‌توانیم مساحت متوازی‌الاضلاع الاضلاع را به کمک فرمول «حاصلضرب ضلع‌های مجاور در سینوس زاویه بین آن‌‌ها» یا «یک‌دوم حاصل‌ضرب قطرها در سینوس زاویه بین آن‌ها» به دست بیاوریم. در این آموزش، فرمول‌ها و نکات مرتبط با محاسبه مساحت متوازی الاضلاع با سینوس را به همراه حل چند مثال ارائه می‌کنیم.

روش های محاسبه مساحت متوازی الاضلاع چه هستند؟

محاسبه مساحت متوازی‌الاضلاع، معمولا با ضرب قاعده در ارتفاع نظیر آن انجام می‌گیرد. البته، فرمول مورد استفاده برای تعیین مساحت متوازی‌الاضلاع، به اندازه‌های معلوم بستگی دارد.

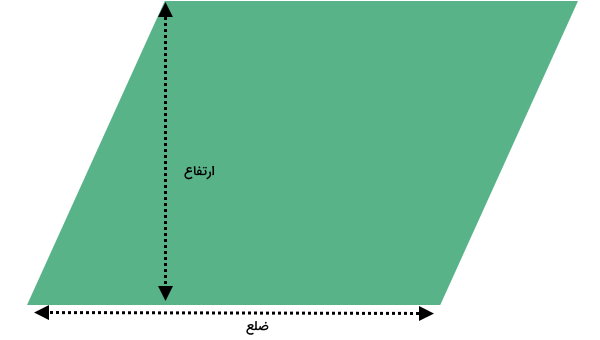
جدول زیر، برخی از فرمول‌های مساحت متوازی الاضلاع را با توجه به اندازه‌های معلوم نمایش می‌دهد.

فیلم آموزش ریاضی پایه هفتم

اینجا کلیک کنید

اگر اندازه‌ها یا بردارهای معرفی شده در جدول بالا را ندانیم یا امکان تعیین آن‌ها را نداشته باشیم، باید به سراغ روش‌های دیگری نظیر فرمول مساحت متوازی الاضلاع با سینوس برویم.

مساحت متوازی الاضلاع با سینوس چگونه بدست می‌آید؟

مساحت متوازی الاضلاع با سینوس، توسط اندازه دو ضلع و زاویه بین یا دو قطر و زاویه بین به دست می‌آید. به طور کلی، دو روش برای محاسبه مساحت متوازی الاضلاع با سینوس وجود دارد که در ادامه به معرفی آن‌ها می‌پردازیم.

مساحت متوازی الاضلاع با دو ضلع

در متوازی‌الاضلاع، ضلع‌های روبه‌رویی و زاویه‌های روبه‌رویی با هم برابر هستند. تصویر زیر، اندازه این ضلع‌ها زاویه‌ها را با حروف نمایش می‌دهد.

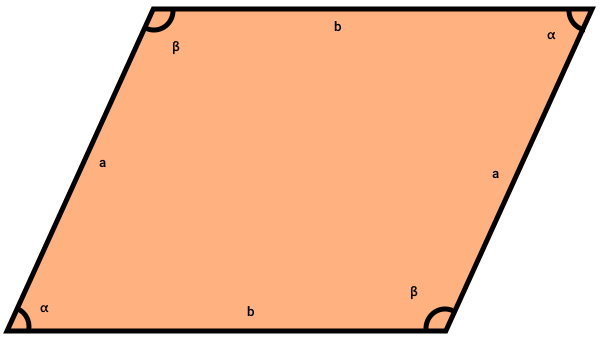
اگر زاویه بین دو ضلع متوازی‌الاضلاع را با α و β نمایش دهیم، فرمول محاسبه مساحت متوازی‌الاضلاع به صورت زیر نوشته می‌شود:

فیلم آموزش هندسه پایه دهم – هندسه ۱

اینجا کلیک کنید

$$
S = ab \sin {\alpha}
$$

در متوازی‌الاضلاع، زاویه راس‌های روبه‌رویی با هم برابر هستند. علاوه بر این، زاویه راس‌های مجاور، مکمل یکدیگرند. به دلیل برابر بودن سینوس زاویه‌های مکمل، استفاده از زاویه α یا β در نتیجه مساحت تاثیری نخواهد داشت. به عبارت دیگر، می‌توانیم به جای فرمول بالا از فرمول زیر نیز استفاده کنیم:

$$
S = ab \sin {\beta}
$$

مثال 1: محاسبه مساحت متوازی‌الاضلاع با سینوس و ضلع

اندازه ضلع‌های یک متوازی‌الاضلاع برابر 80 و 40 سانتی‌متر است. اگر زاویه یکی از راس‌ها برابر با 56 درجه باشد، مساحت متوازی‌الاضلاع چقدر خواهد بود؟

بر اساس فرمول مساحت متوازی‌الاضلاع با ضلع، داریم:

آموزش نگارش – پایه هفتم

شروع یادگیری

آموزش محاسبات سریع ریاضی

شروع یادگیری

آموزش عربی – پایه نهم

شروع یادگیری

آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی

شروع یادگیری

آموزش ریاضیات گسسته – پایه دوازدهم

شروع یادگیری

آموزش ریاضی پایه هفتم

شروع یادگیری

آموزش ریاضی و آمار ۱ – پایه دهم علوم انسانی

شروع یادگیری

آموزش هندسه پایه دهم – هندسه ۱

شروع یادگیری

آموزش ریاضی – پایه نهم

شروع یادگیری

آموزش ریاضی – پایه هشتم

شروع یادگیری

$$
S = ab \sin {\alpha}
$$

• S: مساحت متوازی‌الاضلاع
• a: اندازه یکی از ضلع‌ها برابر 80 سانتی‌متر
• b: اندازه ضلع دیگر برابر 40 سانتی‌متر
• α: یکی زاویه‌ها برابر 56 درجه

اندازه‌های معلوم را درون فرمول بالا قرار می‌دهیم:

$$
S = ۸۰ \times ۴۰ \times \sin {۵۶^{\circ}}
$$

سینوس زاویه 56 درجه حدود برابر 0/83 است:

$$
S = ۳۲۰۰ \times ۰/۸۳
$$

$$
S = ۲۶۵۶
$$

در نتیجه، مساحت متوازی‌الاضلاع برابر 2656 سانتی‌متر مربع است.

مثال ۲: محاسبه ارتفاع نظیر متوازی‌الاضلاع با سینوس

ضلع‌های مجاور متوازی‌الاضلاعی، 12 و 15 متر هستند. با فرض زاویه 36 درجه‌ای بین این دو ضلع، ارتفاع نظیر هر ضلع را حساب کنید.

در این مثال، اندازه دو ضلع و زاویه بین داده شده است. با استفاده از این اطلاعات می‌توانیم مساحت متوازی‌الاضلاع را به دست بیاوریم. با این وجود، صورت سوال، از ما اندازه ارتفاع‌های نظیر را می‌خواهد. می‌دانیم که یکی از روش‌های محاسبه مساحت متوازی‌الاضلاع، ضرب قاعده یا همان ضلع در ارتفاع نظیر است:

$$
S = b h
$$

از طرفی، مساحت متوازی‌الاضلاع با دو ضلع نیز از فرمول زیر به دست می‌آید:

$$
S = ab \sin {\alpha}
$$

اگر این دو فرمول را برابر با یکدیگر قرار دهیم، امکان تعیین ارتفاع با استفاده از اندازه ضلع‌ها فراهم می‌شود:

$$
bh= ab \sin {\alpha}
$$

• b: قاعده نظیر
• h: ارتفاع نظیر
• a: اندازه ضلع مجاور قاعده
• α: یکی از زاویه‌های متوازی‌الاضلاع

نکته مهم در این مسئله، این است که برای به دست آوردن ارتفاع‌های نظیر، باید محاسبات را دو بار انجام دهیم. در مرحله اول، ارتفاع نظیر ضلع 12 متری را تعیین می‌کنیم:

$$
bh= ab \sin {\alpha}
$$

• b: قاعده نظیر برابر 12 متر
• h: ارتفاع نظیر
• a: ضلع مجاور قاعده برابر 15 متر
• α: یکی از زاویه‌های متوازی‌الاضلاع برابر 36 درجه

سینوس زاویه 36 درجه، تقریبا برابر 0/59 است:

$$
۱۲ h= ۱۲ \times ۱۵ \times \sin {۳۶^{\circ}}
$$

$$
h= ۱۵ \times ۰/۵۹
$$

$$
h= ۸/۸۵
$$

ارتفاع نظیر ضلع 12 متری برابر ۸/۸۵ است. اکنون، ارتفاع نظیر ضلع 15 متری را محاسبه می‌کنیم:

$$
bh= ab \sin {\alpha}
$$

• b: قاعده نظیر برابر ۱۵ متر
• h: ارتفاع نظیر
• a: ضلع مجاور قاعده برابر ۱۲ متر
• α: یکی از زاویه‌های متوازی‌الاضلاع برابر 36 درجه

$$
۱۵ h= ۱۵ \times ۱۲ \times \sin {۳۶^{\circ}}
$$

$$
h= ۱۲ \times ۰/۵۹
$$

$$
h= ۷/۰۸
$$

در نتیجه، ارتفاع نظیر ضلع 15 متری برابر 7/08 است.

مساحت متوازی الاضلاع با دو قطر

در بخش‌های قبلی، فرمول محاسبه مساحت متوازی الاضلاع با بردارهای قطر را معرفی کردیم. آن فرمول، بر اساس ضرب خارجی بردارها نوشته شده بود.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی

اینجا کلیک کنید

از این‌رو، نیازی به دانستن زاویه بین قطرها وجود نداشت. متوازی الاضلاع زیر را در نظر بگیرید.

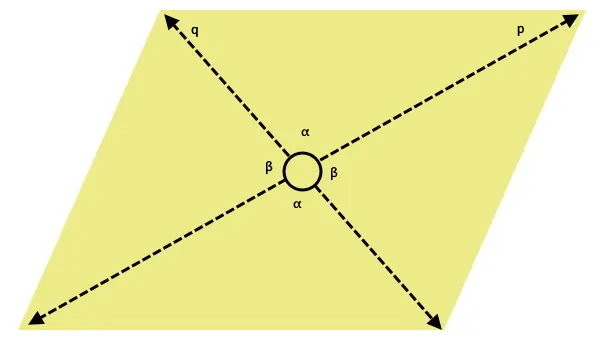
اندازه قطرهای متوازی‌الاضلاع با p و q و اندازه زاویه بین آن‌ها با α و β نمایش داده شده است. بر اساس این اندازه‌ها، فرمول مساحت متوازی‌الاضلاع با دو قطر و زاویه بین به صورت زیر نوشته می‌شود:

$$
S = \frac {۱}{۲} pq \sin {\alpha}
$$

زاویه‌های مقابل در محل برخورد قطرها، با هم برابر بوده و زاویه‌های مجاور، مکمل یکدیگرند. بنابراین، استفاده از هر یک از زاویه‌ها، تاثیری بر روی نتیجه نهایی نخواهد داشت. به عبارت دیگر، به جای فرمول بالا می‌توانیم از فرمول زیر نیز استفاده کنیم:

$$
S = \frac {۱}{۲} pq \sin {\beta}
$$

مثال ۳: محاسبه مساحت متوازی‌الاضلاع با سینوس و قطر

متوازی‌الاضلاعی به قطرهای 18 و 21 میلی‌متر را در نظر بگیرید. با فرض وجود زاویه 43 درجه‌ای بین قطرها، مساحت آن را به دست بیاورید.

فرمول مساحت متوازی‌الاضلاع با سینوس و قطر عبارت است از:

$$
S = \frac {۱}{۲} pq \sin {\alpha}
$$

• S: مساحت متوازی‌الاضلاع
• p: اندازه یکی از قطرها برابر 18 میلی‌متر
• q: اندازه قطر دیگر برابر 21 میلی‌متر
• α: زاویه بین قطرها برابر 43 درجه

$$
S = \frac {۱}{۲} \times ۱۸ \times ۲۱ \times \sin {۴۳^{\circ}}
$$

سینوس زاویه 43 درجه، حدودا برابر 0/68 است:

$$
S = \frac {۱}{۲} \times ۱۸ \times ۲۱ \times ۰/۶۸
$$

$$
S = ۱۲۸/۵۲
$$

در نتیجه، مساحت متوازی‌الاضلاع برابر 128/52 است.