مثلث متساوی الساقین چیست؟ | تعریف، ویژگی ها و محاسبات – به زبان ساده

در آموزش‌های پیشین مجله فرادرس با مثلث و روش‌های محاسبه محیط و مساحت آن آشنا شدیم. در این آموزش با نوع خاصی از مثلث‌ها به نام مثلث متساوی الساقین آشنا می‌شویم.

مثلث متساوی الساقین چیست ؟

در مطالب پیشین مجله فرادرس فهمیدیم مثلث چیست. همان‌طور که می‌دانیم، مثلث یک شکل هندسی است که سه ضلع و سه زاویه دارد و اهمیت آن از این جهت است که شکل‌هایی با اضلاع بیشتر را می‌توان به مثلث تجزیه کرد. بنابراین، شناخت مثلث و انواع آن مهم است.

مثلث متساوی الساقین، همان‌طور که از نام آن پیداست، مثلثی است که حداقل دو ضلع برابر دارد. شکل زیر یک مثلث متساوی الساقین را نشان می‌دهد که در آن، دو ضلع AB و AC برابر هستند و برابری آن‌ها با خط قرمز کوچکی روی خطوط مشخص شده است.

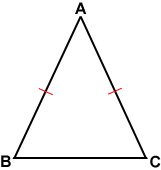
دو ضلع برابر مثلث متساوی الساقین، «ساق» (Leg) نامیده می‌شوند. ضلع سوم نیز «قاعده» (Base) نام دارد. زاویه مقابل به قاعده، «زاویه رأس» (Vertex Angle) نامیده می‌شود و زاویه‌های مقابل ساق‌ها «زاویه قاعده» هستند و با هم برابرند.

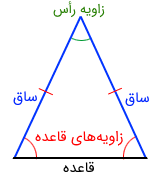
در یک مثلث متساوی الساقین معمولاً با طول سه بخش از آن کار داریم که در شکل زیر مشخص شده‌اند. ساق‌ها را با $$l$$، قاعده را با $$b$$ و ارتفاع را که از زاویه رأس بر قاعده عمود می‌شود، با $$h$$ نمایش می‌دهیم.

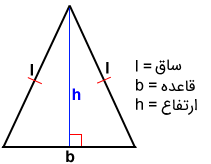
نکته ۱: ارتفاع، قاعده را نصف می‌کند و نیمساز زاویه رأس نیز هست.

نکته ۲: مثلث متساوی‌الساقین در حالت کلی یک خط یا محور تقارن دارد که ارتفاع آن است (اگر سه زاویه آن برابر باشند، سه خط تقارن دارد).

اگر دو مورد از سه طول بالا را داشته باشیم، سومی را می‌توان با استفاده از قضیه فیثاغورس به دست آورد.

• قاعده به شکل زیر به دست می‌آید:

$$\large h^2 + \left (\frac {b}{2} \right )^2 = l ^2 \Rightarrow \left (\frac {b}{2} \right )^2 = l ^2 – h ^2 \Rightarrow b = 2\sqrt {l^2-h^2}$$

• محاسبه ساق نیز به صورت زیر است:

$$\large h^2 + \left (\frac {b}{2} \right )^2 = l ^2 \Rightarrow l = \sqrt { h ^ 2 + \frac {b^2}{4} }$$

• ارتفاع با کمک قضیه فیثاغورس به شکل زیر محاسبه می‌شود:

$$\large \begin{array}{c} h ^ { 2 } + \left ( \frac { b } { 2 } \right ) ^ { 2 } = l ^ { 2 } \Rightarrow h ^ { 2 } + \frac { b ^ { 2 } } { 4 } = l ^ { 2 } \Rightarrow h^{2}=a^{2}-\frac{b^{2}}{4} \\ \Rightarrow h = \sqrt { l ^ { 2 } - \frac { b ^ { 2 } } { 4 } } \end {array}$$

بنابراین، برای به دست آوردن طولِ قاعده، ساق و ارتفاع، از فرمول‌های زیر کمک می‌گیریم:

$$\large \boxed { \begin{array} { l } b = 2 \sqrt { l ^ { 2 } - h ^ { 2 } } \\ l = \sqrt { h ^ { 2 } + \frac { b ^ { 2 } } { 4 } } \\ h = \sqrt { l ^{ 2 } - \frac { b ^ { 2 } } { 4 } } \end {array} }$$

محیط مثلث متساوی الساقین

برای به دست آوردن محیط مثلث متساوی الساقین، کافی است اندازه سه ضلع آن را با هم جمع کنیم.

مساحت مثلث متساوی الساقین

اگر اندازه قاعده $$b$$ و ارتفاع $$h$$ مثلث متساوی الساقین را داشته باشیم، مساحت آن به سادگی با فرمول نصف حاصل‌ضرب قاعده در ارتفاع به دست می‌آید:

فیلم آموزش محاسبه مساحت مثلث – رایگان در فرادرس

کلیک کنید

$$\large \boxed {A = \frac 12 b h }$$

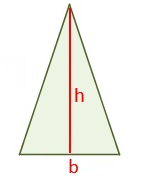
برای آشنایی بیشتر با روش‌های محاسبه مساحت مثلث متساوی الساقین به آموزش «مساحت مثلث متساوی الساقین | محاسبه به زبان ساده» در این لینک مراجعه کنید.

انواع مثلث متساوی الساقین

مثلث متساوی الساقین با توجه به اندازه زاویه رأسش می‌تواند انواع مختلفی داشته باشد. اگر زاویه رأس مثلث متساوی الساقین کوچک‌تر از ۹۰ درجه (حاده) باشد، مثلث متساوی الساقین حاده نام دارد. اگر اندازه زاویه رأس برابر با ۹۰ درجه یا قائمه باشد، مثلث متساوی الساقین قائم‌الزاویه داریم. مثلث متساوی‌الساقینی که زاویه رأس آن بزرگ‌تر از ۹۰ درجه باشد، منفرجه نام دارد. و در نهایت، مثلث متساوی‌الساقینی را که سه زاویه برابر داشته باشد، مثلث متساوی الساقین متساوی الزوایا یا متساوی الاضلاع می‌نامیم.

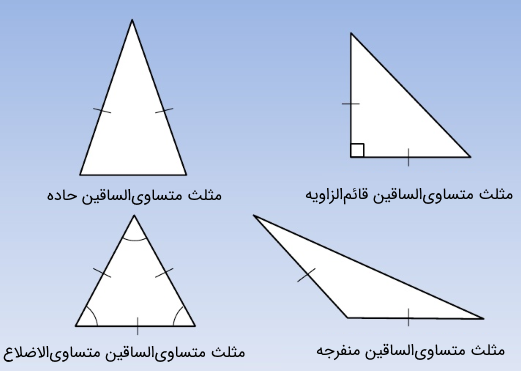
مثال های مثلث متساوی الساقین

در این بخش، چند مثال را از مثلث متساوی الساقین بررسی می‌کنیم.

مثال اول مثلث متساوی الساقین

کدام‌یک از مثلث‌های زیر متساوی الساقین است؟

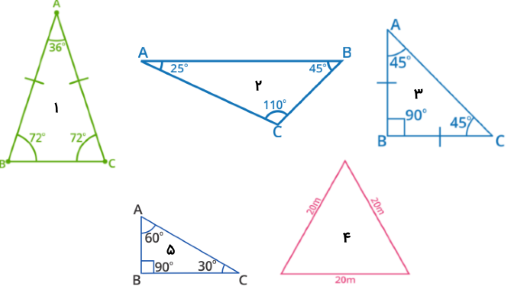
حل: با توجه به اینکه مثلث‌های ۱، ۳ و ۴ حداقل دو ضلع برابر دارند، متساوی الساقین هستند.

مثال دوم مثلث متساوی الساقین

در مثلث شکل زیر د زاویه A و B برابرند. مقدار $$x$$ را به دست آورید.

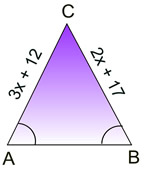
حل: با توجه به اینکه دو زاویه برابر هستند، مثلث متساوی الساقین بوده و در نتیجه، دو ساق AC و BC با هم برابرند. بنابراین، داریم:

$$\large AC = BC \Rightarrow 3 x + 12 = 2 x + 17 \\ \large 3x-2x=17-12 \Rightarrow x = 5$$

مثال سوم مثلث متساوی الساقین

مساحت مثلث متساوی الساقین زیر را محاسبه کنید.

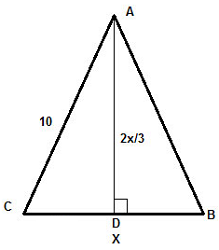
حل: مساحت مثلث برابر است با:

$$\large A = \frac 12 b h =\frac 12\times x \times \frac {2x}{3}=\frac {x^2}{3}$$

با توجه به اینکه ارتفاع مثلث متساوی الساقین قاعده را نصف می‌کند، دو مثلث قائم الزوایه داریم که برابرند و می‌توانیم از قضیه فیثاغورس برای به دست آوردن اندازه قاعده ($$x$$) استفاده کنیم:

$$\large 10 ^ 2 = \left( \frac x 2 \right) ^2 + \left( \frac {2x} { 3} \right) ^2 \Rightarrow 10 ^2 = \frac {x^2}{4}+\frac{4x^2}{9} \\ \large 100=\frac {28x^2+16x^2}{28} \Rightarrow x^2 =\frac {700}{11}$$

مساحت مثلث نیز برابر است با:

$$\large A =\frac {x^2}{3}= \frac {700}{ 3 \times 11} \approx 21.21$$