دایره چیست؟ — تعریف و مفاهیم به زبان ساده + فیلم آموزش رایگان

اشکال مختلف هندسی در زندگی ما کاربردهای زیادی دارند و در طول تاریخ الهامبخش فعالیتهای انسان بودهاند. دایره نیز یکی از ابتداییترین این اشکال هندسی است. نخستین کاربرد دایره، چرخ بوده که از دیرباز به کار رفته است. یکی دیگر از نمودهای دایره در زندگی بشر، حلقه ازدواج است. دایره در فرهنگها، مراسم سنتی و آیینی، شهرسازی، اندیشههای هنری و به ویژه در ابزارآلات نجومی جایگاهی نمادین و کاربردی دارد. در فرهنگ و عرفانهای شرقی از قدیم دایره نماد آسمان، جهان پاک، افلاک گردنده و ماهیتهای غیردنیوی بوده است. در این آموزش به این پرسش پاسخ میدهیم که دایره چیست و چه ویژگیهایی دارد.
فیلم آموزشی دایره و محاسبات آن
دایره چیست ؟
«دایره» (Circle) مجموعه همه نقاطی از یک صفحه است که در فاصله یکسانی از یک نقطه مرکزی قرار دارند.
دایره فقط از نقاط مرزی تشکیل شده است. فاصله بین نقطه میانی و مرز دایره را «شعاع» مینامند. پارهخطی که نقاط انتهایی آن روی دایره باشد و از نقطه میانی عبور کند «قطر» نامیده میشود. قطر دو برابر شعاع است. همچنین، پارهخطی که نقاط انتهایی آن روی مرز دایره قرار دارند، اما از مرکز عبور نمیکند، «وتر» نامیده میشود.
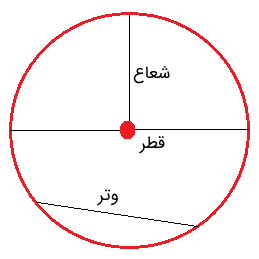
شعاع، قطر و محیط دایره چیست ؟
شعاع، قطر و محیط دایره مهمترین ویژگیهای دایره هستند که با هریک از آنها میتوان دایره را تعریف کرد.
همچنین، اگر یکی از این پارامترها را داشته باشیم، دو مورد دیگر نیز به دست خواهند آمد.
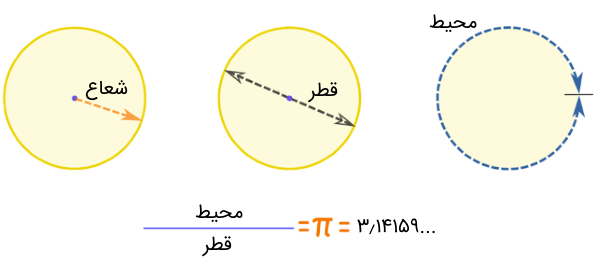
تعریف این پارامترها به شرح زیر است:
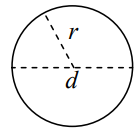
- شعاع دایره (Radius): فاصله مرکز دایره تا محیط که معمولاً آن را با نشان میدهند. هر دایره بینهایت شعاع دارد.
- قطر (Diameter): خط مستقیمی که از محیط دایره شروع میشود، از مرکز دایره عبور میکند و به نقطه مقابل خودش در محیط دایره میرسد. قطر را معمولاً با حرف مشخص میکنند. دایره بینهایت قطر دارد.
- محیط دایره (Circumference): فاصله نقطه آغاز و پایان ترسیم دایره را محیط دایره مینامند. به عبارت دیگر، فاصلهای که در آن، نقطه شروع کشیدن دایره به خودش برمیگردد محیط دایره است.
قطر، وتر، کمان و مماس دایره چیست ؟
از آنجا که علم هندسه و دایرهها از زمانهای دور مورد مطالعه قرار میگرفتهاند، اصطلاحات و عبارات مختلفی در این علم به وجود آمدهاند تا مطالعه و پژوهش در این زمینه را سادهتر کنند.
از طرفی، تا زمانی که عبارتی مانند «قطر» وجود داشته باشد، هیچ کس ترجیح نخواهد داد به جای آن بگوید: «خط مستقیمی که از محیط دایره شروع میشود، از مرکز دایره عبور میکند و به نقطه مقابل خودش در محیط دایره میرسد.» در ادامه، تعدادی از رایجترین اصطلاحات در مورد دایرهها را معرفی خواهیم کرد.
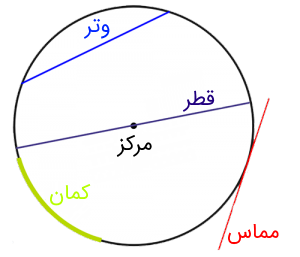
- وتر (Chord): خطی که از یک نقطه بر روی محیط دایره به نقطه دیگری از آن میرسد.
- قطر (Diameter): اگر وتر از مرکز دایره عبور کند، به آن «قطر» میگوییم قطر بزرگترین وتر در دایره است. هر دایره، بینهایت قطر دارد.
- مماس (Tangent): خطی که دایره را در یک نقطه لمس میکند.
- کمان یا قوس (Arc): قسمتی از محیط دایره.
قطعه و قطاع دایره چیست ؟
دایرهها دو قطعه (قطاع) اصلی دارند:
- قطاع (Sector): قطاع چیزی شبیه به تکههای پیتزا است که با دو شعاع دایره محصور شده است.
- قطعه (Segment): قطعه بخشی از دایره است بین یک کمان و یک وتر از دایره محصور شده است.
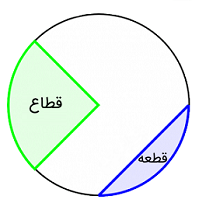
رایجترین قطعات دایره، ربعدایره و نیمدایره هستند. «ربع» (Quadrant) یکچهارم از سطح دایره است و «نیمدایره» (Semicircle) نیمی از سطح دایره است.
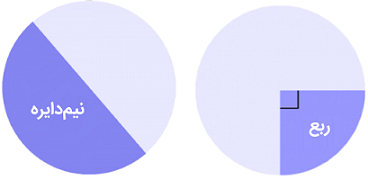
از قطاعهای متداول دایره میتوان به نیمدایره و ربع دایره اشاره کرد. برای آشنایی با نحوه محاسبه محیط و مساحت این قطاعها، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
- محیط نیم دایره چیست؟ — به زبان ساده + حل تمرین و مثال
- مساحت نیم دایره چگونه بدست میآید؟ — به زبان ساده + حل مثال
- محیط ربع دایره چیست؟ — به زبان ساده + حل تمرین و مثال
- مساحت ربع دایره چیست؟ — به زبان ساده + حل تمرین و مثال
درون، بیرون و مرز دایره چیست ؟
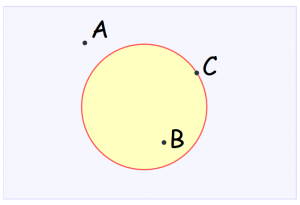
دایرهها مانند تمام اشکال دیگر، «درون» و «بیرون» و «مرز» دارند. وقتی چیزی دقیقاً بین درون و بیرون دایره قرار گرفته باشد، میگوییم آن چیز روی دایره قرار دارد.
در شکل زیر، نقطه A بیرون دایره، نقطه B درون دایره و نقطه C روی دایره قرار دارند.
فرمول محیط دایره چیست ؟
با توجه به قطر یا شعاع دایره، میتوانیم فرمول محیط دایره را بیان کنیم.
فرمول محیط دایره با قطر
محیط دایرهای به قطر با فرمول زیر به دست میآید:
فرمول محیط دایره با شعاع
محیط دایرهای به شعاع برابر است با:
برای آشنایی بیشتر با روش محاسبه محیط دایره، به آموزش «محیط دایره — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.
فرمول مساحت دایره چیست ؟
با توجه به قطر یا شعاع دایره، میتوانیم فرمول مساحت دایره را بیان کنیم.
فرمول مساحت دایره با شعاع
مساحت دایره به شعاع برابر است با:
فرمول مساحت دایره با قطر
مساحت دایرهای به قطر به صورت زیر است:
برای آشنایی بیشتر با محاسبه مساحت دایره و مثالهای آن، پیشنهاد میکنیم به آموزش «مساحت دایره — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید. محیط و مساحت دایره را میتوان به کمک سایتهای اینترنتی نیز به دست آورد. اگر علاقه به یادگیری نحوه کار با این سایتها دارید، مطالعه زیر را به شما پیشنهاد میکنیم:
- محاسبه محیط دایره آنلاین — بهترین سایتها + حل تمرین
- محاسبهگر مساحت دایره آنلاین — بهترین سایتها + حل تمرین و مثال
معادله دایره چیست ؟
دایره زیر را در دستگاه مختصات دکارتی در نظر بگیرید.
مرکز این دایره نقطه و شعاع آن برابر با است.
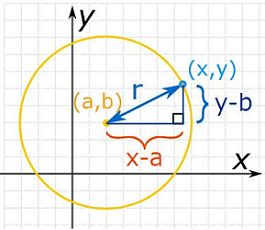
با کمک قضیه فیثاغورس، معادله این دایره به صورت زیر خواهد بود:
برای آشنایی بیشتر با معادله دایره، به آموزش «معادله دایره — به زبان ساده (+ دانلود فیلم آموزش رایگان)» مراجعه کنید.
فرمول محاسبه وتر دایره چیست ؟
همانطور که گفتیم، وتر پارهخطی در یک دایره است که هر دو نقطه از محیط دایره را به هم متصل میکند. همان دو نقطه توسط محیط به شکل قوس یا کمان دایره به هم متصل میشوند.
دایره شکل زیر را در نظر بگیرید. در دایره داده شده با مرکز M، پارهخط AB نشان دهنده قطر دایره، یعنی بلندترین وتر است و OE شعاع دایره خواهد بود. همچنین، پارهخط BX نشان دهنده وتر دایره است، در حالی که منحنی BX کمان خواهد بود.
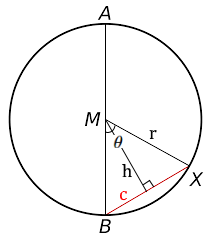
میتوانیم طول وتر را از طول شعاع و زاویه ایجاد شده توسط خطوط متصل مرکز دایره به دو انتهای وتر BX تعیین کنیم.
همچنین اگر شعاع و طول نیمساز زاویه را بدانیم، میتوانیم طول وتر را نیز محاسبه کنیم. عمود از مرکز M به وتر BX کشیده میشود وتر BX را نصف میکند. بنابراین با استفاده از قضیه فیثاغورس میتوانیم به راحتی طول وتر BX را پیدا کنیم.
فرض کنید طول شعاع دایره ، اندازه خط عمود از مرکز بر وتر و طول وتر باشد. همچنین، را به عنوان زاویه بین دو شعاع MB و MX در نظر بگیرید.
دو فرمول اساسی برای یافتن طول وتر دایره به شرح زیر است:
- طول وتر با استفاده از فاصله عمود از مرکز دایره بر وتر برابر است با:
- طول وتر با استفاده از اندازه شعاع و زاویه بین دو شعاعی که از دو نقطه دو سر وتر میگذرند، به صورت زیر است:
قضیه کمان و وتر دایره چیست ؟
طبق قضیه کمان و وتر، اگر در دایره شکل زیر، طول وترهای و برابر باشند، یعنی ، آنگاه طول کمانهای و برابر است، یعنی .
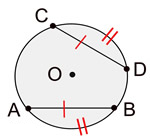
اثبات: پارهخطهای ، ، و را رسم میکنیم.
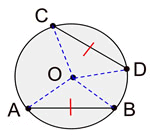
با توجه به اینکه این پارهخطها شعاع هستند، اندازه همه آنها برابر است:
با توجه به تساوی بالا، دو مثلث همنهشت هستند. بنابراین، زاویههای و نیز برابرند. از این موضوع نیز میتوان نتیجه گرفت که کمتنهای مقابل آنها با هم برابر است و قضیه اثبات میشود:
عکس قضیه کمان و وتر دایره: اگر در دایره شکل بالا، طول کمانهای و برابر باشند، یعنی ، آنگاه طول وترهای و برابر است، یعنی .
اثبات عکس قضیه کمان و وتر مشابه اثباتی است که در بالا بیان کردیم.
دایره و عدد پی
از تقسیم محیط دایره بر قطر آن، به عدد ...۳٫141592654 میرسیم که در ریاضیات به آن عدد «پی» (Pi) گفته میشود. عدد پی را در زبان ریاضی با علامت «π» نشان میدهیم. عدد پی، نسبت محیط دایره به قطر آن است. بنابراین، اگر قطر دایره برابر با عدد یک باشد، محیط آن برابر با ...۳٫141592654 خواهد بود. نسبت محیط دایره به شعاع آن نیز برابر 2π است. این نسبت در فرمول محیط دایره با شعاع مورد استفاده قرار میگیرد.
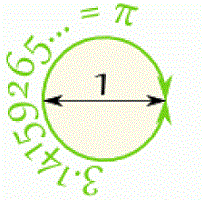
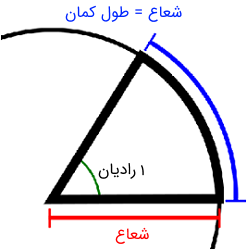
عدد در مثلثات بسیار مهم است، زیرا تفسیر طبیعیتری از زاویهها ارائه میدهد (نسبت به درجهها). به طور خاص، رادیان به گونهای تعریف شده است که رادیان معادل یک دایره کامل است. بدین صورت، زاویه با طول کمان متناظر است که در آن، شعاع دایره است. به طور معادل، رادیان به گونهای تعریف میشود که یک رادیان متناظر با طول کمان برابر با شعاع دایره است.
چگونه یک دایره را رسم کنیم؟
برای رسم دایره، ابتدا نقطهای را به عنوان نقطه مرکزی یا همان مرکز دایره مشخص میکنیم. سپس با یک فاصله ثابت (شعاع)، دور آن یک منحنی بسته رسم میکنیم. در این حالت خواهیم دید که مرکز توسط منحنی احاطه شده و فاصله آن با تمام نقاط روی منحنی یکسان است.
ابزار لازم برای رسم دایره به شرح زیر است:
- یک صفحه کاغذ
- یک عدد پونز یا سوزن تهگرد
- یک قطعه نخ نسبتاً محکم
- یک عدد مداد
یک سر نخ را به پایه پونز (سنجاق) و طرف دیگر آن را به مداد ببندید. پونز را طوری در کاغذ مقوا فرو کنید که محکم باشد. اکنون مداد را تا جایی که نخ، کشیده، محکم و صاف بایستد، از پونز دور کنید؛ یک نقطه روی کاغذ بگذارید و با چرخاندن مداد، کشیدن منحنی را ادامه دهید تا دایره کامل شود.

معرفی فیلم آموزش هندسه پایه دهم (هندسه ۱) فرادرس
برای آشنایی بیشتر با چندضلعیها و محاسبه مساحت و محیط آنها، پیشنهاد میکنیم به فیلم آموزش هندسه پایه دهم (هندسه ۱) مراجعه کنید که توسط فرادرس تهیه شده است. این آموزش ویدیویی که مدت زمان آن ۴ ساعت و ۳ دقیقه است، در چهار درس تهیه شده است.
در درس اول این آموزش، موضوعات ترسیمهای هندسی و استدلال بیان شدهاند. مباحث درس دوم، به قضیه تالس و تشابه مثلثها و کاربردهای آنها اختصاص یافته است. در درس سوم، مباحث مربوط به چندضلعیها و ویژگیهایی از آنها و همچنین، مساحت و کاربردهای آن مورد بیان شده است. در نهایت، موضوع درس چهارم، تجسم فضایی است که خط، نقطه و صفحه و همچنین تفکر تجسمی را شامل میشود.
- برای مشاهده فیلم آموزش هندسه پایه دهم (هندسه ۱) + اینجا کلیک کنید.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش های بدست آوردن محیط و مساحت دایره + حل تمرین و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- دایره چیست ؟ — تعریف و مفاهیم به زبان ساده + فیلم آموزش رایگان(همین مطلب)
- شعاع چیست ؟ — شعاع دایره به زبان ساده (+ فیلم آموزش رایگان)
- وتر چیست ؟ — به زبان ساده
- عدد پی (Π) چیست ؟ — کاربردها به زبان ساده
- قطاع و مقطع دایره و محاسبات آن در هندسه — به زبان ساده
- محیط دایره به زبان ساده + حل تمرین و فیلم آموزش رایگان
- مساحت دایره به زبان ساده + حل تمرین
- فرمول محیط دایره چیست ؟ + حل تمرین و مثال
- فرمول مساحت دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- نسبت محیط دایره به قطر آن چیست ؟ — به زبان ساده
- نسبت محیط دایره به شعاع آن چیست ؟ — به زبان ساده
- مساحت نیم دایره چگونه بدست می آید ؟ — به زبان ساده + حل مثال
- مساحت ربع دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محاسبه محیط دایره آنلاین — بهترین سایت ها + حل تمرین
- محیط نیم دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط ربع دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محاسبه گر مساحت دایره آنلاین — بهترین سایت ها + حل تمرین و مثال
- محیط و مساحت دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط دایره با چی متناسب است ؟ — به زبان ساده + حل تمرین و مثال
- فرمول محیط و مساحت دایره چیست ؟ — به زبان ساده + حل مثال
- دایره چند شعاع دارد ؟ — تصویری و به زبان ساده
- مماس دایره چیست و چه ویژگی هایی دارد؟ — به زبان ساده + حل تمرین و مثال
- کمان دایره چیست ؟ — محاسبه طول و اندازه + حل مثال
- قطر دایره چیست ؟ — رسم و محاسبه قطر + حل تمرین و مثال
- قطعه دایره چیست ؟ — فرمول محیط و مساحت + حل مثال
- قطاع دایره چیست ؟ — فرمول های محاسبه محیط و مساحت + حل مثال و تمرین













سلام وقت بخیر من میخوام محاسبه پله گرد را یاد بگیرم میشه کمکم کنین…
عالی خیلی مطالب مفیدی گذاشتید تو سایتتون 😍🙏
سلام تعداد وتر هایی که طولشون بین وتر ماکزیمم و مینیمم هست چند تاست ؟
سلام.ببخشید میخواستم ببینم میتونم از بخشی از این مطالب در یک تحقیق دانش آموزی استفاده کنم؟قراره در یک جایی قرار بگیره که خیلیا ببینن البته منبعش آدرس این سایت رو هم ذکر میکنم.با تشکر
سلام، وقت شما بخیر؛
در صورتیکه تحقیق شما به صورت آفلاین منتشر میشود و روی اینترنت قرار نمیگیرد استفاده از محتوای مجله فرادرس در آن با ذکر منبع مانعی ندارد.
شرایط استفاده از مجله فرادرس را میتوانید به صورت دقیق در این لینک مطالعه کنید.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.
سلام من یه قطعه ازدایره رودارم به اندازه طول۱۱۲ونیم وارتفاع۱۲ونیم چجوری تواتوکد قطر کامل اون دایره روبه دست بیارم چندمیشه قطرش؟؟؟من فقط یه تیکه از دایره رودارم به اون اندازه ای ک گفتم قطرش چندمیشه
سلام ،روزتان بخیر ببخشید ولی آیا دایره طول هم دارد
سلام.
اگه بخواهیم قیمت п ره ادامه بدیم بعد اعشار باید کدوم اعداد تقسیم بشه
قطر/محیط=3.1415
محیط=؟
قطر؟
سلام.
طول یک کمیت برای اندازهگیری فاصله بین دو نقطه است. بنابراین، «طول دایره» مفهوم خاصی ندارد. اما مواردی مانند طول شعاع دایره، طول قطر دایره، طول وتر دایره و… معنی دارند. شاید منظورتان اندازه محیط دایره باشد. در کل، باید مشخص کنید که منظورتان از طول دایره چیست.
از همراهیتان با مجله فرادرس، خوشحالیم.
با سلام و خسته نباشید . داخل متن این دو تا رو اشتباه نوشتید فک کنم
شعاع (Diameter)
قطر (Radius)
باید
اینطوری می شد قطر (Diameter) و شعاع (Radius)
فرض کنید نخی داریم به طولی معین ( عددی گویا که قابل اندازه گیری است مثلآ 50 سانتی متر) که دو سر آن به هم متصل است.
با چه روش عملی ای میتوان چنین نخی با مدار بسته را به شکل یک دایرهٔ دقیق در آورد.
این به این معنی است که بدون داشتن اندازه شعاع (چون شعاع چنین دایرهای حتمأ باید یک عدد گنگ باشد)، قادر به ترسیم دایره ای با معلوم بودن محیط آن( که عددی گویا است) باشیم.
سلام.
اصلاحات لازم انجام شد.
از همراهی و بازخورد شما سپاسگزاریم.
درود بر شما مهندس
مطالب عالی و آموزنده بود.
موفق باشید.
انتگرال بگیر. بازه انتگرال هم جاهایی که دو دایره باهم تقاطع دارن بزار
بیشتر از همه اینکه با تصویر یاد داده بودید خیلی در فهم سریع مطالب کمک میکنه من که فقط تصاویر رو دیدم و لذت بردم
سلام بنده میخواهم یک نیم دایره کوچک را از یک نیم دایره بزرگتر کم کنم با چه فرمولی انجام دهم
واقعا عالی بوددست شمادرد نکنه
عالی عالی عالی……
با سپاس از توضیحات ساده و خوبتان. فقط یک سوال ذهن من را درگیر کرد. با این توضیحاتی که دادید، فرق دقیق بین مساحت و محیط در چیست؟ آیا مساحت همان محیط نمی باشد؟
نه اینگونه نیست
محیط دور تا دور شکل است ولی مساحت یعنی داخل شکل
باسلام و خدا قوت
آسان ، روان ، دقیق ، همه فهم
سلام ممنون از اطلاعات بسیار مفیدتون
ممنونم مفید بود?
سلام خیلی متشکرم
مثال اگروتر100باشدوقوس25
100تقسیم بر2که میشود50
50ضربدر50میشود2500
25ضربدر25میشود625
وحالا2500به اضافه625میکنیم میشود3125وحالاتقسیم بردوبرابرقوس که میشود125شعاع دایره میشود125
ازلطف وزحمات شما متشکرم.اللرین آغریماسین
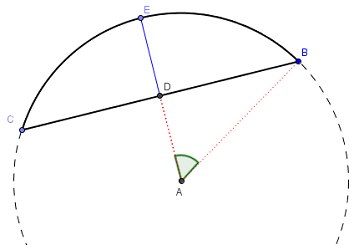
سلام ما اندازه وتر را داریم و ارتفاع وطر تا قوس هم مشخص است شعاع دایره چجوری به دست میاد
سوال منم همینه??
سلام. شکل زیر را در نظر بگیرید. در این شکل، h=DE ارتفاع و a=DB نصف طول وتر است. برای مثلث ADB روابط a=rsinθ و r−h=rcosθ را داریم که در آنها، r شعاع دایره و θ زاویه مشخص شده در نقطه A است. اکنون دو عبارت را به توان دو رسانده و با هم جمع میکنیم: a2+(r−h)2=(rsinθ)2+(rcosθ)2=r2. در نهایت، شعاع دایره با فرمول r=2ha2+h2 به دست میآید.
واقعا مفید و عالی .سپاسگذارم?
تشکر خیلی خوب بود