حجم چیست؟ | تعریف، فرمول های حجم و نحوه محاسبه — به زبان ساده و با مثال

در این آموزش از مجموعه مطالب ریاضی مجله فرادرس، میخواهیم به این پرسش پاسخ دهیم که حجم چیست و چگونه میتوان حجم اشکال هندسی مختلف را محاسبه کرد. همچنین، با واحدهای استاندارد و رایج حجم آشنا میشویم و مثالهایی را از نحوه محاسبه حجم بیان خواهیم کرد.
حجم چیست؟
«حجم» (Volume) اندازهگیری گنجایش یا ظرفیتی است که یک جسم میتواند در خود نگه دارد. به عنوان مثال، اگر یک فنجان بتواند 100 میلیلیتر آب را تا حد لبه خود نگه دارد، گفته می شود که حجم آن 100 میلیلیتر است. حجم را میتوان به عنوان مقدار فضای اشغال شده توسط یک جسم سهبعدی یا شکل جامد نیز تعریف کرد.
حجم جامد مانند مکعب یا مکعب مستطیل با شمارش تعداد واحد مکعب موجود در آن اندازهگیری میشود. بهترین راه برای تجسم حجم، فکر کردن بر اساس فضای محصور/اشغالشده توسط هر جسم سهبعدی یا شکل جامد است. این موضوع را میتوان با یک تمرین ساده در خانه مشاهده کرد:
- یک برگه مستطیل شکل به طول مثلاً ۲۰ سانتیمتر و عرض ۱۰ سانتیمتر بردارید.
- بدون اینکه ورق را تا بزنید، اضلاع مقابل برگه را به هم بچسبانید.
- اکنون یک جسم سهبعدی ساختهاید که فضای داخل آن را یک صفحه دوبعدی محصور کرده است.
آشنایی با حجم های هندسی
در این بخش، چند حجم هندسی مهم و رایج را معرفی میکنیم.
مکعب مستطیل چیست؟
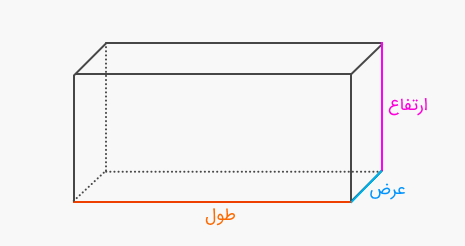
«مکعب مستطیل» یک شکل هندسی سهبعدی است که شش رویه یا وجه مستطیل شکل دارد. همه زوایای مکعب مستطیل قائمه هستند. مکعب مربع یا همان مکعب، حالت خاصی از مکعب مستطیل است. شکل زیر یک مکعب مستطیل را همراه با طول، عرض و ارتفاع آن نشان میدهد.
مخروط چیست؟
مخروط یک حجم هندسی است که از یک قاعده دایرهای صاف شروع شده و به آرامی به یک نقطه میرسد که یک محور را به مرکز قاعده میسازد. این نقطه رأس نام دارد. همچنین، میتوانیم مخروط را به عنوان هرمی تعریف کنیم که دارای یک سطح مقطع دایرهای است. این مخروطها به عنوان مخروط دایرهای نیز شناخته میشوند.
طبق یک تعریف دقیقتر، مخروط شکلی است که با مجموعهای از پارهخطهایی تشکیل میشود که یک نقطه مشترک به نام رأس را به تمام نقاط مرز یک قاعده دایرهای متصل میکنند. فاصله از رأس و طول مخروط از رأس تا هر نقطه از محیط قاعده «یال» نامیده میشود.
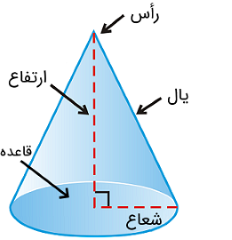
شکل زیر رأس، ارتفاع، یال، قاعده و شعاع قاعده مخروط را نشان میدهد.
منشور چیست؟
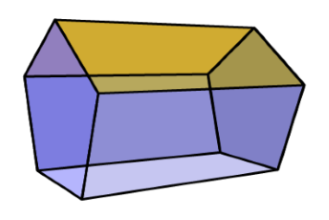
منشور حجمی است هندسی که دو وجه از وجههای آن مشابه هستند و به آنها «قاعده» میگوییم. قاعدههای منشور میتوانند مثلث، مربع، مستطیل یا هر چندضلعی دیگری باشند. سایر وجههای منشور مستطیل یا متوازیالاضلاع هستند. دقت کنید که قاعدههای منشور انحنا ندارند و باید چندضلعی باشند. شکل زیر یک منشور را نشان میدهد که قاعده آن پنجضلعی است.
کره چیست؟
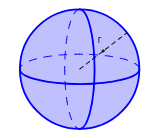
«کره» (Sphere) یک جسم هندسی کاملاً گرد در فضای سهبعدی است. این حجم هندسی را میتوان با مجموعهای از تمام نقاط واقع در فاصله برابر (شعاع) از یک نقطه (مرکز) مشخص کرد. کره کاملاً متقارن است و لبه و رأس ندارد. شکل زیر یک کره با شعاع r را نشان میدهد.
استوانه چیست؟
«استوانه» یک حجم است که دو دایره موازی و هماندازه در بالا و پایین دارد. این دایرهها را «قاعده» مینامیم. فاصله بین دو قاعده را نیز «ارتفاع» میگوییم. اگر قاعدههای بالا و پایین استوانه در یک راستا باشند، استوانه را قائم و اگر بر هم منطبق نباشند، استوانه را مایل مینامیم. شکل زیر استوانه مایل و قائم را نشان میدهد.

فرمول حجم اشکال هندسی
هر جسمی در محیط اطراف ما ماهیت اشغال فضا را دارد. این اجسامِ زندگی واقعی را میتوان به راحتی با اشکال سهبعدی در هندسه مقایسه کرد. مهمترین اشکال هندسی سهبعدی که ممکن است با آنها سر و کار داشته باشیم مکعب، مکعب مستطیل، استوانه، هرم، مخروط و کره هستند. در ادامه، با جزئیات بیشتری به حجم هریک از این شکلها نگاهی میاندازیم.
حجم مکعب مستطیل
مکعب مستطیل شکل زیر را در نظر بگیرید.
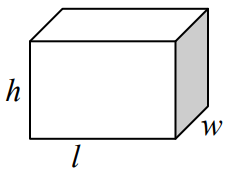
حجم این مکعب مستطیلی به ارتفاع ، طول و عرض به صورت زیر است:
حجم مکعب
مکعب زیر داده شده است.
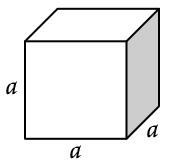
حجم این مکعب به اضلاع ، برابر خواهد بود با:
حجم استوانه
استوانه زیر را در نظر بگیرید.
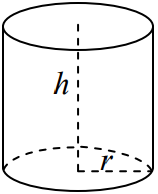
حجم این استوانه با ارتفاع و شعاع قاعده برابر است با:
برای آشنایی بیشتر با روش محاسبه و مثالهای حجم استوانه به مطلب «حجم استوانه و محاسبه آن — به زبان ساده» در این لینک مراجعه کنید.
حجم هرم
هرم زیر را در نظر بگیرید.

حجم این هرم با ارتفاع و اضلاع قاعده و با فرمول زیر محاسبه میشود:
حجم مخروط
مخروط زیر را در نظر بگیرید.
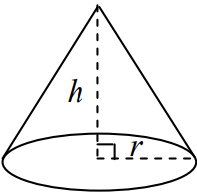
حجم مخروطی به شعاع قاعده و ارتفاع ، برابر است با:
برای آشنایی بیشتر با محاسبه حجم مخروط و مثالهای آن، پیشنهاد میکنیم به آموزش «حجم مخروط و محاسبه آن | به زبان ساده» در این لینک مراجعه کنید.
حجم مخروط ناقص
یک مخروط ناقص در شکل زیر نشان داده شده است.

برای محاسبه حجم یک مخروط ناقص با ارتفاع ، شعاع قاعده بالای و شعاع قاعده پایین از فرمول زیر استفاده میکنیم:
حجم منشور
منشور زیر داده شده است.
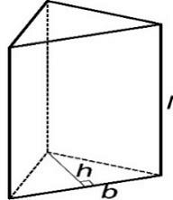
حجم منشوری به طول و قاعده قاعده و ارتفاع قاعده برابر است با:
حجم کره
کره زیر داده شده است.
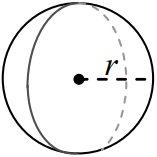
حجم کرهای با شعاع به صورت زیر محاسبه میشود:
برای آشنایی بیشتر با محاسبه حجم کره و مثالهای آن، پیشنهاد میکنیم به آموزش «حجم کره و محاسبه آن | به زبان ساده» در این لینک مراجعه کنید.
واحد حجم
دیدیم که حجم کمیت یا مقداری از فضای سه بعدی است که توسط یک مایع، جامد یا گاز اشغال شده است. در برخی موارد، حجم را ظرفیت یا «گنجایش» (Capacity) نیز مینامند. حتماً از رسانهها شنیدهاید که مثلاً گنجایش یک سد ۵٫۹ میلیارد متر مکعب است یا در زندگی روزمره خود دیدهاید که برای مثال، حجم یک پاکت شیر که از فروشگاه میخرید، ۲۵۰ سیسی است. این دو موردِ متر مکعب و سیسی و موارد مشابهی که حتماً مشاهده کردهاید، واحدهای مختلف حجم هستند.
همانطور که اشاره کردیم، حجم بخشی از فضای سهبعدی است توسط یک جسم را اشغال شده است. به عنوان نمونه، حجم مکعب مستطیل شکل زیر با ضلعهای 4 و 5 و 10 به شکل زیر به دست میآید:
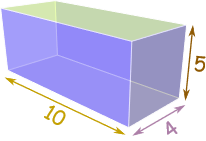
[۳واحد] ۲۰۰ = [واحد] ۱0 × [واحد] ۴ × [واحد] ۵
همانطور که میدانیم، واحد طول در دستگاه بینالمللی یکاها یا SI، متر (m) است و با توجه به «۳واحد» برای حجم، یکای آن در SI، «متر مکعب» (Cubic Meter) است. یک متر مکعب (m3)، برابر با حجم مکعبی به اضلاع ۱ متر است.
سانتیمتر مکعب (cm3) نیز واحد معروف دیگری برای حجم است. سانتیمتر مکعب یا سیسی (cc) واحدی برای حجم مکعبی به ضلع یک سانتیمتر است. سیسی به صورت ccm نیز نمایش داده میشود.
شاید بتوان گفت رایجترین واحدهای اندازهگیری حجم که در زندگی روزمره با آنها سر و کار داریم، «لیتر» و «میلیلیتر» هستند. هر لیتر برابر است با یکهزارم متر مکعب. به عبارت دیگر، یک لیتر حجمی برابر با 10cm×10cm×10cm را اشغال میکند.
برای تبدیل واحدهای رایج و استاندارد حجم، میتوانید از جدول زیر استفاده کنید.
| لیتر | متر مکعب | واحد اندازهگیری |
| = 1000 | = ۱ | ۱ متر مکعب |
| = 158٫987294928 | = 0٫158987294928 | ۱ بشکه |
| = 28٫316864592 | = 0٫028316846592 | ۱ فوت مکعب |
| = 1 | = 0٫001 | ۱ دسیمتر مکعب |
| = 1 | = 0٫001 | ۱ لیتر |
| = 3٫785411784 | = 0٫003785411784 | ۱ گالن (آمریکایی) |
| = 0٫473176473 | = 0٫000473176473 | ۱ پاینت (آمریکایی) |
| = 0٫016387064 | = 0٫000016387064 | ۱ اینچ مکعب |
| = 0٫001 | = 0٫000001 | ۱ سانتیمتر مکعب (سیسی) |
مثال های محاسبه و تبدیل واحد حجم
در این بخش، چند مثال را از محاسبه حجم و تبدیل واحد آن بررسی میکنیم.
مثال اول حجم
استوانه زیر را در نظر بگیرید که ارتفاع و شعاع قاعده آن داده شده است. حجم این استوانه را محاسبه کنید.
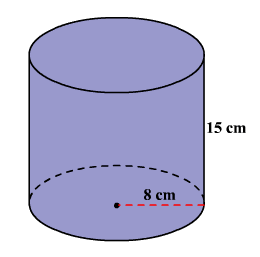
حل: همانگونه که در شکل نیز میبینیم، ارتفاع و شعاع قاعده استوانه داده شدهاند. بنابراین به راحتی حجم استوانه به دست میآید:
مثال دوم حجم
مخروط ناقص شکل زیر داده شده است. اندازه ارتفاع و شعاع دو قاعده این مخروط ، و هستند.
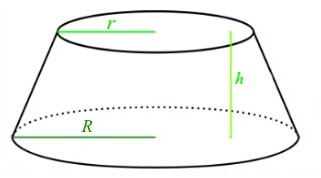
حجم این مخروط ناقص را محاسبه کنید.
حل: در اینجا از فرمول محاسبه حجم مخروط ناقص استفاده میکنیم و به آسانی حجم را محاسبه میکنیم:
مثال سوم حجم
کره شکل زیر با قطر داده شده است. حجم این کره را محاسبه کنید (مقدار را برابر با در نظر بگیرید).
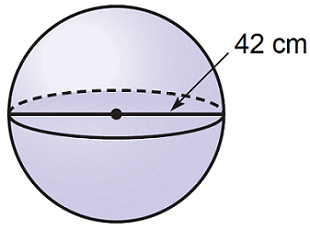
حل: همان طور که گفته شد، قطر کره برابر با است. بنابراین، شعاع آن خواهد بود. اکنون به راحتی میتوانیم حجم کره را محاسبه کنیم:
مثال چهارم حجم
احتمالاً مشاهده کردهاید که افراد در هنگام بیان مشخصات یخچالها عددی را بیان میکنند که برحسب فوت است. مثلاً میگویند فلان یخچال ۱۸ فوت است. منظور از این عدد همان ظرفیت یا حجم یخچال است و واحد صحیح آن فوت مکعب است که به اشتباه فوت گفته میشود. اکنون میخواهیم ببینیم ۱۸ فوت مکعب معادل چند لیتر است؟
حل: با استفاده از جدول تبدیل واحد بالا، میتوان نوشت:
۱۸ ft3 = ۱۸ × 28٫3 = ۴۹۱ L
مثال پنجم حجم
۹ لیتر، چند سیسی است؟
حل: با توجه به جدول تبدیل واحد بالا، یک سیسی برابر با 0٫001 لیتر است. در نتیجه، هر لیتر برابر با ۱۰۰۰ سیسی است و بنابراین، ۹ لیتر برابر خواهد بود با:
۹۰۰۰ سیسی = ۱۰۰۰ × ۹ = ۹ لیتر













در بخش واحد حجم، یک غلط املایی وجود دارد:
خو => خود
سلام و روز شما بهخیر؛
از دقت نظر شما ممنونیم. اشتباه متن تصحیح شد.
با تشکر از همراهی شما دوست عزیز با مجله فرادرس.
خیلی عالی استاد محترم تشکر