محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال

محیط مثلث متساوی الساقین برابر جمع اندازه دو ساق با قاعده آن است. به طور کلی، محاسبه محیط مثلث با جمع اندازه سه ضلع انجام می‌شود. البته در مثلث‌های خاص نظیر مثلث متساوی الاضلاع، مثلث متساوی الساقین و مثلث قائم الزاویه، فرمول‌ها و روش‌های دیگر برای تعیین محیط وجود دارند. در این مطلب، نحوه محاسبه محیط مثلث متساوی الساقین را به زبان ساده و به همراه حل چندین مثال متنوع آموزش می‌دهیم.

مثلث متساوی الساقین چیست ؟

مثلث متساوی الساقین، شکلی با 3 ضلع و 3 گوشه است که دو ضلع آن با هم برابرند. به ضلع‌های برابر این مثلث، «ساق» گفته و به ضلع سوم آن، «قاعده» می‌گویند. تصویر زیر، شکل یک مثلث متساوی الساقین را نشان می‌دهد.

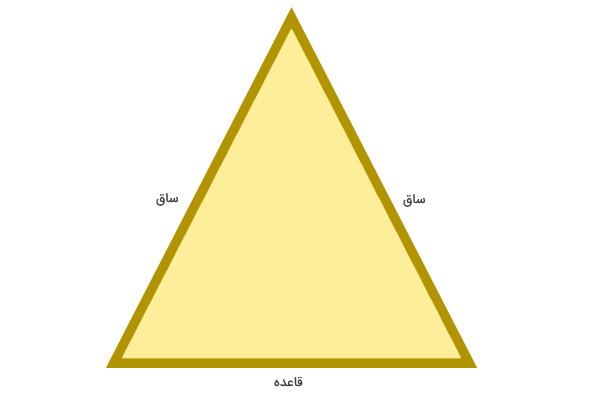
محیط مثلث متساوی الساقین چیست ؟

محیط مثلث متساوی الساقین، جمع اندازه ساق‌ها و قاعده آن است. مثلث متساوی الساقین (الف ب پ) را در نظر بگیرید. یک مثلث، مشابه (الف ب پ) رسم کنید.

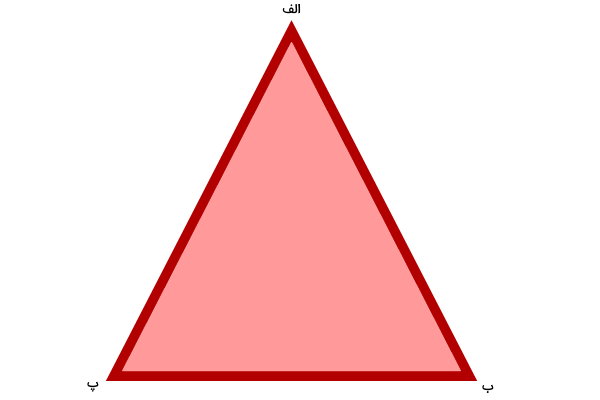
قلم خود را بر روی گوشه (الف) قرار دهید و یک پاره خط از این گوشه به گوشه (ب) بکشید.

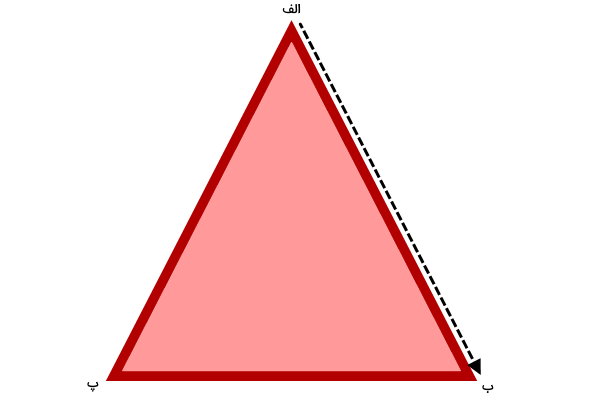
پاره خط دوم را از گوشه (ب) تا گوشه (پ) و پاره خط سوم را از گوشه (پ) به گوشه (الف) رسم کنید.

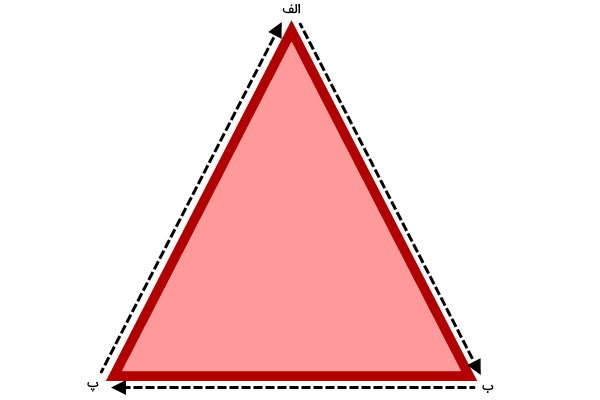
هر یک از این سه پاره خط، بخشی از محیط مثلث متساوی الساقین را نمایش می‌‌دهند. طول هر پاره خط (ضلع مثلث) را با خط کش اندازه‌گیری کرده و با هم جمع کنید. عدد به دست آمده، محیط مثلث است. این رابطه به صورت زیر نوشته می‌شود:

طول (الف ب) + طول (ب پ) + طول (پ الف) = محیط مثلث

ضلع‌های (الف ب) و (الف پ)، ساق و ضلع (ب پ)، قاعده مثلث (الف ب پ) هستند. بنابراین، می‌توانیم رابطه بالا را به صورت زیر بنویسیم:

ساق + قاعده + ساق = محیط مثلث متساوی الساقین

شکل دیگر این رابطه را در بخش‌های بعدی معرفی می‌کنیم.

مثال 1: اندازه گیری محیط مثلث

طول ضلع‌های یک مثلث را با خط‌کش اندازه‌گیری کردیم. پس از رسم مثلث، شکل زیر به دست آمد.

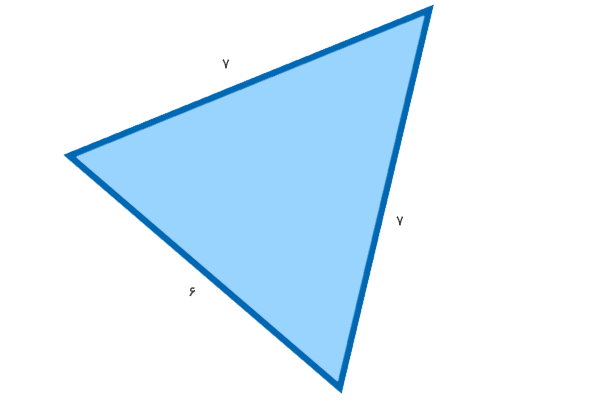
با توجه به تصویر بالا، به سوالات زیر پاسخ دهید:

• این مثلث، از چه نوعی است؟ چرا؟
• محیط مثلث چقدر است؟

مثلث بالا از نوع متساوی الساقین است؛ چراکه این مثلث، دو ضلع برابر دارد. محیط مثلث از رابطه زیر به دست می‌آید:

ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث

7 + 6 + 7 = محیط مثلث

7 + 13 = محیط مثلث

20 = محیط مثلث

در نتیجه، محیط مثلث متساوی الساقین برابر 20 است.

محیط مثلث متساوی الساقین چگونه حساب می شود ؟

در مثلث متساوی الساقین، محیط با جمع دو ساق و قاعده حساب می‌شود. به همین دلیل، رابطه مخصوص محیط مثلث متساوی الساقین را می‌توان به صورت زیر نوشت:

قاعده + (ساق × 2) = محیط مثلث متساوی الساقین

مثال 2: تعیین محیط مثلثی با دو ضلع مساوی

محیط مثلث متساوی الساقین زیر را حساب کنید.

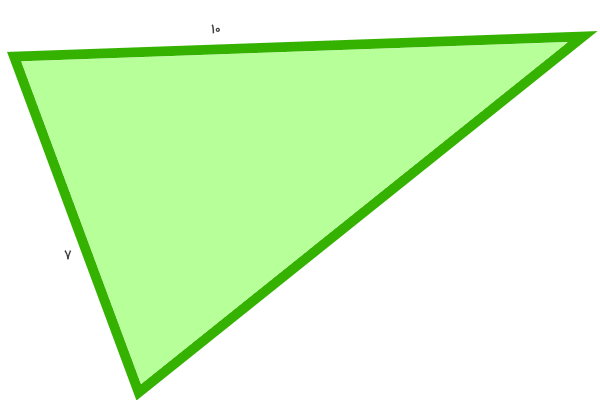
بر اساس تصویر بالا، می‌توان تشخیص داد که اندازه ساق برابر 10 و اندازه قاعده برابر 7 است. رابطه محیط مثلث متساوی الساقین را می‌نویسیم و این اندازه‌ها را درون آن قرار می‌دهیم:

قاعده + (ساق × 2) = محیط مثلث متساوی الساقین

7 + (10 × 2) = محیط مثلث متساوی الساقین

7 + (20) = محیط مثلث متساوی الساقین

27 = محیط مثلث متساوی الساقین

در نتیجه، محیط مثلث متساوی الساقین برابر 27 است.

فرمول محیط مثلث متساوی الساقین چیست ؟

مثلث متساوی الساقین ABC را در نظر بگیرید. اندازه هر ضلع این مثلث را با حروف انگلیسی در کنار آن ضلع نوشته‌ایم.

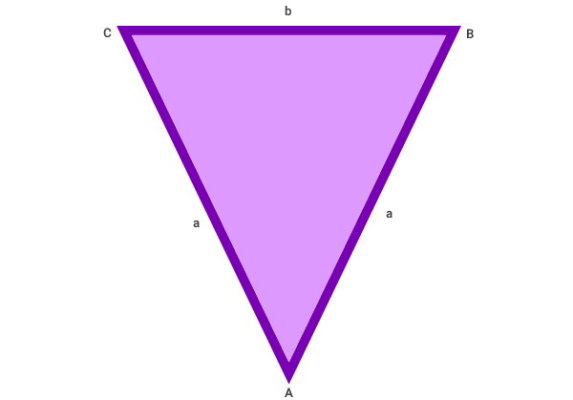
دو ضلع مثلث بالا را با a نشان می‌دهیم؛ چراکه این مثلث از نوع متساوی الساقین بوده و اندازه ساق‌های آن با هم برابر هستند. محیط مثلث بالا با استفاده از رابطه زیر محاسبه می‌شود:

ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث

به جای هر ضلع، عبارت انگلیسی مربوط به آن را در رابطه قرار می‌دهیم:

a + b + a = محیط مثلث

فرمول محیط مثلث ABC برابر است با:

$$
P = a + b + a
$$

• P: محیط مثلث
• a: اندازه ضلع AB و AC
• b: اندازه ضلع BC

در نتیجه، فرمول محیط مثلث متساوی الساقین با عبارت جبری را می‌توان به صورت زیر نوشت:

$$
P = 2a + b
$$

مثال 3: محاسبه محیط مثلث متساوی الساقین با فرمول

محیط یک مثلث متساوی الساقین با ساق 5 سانتی‌متر و قاعده 9 سانتی‌متر را به کمک فرمول حساب کنید.

محیط مثلث متساوی الساقین با استفاده از فرمول زیر محاسبه می‌شود:

$$
P = 2a + b
$$

• P: محیط مثلث متساوی الساقین
• a: اندازه ساق برابر 5 سانتی‌‌متر
• b: اندازه قاعده برابر 9 سانتی‌متر

اندازه ساق‌ها و قاعده را درون فرمول بالا قرار می‌دهیم و آن را حل می‌کنیم:

$$
P = 2a + b
$$

$$
P = (2 \times 5) + 9
$$

$$
P = (10) + 9
$$

$$
P = 19
$$

در نتیجه، محیط مثلث برابر با 19 سانتی‌متر است.

حل مثال محیط مثلث متساوی الساقین

در این بخش، چند مثال دیگر را در زمینه محیط مثلث‌های متساوی الساقین حل می‌کنیم.

مثال 4: محاسبه محیط مثلث متساوی الساقین به دو روش

محیط مثلث زیر را به روش جمع ضلع‌ها و فرمول مخصوص محیط مثلث متساوی الساقین حساب کنید.

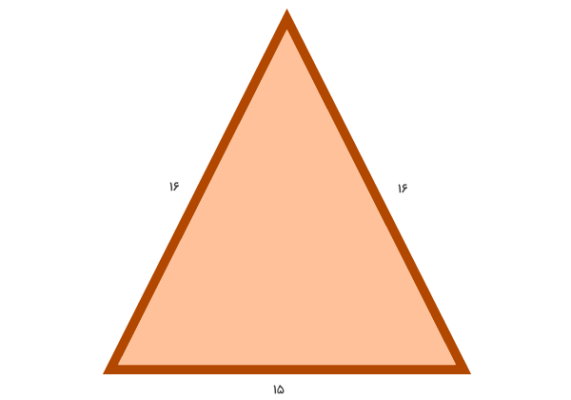
روش کلی محاسبه محیط تمام مثلث‌ها، جمع هر یک از ضلع‌ها است:

ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث

16 + 15 + 16 = محیط مثلث

16 + 31 = محیط مثلث

47 = محیط مثلث

در روش دوم، فرمول مخصوص محیط مثلث‌های متساوی الساقین را می‌نویسیم:

$$
P = 2a + b
$$

• P: محیط مثلث متساوی الساقین
• a: اندازه ساق برابر 16
• b: اندازه قاعده برابر 15

اندازه ساق‌ها را درون فرمول قرار می‌دهیم و آن را حل می‌کنیم:

$$
P = (2 \times 16) + 15
$$

$$
P = (32) + 15
$$

$$
P = 47
$$

در نتیجه، محیط مثلث برابر 47 است.

مثال 5: محاسبه اندازه ساق از روی محیط و قاعده

یک مثلث متساوی الساقین با محیط 30 سانتی‌متر را در نظر بگیرید. اگر اندازه قاعده این مثلث برابر 8 سانتی‌متر باشد، اندازه هر ساق آن چقدر است؟

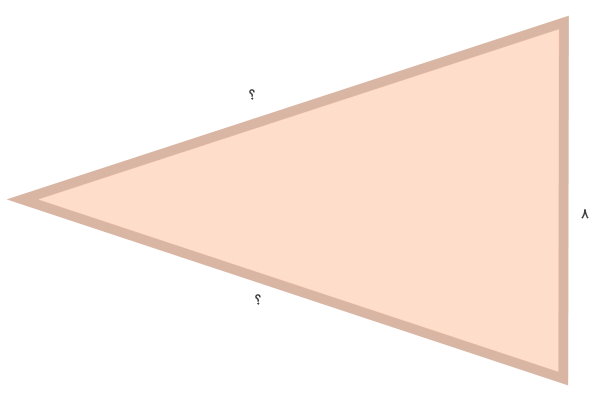
اندازه قاعده و محیط مثلث بالا را داریم. این اندازه‌ها را درون رابطه محیط مثلث متساوی الساقین قرار می‌دهیم:

قاعده + (ساق × 2) = محیط مثلث متساوی الساقین

8 + (ساق × 2) = 30

اکنون رابطه بالا را بر حسب ساق حل می‌کنیم:

30 = 8 + (ساق × 2)

8 - 30 = (ساق × 2)

22 = (ساق × 2)

2 ÷ 22 = ساق

11 = ساق

در نتیجه، اندازه ساق مثلث برابر 11 سانتی‌متر است.

مثال 6: مقایسه محیط مثلث های مختلف

تصویر زیر، سه مثلث مختلف الاضلاع، متساوی الساقین و متساوی الاضلاع را نمایش می‌دهد. محیط هر یک از مثلث‌ها را حساب کرده و با هم مقایسه کنید.

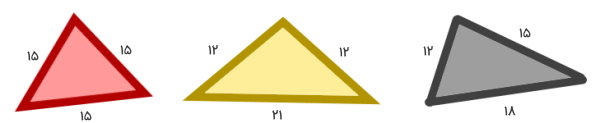
محیط هر یک از مثلث‌های بالا را مطابق با رابطه مخصوص آن‌ها به دست می‌آوریم. رابطه محیط مثلث مختلف الاضلاع (مثلثی با سه ضلع متفاوت) برابر است با:

ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث مختلف الاضلاع

18 + 15 + 12 = محیط مثلث مختلف الاضلاع

45 = محیط مثلث مختلف الاضلاع

محیط مثلث متساوی الساقین به صورت زیر محاسبه می‌شود:

قاعده + (ساق × 2) = محیط مثلث متساوی الساقین

21 + (12 × 2) = محیط مثلث متساوی الساقین

21 + (24) = محیط مثلث متساوی الساقین

45 = محیط مثلث متساوی الساقین

محیط مثلث متساوی الاضلاع نیز با استفاده از رابطه زیر به دست می‌آید:

اندازه یک ضلع × 3 = محیط مثلث متساوی الاضلاع

15 × 3 = محیط مثلث متساوی الاضلاع

45 = محیط مثلث متساوی الاضلاع

محیط هر مثلث با هم برابر است. از این مثال می‌توان نتیجه گرفت که مثلث‌های مختلف با اندازه ضلع‌های متفاوت می‌توانند دارای محیط مساوی باشند.

محاسبه آنلاین محیط مثلث متساوی الساقین

یکی از روش‌های محاسبه محیط مثلث‌های متساوی الساقین، استفاده از سایت‌های اینترنتی است. از سایت‌های مفید در این زمینه می‌توان به موتور جستجوی گوگل و سایت Omnicalculator (+) اشاره کرد.

اگر در سایت گوگل، عبارتی مانند «isosceles triangle perimeter» را جستجو کنید، یک کادر مشابه تصویر زیر به نمایش در می‌آید.

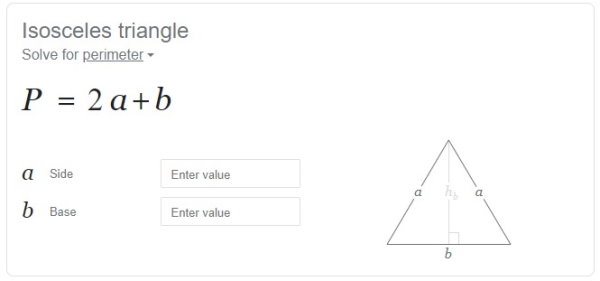
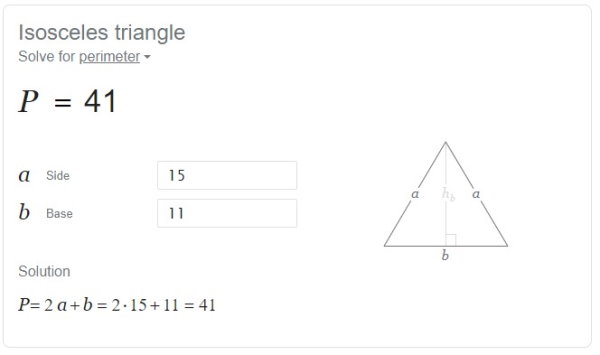
در ماشین حساب گوگل، با وارد کردن اندازه ساق در کادر مقابل عنوان «a Side» و اندازه قاعده در کادر مقابل عنوان (b Base)، محیط مثلث متساوی الساقین محاسبه می‌شود. به عنوان مثال، اندازه‌های مثلثی با ساق 15 و قاعده 11 را در این ماشین حساب وارد می‌کنیم. تصویر زیر، نتیجه محاسبه محیط این مثلث است.

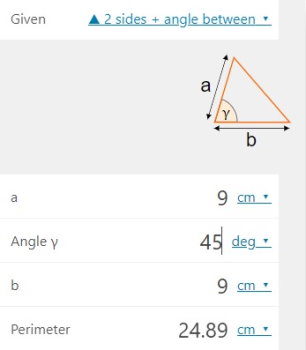
ماشین حساب سایت Omnicalculator (+)، امکان محاسبه محیط مثلث‌های متساوی الساقین با اندازه دو ضلع و زاویه بین یا دو زاویه و ضلع بین را فراهم می‌کند. تصویر زیر، نمونه‌ای از محاسبه محیط مثلث متساوی الساقین با دو ضلع و زاویه بین را نمایش می‌دهد.

سوالات متداول در رابطه با مثلث متساوی الساقین و محیط آن

در این بخش، به برخی از سوالات پرتکرار در رابطه با محیط مثلث‌های متساوی الساقین پاسخ می‌دهیم.

تعریف محیط مثلث متساوی الساقین چیست ؟

محیط مثلث متساوی الساقین، اندازه دور آن است.

محیط مثلث متساوی الساقین چگونه بدست می آید ؟

محیط مثلث متساوی الساقین از جمع اندازه دو ساق با اندازه قاعده به دست می‌آید.

رابطه محیط مثلث متساوی الساقین چیست ؟

رابطه محیط مثلث متساوی الساقین به صورت «قاعده + (ساق × 2)» نوشته می‌شود.

عبارت جبری محیط مثلث متساوی الساقین چیست ؟

فرمول ریاضی یا عبارت جبری محیط مثلث متساوی الاضلاع، به صورت P=2a+b نوشته می‌شود. a، اندازه ساق و b، اندازه قاعده را نمایش می‌دهد.