مستطیل چیست؟ — تعریف و مفاهیم به زبان ساده + فیلم آموزش رایگان

در آموزشهای قبلی مجله فرادرس، با برخی اشکال هندسی مانند دایره، مثلث و مربع آشنا شدیم. در این آموزش، با مستطیل آشنا میشویم که یکی دیگر از شکلهای مهم در هندسه است.
فیلم آموزشی مستطیل و محاسبات آن
مستطیل چیست؟
«مستطیل» (Rectangle) چهارضلعی مسطحی است که دارای دو جفت ضلع است و هر چهار زاویه داخلی آن قائمه (۹۰ درجه) هستند.
شکل زیر یک مستطیل را نشان میدهد.
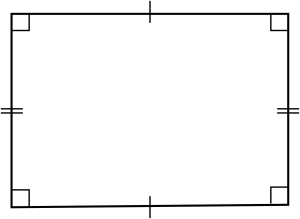
در شکل بالا، ![]() نشانه زاویه قائمه و
نشانه زاویه قائمه و ![]() و
و ![]() نشانه اضلاع مساوی هستند.
نشانه اضلاع مساوی هستند.
بنابراین، شکلی را مستطیل میگوییم که ویژگیهای زیر را داشته باشد:
- دارای چهار ضلع باشد.
- تمام زوایای داخلی آن برابر 90⁰ باشد.
- طول اضلاع روبهرو با یکدیگر مساویاند.
نکته: مربع یک نوع مستطیل است و خود مستطیل نوع خاصی از یک متوازیالاضلاع است.
ویژگیهای مستطیل
ضلع کوچک مستطیل را عرض مستطیل مینامیم و معمولاً با حرف اول معادل انگلیسی آن، یعنی نشان میدهیم.
همچنین، ضلع بزرگ را طول مینامیم و معمولاً با نشان میدهیم. قطر مستطیل نیز، پارهخطی است که دو رأس مقابل را به هم متصل میکند. طول، عرض و قطر مستطیل در شکل زیر نشان داده شدهاند.
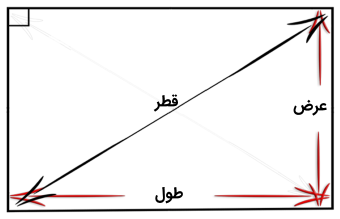
قطر مستطیل
همانطور که گفتیم، قطر یک پارهخط است که دو رأس مقابل یک مستطیل را به هم وصل میکند. هر مستطیل دو قطر دارد که در شکل زیر نشان داده شده است.

دو قطر مستطیل هماندازه هستند و یکدیگر را در مرکز قطع میکنند. زمانی که یک قطر مستطیل را رسم کنیم، مستطیل تبدیل به دو مثلث قائمالزاویه میشود که قطر مستطیل، وتر آن مثلث است. بنابر قضیه فیثاغورس میتوان طول وتر مثلث یا همان قطر مستطیل را محاسبه کرد. اندازه قطر برابر است با مجذورِ مجموعِ مربعِ طول و مربعِ عرض:
(²عرض+²طول)√ = قطر
به عبارت دیگر، اگر اندازه طول ، اندازه عرض و اندازه قطر باشد، با توجه به اینکه طول و عرض بر هم عمود هستند و همراه با قطر یک مثلث قائمالزاویه را تشکیل میدهند، میتوان نوشت:
رسم مستطیل
برای رسم مستطیل به نقاله، خطکش و مداد نیاز داریم. با استفاده از نقاله، میتوان زاویه را اندازه گرفت. با کمک خطکش نیز میتوان خطوط را رسم کرد و طول خطوط را اندازه گرفت. برای رسم مستطیل، پارهخطی به طول دلخواه مورد نظرتان رسم کنید. مثلاً ابتدا یک خط افقی را به عنوان طول مستطیل رسم کنید. اکنون مرکز نقاله را روی دو انتهای پارهخط گذاشته و زاویه ۹۰ درجه را تعیین و با مدار مشخص کنید.

در مرحله بعد، خطکش را بهگونهای قرار دهید که نقطه ابتدایی آن، یکی از نقطا انتهایی پارهخط و نقطه دیگر آن، نقطهای باشد که با زاویه ۹۰ درجه توسط نقاله مشخص کردهاید. پارهخطی به اندازه عرض مورد نظر رسم کنید. همین کار را برای دو نقطه دیگر در سمت دیگر پارهخط انجام دهید. اکنون سه ضلع داریم. ضلع دیگر را رسم کرده و شکل را تکمیل کنید.
مساحت مستطیل
مساحت مستطیل برابر است با حاصلضرب طول در عرض آن:
طول × عرض = مساحت
به عبارت دیگر، اگر طول برابر با و عرض برابر با باشد، مساحت مستطیل به صورت زیر خواهد بود:
برای آشنایی بیشتر با نحوه محاسبه مساحت مستطیل میتوانید مطلب «مساحت مستطیل — به زبان ساده (+ فیلم آموزش رایگان)» را در این لینک مطالعه کنید.
محیط مستطیل
محیط مسیری است که سطح یک شکل را احاطه میکند. محیط یک مستطیل نیز برابر با مجموع اندازه چهار ضلع آن است. از انجا که دو عرض و دو طول مستطیل برابر هستند، میتوان به صورت سادهتر گفت که محیط مستطیل برابر است با مجموع طول و عرض، ضرب در 2:
(طول + عرض) × 2 = محیط
یعنی اگر طول برابر با و عرض باشد، محیط مستطیل برابر خواهد بود با:
برای آشنایی کامل با نحوه محاسبه محیط مستطیل پیشنهاد میکنیم مطلب «محیط مستطیل و محاسبه آن — به زبان ساده (+ فیلم آموزش رایگان)» را در این لینک مطالعه کنید.
مثالهای مستطیل
در این بخش، چند مثال را درباره مستطیل حل میکنیم.
مثال اول مستطیل
مساحت مستطیلی با 6 متر طول و 3 متر عرض چقدر است؟
حل: طول و عرض را داریم. مساحت برابر است با حاصلضرب طول در عرض:
مثال دوم مستطیل
مستطیلی دارای 12 سانتیمتر طول و 5 سانتیمتر عرض است. محیط مستطیل را حساب کنید.
حل: با داشتن طول و عرض ، محیط مستطیل برابر است با:
مثال سوم مستطیل
مستطیلی با ابعاد 12 سانتیمتر و 5 سانتیمتر داریم. اندازه قطر آن چقدر است؟
حل: از رابطهای که در بالا گفتیم، استفاده میکنیم و قطر را به دست میآوریم:
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش های بدست آوردن محیط و مساحت مستطیل + حل تمرین و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مستطیل چیست ؟ — تعریف و مفاهیم به زبان ساده + فیلم آموزش رایگان(همین مطلب)
- طول و عرض مستطیل چیست و چگونه بدست می آید ؟ + حل تمرین و مثال
- قطر مستطیل چیست و چه خواصی دارد؟ — فرمول های محاسبه + حل مثال
- محیط مستطیل چگونه بدست می آید؟ + فیلم آموزشی و حل تمرین و مثال
- مساحت مستطیل به زبان ساده + فیلم آموزشی و حل تمرین
- حجم مکعب مستطیل چیست ؟ — به زبان ساده + حل تمرین و مثال های متنوع
- رابطه محیط و مساحت مستطیل — معرفی فرمول ها + حل تمرین و مثال
- فرمول محیط مستطیل چیست ؟ — به زبان ساده + حل مثال
- فرمول مساحت مستطیل چیست ؟ — به زبان ساده + حل مثال
- محیط مستطیل به صورت جبری — فرمول های محیط مستطیل + حل تمرین و مثال
- مساحت مستطیل به صورت جبری — فرمول های ریاضی + حل مثال
- محیط مستطیل کسری چگونه بدست می آید ؟ + حل تمرین و مثال
- مساحت مستطیل کسری چگونه بدست می آید ؟ — حل تمرین و مثال













سلام ببخشید زاویه هایی که قطر با زاویه قائمه می سازه چقدر است ؟؟
سلام.
زاویهای که قطر با اضلاع مستطیل میسازد به اندازه اضلاع وابسته است. برای محاسبه زاویه میتوانید از روابط مثلثاتی کمک بگیرید. پیشنهاد میکنیم مطلب «سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» را مطالعه کنید.
سالم و موفق باشید.
سلام اگر طول قطر مستطیل و زاویه بین قطرها را داشته باشیم مساحت مستطیل را چگونه حساب کنیم
سلام
اگه ما *قطر* و *عرض* مستطیل رو داشته باشیم چطور طولش رو بدس میاریم ؟؟؟
سلام.
در بخش «قطر مستطیل» هیمن مطلب رابطه ریاضی بین طول و عرض و قطر مستطیل را نوشتهایم. از این رابطه استفاده کنید.
موفق باشید.
باسلام
مسئله : مساحت مستطیلی برابر۲۴وطول وعرض ان چقدر میشود چگونه بدست اوریم
سلام چرا طول و عرض تو این مطلب جابه جا هستش؟
سلام. اصلاحات لازم انجام شد. از توجه و دقت شما سپاسگزاریم.
[…] مستطیل و محاسبات آن — به زبان ساده – وبلاگ فرادرس […]