مجموع زوایای خارجی چند ضلعی محدب چیست؟ — به زبان ساده + حل مثال
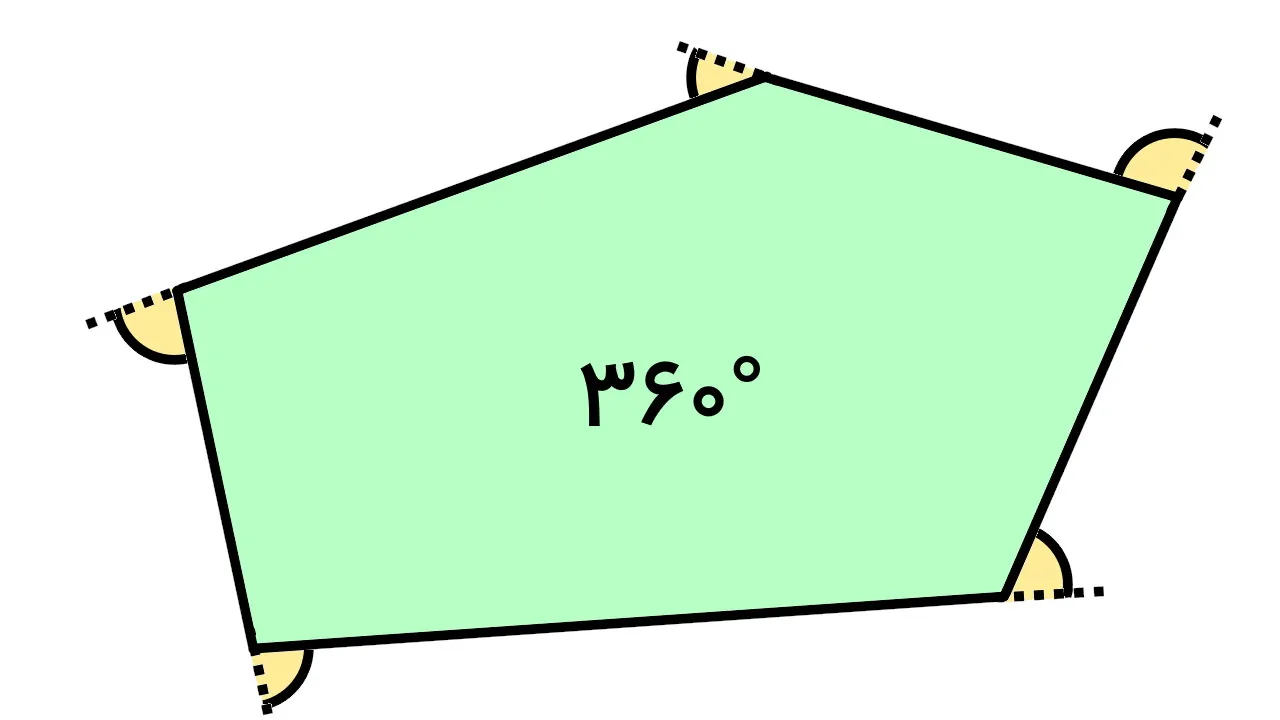
مجموع زوایای خارجی چند ضلعی محدب همواره برابر با ۳۶۰ درجه است. این عدد، ارتباطی به منتظم یا غیر منتظم بودن، تعداد ضلعها و حتی تعداد راسهای چندضلعی محدب ندارد. در این مقاله، نحوه محاسبه مجموع زوایای خارجی چند ضلعی محدب و اثبات آن را به همراه حل مثال آموزش میدهیم.
چند ضلعی محدب چیست؟
به یک چندضلعی با زاویههای داخلی کوچکتر از ۱۸۰ درجه، چندضلعی محدب میگویند. اگر حتی زاویه یکی از راسهای چندضلعی، بیشتر از ۱۸۰ درجه باشد، آن چند ضلعی، غیر محدب (چندضلعی مقعر) محسوب میشود.
تصویر زیر زوایای خارجی و داخلی مثلث (کوچکترین چندضلعی محدب) را نمایش میدهد.
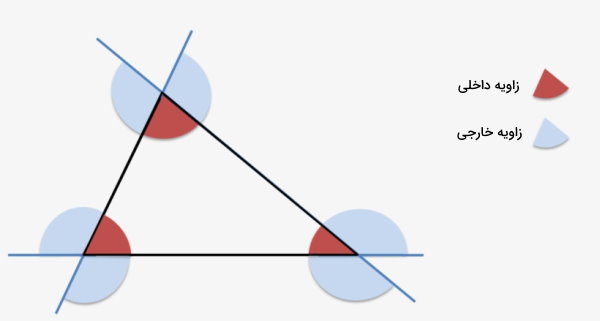
زاویه خارجی چند ضلعی محدب چیست؟
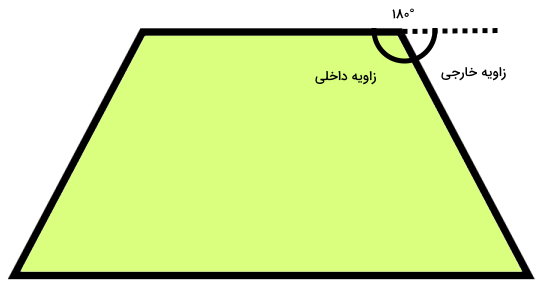
زاویه بین یک ضلع و امتداد ضلع مجاور آن، با عنوان «زاویه خارجی» شناخته میشود. زاویههای داخلی و خارجی مجاور در یک چند ضلعی محدب، مکمل یکدیگر هستند.
به عبارت دیگر، حاصلجمع هر دو زاویه داخلی و خارجی متناظر، برابر با ۱۸۰ درجه است. این ویژگی، به منظور اثبات مجموع زوایای خارجی چند ضلعی محدب مورد استفاده قرار میگیرد.
مجموع زوایای خارجی چند ضلعی محدب چگونه بدست می آید ؟
مجموع زوایای خارجی چند ضلعی محدب برابر ۳۶۰ درجه است. این عدد، با استفاده از قانون جمع زاویههای خارجی و داخلی مجاور به دست میآید.
به عنوان مثال، مثلث متساویالاضلاع زیر را در نظر بگیرید. در این مثلث، تمام زاویههای داخلی برابر با ۶۰ درجه هستند.
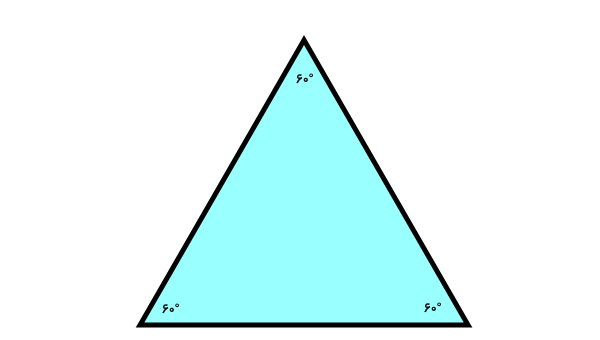
مثلث بالا، سه زاویه خارجی دارد. این زاویهها، بین امتداد هر ضلع با ضلع مجاورش قرار دارند.
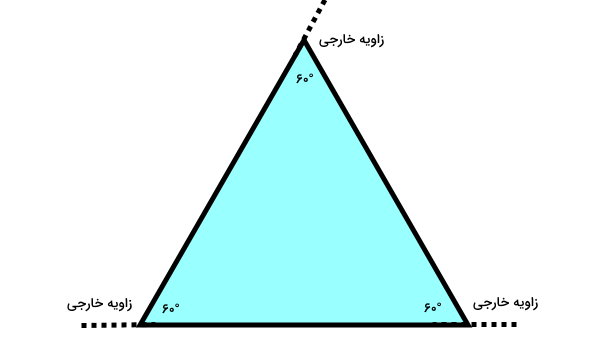
رابطه بین زاویه خارجی و داخلی مجاور عبارت است از:
۱۸۰° = زاویه خارجی + زاویه داخلی
بر اساس رابطه بالا، یکی از زاویههای خارجی مثلث متساویالاضلاع، به صورت زیر محاسبه میشود:
۱۸۰° = زاویه خارجی + °۶۰
۶۰° - ۱۸۰° = زاویه خارجی
۱۲۰° = زاویه خارجی
تمام زوایای داخلی مثلث متساویالاضلاع هماندازه هستند. بنابراین، دو زاویه خارجی دیگر نیز برابر با ۱۲۰ درجه خواهند بود.
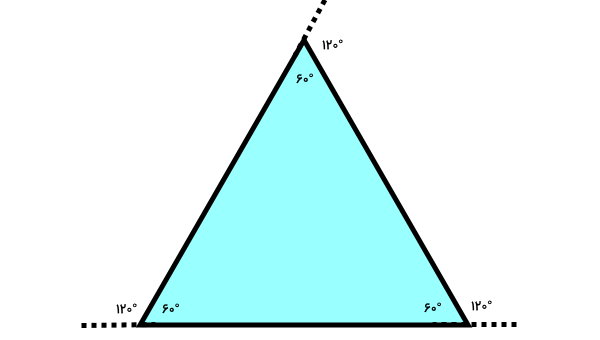
مجموع زوایای خارجی چند ضلعی محدب بالا برابر است با:
۱۲۰° + ۱۲۰° + ۱۲۰° = مجموع زوایای خارجی
۳۶۰° = مجموع زوایای خارجی
همانطور که مشاهده میکنید، مجموع زوایای خارجی چند ضلعی محدب با سه ضلع و زاویه مساوی، برابر با ۳۶۰ درجه شد. این عدد برای چهارضلعی، پنجضلعی، ششضلعی و دیگر انواع چندضلعیهای محدب، تغییری نخواهد کرد.
مثال ۱: محاسبه مجموع زوایای خارجی مربع
مجموع زوایای خارجی یک مربع دلخواه را به دست بیاورید.
مربع، یک چهارضلعی محدب است که از چهار راس با زاویه راست (۹۰ درجه) تشکیل میشود. به منظور محاسبه مجموع زوایای خارجی مربع، شکل آن را رسم میکنیم. سپس اندازه زاویههای داخلی آن را در کنار راسٰها مینویسیم.
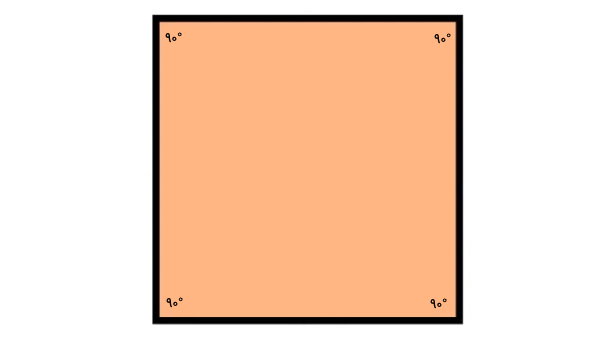
زاویه خارجی هر راس، در میان امتداد یکی از ضلعهای آن راس با ضلع مجاورش قرار دارد.
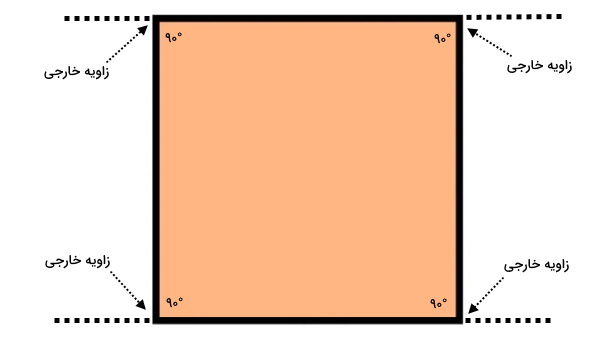
اندازه هر زاویه خارجی برابر است با:
۱۸۰° = زاویه خارجی + زاویه داخلی
زاویه داخلی - °۱۸۰ = زاویه خارجی
۹۰° - ۱۸۰° = زاویه خارجی
۹۰° = زاویه خارجی
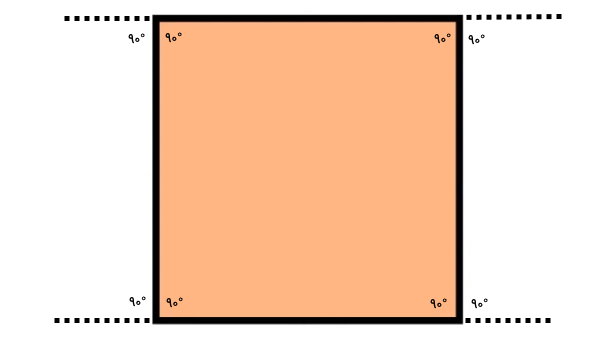
مربع، چهار زاویه خارجی دارد. بنابراین، مجموع زوایای خارجی آن به صورت زیر محاسبه میشود:
۹۰° + ۹۰° + ۹۰° + ۹۰° = مجموع زوایای خارجی
۳۶۰° = مجموع زوایای خارجی
در نتیجه، مجموع زوایای خارجی مربع نیز مانند مجموع زوایای خارجی مثلث، برابر با ۳۶۰ درجه شد. مثلث متساویالاضلاع و مربع، از چندضلعیهای محدب منتظم هستند. این چندضلعیها، ضلعهای مساوی و زاویههای برابر دارند. در مثال بعدی، مجموع زوایای خارجی چند ضلعی محدب غیر منتظم را حل میکنیم.
مثال ۲: محاسبه مجموع زوایای خارجی چهارضلعی محدب
شکل زیر، یک چهارضلعی محدب غیر منتظم را نمایش میدهد. دو زاویه داخلی و دو زاویه خارجی این چهارضلعی معلوم هستند. مجموع زوایای خارجی را حساب کنید.
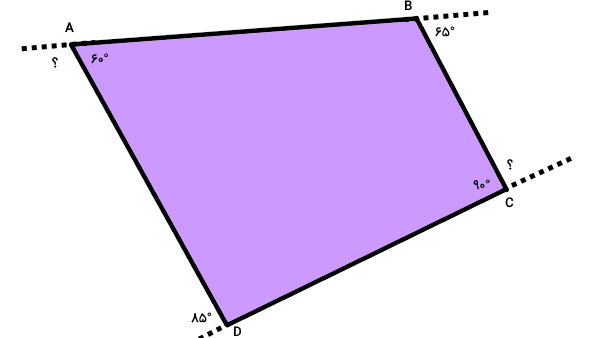
زوایای خارجی راسهای B و D را داریم. به منظور محاسبه مجموع زوایای خارجی، باید زوایای خارجی راسهای A و C را نیز به دست بیاوریم. این مقادیر از روی زوایای داخلی تعیین میشوند:
۱۸۰° = زاویه خارجی A + زاویه داخلی A
۱۸۰° = ۶۰° + زاویه خارجی A
۶۰° - ۱۸۰° = زاویه خارجی A
۱۲۰° = زاویه خارجی A
۱۸۰° = زاویه خارجی C + زاویه داخلی C
۱۸۰° = ۹۰° + زاویه خارجی C
۹۰° - ۱۸۰° = زاویه خارجی C
۹۰° = زاویه خارجی C
اکنون، تمام زوایای خارجی را با هم جمع میکنیم:
۸۵° + ۹۰° + ۶۵° + ۱۲۰° = مجموع زوایای خارجی
۳۶۰° = مجموع زوایای خارجی
مجموع زوایای خارجی چند ضلعی محدب با ضلعها و زاویههای نابرابر نیز مانند چندضلعیهای منتظم برابر با ۳۶۰ درجه شد.
اثبات مجموع زوایای خارجی چند ضلعی محدب
یکی از روشهای اثبات مجموع زوایای خارجی چند ضلعی محدب، استفاده از فرمول مجموع زوایای داخلی است. بر اساس این فرمول، جمع زاویههای داخلی تمام چندضلعیها برابر است با:
- S: مجموع زوایای داخلی
- n: تعداد ضلعها
پنجضلعی زیر را در نظر بگیرید. اندازه هیچیک از زاویههای داخلی و خارجی این پنجضلعی معلوم نیستند. با این حال، امکان محاسبه مجموع زوایای خارجی آن وجود دارد.
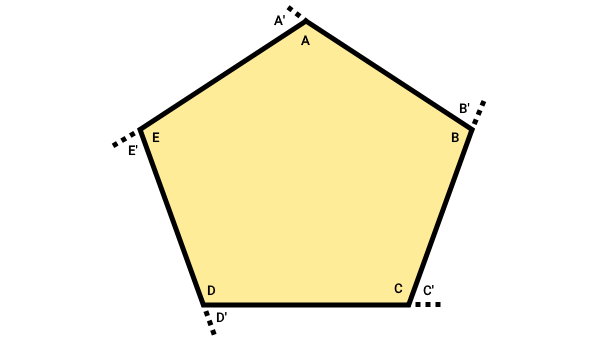
مجموع زاویه داخلی و خارجی هر راس برابر با ۱۸۰ درجه است:
بنابراین، مجموع تمام زوایای داخلی و خارجی پنجضلعی برابر است با:
همانطور که مشاهده میکنید، مجموع تمام زوایای داخلی و خارجی یک n ضلعی، برابر با ۱۸۰n است. در رابطه بالا، عبارتهای مربوط به زاویه داخلی و عبارتهای مربوط به زاویه خارجی را به صورت جداگانه یادداشت میکنیم:
مجموع زوایای خارجی (S)، از رابطه زیر محاسبه میشود:
در نتیجه، مجموع زوایای خارجی ('S) از رابطه زیر به دست میآید:
در نتیجه، مجموع زوایای خارجی هر n ضلعی محدب برابر با ۳۶۰ درجه است. برای آشنایی با نحوه اثبات فرمول مجموع زوایای داخلی چند ضلعی محدب، مطالعه مطلب «مجموع زوایای داخلی چند ضلعی محدب چیست ؟ — به زبان ساده + حل مثال» را به شما پیشنهاد میکنیم.
مثال ۳: تعیین اندازه زاویه خارجی چند ضلعی محدب
زاویه خارجی مجهول را به دست بیاورید.
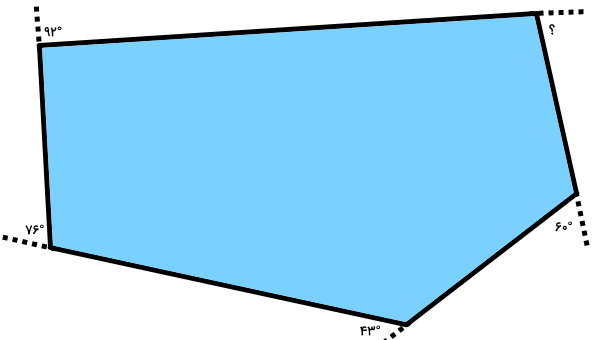
مجموع زوایای خارجی چند ضلعی محدب برابر با ۳۶۰ درجه است. با توجه به تصویر بالا، اندازه چهار زاویه خارجی را داریم. اندازه زاویه خارجی پنجم از رابطه زیر به دست میآید:
۳۶۰° = زاویه خارجی پنجم + جمع چهار زاویه خارجی
جمع چهار زاویه خارجی - °۳۶۰ = زاویه خارجی پنجم
جمع چهار زاویه خارجی برابر است با:
۲۷۱° = ۶۰° + ۴۳° + ۷۶° + ۹۲° = جمع چهار زاویه خارجی
۲۷۱° = جمع چهار زاویه خارجی
بنابراین، برای زاویه خارجی پنجم داریم:
۲۷۱° - ۳۶۰° = زاویه خارجی پنجم
۸۹° = زاویه خارجی پنجم
مجموع زوایای خارجی چند ضلعی محدب منتظم
چند ضلعی منتظم، یکی از انواع چندضلعیهای محدب است که از ضلعهای هماندازه و زاویههای مساوی تشکیل میشود. مجموع زوایای خارجی چند ضلعی محدب منتظم نیز مانند دیگر چندضلعیهای محدب، برابر با 360 درجه است.
تصویر زیر، یک هشتضلعی منتظم با زاویههای داخلی 135 درجه را نمایش میدهد.
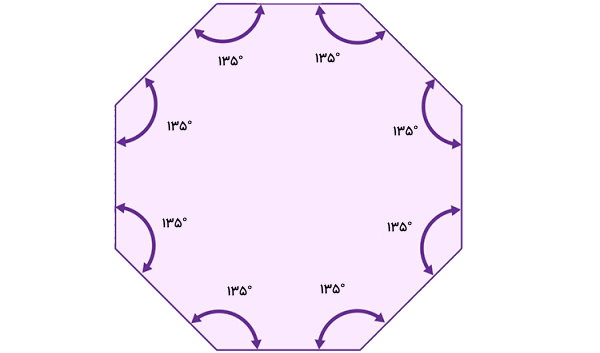
به دلیل برابر بودن زوایای داخلی این چندضلعی، زوایای خارجی آن نیز با یکدیگر برابر هستند. اندازه این زاویهها از رابطه زیر به دست میآید:
۱۸۰° = زاویه خارجی + زاویه داخلی
۱۸۰° = زاویه خارجی + °135
135° - ۱۸۰° = زاویه خارجی
۴۵° = زاویه خارجی
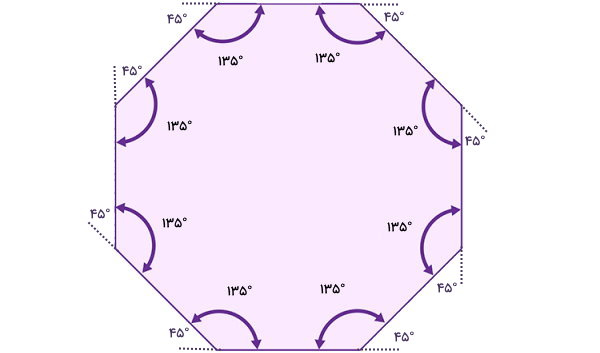
اگر زوایای خارجی هشتضلعی بالا را با هم جمع کنیم، به عدد 360 درجه خواهیم رسید:
360° = ۴۵° + ۴۵° + ۴۵° + ۴۵° + ۴۵° +۴۵° + ۴۵° +۴۵°
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش انواع چند ضلعی ها — تعاریف و تمامی فرمول های محیط و مساحت» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- چند ضلعی چیست ؟ — به زبان ساده
- چند ضلعی محدب چیست ؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده
- چند ضلعی مقعر چیست ؟ — تعریف اجزا، ویژگیها و فرمولها — به زبان ساده
- چند ضلعی منتظم چیست ؟ — به زبان ساده + فیلم آموزش رایگان و حل تمرین
- مجموع زوایای داخلی چند ضلعی محدب چیست ؟ — به زبان ساده + حل مثال
- مجموع زوایای خارجی چند ضلعی محدب چیست ؟ — به زبان ساده + حل مثال(همین مطلب)
- فرمول بدست آوردن مجموع زوایای داخلی چند ضلعی + حل تمرین
- مجموع زوایای چند ضلعی مقعر — به زبان ساده + حل تمرین و اثبات فرمول
- مجموع زوایای خارجی چند ضلعی منتظم — به زبان ساده + اثبات
- مساحت چند ضلعی منتظم چگونه بدست می آید ؟ — به زبان ساده + حل مثال
- محور تقارن چند ضلعی منتظم چیست ؟ — به زبان ساده












