محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان

محیط مثلث از جمع اندازه هر سه ضلع آن به دست میآید. البته این در حالتی است که اندازههای همه ضلعهای مثلث مشخص باشند. به علاوه، در مثلثهایی نظیر مثلث متساوی الساقین، مثلث متساوی الاضلاع و مثلث قائم الزاویه، روابط مخصوص برای محاسبه محیط وجود دارند. در این آموزش از مجله فرادرس، روشها و فرمولهای مورد استفاده برای محاسبه محیط مثلث های مختلف را به همراه حل چندین مثال متنوع و کاربردی توضیح میدهیم.
فیلم آموزشی محیط مثلث
مثلث چیست ؟
در مطلب «مثلث چیست؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)» از مجله فرادرس، مثلث را تعریف کردیم. مثلث، شکلی است که 3 ضلع و 3 گوشه دارد. مثلث به عنوان یکی از شکلهای هندسی پایه محسوب میشود.
بسیاری از شکلهای هندسی و چند ضلعیها را میتوان به مجموعهای از چند مثلث تقسیم کرد. تصویر زیر، ضلعها و گوشههای یک مثلث را نمایش میدهد.
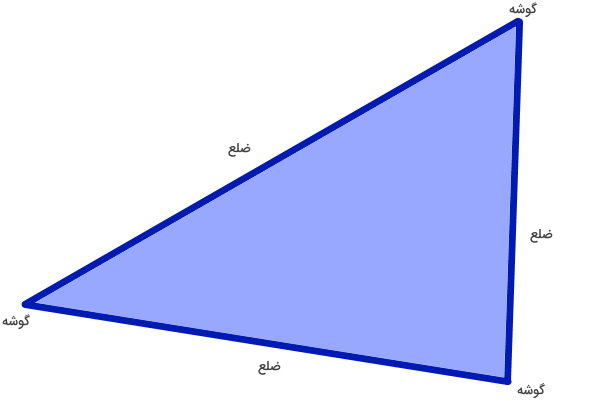
محیط مثلث چیست ؟
اندازه دور هر شکل را محیط آن شکل میگویند. محیط مثلث، اندازه دور آن یا مجموع اندازه ضلعهای تشکیل دهنده آن است.
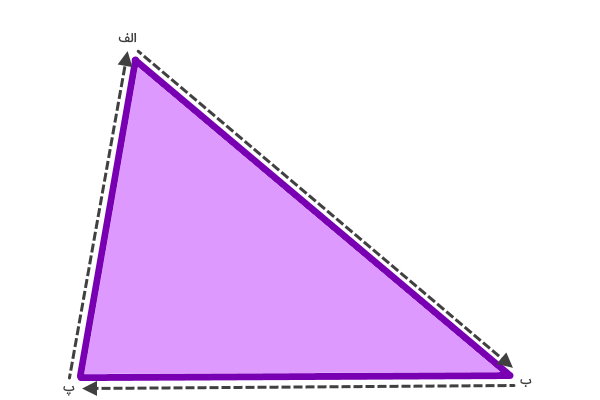
برای یادگیری مفهوم محیط، یک مثلث مانند تصویر را زیر رسم کنید. سپس، قلم خود را بر روی گوشه (الف) قرار داده و آن را بر روی تمام ضلعهای مثلث حرکت دهید. پس از رسیدن به نقطه شروع، قلم به اندازه محیط مثلث حرکت کرده است.
مثال 1: تعیین محیط مثلث
با استفاده از خط کش، طول هر ضلع مثلث زیر را اندازهگیری کردهایم و عدد آن در کنار ضلع نوشتهایم. محیط مثلث چقدر است؟
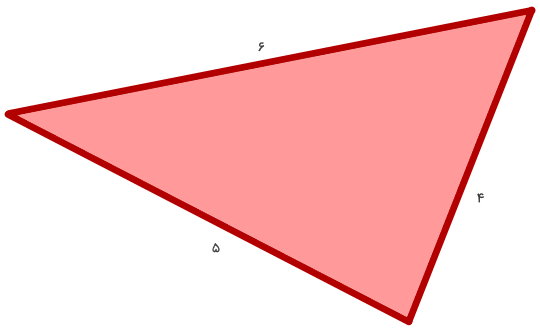
برای تعیین محیط مثلث، باید اندازه هر ضلع آن را با یکدیگر جمع کنیم. بنابراین:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
اندازه ضلع اول برابر 4، اندازه ضلع دوم برابر 5 و اندازه ضلع سوم برابر 6 است. این عددها را در رابطه بالا قرار میدهیم:
6 + 5 + 4 = محیط مثلث
6 + 9 = محیط مثلث
15 = محیط مثلث
در نتیجه، محیط مثلث برابر 15 است.
محیط مثلث چه کاربردی دارد؟
بسیاری از اشیا و مکانهای اطراف ما به شکل مثلث هستند. محیط، برای اندازهگیری طول اطراف این موارد مورد استفاده قرار میگیرد. به عنوان مثال، اگر فردی یک زمین مثلثی شکل داشته و قصد تعیین محدوده دور آن را داشته باشد، باید از فرمول محیط مثلث استفاده کند.
فرمول محیط مثلث چیست ؟
در مثال 1، رابطه کلامی محیط مثلث را بیان کردیم. بر اساس این رابطه، محیط مثلث برابر است با:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
برای بیان فرمول ریاضی مثلث، باید اندازه هر یک از ضلعهای آن را به صورت متغیر (حروف) بیان کنیم. به این منظور، مثلث زیر را در نظر بگیرید.
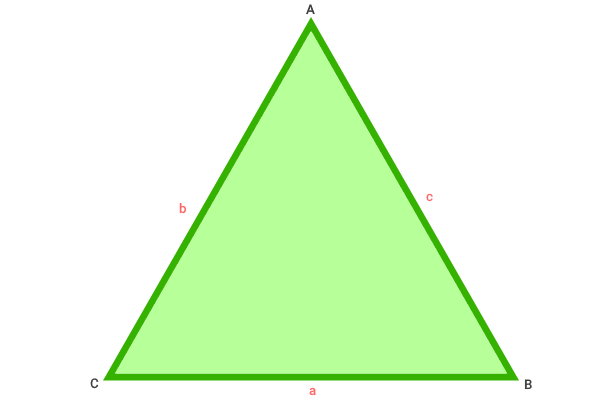
عبارت جبری یا فرمول ریاضی محیط مثلث بالا (مثلث ABC) را میتوان به صورت زیر نوشت:
- P: محیط مثلث
- a: اندازه ضلع BC
- b: اندازه ضلع AC
- c: اندازه ضلع AB
این فرمول، یک رابطه کلی برای تمام انواع مثلثها است. در صورت داشتن اندازه سه ضلع، میتوانید آنها را درون فرمول بالا قرار دهید و محیط مثلث را به دست بیاورید.
واحد محیط مثلث چیست ؟
برای بیان محیط مثلث از واحد طول استفاده میشود. به عنوان مثال، اگر طول ضلعهای مثلث بر اساس سانتیمتر اندازهگیری شود، واحد محیط برابر سانتیمتر خواهد بود.
انواع مثلث چه هستند ؟
مثلثها، تفاوتها و شباهتهای مختلفی دارند. بر اساس تفاوت بین اندازه ضلع و زاویه، انواع مثلث به موارد زیر تقسیم میشوند:
- انواع مثلث بر اساس اندازه زاویه داخلی
- مثلث با زاویه بسته یا حاده (یک زاویه بزرگتر از 90 درجه)
- مثلث با زاویه 90 درجه یا قائم الزاویه
- مثلث با زاویه باز یا منفرجه (سه زاویه کوچکتر از 90 درجه)
- انواع مثلث بر اساس اندازه ضلع
- مثلث مختلف الاضلاع (سه ضلع نامساوی)
- مثلث متساوی الساقین (دو ضلع هم اندازه)
- مثلث متساوی الاضلاع (سه ضلع هم اندازه)
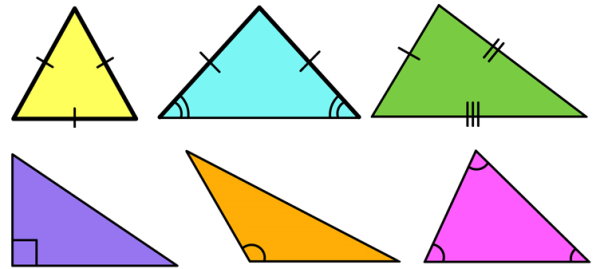
محیط انواع مثلث چگونه بدست می آید ؟
در این بخش، به آموزش نحوه محاسبه محیط انواع مثلث (متساوی الساقین، متساوی الاضلاع، مختلف الاضلاع و قائم الزاویه) به همراه حل چند مثال میپردازیم.
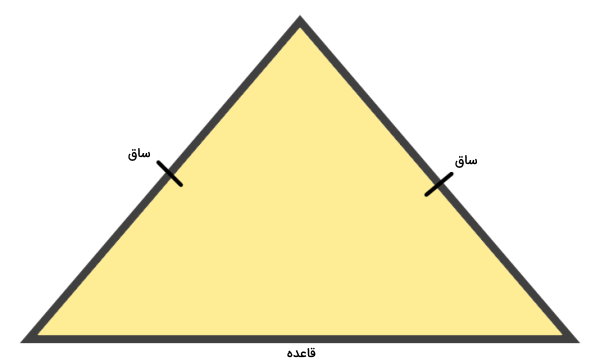
محیط مثلث متساوی الساقین
مثلثی که دو ضلع برابر دارد، به عنوان مثلث متساوی الساقین در نظر گرفته میشود. به ضلعهای برابر این مثلث، «ساق» و به ضلع سوم آن، «قاعده» میگویند. تصویر زیر، نمونهای از یک مثلث متساوی الساقین را نمایش میدهد. علامت | بر روی ساقهای این مثلث، نشانه برابر بودن اندازه آنها است.
مثال 2: محاسبه محیط مثلث با دو ضلع برابر
در مثلث متساوی الساقین زیر، طول پاره خط مشخص شده با علامت ؟ را پیدا کنید. سپس، محیط مثلث را به دست بیاورید.
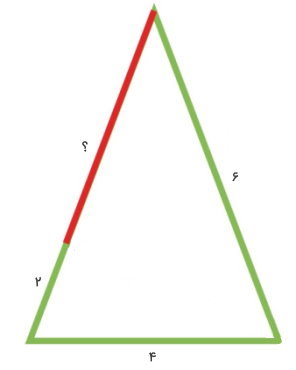
مثلث بالا، مثلث متساوی الساقین با یک ساق به اندازه 6 است. بنابراین، اندازه ساق دیگر مثلث نیز برابر با 6 خواهد بود. طول پاره خط مجهول به صورت زیر محاسبه میشود:
پاره خط مجهول + 2 = ساق مثلث
پاره خط مجهول + 2 = 6
2 - 6 = پاره خط مجهول
4 = پاره خط مجهول
محیط مثلث، از جمع اندازه سه ضلع آن به دست میآید:
6 + 6 + 4 = محیط مثلث
16 = محیط مثلث
در نتیجه، محیط مثلث برابر 16 است.
عبارت جبری محیط مثلث متساوی الساقین
در مثلث متساوی الساقین، اندازه ساق را با a و قاعده را با b نشان میدهند. از آنجایی که اندازه ساقهای این مثلث با هم برابر هستند، برای نشان دادن هر دوی آنها از حرف a استفاده میشود.
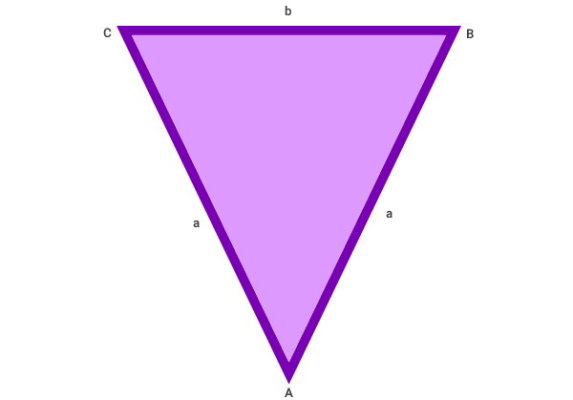
بر اساس تصویر بالا، فرمول ریاضی یا عبارت جبری محیط مثلث متساوی الساقین برابر است با:
- P: محیط مثلث متساوی الساقین
- a: اندازه ساق مثلث
- b: اندازه قاعده مثلث
به دلیل برابر بودن اندازه ساقها (a)، میتوانیم آنها را با هم جمع کنیم و دو ساق را با یک عبارت نشان دهیم:
محیط مثلث متساوی الاضلاع
مثلثی که ضلعهای آن برابرند، با عنوان مثلث متساوی الاضلاع شناخته میشود. مثلث متساوی الاضلاع، یک چند ضلعی منتظم است. تصویر زیر، یک مثلث با سه ضلع برابر را نمایش میدهد. برای نشان دادن برابر بودن ضلعها، معمولا از علامت | بر روی هر سه ضلع مثلث متساوی الاضلاع استفاده میشود.
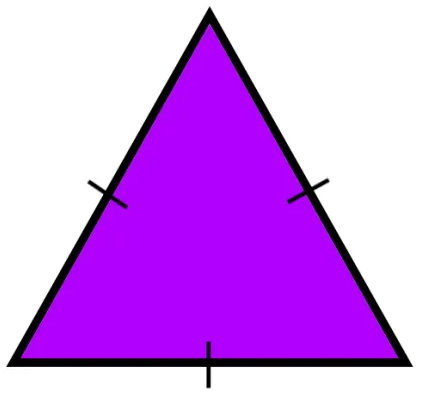
مثال 3: محیط مثلث با سه ضلع برابر
شکل زیر، یک مثلث متساوی الاضلاع است. محیط این شکل را حساب کنید. محیط به دست آمده، چند برابر اندازه یک ضلع است؟
محیط مثلث از رابطه زیر به دست میآید:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
تمام ضلعهای مثلث متساوی الاضلاع برابرند. در نتیجه:
5 + 5 + 5 = محیط مثلث
15 = محیط مثلث
در نتیجه، محیط مثلث متساوی الاضلاع برابر 15 است. برای مشخص کردن اینکه محیط به دست آمده چند برابر اندازه یک ضلع است، باید اندازه محیط (عدد 15) را بر اندازه یک ضلع (عدد 5) تقسیم کنیم:
3 = 5 ÷ 15
بنابراین، محیط مثلث متساوی الاضلاع، 3 برابر اندازه یک ضلع آن است.
عبارت جبری محیط مثلث متساوی الاضلاع
در مثلث متساوی الاضلاع زیر، اندازه هر یک از ضلعها را با a نشان دادهایم.
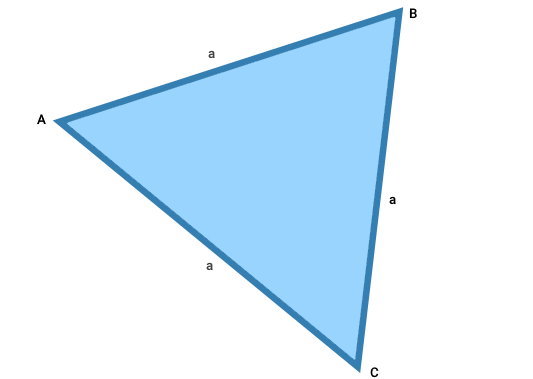
بر اساس تصویر بالا، فرمول ریاضی یا عبارت جبری محیط مثلث متساوی الاضلاع، به صورت زیر نوشته میشود:
- P: محیط مثلث متساوی الاضلاع
- a: اندازه ضلع مثلث
به دلیل برابر بودن اندازه تمام ضلعها، میتوایم فرمول بالا را به صورت زیر بازنویسی کنیم:
محیط مثلث مختلف الاضلاع
مثلث مختلف الاضلاع، مثلثی است که هر سه ضلع آن اندازه های متفاوت دارند. تصویر زیر، نمونهای از یک مثلث مختلف الاضلاع را نمایش میدهد. در برخی از مواقع، به منظور نشان دادن متفاوت بودن اندازه تمام ضلعها، از علامتهای |، || و ||| بر روی ضلعهای این مثلث استفاده میشود.
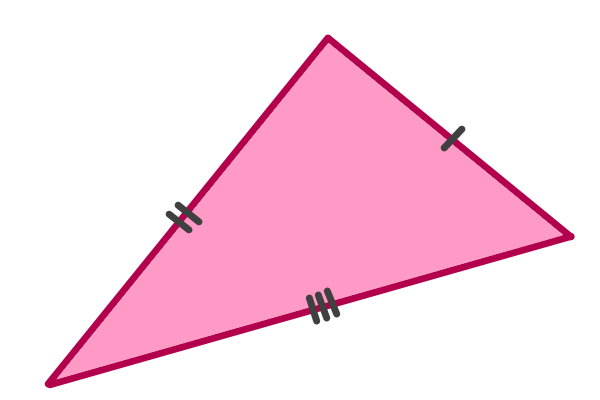
رابطه محیط مثلث مختلف الاضلاع، همان رابطه کلی محیط مثلث است:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
فرمول ریاضی یا عبارت جبری محیط مثلث مختلف الاضلاع نیز با فرمول کلی محیط مثلث تفاوتی ندارد:
- P: محیط مثلث
- a: اندازه ضلع اول
- b: اندازه ضلع دوم
- c: اندازه ضلع سوم
اگر نوع یک مثلث برایتان مشخص نبود یا راهی برای فهمیدن نوع مثلث نداشتید، باید آن را به عنوان یک مثلث مختلف الاضلاع در نظر بگیرید. تمام فرمولهای کلی محیط و مساحت مثلث، برای مثلثهای مختلف الاضلاع قابل استفاده هستند.
مثال 4: محاسبه محیط مثلث با سه ضلع متفاوت
محیط شکل زیر را تعیین کنید.
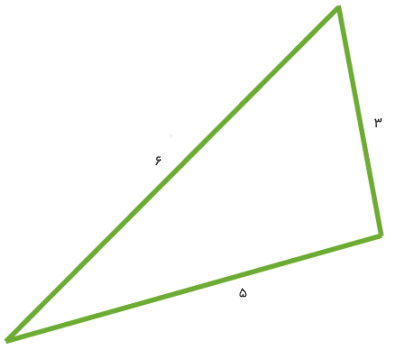
به دلیل مساوی نبودن اندازه ضلعها، مثلث بالا از نوع مختلف الاضلاع است. رابطه تعیین محیط این نوع مثلث به صورت زیر نوشته میشود:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
- ضلع اول: 3
- ضلع دوم: 5
- ضلع سوم: 6
اندازه ضلعها را در رابطه بالا قرار میدهیم:
6 + 5 + 3 = محیط مثلث
14 = محیط مثلث
در نتیجه، محیط مثلث برابر 14 است.
محیط مثلث قائم الزاویه
مثلث قائم الزاویه، مثلثی با یک زاویه راست یا قائمه (90 درجه) است. به ضلعهای تشکیل دهنده زاویه راست، «ساق» و ضلع مقابل زاویه راست، «وتر» میگویند. تصویر زیر، نمونهای از یک مثلث قائم الزاویه را نمایش میدهد. در مثلث قائم الزاویه، معمولا از علامت □ بر روی گوشه دارای زاویه راست استفاده میشود.
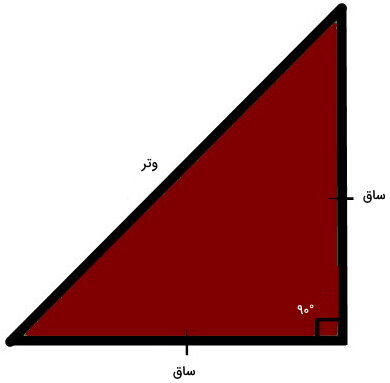
محاسبه محیط مثلث قائم الزاویه، تفاوت چندانی با مثلثهای مختلف الاضلاع ندارد. تفاوت اصلی بین مثلث قائم الزاویه با دیگر مثلثها، امکان استفاده از قضیه فیثاغورس برای تعیین اندازه یک ضلع از روی اندازه دو ضلع دیگر است. به عبارت دیگر، امکان محاسبه محیط مثلثهای قائم، با دانستن اندازه دو ضلع آنها وجود دارد. مثلث قائم الزاویه میتواند متساوی الساقین نیز باشد. در این صورت، از فرمول محیط مثلث متساوی الساقین برای جمع اندازه ضلعهای آن استفاده میشود.
عبارت جبری محیط مثلث قائم الزاویه
در مثلثهای قائم الزاویه، معمولا وتر را با حرف c و ساقها را با حروف a و b نمایش میدهند.
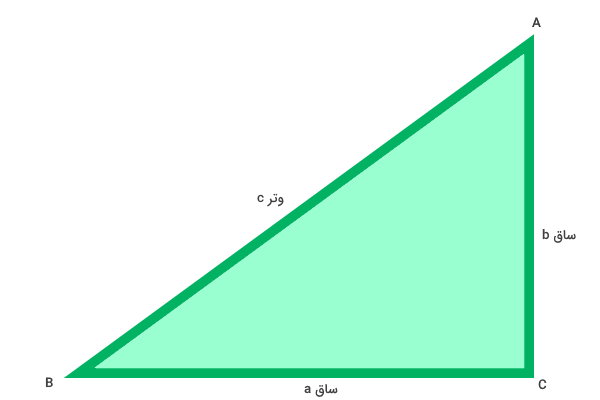
بر اساس قضیه فیثاغورس، رابطه ریاضی بین اندازههای وتر و دو ساق برابر است با:
- c: وتر
- a: یکی از ساقها
- b: ساق دیگر
با استفاده از رابطه بالا میتوان فرمول محیط مثلث قائم الزاویه با دو ساق را به دست آورد:
- P: محیط
- a: اندازه یکی از ساقها
- b: اندازه ساق دیگر
به پیچیدگی محاسبه محیط مثلث قائم الزاویه با دو ضلع نسبت به مثلثهای دیگر، مثالها و مفاهیم مربوط به آن را در مطلب «محیط مثلث قائم الزاویه — به زبان ساده + حل مثال های متنوع» توضیح دادهایم.
مثال های محیط مثلث
در این بخش، چندین مثال متنوع از محیط انواع مثلثها را حل میکنیم.
مثال 5: محاسبه مسافت طی شده
شخصی در یک مدرسه با ساختمان مثلثی شکل تحصیل میکند. او برای اندازهگیری محیط ساختمان مدرسه، در اطراف آن قدم میزند. تصویر زیر، شکل ساختمان و تعداد قدمهای شخص در هر ضلع آن را نمایش میدهد. محیط ساختمان مدرسه را بر حسب قدم تعیین کنید. اگر هر قدم، معادل 0/5 متر (یک دوم متر) باشد، محیط ساختمان چند متر است؟
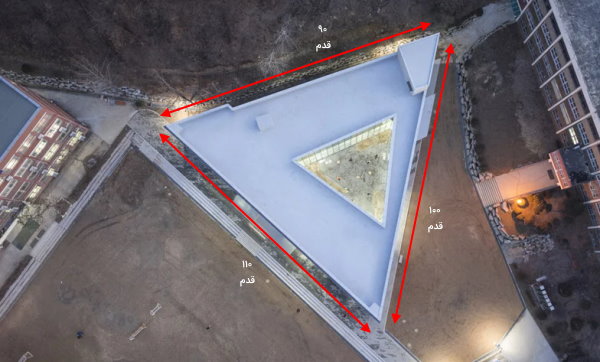
برای اندازهگیری اندازه دور ساختمان بالا، از رابطه محیط مثلث استفاده میکنیم:
ضلع سوم + ضلع دوم + ضلع اول = محیط ساختمان
تعداد قدمها را درون رابطه بالا قرار میدهیم:
110 + 90 + 100 = محیط ساختمان
300 = محیط ساختمان
بنابراین، محیط ساختمان مثلثی برابر 300 قدم است. اگر هر قدم را برابر 0/5 متر یا نصف یک متر در نظر بگیریم، محیط ساختمان برابر خواهد بود با:
0/5 × 300 = محیط ساختمان
یا
2 ÷ 300 = محیط ساختمان
150 = محیط ساختمان
در نتیجه، محیط این ساختمان برابر 150 متر است.
مثال 6: مقایسه محیط مثلثهای متفاوت
محیط مثلثهای زیر را پیدا کنید. با مقایسه محیط این مثلثها، چه نتیجهای میتوان گرفت؟
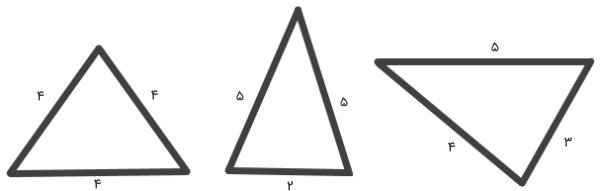
محاسبه محیط مثلثهای بالا را از مثلث الف شروع میکنیم. فرمول محیط را برای این مثلث مینویسیم:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث الف
5 + 4 + 3 = محیط مثلث الف
12 = محیط مثلث الف
محاسبات بالا را برای مثلث ب نیز انجام میدهیم:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث ب
2 + 5 + 5 = محیط مثلث ب
12 = محیط مثلث ب
برای مثلث ج نیز داریم:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث ج
4 + 4 + 4 = محیط مثلث ج
12 = محیط مثلث ج
به این ترتیب، محیط تمام مثلثهای بالا برابر با 12 است. از این مثال میتوانیم نتیجه بگیریم که محیط مثلثهایی با ضلعهای متفاوت و شکلهای متفاوت میتواند با هم برابر باشد.
مثال 7: محاسبه محیط مثلث متساوی الاضلاع
محیط مثلث متساوی الاضلاع زیر چند سانتیمتر است؟
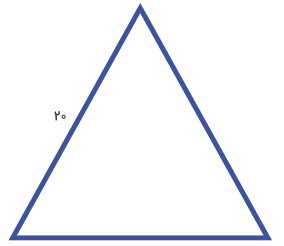
اندازه مثلث متساوی الاضلاع بالا برابر 20 سانتیمتر است. رابطه محیط این مثلث به صورت زیر نوشته میشود:
اندازه یک ضلع × 3 = محیط مثلث متساوی الاضلاع
- P: محیط
- a: اندازه یک ضلع برابر 20 سانتیمتر
اندازه ضلع را درون فرمول بالا قرار میدهیم و آن را حل میکنیم:
در نتیجه، محیط این مثلث متساوی الاضلاع برابر 60 سانتیمتر است.
مثال 8: مقایسه نسبت ضلع به محیط در دو مثلث
دو مثلث مختلف اضلاع را به گونه ای رسم کردهایم که اندازه هر ضلع مثلث بزرگ، دو برابر اندازه ضلع مشابه آن در مثلث کوچک باشد. محیط هر مثلث را حساب کنید. سپس، نسبت اندازه بزرگترین ضلع هر مثلث به اندازه محیط را به دست بیاورید.
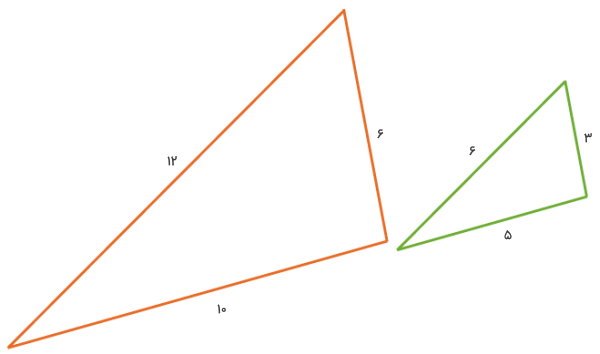
محیط شکل بزرگ توسط رابطه زیر محاسبه میشود:
ضلع سوم + ضلع دوم + ضلع اول = محیط شکل بزرگ
- اندازه ضلع اول برابر 6
- اندازه ضلع دوم برابر 10
- اندازه ضلع سوم برابر 12
12 + 10 + 6 = محیط شکل بزرگ
28 = محیط شکل بزرگ
نسبت بزرگترین ضلع این مثلث به محیط آن برابر است با:
محیط شکل کوچک از رابطه زیر به دست میآید:
ضلع سوم + ضلع دوم + ضلع اول = محیط شکل کوچک
- اندازه ضلع اول برابر 3
- اندازه ضلع دوم برابر 5
- اندازه ضلع سوم برابر 6
6 + 5 + 3 = محیط شکل کوچک
14 = محیط شکل کوچک
نسبت بزرگترین ضلع این مثلث به محیط آن برابر است با:
همان طور که مشاهده میکنید، نسبت بزرگترین ضلع به محیط در هر دو مثلث با هم برابر است. البته به دلیل دو برابر بودن اندازه تمام ضلعهای مثلث بزرگ نسبت به ضلعهای مشابه در مثلث کوچک، نسبت محیط مثلث بزرگ به مثلث کوچک برابر با 2 میشود.
مثال 9: مقایسه محیط شکل های هندسی مختلف
محیط چند ضلعیهای منتظم زیر را حساب کرده و اندازههای به دست آمده را با هم مقایسه کنید. اندازه تمام ضلعهای هر سه چند ضلعی را برابر با 1 در نظر بگیرید.
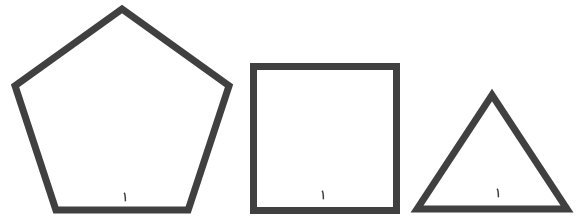
اندازه ضلعهای تمام شکلهای بالا برابر 1 است. به این ترتیب، محیط سه ضلعی به صورت زیر محاسبه میشود:
1 + 1 + 1 = محیط سه ضلعی
3 = محیط سه ضلعی
محیط چهار ضلعی، از رابطه زیر به دست میآید:
1 + 1 + 1 + 1 = محیط چهار ضلعی
4 = محیط چهار ضلعی
محیط پنج ضلعی نیز برابر است با:
1 + 1 + 1 + 1 + 1 = محیط پنج ضلعی
5 = محیط پنج ضلعی
همان طور که مشاهده میکنید، در صورت برابر بودن اندازه ضلعها، با اضافه شدن تعداد ضلعها، محیط افزایش مییابد. به علاوه، محیط شکلهای چند ضلعی منتظم، نسبتی از اندازه یک ضلع آنها است. به عنوان مثال، محیط مربع، 4 برابر اندازه یکی از ضلعهای آن و محیط پنج ضلعی منتظم، 5 برابر اندازه یکی از ضلعهای آن است.
مثال 10: محیط شکل ترکیب شده با مثلث
شکل زیر، ترکیبی از نیمدایره و یک مثلث مختلف الاضلاع است. اگر محیط کمان نیم دایره برابر 15 سانتیمتر باشد، محیط کل شکل چقدر خواهد بود؟
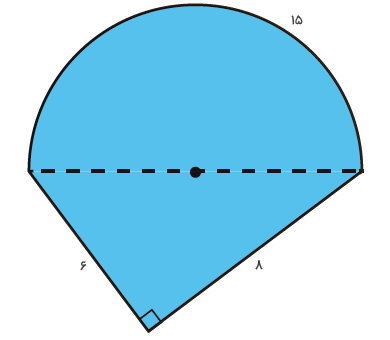
محیط هر شکل، اندازه دور آن شکل است. بنابراین محیط شکل بالا، از جمع محیط کمان نیمدایره با دو ضلع مثلث به دست میآید:
محیط کمان + ضلع دوم مثلث + ضلع اول مثلث = محیط شکل
15 + 8 + 6 = محیط شکل
29 = محیط شکل
در نتیجه، محیط شکل ترکیبی برابر 29 سانتیمتر است.
مثال 11: محاسبه محیط مثلث با ضلع متغیر
اندازه ضلعهای یک مثلث بر اساس متغیر x داده شده است. محیط این مثلث را بر حسب x به دست آورید و آن را ساده کنید. در انتها، محیط را با در نظر گرفتن x=3 به دست بیاورید.
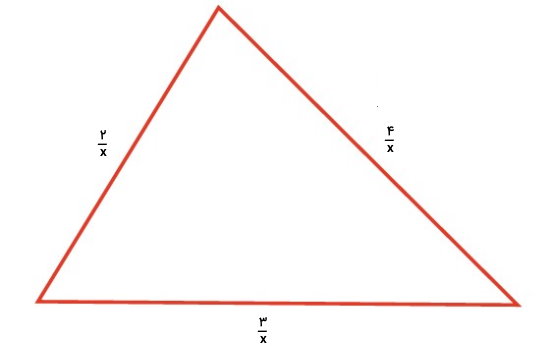
به منظور تعیین محیط شکل بالا، از فرمول زیر استفاده میکنیم:
- P: محیط شکل
- a: اندازه ضلع اول برابر
- b: اندازه ضلع دوم
- c: اندازه ضلع سوم
اندازه ضلع را درون فرمول قرار میدهیم:
محیط شکل برابر عبارت جبری بالا است. به دلیل برابر بودن مخرج تمام کسرها، از آنها، مخرج مشترک میگیریم:
محیط شکل برابر با است. اگر x=3 باشد، محیط برابر خواهد بود با:
مثال 12: محاسبه محیط مثلث قائم الزاویه به کمک قضیه فیثاغورس
در شکل زیر، زاویه بین دو ضلع AB و BC (زاویه راس B) برابر 90 درجه است. محیط این شکل را حساب کنید.
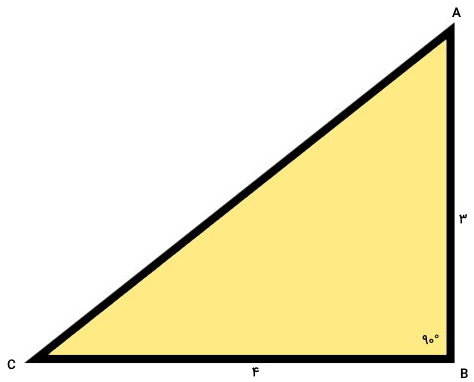
شکل بالا، یک مثلث قائم الزاویه را نمایش میدهد که اندازه دو ساق آن داده شده است. فرمول محیط این شکل به صورت زیر نوشته میشود:
- P: محیط شکل
- a: اندازه ساق اول برابر 3
- b: اندازه ساق دوم برابر 4
- c: اندازه وتر
برای به دست آوردن محیط، به اندازه تمام ضلعها نیاز داریم. مثلثهای قائم الزاویه، از قضیه فیثاغورس پیروی میکنند. بر اساس این قضیه، رابطه زیر بین اندازه وتر و ساقهای یک مثلث قائم الزاویه وجود دارد:
- c: وتر مثلث قائم الزاویه
- a: ساق اول برابر 3
- b: ساق دوم برابر 4
اندازههای معلوم را در رابطه بالا قرار میدهیم و آن را حل میکنیم:
اندازه وتر برابر 5 است. این اندازه را به همراه اندازه ساقها (3 و 4) درون فرمول محیط قرار میدهیم:
در نتیجه محیط این مثلث قائم الزاویه برابر با 12 است.
محاسبه آنلاین محیط مثلث
سایتهای اینترنتی متعددی در زمینه محاسبه آنلاین محیط مثلث وجود دارند. به عنوان مثال، اگر عبارت انگلیسی «triangle perimeter» را در سایت گوگل جستجو کنید، کادر زیر در ابتدای صفحه نتایج ظاهر میشود.
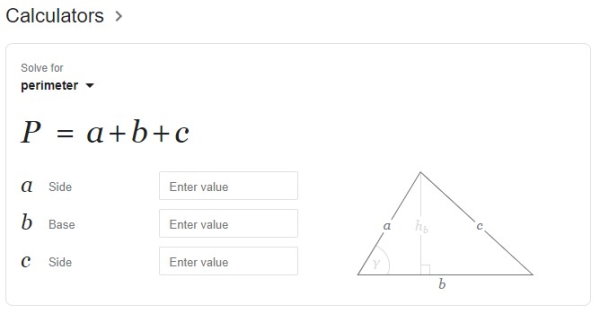
با وارد کردن اندازه ضلعهای مثلث در کادرهای مرتبط، محاسبه محیط انجام میگیرد. به عنوان مثال، تصویر زیر، محیط مثلثی با ضلعها 17، 19 و 25 را نمایش میدهد.
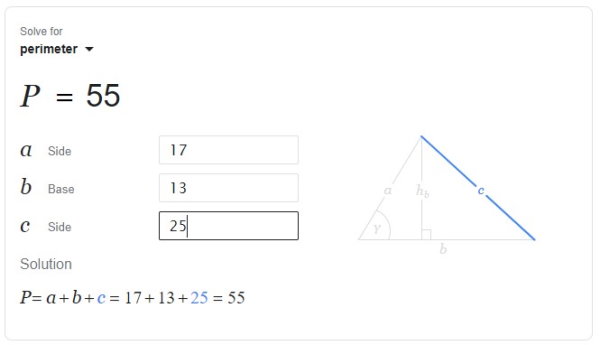
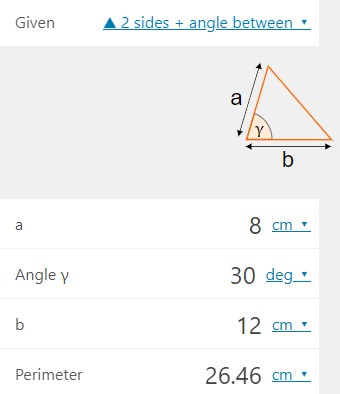
یکی دیگر از ابزارهای کاربردی برای محاسبه آنلاین محیط مثلث، سایت Omnicalculator (+) است. ماشین حساب این سایت، امکان محاسبه محیط با استفاده اندازه دو ضلع و زاویه بین و دو زاویه و ضلع بین را نیز فراهم میکند. به عنوان مثال، تصویر زیر، محاسبه محیط مثلثی با دو ضلع 8 و 12 سانتیمتر و زاویه بین 30 درجه را نمایش میدهد.
آزمون سنجش یادگیری محیط مثلث
در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث محیط مثلث را با طرح سوالهای چندگزینهای میسنجیم. پس از جواب دادن به تمام سوالها، نتیجه آزمون برای شما به نمایش درمیآید.
محیط مثلثی به ضلعهای 3، 3 و 4 واحد طول، چند است؟
12
10
8
7
محیط مثلث، از جمع اندازه تمام ضلعهای آن به دست میآید. بنابراین:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
4 + 3 + 3 = محیط مثلث
10 = محیط مثلث
در نتیجه، محیط مثلث مورد سوال برابر با 10 واحد طول است.
مثلث متساویالاضلاعی به اندازه ضلع 17 متر را در نظر بگیرید. محیط مثلث چیست؟
17 متر
17 متر مربع
51 متر
51 متر مربع
مثلث متساویالاضلاع، مثلثی با ضلعهای برابر است. محیط این مثلث از رابطه زیر به دست میآید:
ضلع + ضلع + ضلع = محیط مثلث متساویالاضلاع
ضلع × 3 = محیط مثلث متساویالاضلاع
17 × 3 = محیط مثلث متساویالاضلاع
51 = محیط مثلث متساویالاضلاع
یکای محیط با یکای ضلعها یکسان در نظر گرفته میشود. بنابراین، محیط مثلث، 51 متر است.
محیط مثلثی برابر با 15 سانتیمتر است. اگر اندازه دو ضلع آن برابر با 4 و 5 سانتیمتر باشد، اندازه ضلع سوم چند خواهد بود؟
6 سانتیمتر
5 سانتیمتر
4 سانتیمتر
3 سانتیمتر
محیط مثلث، از جمع اندازه تمام ضلعهای آن به دست میآید. بنابراین:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
ضلع سوم + 5 + 4 = 15
5 - 4 - 15 = ضلع سوم
9 - 15 = ضلع سوم
6 = ضلع سوم
در نتیجه، ضلع سوم مثلث برابر با 6 سانتیمتر است.
اندازه محیط یک مثلث متساویالاضلاع برابر با 45 سانتیمتر است. کدامیک یک از گزینههای زیر، اندازه ضلع این مثلث را نمایش میدهد؟
22/5 سانتیمتر
25 سانتیمتر
15 سانتیمتر
9 سانتیمتر
اندازه تمام ضلعهای مثلث متساویالاضلاع برابر است. بنابراین، محیط این مثلث از رابطه زیر به دست میآید:
ضلع + ضلع + ضلع = محیط مثلث متساویالاضلاع
ضلع × 3 = محیط مثلث متساویالاضلاع
در این سوال، محیط مثلث متساویالاضلاع برابر با 45 سانتیمتر است. از اینرو، داریم:
ضلع × 3 = 45
3 ÷ 45 = ضلع
15 = ضلع
در نتیجه، اندازه هر یک از ضلعهای مثلث متساویالاضلاع برابر با 15 سانتیمتر است.
محیط مثلث متساویالساقین با ساق 10 سانتیمتر و قاعده 5 سانتیمتر، چند است؟
15 سانتیمتر
20 سانتیمتر
25 سانتیمتر
30 سانتیمتر
در مثلث متساویالساقین، اندازه دو ضلع (اندازه ساقها) با هم برابر است. در این مثلث، ضلع سوم با عنوان قاعده شناخته میشود. بر این اساس، محیط مثلث متساویالساقین با استفاده از رابطه زیر به دست میآید:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث متساویالساقین
قاعده + ساق + ساق = محیط مثلث متساویالساقین
قاعده + (ساق × 2) = محیط مثلث متساویالساقین
با توجه به صورت سوال، مقادیر معلوم را درون رابطه بالا قرار میدهیم:
5 + (10 × 2) = محیط مثلث متساویالساقین
5 + 20 = محیط مثلث متساویالساقین
25 = محیط مثلث متساویالساقین
در نتیجه، محیط مثلث متساویالساقین برابر با 25 سانتیمتر است.
اندازه قاعده یک مثلث متساویالساقین برابر با 7 متر است. اگر محیط این مثلث، برابر با 13 سانتیمتر باشد، اندازه هر یک از ساقهای آن چقدر خواهد بود؟
20 متر
33 متر
3 متر
27 متر
محیط مثلث متساویالساقین، با استفاده از رابطه زیر محاسبه میشود:
قاعده + (ساق × 2) = محیط مثلث متساویالساقین
بر اساس صورت سوال، اندازه قاعده برابر با 7 متر و اندازه محیط برابر با 13 متر است. این مقادیر را درون رابطه بالا قرار میدهیم:
7 + (ساق × 2) = 13
7 - 13 = (ساق × 2)
6 = (ساق × 2)
2 ÷ 6 = ساق
3 = ساق
در نتیجه، اندازه هر یک از ساقهای مثلث برابر با 3 متر است.
محیط یک مثلث قائمالزاویه به ساقهای 3 و 4 چند است؟
برای به دست آوردن محیط مثلث، به اندازه هر سه ضلع نیاز داریم. بر اساس صورت سوال، اندازه ساقها (دو ضلع) را داریم. اندازه وتر (ضلع سوم) را با استفاده از قضیه فیثاغورس در مثلثهای قائمالزاویه تعیین میکنیم. این قضیه به صورت زیر نوشته میشود:
- c: وتر مثلث قائمالزاویه
- a: یکی از ساقهای مثلث قائمالزاویه برابر با 3
- b: ساق دیگر مثلث قائمالزاویه برابر با 4
اندازههای معلوم را درون رابطه بالا قرار میدهیم:
به این ترتیب، اندازه وتر یا ضلع سوم مثلث را به دست آوردیم. اکنون، این اندازه را به همراه اندازه ساقها درون رابطه محیط مثلث قرار میهیم:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
وتر + ساق دوم + ساق اول = محیط مثلث متساویالساقین
5 + 4 + 3 = محیط مثلث متساویالساقین
12 = محیط مثلث متساویالساقین
در نتیجه، محیط مثلث برابر با 12 است.
محیط یک مثلث قائمه متساویالساقین به وتر سانتیمتر چند است؟
برای به دست آوردن محیط مثلث، به اندازه هر سه ضلع آن نیاز داریم:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
در صورت سوال، اندازه وتر مثلث قائمالزاویه متساویالساقین داده شده است. به دلیل متساویالساقین بودن مثلث، رابطه محیط آن به صورت زیر نوشته میشود:
قاعده + (ساق × 2) = محیط مثلث متساویالساقین
به دلیل قائمه بودن مثلث، میتوان به جای عبارت «قاعده»، از عبارت «وتر» در رابطه بالا استفاده کرد:
وتر + (ساق × 2) = محیط مثلث قائمالزاویه متساویالساقین
اندازه وتر برابر با سانتیمتر است. اندازه ساق، با استفاده از قضیه فیثاغورس در مثلثهای قائمه محاسبه میشود. بر اساس این قضیه، رابطه بین وتر و ساقها عبارت است از:
- c: وتر مثلث قائمالزاویه
- a: یکی از ساقهای مثلث قائمالزاویه
- b: ساق دیگر مثلث قائمالزاویه
در مثلثهای قائمالزاویه متساویالساقین، قضیه فیثاغورس به صورت زیر نوشته میشود:
اندازه وتر را درون این رابطه قرار میدهیم:
بنابراین، اندازه ساقهای مثلث برابر با 4 سانتیمتر است. این مقدار را به همراه اندازه وتر درون رابطه محیط قرار میدهیم:
وتر + (ساق × 2) = محیط مثلث قائمالزاویه متساویالساقین
2√4 + (4 × 2) = محیط مثلث قائمالزاویه متساویالساقین
2√4 + 8 = محیط مثلث قائمالزاویه متساویالساقین
در نتیجه، محیط مثلث برابر با سانتیمتر است.
سوالات متداول در رابطه با محیط مثلث
در این بخش، به برخی از سوالات متداول در رابطه با محیط مثلثها و نحوه اندازهگیری آن پاسخ میدهیم.
تعریف محیط مثلث چیست ؟
محیط مثلث، اندازه دور مثلث است.
محیط مثلث چگونه محاسبه می شود ؟
محیط مثلث، با جمع اندازه سه ضلع آن محاسبه میشود.
فرمول محیط مثلث چیست ؟
فرمول محیط مثلث، P=a+b+c است. در این فرمول، P، محیط و سه حرف بعدی، اندازه ضلعهای مثلث را نمایش میدهند.
محیط مثلث متساوی الاضلاع چند برابر اندازه یک ضلع آن است؟
محیط مثلث متساوی الاضلاع، سه برابر اندازه یک ضلع آن است.
در کدام مثلث، اندازه ضلع با اندازه محیط متناسب است؟
در مثلث متساوی الاضلاع، اندازه ضلع با اندازه محیط متناسب است.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان(همین مطلب)
- چگونه مساحت مثلث را حساب کنیم؟ + فیلم آموزشی و تمرین با جواب
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال
- فرمول هرون — به زبان ساده
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه — به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع













فیلمه خوب بود.
عالی بود من کلاس هفتمم خیلی چیزا یاد گرفتم بازم از این مطالب مفید بزارید
بد نبود
بدک نبود