مساحت مستطیل به صورت جبری – فرمول های ریاضی + حل مثال

فرمول «S=a×b»، مساحت مستطیل به صورت جبری است. عبارت‌های جبری، متغیرها و عملگرهایی هستند که برای نمایش ریاضی روابط مورد استفاده قرار می‌گیرند. به عنوان مثال، مساحت مستطیل به صورت «طول ضربدر عرض» بیان می‌شود. با این وجود، نحوه بیان مساحت مستطیل در زبان ریاضی می‌تواند به صورت «A=l×w» باشد. در این آموزش، فرمول‌های مساحت مستطیل به صورت جبری و روش‌های محاسبه مساحت مستطیل با ضلع و قطر را به همراه حل چند مثال توضیح می‌دهیم.

مساحت مستطیل چیست؟

مساحت مستطیل، اندازه سطحی است که این شکل هندسی پوشش می‌دهد. به عنوان مثال، یک شی مستطیلی شکل مانند کتاب یا دفتر را در نظر بگیرید.

اگر این شی را بر روی میز یا زمین قرار دهیم، سطح زمین به اندازه مساحت آن شی پوشیده می‌شود.

مساحت مستطیل چگونه بدست می‌آید؟

با ضرب طول (ضلع بزرگ) مستطیل در عرض (ضلع کوچک) آن، مساحت مستطیل به دست می‌آید. فرمول مساحت مستطیل به زبان فارسی عبارت است از:

 عرض × طول = مساحت مستطیل

فیلم آموزش محاسبه مساحت مستطیل (رایگان) در فرادرس

کلیک کنید

به عنوان مثال، اگر طول و عرض یک مستطیل به ترتیب برابر با 9 و 5 باشد، مساحت آن به صورت زیر محاسبه می‌شود:

5 × 9 = مساحت مستطیل

45 = مساحت مستطیل

مساحت مستطیل به صورت جبری چگونه است؟

مستطیل زیر را در نظر بگیرید. طول‌های این مستطیل را با حرف l و عرض‌های آن را با حرف w مشخص کرده‌ایم. در فرمول‌های ریاضی، مساحت مستطیل با حرف A نمایش داده می‌شود.

اکنون، فرمول مساحت مستطیل را با استفاده از حروف می‌نویسیم:

$$A = l \times w$$

فرمول بالا، مساحت مستطیل به صورت جبری است. عبارت‌های جبری، به منظور نمایش روابط ریاضی با حروف، اعداد و علامت‌ها مورد استفاده قرار می‌گیرند. در برخی از منابع آموزشی، مانند کتاب‌های درسی پایه متوسطه، مساحت مستطیل با عبارت جبری به صورت زیر نوشته شده است:

$$S = a \times b$$

• S: مساحت مستطیل
• a: یکی از ضلع‌های مستطیل
• b: ضلع دیگر مستطیل

در این آموزش، از فرمول جبری بالا برای محاسبه مساحت مستطیل استفاده می‌کنیم.

مثال 1: محاسبه مساحت مستطیل به صورت جبری

اندازه سطح یک میز مستطیلی به طول 70 سانتی‌متر و عرض 30 سانتی‌متر را به دست بیاورید.

برای محاسبه اندازه سطح میز، فرمول ریاضی مساحت مستطیل را می‌نویسیم:

$$S = a \times b$$

• S: مساحت میز
• a: طول میز برابر 70 سانتی‌متر
• b: عرض میز برابر 30 سانتی‌متر

اندازه طول و عرض میز را درون فرمول قرار می‌دهیم و آن را حل می‌کنیم:

$$S = ۷۰ \times ۳۰$$

$$S = ۲۱۰۰$$

در نتیجه، مساحت مستطیل برابر 2100 سانتی‌متر مربع است.

مثال 2: محاسبه طول مستطیل با مساحت

اندازه سطح یک موکت برابر 12 متر مربع و عرض آن برابر 3 متر است. طول موکت را حساب کنید.

سطح موکت بالا، به شکل مستطیل است. از این‌رو، به منظور تعیین طول موکت می‌توانیم از فرمول مساحت مستطیل به صورت جبری استفاده کنیم:

$$S = a \times b$$

• S: مساحت موکت برابر 12 متر مربع
• a: طول موکت
• b: عرض موکت برابر 3 متر

$$۱۲ = a \times ۳$$

در رابطه بالا، به دنبال تعیین طول موکت (l) هستیم. به همین دلیل، باید رابطه را بر حسب l بنویسیم:

$$l = \frac {۱۲} {۳}$$

$$l = ۴$$

در نتیجه، طول موکت برابر با 4 متر است.

مثال 3: تعیین عبارت جبری مساحت مستطیل

اندازه‌های طول و عرض مستطیل زیر به صورت جبری بیان شده‌اند. یک عبارت جبری برای پیدا کردن مساحت آن بنویسید. اگر x برابر 3 باشد، مقدار عددی مساحت مستطیل چقدر است؟

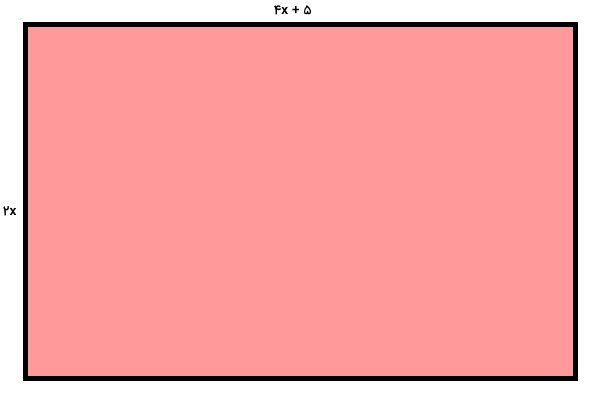
روند حل این مثال، تفاوت چندانی با مثال‌های قبل ندارد. در اینجا نیز از فرمول مساحت مستطیل استفاده می‌کنیم و به جای عدد، عبارت‌های جبری طول و عرض را قرار می‌دهیم:

$$S = a \times b$$

• S: مساحت مستطیل
• a: طول مستطیل برابر ۴x+۵
• b: عرض مستطیل برابر ۲x

$$S = (۴x + ۵) \times (۲x)$$

به این ترتیب، عبارت جبری محیط مستطیل به دست می‌آید. البته می‌توانیم رابطه بالا را با انجام ضرب متغیرها ساده‌تر کنیم:

$$S = (۴x \times + ۲x) + (۵ \times ۲x)$$

$$S = ۸x^۲ + ۱۰x$$

با قرار دادن عدد مورد نظر به جای x، امکان تعیین مقدار عددی مساحت نیز فراهم می‌شود. در این مثال، عدد سه را جایگزین متغیر x می‌کنیم:

$$S = ۸(۳)^۲ + ۱۰(۳)$$

$$S = ۸(۹) + ۱۰(۳)$$

$$S = ۷۲ + ۳۰$$

$$S = ۱۰۲$$

در نتیجه، مساحت مستطیل برابر 102 است.

مساحت مستطیل به صورت جبری با قطر

قطر مستطیل، آن را به دو مثلث قائم الزاویه تقسیم می‌کند. طول و عرض مستطیل، ساق‌های این دو مثلث هستند.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

قطر نیز به عنوان وتر این مثلث‌ها در نظر گرفته می‌شود.

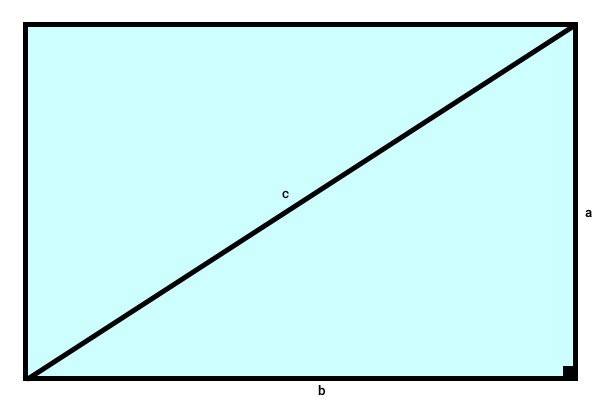
محاسبه اندازه وتر مثلث قائم الزاویه، با استفاده از رابطه زیر (قضیه فیثاغورس) انجام می‌گیرد:

$$c^۲ = a^۲ + b^۲$$

• c: وتر
• a: ساق اول
• b: ساق دوم

بر اساس این رابطه، اندازه هر یک از ساق‌های مثلث (ضلع‌های مستطیل) برابر است با:

$$a = \sqrt { c^۲ - b^۲ }$$

$$b = \sqrt { c^۲ - a^۲ }$$

به عبارت دیگر، با مشخص بودن اندازه قطر و یکی از ضلع‌های مستطیل، امکان محاسبه اندازه ضلع سوم نیز فراهم می‌شود. اگر روابط بالا را در فرمول مساحت مستطیل به صورت جبری قرار دهیم، به فرمول‌های زیر می‌رسیم:

$$S = a \times \sqrt { c^۲ - a^۲ }$$

$$S = b \times \sqrt { c^۲ - b^۲ }$$

مثال 4: محاسبه مساحت مستطیل از روی قطر

مساحت یک مستطیل با قطر 25 سانتی‌متر و عرض 7 سانتی‌متر را حساب کنید.

با توجه به اطلاعات مسئله، فرمول مساحت مستطیل با قطر را می‌نویسیم:

$$S = a \times \sqrt { c^۲ - a^۲ }$$

• S: مساحت مستطیل
• a: عرض مستطیل برابر 7 سانتی‌متر
• c: قطر مستطیل برابر 25 سانتی‌متر

$$S = ۷ \times \sqrt { ۲۵^۲ - ۷^۲ }$$

$$S = ۷ \times \sqrt { ۶۲۵ - ۴۹ }$$

$$S = ۷ \times \sqrt { ۵۷۶ }$$

$$S = ۷ \times ۲۴$$

$$S = ۱۶۸$$

در نتیجه، مساحت مستطیل برابر 168 سانتی‌متر مربع است.

فرمول مساحت مستطیل، بخشی از فرمول محاسبه حجم مکعب مستطیل است. در صورت تمایل به آشنایی با این فرمول، مطالعه مطلب «حجم مکعب مستطیل چیست؟ — به زبان ساده + حل تمرین و مثال‌های متنوع» را به شما پیشنهاد می‌کنیم.

سوالات متداول در رابطه با مساحت مستطیل به صورت جبری

در این بخش، به برخی از سوالات پرتکرار در رابطه با مساحت مستطیل و عبارت‌های جبری مورد استفاده برای محاسبه آن می‌پردازیم.

فیلم مجموعه آموزش دروس متوسطه دوم و کنکور – درس، تمرین، حل مثال و تست در فرادرس

کلیک کنید

تعریف مساحت مستطیل چیست؟

به اندازه سطح درون ضلع‌های مستطیل، مساحت مستطیل می‌گویند.

محاسبه مساحت مستطیل چگونه است؟

مساحت مستطیل با ضرب طول در عرض آن محاسبه می‌شود.

فرمول مساحت مستطیل با عبارت جبری چگونه نوشته می شود؟

فرمول S=a×b، رابطه مساحت مستطیل با صورت جبری است.