مساحت متوازی الاضلاع چیست؟ — فیلم آموزش رایگان + حل تمرین و مثال
مساحت متوازی الاضلاع برابر «قاعده ضربدر ارتفاع» است. البته امکان محاسبه این مساحت با استفاده از اندازه قطرها و اندازه ضلعها نیز وجود دارد. علاوه بر این میتوان مساحت متوازیالاضلاع را به صورت برداری هم تعیین کرد. در این آموزش، به معرفی انواع فرمولها و روشهای محاسبه مساحت متوازی الاضلاع به همراه حل چندین مثال میپردازیم. سپس، برخی از این فرمولها را به صورت تصویری اثبات میکنیم.
فیلم آموزشی مساحت متوازی الاضلاع
متوازی الاضلاع چیست؟
به هر چهارضلعی که ضلعهای روبهرویی آن با هم موازی و مساوی باشند، متوازی الاضلاع میگویند.
شکلهای مربع، مستطیل و لوزی، سه متوازی الاضلاع با ویژگیهای خاص هستند.
مساحت متوازی الاضلاع چیست؟
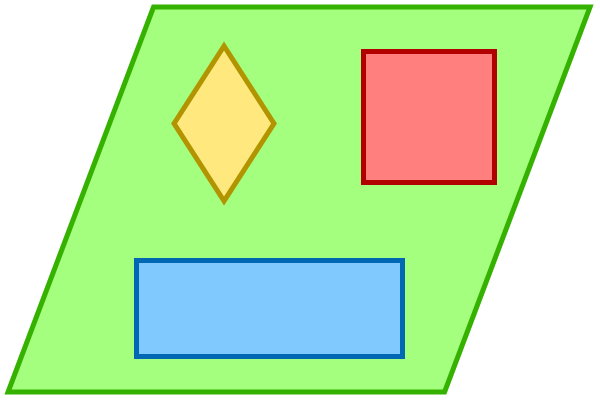
مساحت متوازی الاضلاع، اندازه سطح آن است. به عنوان مثال، تمام شکلهای زیر، متوازی الاضلاع هستند.
محدودهای که درون ضلعهای این شکلها قرار میگیرد، با عنوان مساحت شناخته میشود.

برای درک بهتر مفهوم مساحت متوازی الاضلاع، شکلی مشابه تصویر زیر را رسم کنید.
سپس، یک مداد یا قلم بردارید و سطح داخل شکل را رنگ بزنید.
رنگ کردن داخل شکل را ادامه دهید تا سطح آن به طور کامل پر شود.

اندازه ناحیه رنگشده، همان مساحت متوازی الاضلاع است. برای محاسبه این اندازه، از اجزای اصلی متوازی الاضلاع نظیر قاعده و ارتفاع استفاده میکنیم.
اجزای متوازی الاضلاع چه هستند؟
از اجزای مهم متوازی الاضلاع میتوان به ضلع، راس (گوشه)، زاویه داخلی، زاویه خارجی، قطر و ارتفاع اشاره کرد.
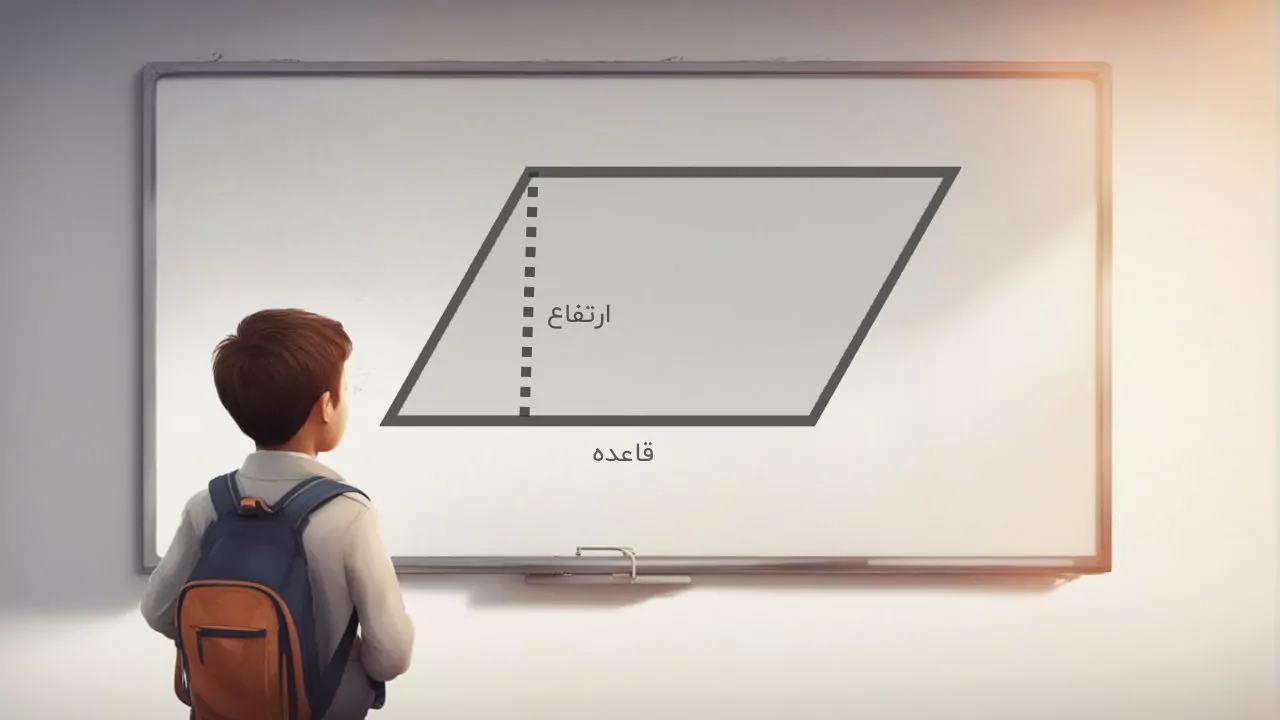
تصویر زیر، دو اندازه اصلی مورد استفاده برای محاسبه مساحت متوازی الاضلاع را نمایش میدهد.
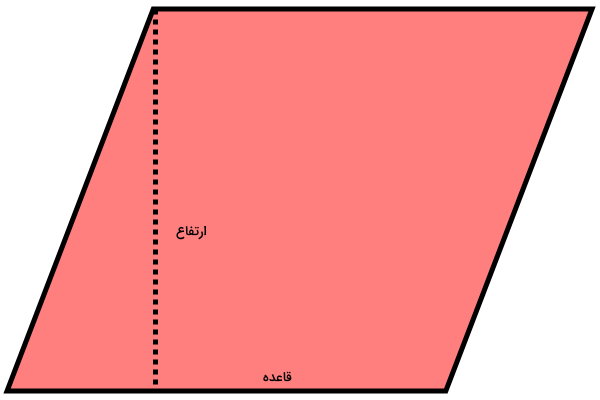
اجزای بالا عبارت هستند از:
- قاعده: معمولا ضلع پایینی متوازی الاضلاع به عنوان قاعده آن در نظر گرفته میشود.
- ارتفاع: فاصله عمودی بین دو ضلع روبهرویی متوازی الاضلاع، ارتفاع است.
توجه داشته باشید که تمام ضلعهای متوازی الاضلاع را میتوان به عنوان قاعده در نظر گرفت. طبق یک تعریف کلی، به ضلعی که ارتفاع بر آن عمود شده باشد، قاعده میگویند. در نتیجه، متوازی الاضلاع، دو قاعده و دو ارتفاع دارد.
مساحت متوازی الاضلاع چگونه بدست می آید ؟
مساحت متوازی الاضلاع از ضرب قاعده در ارتفاع به دست میآید. رابطه کلامی مساحت متوازی الاضلاع به صورت زیر نوشته میشود:
قاعده × ارتفاع = مساحت متوازی الاضلاع
رابطه بالا، شباهت زیادی به رابطه مساحت مثلث دارد. در واقع، محاسبه مساحت مثلث، بر مبنای اصول محاسبه مساحت متوازیالاضلاع صورت میگیرد.
رابطه بین مساحت متوازی الاضلاع و مستطیل
ارتفاع متوازی الاضلاع، این شکل را به یک ذوزنقه و یک مثلث قائم الزاویه تقسیم میکند.
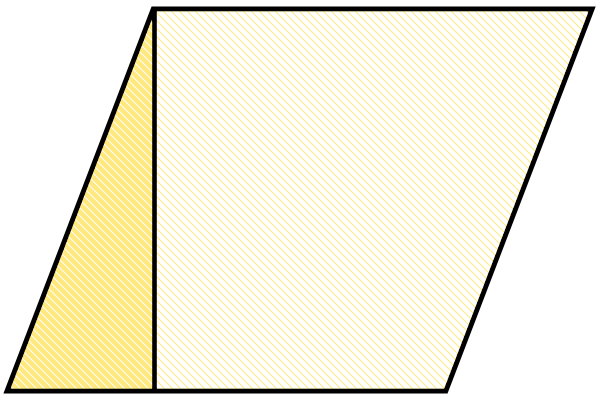
اگر مثلث قائم الزاویه بالا را جدا کنیم و آن را به سمت راست متوازی الاضلاع انتقال دهیم، یک مستطیل به وجود میآید.

مساحت مستطیل بالا، توسط رابطه زیر محاسبه میشود:
عرض × طول = مساحت مستطیل
مساحت این مستطیل برابر با مساحت متوازی الاضلاع، عرض آن برابر با ارتفاع متوازی الاضلاع و طول آن برابر با قاعده متوازی الاضلاع است. در نتیجه، فرمول مساحت متوازیالاضلاع را میتوانیم به صورت زیر بنویسیم:
قاعده × ارتفاع = مساحت متوازی الاضلاع
مثال 1: محاسبه مساحت متوازی الاضلاع با ارتفاع و قاعده
ارتفاع یک متوازی الاضلاع برابر 56 سانتیمتر و قاعده آن برابر 100 سانتیمتر است. مساحت متوازی الاضلاع را به دست بیاورید.
برای حل این مثال، ابتدا رابطه مساحت را مینویسیم و اندازههای معلوم را درون آن قرار میدهیم:
قاعده × ارتفاع = مساحت متوازیالاضلاع
100 × 56 =
5600 =
در نتیجه مساحت متوازیالاضلاه برابر 5600 سانتیمتر مربع است.
مثال 2: محاسبه ارتفاع متوازی الاضلاع از روی مساحت و قاعده
اگر در مثال 1، اندازه قاعده دیگر متوازی الاضلاع برابر با 70 سانتیمتر باشد، اندازه ارتفاع دیگر (ارتفاع نظیر قاعده) آن چقدر خواهد بود.
در مثال 1، مساحت متوازیالاضلاع را برابر با 5600 سانتیمتر مربع به دست آوردیم. به منظور تعیین ارتفاع نظیر قاعده 70 سانتیمتری، اندازه مساحت و قاعده را درون رابطه زیر قرار میدهیم:
قاعده × ارتفاع = مساحت متوازیالاضلاع
70 × ارتفاع = 5600
اکنون، رابطه بالا را بر حسب ارتفاع بازنویسی میکنیم. برای این کار، ارتفاع را در یک سمت رابطه نگه میداریم و عدد 70 را به سمت دیگر رابطه میبریم. به این ترتیب، علامت ضربدر 70 به تقسیم بر 70 تبدیل میشود:
70 ÷ 5600 = ارتفاع
80 = ارتفاع
در نتیجه، ارتفاع متوازی الاضلاع برابر 80 سانتیمتر است.
فرمول مساحت متوازی الاضلاع به صورت جبری چیست؟
در کتابهای ریاضی، مساحت شکلهای هندسی مختلف با استفاده از عبارتهای جبری نمایش داده میشود. عبارتهای جبری، ترکیبی از اعداد، علامتها و حروف معرف رابطههای ریاضی هستند.
در بخش قبلی دیدیم که مساحت متوازی الاضلاع به زبان فارسی برابر است با:
قاعده × ارتفاع = مساحت متوازیالاضلاع
در ریاضیات، مساحت شکلها را با حرف A (ابتدای کلمه Area) یا حرف S (ابتدای کلمه Surface) نمایش میدهند. حروف b و h نیز به ترتیب معرف قاعده و ارتفاع متوازی الاضلاع هستند. بر این اساس، فرمول جبری مساحت متوازیالاضلاع به صورت زیر نوشته میشود:
- S: مساحت
- b: قاعده
- h: ارتفاع
مثال 3: محاسبه مساحت متوازی الاضلاع به صورت جبری
مساحت شکل زیر را از دو طریق حساب کنید.
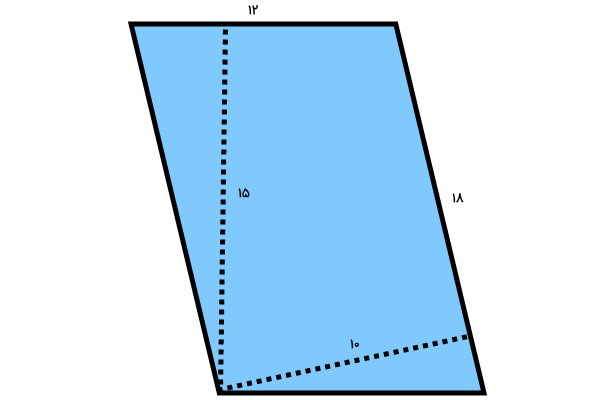
در تصویر بالا، اندازه دو ضلع (قاعده) و دو ارتفاع متوازی الاضلاع داده شده است. برای محاسبه مساحت متوازیالاضلاع میتوانیم از فرمول زیر استفاده کنیم:
- S: مساحت
- b: قاعده
- h: ارتفاع نظیر
نکته مهم در این مثال، استفاده از قاعده و ارتفاع مناسب در فرمول بالا است. قاعده و ارتفاع مورد استفاده باید نظیر یکدیگر باشند. در تصویر بالا، عدد ۱۵، ارتفاع نظیر قاعده ۱۲ است. عدد ۱۰ نیز، ارتفاع نظیر قاعده 1۸ محسوب میشود. در نتیجه، این اعداد باید با هم در فرمول مساحت قرار گیرند. به این ترتیب، در حالت اول داریم:
برای حالت دوم نیز داریم:
در هر حالت، اندازه مساحت متوازیالاضلاع برابر با ۱۸۰ خواهد بود.
مساحت متوازی الاضلاع با مثلثات
یکی دیگر از روشهای محاسبه مساحت متوازی الاضلاع، استفاده از اندازه دو ضلع مجاور و زاویه بین آنها است.
متوازی الاضلاع زیر را در نظر بگیرید.
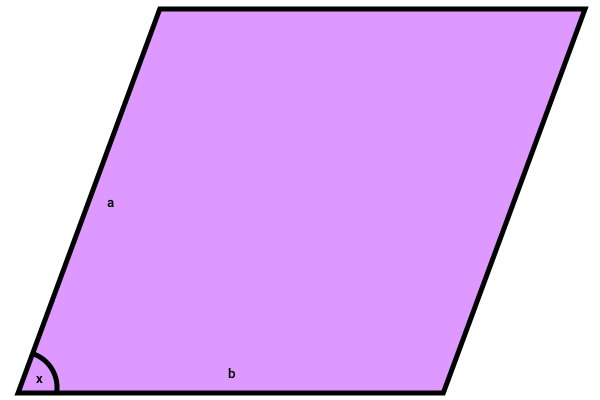
با توجه به شکل بالا، فرمول مساحت متوازیالاضلاع با سینوس به صورت زیر نوشته میشود:
مثال 4: محاسبه مساحت متوازی الاضلاع با داشتن دو ضلع
اندازه ضلعهای یک متوازیالاضلاع برابر و 15 متر است. اگر زاویه بین این دو ضلع برابر 45 درجه باشد، مساحت چقدر است؟
به منظور حل این مثال، از فرمول مساحت متوازی الاضلاع با سینوس استفاده میکنیم:
- S: مساحت
- a: اندازه یکی از ضلعها برابر متر
- b: اندازه ضلع مجاور a برابر 15 متر
- x: زاویه بین a و b برابر 45 درجه
سینوس زاویه 45 درجه برابر رادیکال دو دوم است:
در نتیجه، مساحت متوازیالاضلاع برابر 150 متر مربع است.
مساحت متوازی الاضلاع با قطر
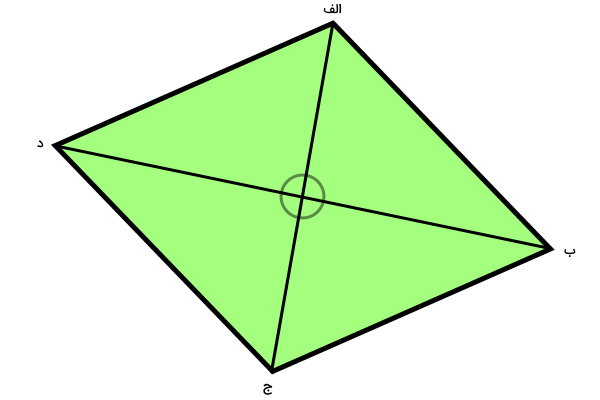
متوازی الاضلاع (الف ب ج د) را در نظر بگیرید. از یکی از گوشههای این متوازی الاضلاع (مانند ج)، پارهخطی را به سمت گوشه مقابل آن (مانند الف) رسم میکنیم.
پارهخط (ج الف)، قطر متوازیالاضلاع است.
متوازیالاضلاع، دو قطر دارد که از وسط یکدیگر عبور میکنند. به منظور محاسبه مساحت متوازی الاضلاع با قطر، به اندازه هر دو قطر و یکی از زاویههای بین آنها نیاز داریم.
فرمول مساحت متوازیالاضلاع با قطر به صورت زیر نوشته میشود:
- S: مساحت
- d1: یکی از قطرها
- d2: قطر دیگر
- y: یکی از زاویههای بین دو قطر
مثال 5: محاسبه مساحت متوازیالاضلاع بر حسب قطر
اندازه قطرهای متوازی الاضلاع زیر برابر 13 و 10 است. مساحت آن را به دست بیاورید.
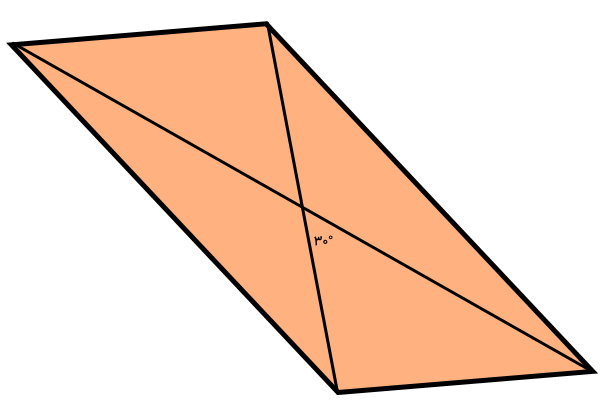
در شکل بالا، یکی از زاویههای بین دو قطر متوازیالاضلاع داده شده است. این زاویه و اندازه قطرها را درون فرمول مخصوص محاسبه مساحت متوازیالاضلاع بر حسب قطر قرار میدهیم:
- S: مساحت
- d1: یکی از قطرها برابر 13
- d2: قطر دیگر برابر 10
- y: یکی از زاویههای بین دو قطر برابر 30 درجه
سینوس زاویه 30 درجه برابر یکدوم یا 0/5 است:
در نتیجه، مساحت متوازیالاضلاع برابر 32/5 است. فرمولی که در این مثال استفاده کردیم، فرم اسکالر یا عددی مساحت متوازیالاضلاع با قطر بود. امکان نوشتن این فرمول به صورت برداری نیز وجود دارد که در بخش بعدی به معرفی و اثبات آن خواهیم پرداخت.
در صورت تمایل به مشاهده مثالهای بیشتر راجع به مساحت متوازیالاضلاع، مطالعه مطلب «نمونه سوال مساحت متوازیالاضلاع با جواب — حل تمرینهای متنوع» را به شما پیشنهاد میکنیم.
مساحت متوازی الاضلاع با ضرب خارجی
در بخشهای قبلی، با فرمولهای محاسبه مساحت متوازیالاضلاع بر حسب ضلع و قطر آشنا شدیم. اگر ضلعها و قطرهای متوازی الاضلاع را به صورت برداری بنویسیم، امکان تعیین مساحت با ضرب خارجی بردارها فراهم میشود.
مساحت متوازیالاضلاع با ضرب خارجی ضلعها
برای محاسبه برداری مساحت این متوازیالاضلاع، به مختصات گوشههای آن نیاز داریم. با استفاده از مختصات گوشهها و جمع برداری، بردار هر یک از ضلعها به دست میآید:
فرمول مساحت متوازیالاضلاع با ضرب خارجی ضلعها به صورت زیر نوشته میشود:
حاصل ضرب خارجی بالا، در واقع حاصل دترمینان ضلعهای متوازیالاضلاع است:
ابن فرمول شباهت زیادی به فرمول مساحت متوازیالاضلاع با ضرب اسکالر ضلعها در سینوس زاویه بین آنها دارد. با این تفاوت که به دلیل برداری بودن محاسبات، در اینجا نیازی به دانستن زاویه نیست.
مساحت متوازیالاضلاع با ضرب خارجی قطرها
فرمول برداری مساحت متوازیالاضلاع با قطر عبارت است از:
این فرمول، بر اساس فرمول مساحت با ضلعها به دست میآید. در بخش بعدی، نحوه اثبات فرمول بالا را توضیح میدهیم.
اثبات فرمول مساحت متوازیالاضلاع با ضرب خارجی قطرها
به منظور اثبات فرمول مساحت متوازیالاضلاع با ضرب خارجی قطرها، شکل زیر را در نظر بگیرید. این شکل، ضلعها و قطرهای متوازیالاضلاع را به صورت برداری نمایش میدهد.
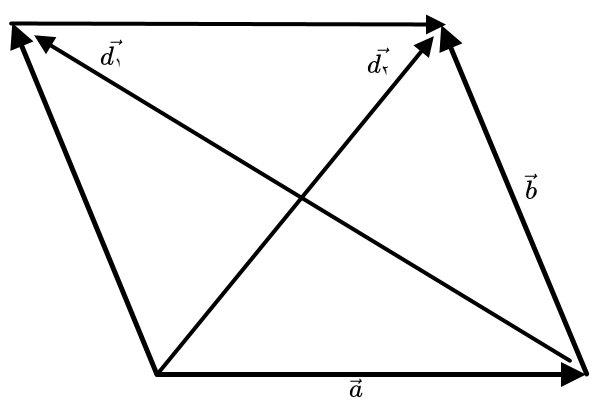
فرمول برداری مساحت متوازیالاضلاع برابر است با:
بر اساس تصویر بالا میتوانیم رابطه بین ضلعهای متوازیالاضلاع با قطر آن را به صورت جمع و تفریق برداری بنویسیم:
اگر دو طرف عبارتهای بالا را در هم ضرب کنیم، خواهیم داشت:
ضرب خارجی هر بردار در خودش برابر صفر است. بنابراین:
در ضرب خارجی، اگر جای بردارها عوض شود، علامت آنها تغییر میکند:
ضرب خارجی بردار a در b، مساحت متوازیالاضلاع است. رابطه بالا را بر حسب این ضرب مینویسیم:
در نتیجه، فرمول مساحت متوازیالاضلاع با استفاده از ضرب خارجی بردارهای قطر به دست میآید:
اثبات مساحت ذوزنقه از روی مساحت متوازی الاضلاع
اگر دو ذوزنقه همشکل و هماندازه را کنار هم قرار دهیم، یک متوازی الاضلاع حاصل می شود که قاعده آن برابر مجموع قاعدههای ذوزنقه و ارتفاع آن برابر ارتفاع ذوزنقه است. پس مساحت ذوزنقه نصف مساحت این متوازی الاضلاع است.
به عنوان مثال، دو ذوزنقه همنهشت زیر را در نظر بگیرید. اندازههای متناظر در این دو ذوزنقه، مساوی هستند.

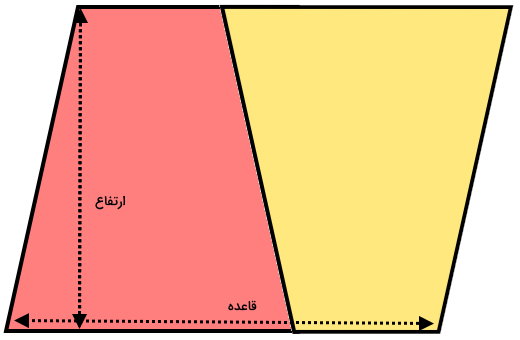
اگر یکی از ذوزنقههای بالا را دَوَران دهیم و یکی از ضلعهای متناظر آنها را بر روی یکدیگر منطبق کنیم، متوازیالاضلاع زیر تشکیل میشود.
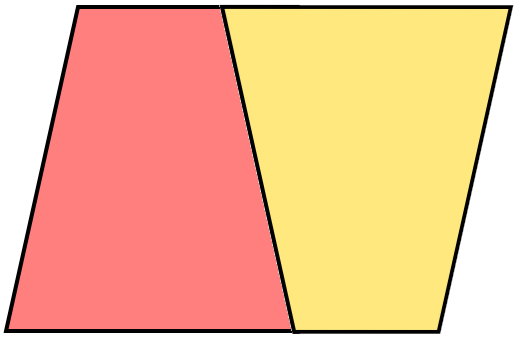
مساحت متوازیالاضلاع بالا از جمع مساحت دو ذوزنقه به دست میآید:
ذوزنقه زرد + ذوزنقه قرمز = مساحت متوازیالاضلاع
به دلیل برابر بودن ذوزنقه، رابطه مساحت از روی شکل برابر است با:
(مساحت یک ذوزنقه) × 2 = مساحت متوازیالاضلاع
رابطه کلی مساحت متوازیالاضلاع نیز به صورت زیر نوشته میشود:
ارتفاع × قاعده = مساحت متوازیالاضلاع
ارتفاع متوازیالاضلاع، با ارتفاع ذوزنقهها یکسان است. با این وجود، قاعده متوازیالاضلاع، از جمع دو قاعده ذوزنقه به دست میآید. به عبارت دیگر:
ارتفاع × (مجموع قاعدههای ذوزنقه) = مساحت متوازی الاضلاع
این رابطه را برابر با رابطه مساحت از روی شکل قرار میهیم:
ارتفاع × (مجموع قاعدههای ذوزنقه) = (مساحت یک ذوزنقه) × 2
رابطه بالا را بر حسب مساحت یک ذوزنقه بازنویسی میکنیم:
2 ÷ (ارتفاع × مجموع قاعدهها) = مساحت یک ذوزنقه
به این ترتیب، فرمول محاسبه مساحت ذوزنقه به دست میآید.
سوالات متداول در رابطه با مساحت متوازی الاضلاع
در این بخش، به برخی از سوالات پرتکرار در رابطه با مساحت متوازی الاضلاع به طور خلاصه پاسخ میدهیم.
تعریف مساحت متوازی الاضلاع چیست؟
مساحت متوازیالاضلاع، سطح یا ناحیه دوبعدی محدود به ضلعهای آن است.
واحد مساحت متوازیالاضلاع چیست؟
مساحت متوازیالاضلاع، با واحدهای مربع طول نظیر میلیمتر مربع، سانتیمتر مربع، متر مربع، اینچ مربع و غیره بیان میشود.
مساحت متوازیالاضلاع چگونه محاسبه میشود؟
مساحت متوازیالاضلاع، از ضرب قاعده در ارتفاع نظیر آن به دست میآید.
عبارت جبری مساحت متوازیالاضلاع چیست؟
فرمول ریاضی مساحت متوازیالاضلاع به صورت «S=bh» نوشته میشود. در این فرمول، S، مساحت، b، قاعده و h، ارتفاع را نمایش میدهد.
آیا امکان محاسبه مساحت متوازی الاضلاع بدون ارتفاع وجود دارد؟
بله. در صورت داشتن اندازه دو ضلع مجاور و زاویه بین آنها، یا اندازه دو قطر، میتوان مساحت متوازیالاضلاع را بدون ارتفاع به دست آورد.
عبارت جبری مساحت متوازیالاضلاع با دو ضلع چیست؟
فرمول ریاضی مساحت متوازیالاضلاع با دو ضلع برابر (S=ab×sin(y است. S، مساحت، a، یکی از ضلعها، b، ضلع مجاور و y، زاویه بین دو ضلع مجاور را نمایش میدهد.
عبارت جبری مساحت متوازیالاضلاع با قطر چیست؟
فرمول ریاضی مساحت متوازیالاضلاع با دو قطر به صورت (S=d1d2×sin(x است. S، مساحت، d1، یکی از قطرها، d2، قطر دیگر و x، یکی از زاویههای بین دو قطر را نمایش میدهد.
مساحت متوازیالاضلاع به روش برداری چگونه است؟
محاسبه مساحت متوازیالاضلاع به روش برداری، با استفاده نوشتن اندازه ضلعها یا قطرها به صورت برداری و ضرب خارجی آنها انجام میشود.
عبارت جبری مساحت متوازیالاضلاع با ضرب خارجی چیست؟
در صورت داشتن بردارهای ضلع، فرمول ریاضی مساحت متوازیالاضلاع برابر S=a×b است. در صورت مشخص بودن بردار قطرها، فرمول ریاضی مساحت متوازی الاضلاع به صورت S=(d1×d۲)÷2 نوشته میشود.
چه رابطه ای بین مساحت متوازی الاضلاع و مستطیل وجود دارد؟
اگر ارتفاع متوازیالاضلاع را از یکی از راسها رسم کنیم و مثلث به وجود آمده را به سمت دیگر متوازی الاضلاع انتقال دهیم، مستطیلی شکل میگیرد که مساحت آن (عرض × طول) با مساحت متوازیالاضلاع (ارتفاع × قاعده) برابر است.
چه رابطه ای بین مساحت متوازی الاضلاع و ذوزنقه وجود دارد؟
اگر دو ذوزنقه با اندازههای برابر را در کنار یکدیگر قرار دهیم، یک متوازی الاضلاع به وجود میآید. مساحت این متوازی الاضلاع، دو برابر مساحت هر ذوزنقه خواهد بود.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت متوازی الاضلاع — هر آنچه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- متوازی الاضلاع چیست ؟ — تعریف و مفاهیم به زبان ساده
- محیط متوازی الاضلاع چیست ؟ — به زبان ساده + حل تمرین و مثال
- فرمول محیط متوازی الاضلاع چیست ؟ — معرفی انواع فرمول ها + حل مثال
- مساحت متوازی الاضلاع چیست ؟ — فیلم آموزش رایگان + حل تمرین و مثال(همین مطلب)
- محاسبه قطر متوازی الاضلاع — فرمول های محاسبه + حل تمرین و مثال
- محیط متوازی الاضلاع به صورت جبری — فرمول های ریاضی + حل مثال
- فرمول مساحت متوازی الاضلاع چیست ؟ — تمامی فرمول ها + حل تمرین و مثال
- مساحت متوازی الاضلاع به صورت جبری — انواع فرمول ها + حل مثال
- نمونه سوال مساحت متوازی الاضلاع با جواب — حل تمرین های متنوع
- مساحت متوازی الاضلاع با قطر چگونه بدست می آید ؟ + حل مثال
- مساحت متوازی الاضلاع با سینوس — به زبان ساده + حل مثال













سلام اصول اولیه کار بااتوکد۲۰۱۳ وتبدیل ان به جی کد رامیخواهم ایا امکانش هست ضمنا ازمطالب مفیدتان تشکر میکنم
سلام، وقت شما بخیر؛
در این رابطه میتونید از مجموعه آموزشهای اتوکد فرادرس استفاده کنید.
https://faradars.org/how-to-learn/autocad
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.