متوازی الاضلاع چیست؟ — تعریف و مفاهیم به زبان ساده

در مجموعه آموزش‌های ریاضی و هندسه مجله فرادرس، برخی از شکل‌های هندسی از قبیل دایره، مثلث، مربع، مستطیل، لوزی، بیضی و ذوزنقه را معرفی کردیم. در این آموزش، می‌خواهیم با یکی دیگر از اشکال هندسی به نام متوازی الاضلاع آشنا شویم.

متوازی الاضلاع چیست ؟

«متوازی‌ الاضلاع» (Parallelogram)، همان‌گونه که از نامش نیز پیداست، یک چهارضلعی است که اضلاع روبه‌روی آن با هم موازی هستند.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

اندازه اضلاع و زوایای روبه‌رو در متوازی‌الاضلاع با هم برابر است. شکل زیر یک متوازی الاضلاع را نشان می‌دهد که پیکان‌های روی اضلاع موازی بودن ضلع‌های مقابلِ هم را مشخص کرده‌اند.

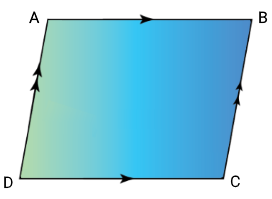
• ضلع متوازی‌الاضلاع: در شکل بالا، $$AB$$، $$BC$$، $$CD$$ و $$DA$$ ضلع‌های متوازی الاضلاع هستند.
• رأس متوازی‌الاضلاع: در شکل بالا $$A$$، $$B$$، $$C$$ و $$D$$ رأس نامیده می‌شوند که محل برخورد دو ضلع هستند.

متوازی الاضلاع شکل زیر را در نظر بگیرید. با توجه به این شکل، چند مورد از اصطلاحات مربوط به این شکل هندسی را بیان می‌کنیم.

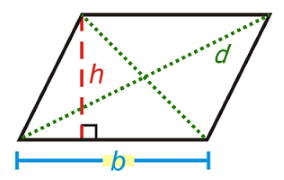
• قاعده متوازی‌الاضلاع: در متوازی الاضلاع شکل بالا fhgh، $$b$$ قاعده است که معمولاً (نه همیشه) در قسمت پایین و کف شکل در نظر گرفته می‌شود.
• ارتفاع متوازی‌الاضلاع: $$h$$ ارتفاع است که در واقع، خطی است که از قاعده بالا بر قاعده پایین عمود می‌شود.
• قطر متوازی‌الاضلاع: $$d$$ یکی از دو قطر متوازی‌الاضلاع است که دو رأس مقابل را به هم وصل می‌کند.

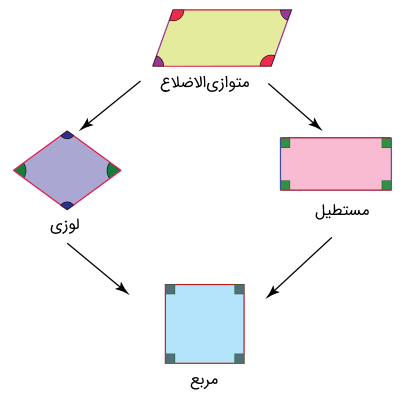
نکته: مستطیل، لوزی و مربع همه نوعی متوازی الاضلاع هستند، زیرا با توجه به تعریفی که گفتیم، هم چهار ضلع دارند و هم اضلاع آن‌ها دو به دو موازی هستند. مربع و مستطیل متوازی‌الاضلاع‌هایی هستند که چهار زاویه قائمه دارند.

ویژگی های متوازی الاضلاع

متوازی الاضلاع $$\text{ABDC}$$ شکل زیر را در نظر بگیرید.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

با توجه به این شکل، ویژگی‌های مختلف متوازی الاضلاع را بیان می‌کنیم.

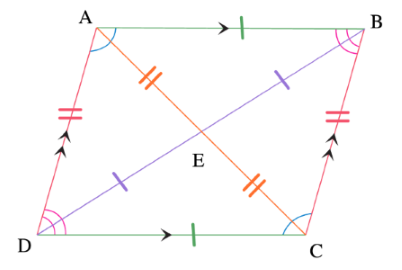
• اضلاع روبه‌رو (مقابل) یک متوازی الاضلاع موازی هم هستند:

$$\large A B\|D C \text{ , } \;\;\; AD\| B C$$

• اندازه اضلاع روبه‌رو (مقابل) یک متوازی الاضلاع با هم برابر است:

$$\large A B= D C \text{ , } \;\;\; AD= B C$$

• زاویه‌های مقابل یک متوازی الاضلاع با هم برابرند:

$$\large \angle A = \angle C \text{ , }\;\;\;\angle B = \angle D$$

• قطرهای متوازی الاضلاع یکدیگر را نصف می‌کنند:

$$\large D E = E B \text{ , } \;\;\;AE = EC$$

• مجموع زوایای مجاور در متوازی الاضلاع برابر با ۱۸۰ درجه است (مکمل هم هستند):

$$\large \begin {align*} \angle ADC + \angle DCB & =180 ^\circ \\ \angle DCB + \angle CBA & = 180 ^\circ \\ \angle CBA + \angle BAD & = 180 ^\circ \\ \angle BAD + \angle ADC & = 180 ^\circ \end {align*}$$

• هر قطر متوازی الاضلاع، آن را به دو مثلث هم‌نهشت تبدیل می‌کند:

$$\Delta \text{DAB}$$ هم‌نهشت $$\Delta \text{BCD}$$ است.

$$\Delta \text{DAC}$$ هم‌نهشت $$\Delta \text{BCA}$$ است.

قضیه های متوازی الاضلاع

در این بخش، چند قضیه مربوط به متوازی‌الاضلاع را بیان می‌کنیم.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

قضیه اول متوازی الاضلاع

در یک متوازی‌الاضلاع، اضلاع مقابل برابرند. برعکس این قضیه نیز برقرار است؛ اگر در یک چهارضلعی اضلاع مقابل دو به دو برابر باشند، آن شکل متوازی‌الاضلاع است.

اثبات: شکل زیر را در نظر بگیرید.

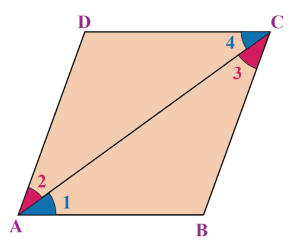
در مثلث‌های $$\Delta ABC$$ و $$\Delta CDA$$، داریم:

$$\large \begin{align} AC&=AC \\ \angle 1&=\angle 4 \\ \angle 2&=\angle 3 \end {align}$$

با توجه به برابر بودن دو زاویه و ضلع بین آن‌ها، دو مثلث با معیار دو زاویه و ضلع بین (ز ض ز) همنهشت هستند و این یعنی اضلاع باید برابر باشند:

$$\large \begin{align}{AB=DC\;\text{,}\;\;\;AD=BC} \end{align}$$

این یعنی اضلاع مقابل برابرند.

قضیه دوم متوازی الاضلاع

در یک متوازی‌الاضلاع، زاویه‌های مقابل با هم برابرند. برعکس این قضیه نیز برقرار است؛ اگر در یک چهارضلعی زاویه‌های مقابل دو به دو برابر باشند، آن شکل متوازی‌الاضلاع است.

اثبات: شکل زیر را در نظر بگیرید.

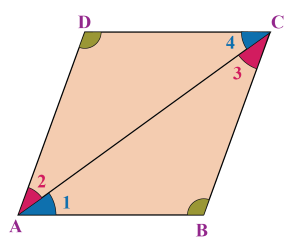
در مثلث‌های $$\Delta ABC$$ و $$\Delta CDA$$، داریم:

$$\large \begin{align} AC&=AC \\ \angle 1&=\angle 4 \\ \angle 2&=\angle 3 \end {align}$$

با توجه به برابر بودن دو زاویه و ضلع بین آن‌ها، دو مثلث با معیار دو زاویه و ضلع بین (ز ض ز) همنهشت هستند و این یعنی زاویه‌ها باید برابر باشند:

$$\large \begin{align}{ \angle B =\angle D } \end {align}$$

به طور مشابه، داریم:

$$\large \begin{align}{ \angle A =\angle C } \end {align}$$

این یعنی زاویه‌های مقابل برابرند.

قضیه سوم متوازی الاضلاع

در یک متوازی‌الاضلاع، قطرها یکدیگر را نصف می‌کنند. برعکس این قضیه نیز برقرار است؛ اگر در یک چهارضلعی قطرها یکدیگر را نصف کنند، آن شکل متوازی‌الاضلاع است.

اثبات: شکل زیر را در نظر بگیرید.

در مثلث‌های $$\Delta AEB$$ و $$\Delta DEC$$، داریم:

$$\large \begin{align} AB&=CD \\ \angle 1&=\angle 3 \\ \angle 2&=\angle 4 \end {align}$$

با توجه به برابر بودن دو زاویه و ضلع بین آن‌ها، دو مثلث با معیار دو زاویه و ضلع بین (ز ض ز) همنهشت هستند و این یعنی داریم:

$$\large \begin{align}{AE=EC\;\text{,}\;\;\;BE=ED} \end{align}$$

بنابراین، دو قطر یکدیگر را نصف می‌کنند.

قضیه چهارم متوازی الاضلاع

در یک چهارضلعی، اگر یکی از جفت ضلع مقابل برابر و موازی باشند، آنگاه آن شکل یک متوازی الاضلاع است.

اثبات: شکل زیر را در نظر بگیرید.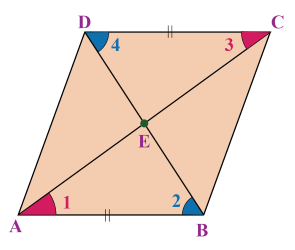

در مثلث‌های $$\Delta AEB$$ و $$\Delta DEC$$، داریم:

$$\large \begin{align} AB&=CD \\ \angle 1&=\angle 3 \\ \angle 2&=\angle 4 \end {align}$$

با توجه به برابر بودن دو زاویه و ضلع بین آن‌ها، دو مثلث با معیار دو زاویه و ضلع بین (ز ض ز) همنهشت هستند و این یعنی داریم:

$$\large \begin{align}{AE=EC\;\text{,}\;\;\;BE=ED} \end{align}$$

بنابراین، قطرهای $$AC$$ و $$BD$$ یکدیگر را نصف می‌کنند و این یعنی $$ABCD$$ یک متوازی‌الاضلاع است.

مساحت متوازی الاضلاع

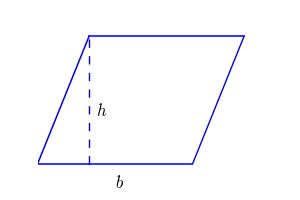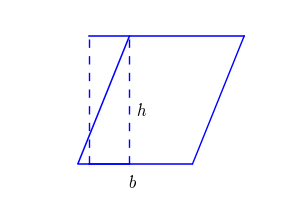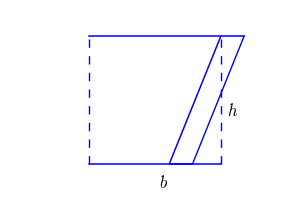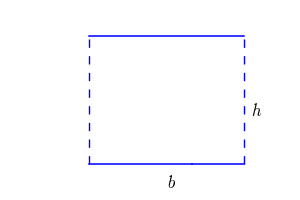
به زبان ساده، مساحت متوازی‌الاضلاع برابر است با حاصل‌ضرب قاعده در ارتفاع. برای درک بهتر، به تصویر زیر دقت کنید. اگر ارتفاع را رسم کنید، یک مثلث در شکل ایجاد خواهد شد که با انتقال مثلث به سمت دیگر، متوازی الاضلاع به مستطیل تغییر شکل خواهد داد.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

می‌دانیم که مساحت مستطیل از حاصل‌ضرب طول در عرض به دست می‌آید که در اینجا عرض، همان ارتفاع رسم شده است. بنابراین چنانچه $$A$$ مساحت، $$b$$ اندازه قاعده و $$h$$ ارتفاع باشد، فرمول مساحت متوازی‌الاضلاع به صورت زیر خواهد بود:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

$$\large A = b \times h$$

در صورت تمایل به یادگیری بیشتر راجع به مساحت متوازی الاضلاع، مطالعه مطالب زیر از مجله فرادرس را به شما پیشنهاد می‌کنیم:

• مساحت متوازی‌الاضلاع به صورت جبری — انواع فرمول‌ها + حل مثال
• نمونه سوال مساحت متوازی‌الاضلاع با جواب — حل تمرین‌های متنوع
• مساحت متوازی‌الاضلاع با قطر چگونه بدست می‌آید؟ + حل مثال
• مساحت متوازی‌الاضلاع با سینوس — به زبان ساده + حل مثال

محیط متوازی الاضلاع

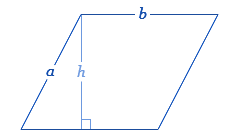
برای محاسبه محیط متوازی‌الاضلاع باید اندازه چهار ضلع را با هم جمع کنیم. از آنجا که اضلاع مقابل برابر هستند، برای متوازی‌الاضلاعی با اضلاع $$a$$ و $$b$$، محیطِ $$P$$ برابر است با:

(مجموع دو ضلع مجاور) × ۲ = محیط متوازی‌الاضلاع

$$\large \boxed {P = a + a + b + b = 2 a + 2 b = 2 (a+b)}$$

برای آشنایی بیشتر با نحوه محاسبه محیط متوازی‌الاضلاع، مطالعه مطالب زیر از مجله فرادرس را به شما پیشنهاد می‌‌کنیم:

• فرمول محیط متوازی‌الاضلاع چیست؟ — معرفی انواع فرمول‌ها + حل مثال
• محیط متوازی‌الاضلاع به صورت جبری — فرمول‌های ریاضی + حل مثال

مثال های متوازی الاضلاع

در این بخش، چند مثال را از متوازی الاضلاع بررسی می‌کنیم.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

مثال اول متوازی الاضلاع

محیط متوازی‌الاضلاع زیر برابر با ۱۶ سانتی‌متر است. اگر اندازه ضلع $$b$$ آن برابر با ۵ سانتی‌متر باشد، اندازه ضلع $$a$$ را به دست آورید.

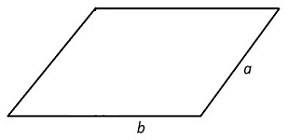
حل: از فرمول محیط متوازی الاضلاع استفاده می‌کنیم و اندازه ضلع $$a$$ را محاسبه می‌کنیم:

$$\large P = 2 a + 2 b \Rightarrow 16 = 2a + 2 (5)\Rightarrow 2a = 6 \Rightarrow a = 3 \, \text{cm}$$

مثال دوم متوازی الاضلاع

مساحت متوازی الاضلاع شکل زیر را به دست آورید.

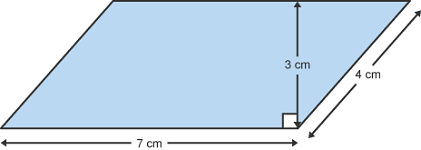
حل: با توجه به اینکه طول یک ضلع (۷ سانتی‌متر) و ارتفاع عمود بر آن (۳ سانتی‌متر) را داریم، به راحتی، می‌توانیم مساحت متوازی الاضلاع را محاسبه کنیم:

$$\large A={7~\text {cm}}\times{3~ \text{cm}}={21~\text {cm}}^{2}$$