بیضی چیست؟ | تعریف و مفاهیم به زبان ساده

در آموزش‌های قبلی مجله فرادرس، برخی از شکل‌های هندسی از قبیل دایره، مثلث، مربع، مستطیل، لوزی، متوازی الاضلاع و ذوزنقه را معرفی کردیم. در این آموزش، می‌خواهیم با یکی دیگر از اشکال هندسی به نام بیضی آشنا شویم.

بیضی چیست؟

ماهواره‌های در حال چرخش، زمین که به دور خورشید می‌چرخد و ماه که به دور ما می‌چرخد، نمونه‌هایی از مواردی هستند که مسیرهای بیضوی را طی می‌کنند.

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

علاوه بر این اجرام آسمانی، بسیاری از ساختمان‌ها و پل‌ها، به منظور استحکام و زیبایی، ساختاری بیضی‌ شکل دارند.

به همین دلیل است که برای درک بسیاری از پدیده‌های طبیعی و طراحی ساختارهایی که در آن‌ها شکل بیضی وجود دارد، باید درک مناسبی از این شکل داشته باشیم. اولین چیزی که از ظاهر یک بیضی مشاهده می‌کنیم، این است که به شکل یک دایره فشرده به نظر می‌رسد. در ادامه، رابطه بین بیضی‌ و دایره را بیان می‌کنیم.

بیضی چیست؟

از منظر مقاطع مخروطی، «بیضی» (Ellipse) یکی از مقاطع مخروطی است که از تقاطع مخروط با صفحه‌ای که نسبت به قاعده مخروط زاویه دارد، ساخته می‌شود. شکل زیر این موضوع را به خوبی نشان می‌دهد.

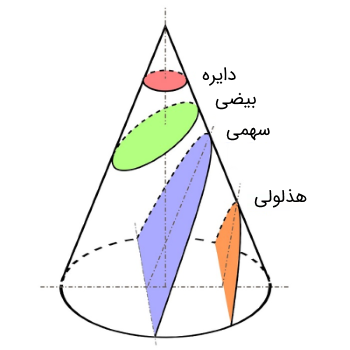
اگر بخواهیم از منظر مکان هندسی بحث کنیم، بیضی‌‌ مجموعه تمام نقاطی در صفحه است که مجموع فاصله آن‌ها از دو نقطه ثابت (که کانون نامیده می‌شوند) یک مقدار ثابت است. در شکل زیر، F و G کانون‌های بیضی هستند و P نقطه‌ای از مکان هندسی بیضی است.

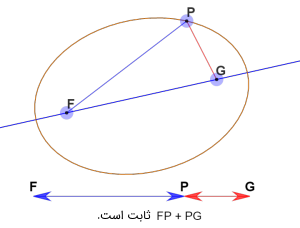
صورت صحیح جمله‌ای که درباره ارتباط دایره و بیضی گفتیم، این است: دایره یک بیضی است که کانون‌های آن در یک نقطه قرار دارند و آن نقطه همان مرکز است. در واقع، در دایره، همواره فاصله از F تا P و از P تا G ثابت و یکسان است. به‌ عبارت‌ دیگر، اگر از نقطه F به هر نقطه‌ای روی محیط بیضی و سپس از آن نقطه به نقطه G برویم، همواره مسافت یکسانی طی خواهیم کرد.

مشخصات بیضی

مشخصات بیضی شامل پارامترهایی است که بیضی با آن‌ها تعریف می‌شود.

این موارد در شکل زیر نشان داده شده‌اند.

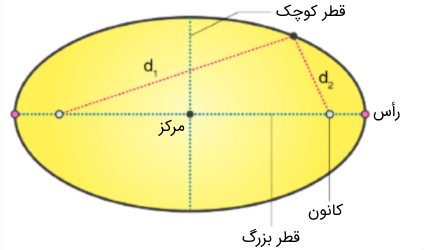
محور اصلی یا بزرگ، طولانی‌ترین قطر بیضی‌ است که از یک رأس بیضی‌ و از طریق مرکز به رأس دیگر آن می‌رود و از عریض‌ترین قسمت بیضی، رد می‌شود. محور کوچک، کوتاه‌ترین قطر (در باریک‌ترین قسمت بیضی) است. هر یک از نیم‌محورهای بیضی، خط تقارن آن نیز هستند. همچنین، هر بیضی‌ بی‌نهایت قطر دارد.

همان‌طور که در شکل زیر نشان داده شده، نیم‌محور اصلی نیز، نیمی از محور اصلی است و نیم‌محور کوچک، نصف محور کوچک.

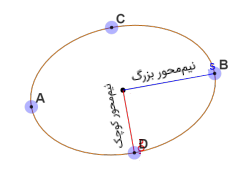
مرکز بیضی نیز محل برخورد قطر بزرگ و قطر کوچک است.

رسم بیضی

برای رسم بیضی، می‌توانید دو سنجاق را روی تخته یا مقوا قرار دهید، سپس یک حلقه نخ را دور دو سنجاق بپیچید. پس از آن، یک مداد را درون حلقه قرار دهید و نخ را به کمک مداد آنقدر بکشید تا شکل یک مثلث به خود بگیرد.

فیلم آموزش هندسه 3 – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

شروع کنید به غلتاندن مداد روی کاغذ طوری که یک منحنی کشیده شود و این کار را تا آنجا ادامه دهید تا یک بیضی شکل گیرد. دلیل این امر آن است که نخ به طور طبیعی فاصله یکسانی را از سنجاق تا مداد و از مداد تا سنجاق دیگر طی می‌کند.

همان‌طور که گفتیم، دایره نیز نوعی بیضی است. در حقیقت، دایره یک بیضی است که هر دو کانون آن در یک نقطه (مرکز) قرار گرفته‌اند. شکل زیر این موضوع را به خوبی نشان می‌دهد.

معادله بیضی

معادله بیضی در حالتی که a برابر b باشد به شکل معادله دایره درمی‌آید.

فیلم آموزش ریاضی عمومی ۲ + حل مثال در فرادرس

کلیک کنید

بیضی شکل زیر را در نظر بگیرید.

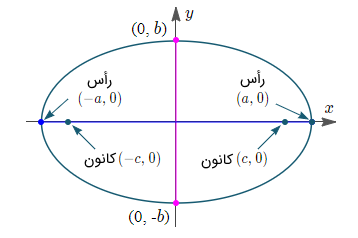
معادله این بیضی‌ با محور اصلی (بزرگ) افقی به صورت زیر بیان می‌شود:

$$\large \frac { { x } ^ { 2 } } { { a } ^ { 2 } } + \frac { { y } ^ { 2 } } { { b } ^ { 2 } } = { 1 }$$

که در آن، $$a$$ فاصله مرکز از انتهای محور بزرگ و $$b$$ فاصله مرکز از انتهای محور کوچک است. در واقع، $$a$$ طول نیم‌محور بزرگ و $$b$$ طول نیم‌محور کوچک است. کانون‌ها در نقاط $$(-c,0)$$ و $$( c , 0 )$$ واقع شده‌اند، که $$c$$ برابر است با:

$$\large { c } = \sqrt { {{ a } ^ { 2 } - { b } ^ { 2 } } }$$

اگر بیضی عمودی باشد (نیم‌محور بزرگ آن عمودی باشد)، معادله بیضی به صورت زیر خواهد بود:

$$\large \frac { { x } ^ { 2 } } { { b } ^ { 2 } } + \frac { { y } ^ { 2 } } { { a } ^ { 2 } } = { 1 }$$

مساحت بیضی

فرض کنید اندازه نیم‌قطر (نیم‌محور) بزرگ یک بیضی‌ برابر با $$a$$ و نیم‌قطر (نیم‌محور) کوچک آن $$b$$ باشد.

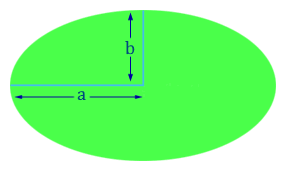
فرمول مساحت بیضی‌ به صورت زیر است:

$$\large  { A = \pi a b }$$

همان‌طور که می‌بینیم، اگر دو نیم‌قطر برابر باشند، فرمول مساحت، همان فرمول مساحت دایره خواهد شد. برای آشنایی بیشتر با مبحث مساحت بیضی، مطالعه مطالب زیر را به شما پیشنهاد می‌کنیم:

• (+) مساحت بیضی با انتگرال — اثبات فرمول به زبان ساده
• (+) محاسبه آنلاین مساحت بیضی — معرفی بهترین سایت‌ها
• (+) فرمول مساحت بیضی — به زبان ساده

محیط بیضی

ارائه یک فرمول دقیق برای محاسبه محیط بیضی کار نسبتاً دشواری است. البته چندین فرمول‌ تقریبی برای محاسبه محیط ارائه شده است.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

یکی از معروف‌ترین تقریب‌های محیط بیضی، فرمولی است که اویلر آن را ارائه کرد:

$$\large P \approx \pi \sqrt { 2 ( a ^ 2 + b ^ 2 ) }$$

یکی دیگر از معروف‌ترین تقریب‌های محیط بیضی‌ را رامانوجان، ریاضیدان معروف هندی، پیشنهاد کرده است:

در فرمول‌های بالا، $$a$$ طول نیم‌قطر بزرگ و $$b$$ طول نیم‌قطر کوچک بیضی‌ است. برای آشنایی بیشتر با مبحث محیط بیضی، مطالعه مطالب زیر را به شما پیشنهاد می‌کنیم:

• (+) محاسبه آنلاین محیط بیضی — معرفی بهترین سایت‌ها
• (+) فرمول محیط بیضی چیست؟ — معرفی ۹ فرمول پرکاربرد

خروج از مرکز بیضی

خروج از مرکز بیضی، معیاری برای نشان دادن کشیدگی آن است. اگر خروج از مرکز به مقدار 0 نزدیک باشد، بیضی دایره‌ای‌تر می‌شود و اگر به 1 نزدیک شود، بیضی کشیده‌تر خواهد شد. خروج از مرکز با فرمول زیر به دست می‌آید:‌

$$\large \frac c a$$ = خروج از مرکز

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

خط مماس بر بیضی

خط مماس، خطی است که یک منحنی را فقط در یک نقطه لمس می‌کند، بدون اینکه آن را قطع کند. در شکل زیر یک خط مماس را روی یک بیضی مشاهده می‌کنید.

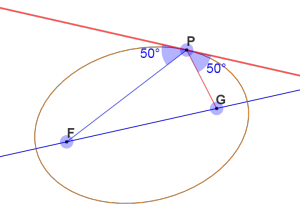
خط مماس در نقطه P زوایای برابری با دو خطی که از هر کانون و نقطه P می‌گذرند، دارد. اگر سعی کنیم دو نقطه کانونی را روی هم قرار دهیم، بیضی‌ به دایره تبدیل خواهد شد و آن ۵۰ درجه‌های به ۹۰ درجه تبدیل می‌شوند.

مثال‌های بیضی

در این بخش، چند مثال را در رابطه با بیضی بررسی می‌کنیم.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

مثال اول بیضی

شکل و مشخصات یک بیضی‌ را با معادله زیر مشخص رسم و مشخص کنید.

$$\large \frac { { x } ^ { 2 } } { { 1 0 0 } } + \frac {{ y } ^ { 2 } } { { 6 4 } } = { 1 }$$

حل: با توجه به فرمولی که برای معادله بیضی گفتیم، $$a ^ 2 = 100$$ و در نتیجه، $$a = \pm 10$$ است. در نتیجه، رأس‌های بیضی در نقاط $$(-10 , 0 )$$ و $$(10 , 0 )$$ قرار دارند. اکنون، برای تعیین مکان کانون‌ها، داریم:

$$\large { c } = \sqrt { { {a } ^ { 2 } - { b } ^ { 2 } } } = \sqrt { { { 1 0 0 } - { 6 4 } } } = \sqrt { { 3 6 } } = 6$$

بنابراین، کانون‌ها در نقاط $$(-6,0)$$ و $$( 6 , 0 )$$ واقع شده‌اند.

شکل این بیضی به صورت زیر است:

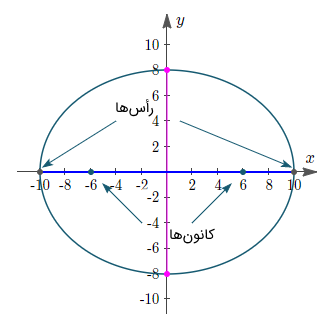
مثال دوم بیضی

معادله یک بیضی را به دست آورید که طول محور کوچک آن ۸ بوده و یک رأس آن در نقطه $$(0, - 5 )$$ قرار داشته باشد. محور بزرگ بیضی عمودی است.

حل: با توجه به اطلاعات مسئله، بیضی به شکل زیر خواهد بود.

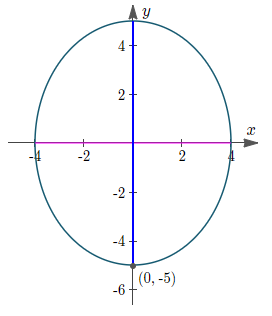
با توجه به شکل بالا، $$a = 5$$ و $$b = 4$$ است. بنابراین، معادله بیضی‌ به صورت زیر خواهد بود:

$$\large \frac { { x } ^ { 2 } } { { 1 6 } } + \frac { { y } ^ { 2 } } { {2 5 } } = { 1 }$$

مثال سوم بیضی

مساحت بیضی‌‌ شکل زیر را محاسبه کنید.

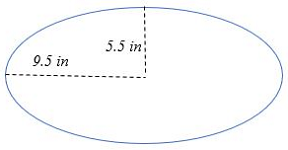
حل: با توجه به اینکه $$a = 9.5\; \text{in}$$ و $$5.5\; \text{in}$$ را داریم، مساحت بیضی‌‌ به سادگی به دست می‌آید:

$$\large A = \pi ab=3.14\times 9.5\times 5.5 = 164.065 \; \text{in} ^2$$