حجم منشور و فرمول محاسبه آن — به زبان ساده

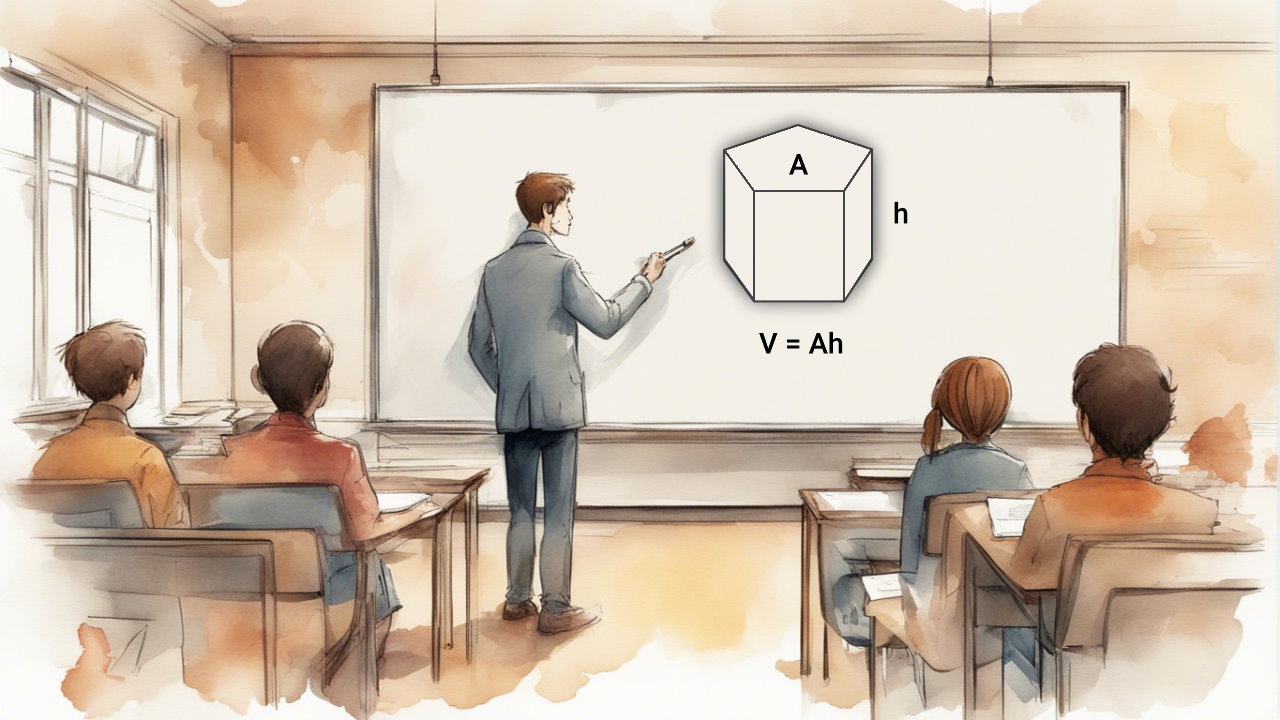
در آموزش‌های قبلی مجله فرادرس، با روش‌های محاسبه حجم برخی از احجام هندسی از قبیل کره، مخروط و استوانه آشنا شدیم. در این آموزش با روش محاسبه حجم منشور آشنا می‌شویم.

منشور چیست؟

منشور شکلی است سه‌بعدی که دو وجه از وجوه آن مشابه هستند و آن‌ها را «قاعده» می‌نامیم.

فیلم آموزش ریاضی پایه هفتم – جامع و با نکات مهم در فرادرس

کلیک کنید

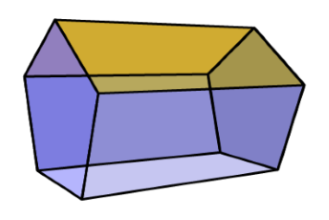
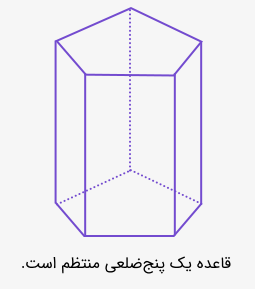
قاعده‌های منشور می‌توانند مثلث، مربع، مستطیل یا هر چندضلعی دیگری باشند. سایر وجه‌های منشور مستطیل یا متوازی‌الاضلاع هستند. دقت کنید که قاعده‌های منشور انحنا ندارند و باید چندضلعی باشند. شکل زیر یک منشور را نشان می‌دهد که قاعده آن پنج‌ضلعی است.

سطح مقطع منشور

سطح مقطع یک جسم هندسی شکلی است که با برش مستقیم آن حاصل می‌شود.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

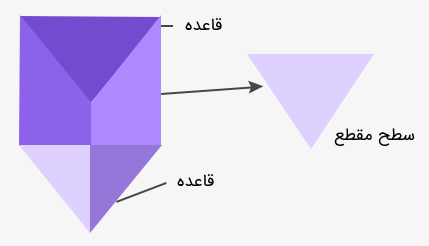
سطح مقطع همچنین به عنوان تقاطع یک صفحه با یک جسم سه‌بعدی در نظر گرفته می‌شود. سطح مقطع یک منشور موازی با قاعده آن است. شکل زیر یک منشور مثلثی را نشان می‌دهد.

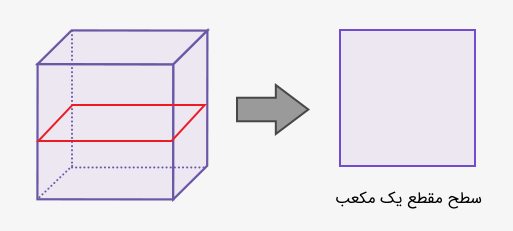
یک منشور مربعی نیز در شکل زیر نشان داده شده است.

منشور منتظم و منشور نامنتظم

قاعده یک منشور می‌تواند یک چند ضلعی منتظم یا چندضلعی نامنتظم باشد. بسته به شکل قاعده، منشورها در دو دسته منتظم و نامنتظم دسته‌بندی می‌شوند.

شکل زیر یک منشور منتظم را نشان می‌دهد.

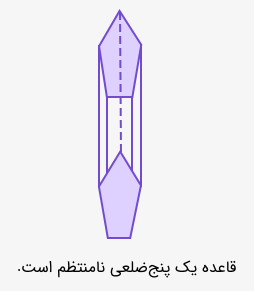
در شکل زیر نیز یک منشور نامنتظم نشان داده شده است.

منشور قائم و منشور مایل

وقتی دو قاعده یک منشور کاملاً تراز باشند و وجوه (پهلوها) آن بر قاعده‌ها عمود باشند، منشور قائم است. از سوی دیگر، اگر وجه ها بر قاعده‌ها عمود نباشند، یک منشور مایل خواهیم داشت.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

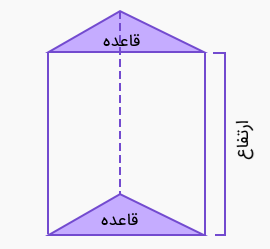
شکل زیر یک منشور قائم را نشان می‌دهد.

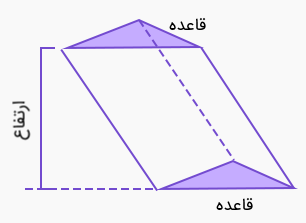
یک منشور مایل نیز در شکل زیر نشان داده شده است.

مساحت سطح منشور

سطح مقطع یک منشور مقدار مساحت (ناحیه‌ای) است که همه وجه‌های منشور اشغال می‌کنند. برای مثال، همه وجه‌های یک منشور مثلثی در شکل زیر باز شده‌اند. می‌بینیم که سطوح شامل دو مثلث و سه مستطیل هستند.

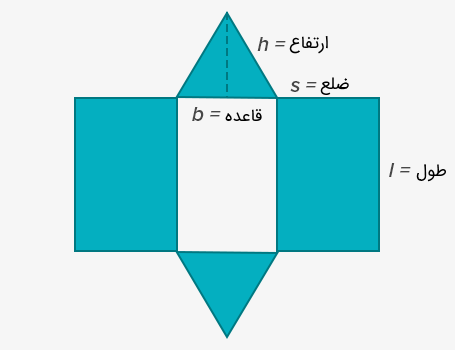
اگر بخواهیم مساحت جانبی منشور را محاسبه کنیم، باید این‌گونه بنویسیم:

مساحت وجه‌ها یا همان پهلوها + مساحت مثلث‌های قاعده = مساحت سطح منشور

بنابراین، با توجه به اطلاعات شکل بالا، خواهیم داشت:

$$\large A = 2 (\frac 12\times b\times h ) + 2 (l \times s) + (l\times b) = bh+2ls+lb$$

حجم منشور

حجم منشور نیز مقدار فضایی است که درون منشور وجود دارد. حجم منشور از حاصل‌ضرب مساحت قاعده در ارتفاع به دست می‌آید:

ارتفاع × مساحت قاعده = حجم منشور 

فیلم آموزش ریاضی پایه هفتم – جامع و با نکات مهم در فرادرس

کلیک کنید

فرمول حجم منشور مثلثی

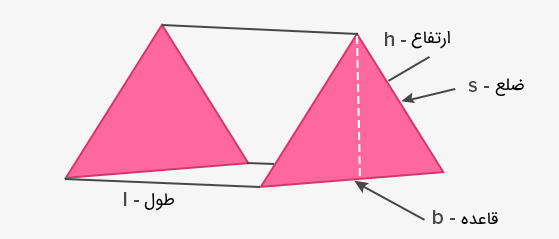
منشور مثلثی شکل زیر را در نظر بگیرید. با توجه به فرمول حجم منشور که گفتیم، حجم منشور مثلثی با توجه به شکل زیر برابر خواهد بود با:

$$\boxed { \large V = (\frac 12 b h )\times (l )= \frac 12 b h l }$$

فرمول حجم منشور مستطیلی

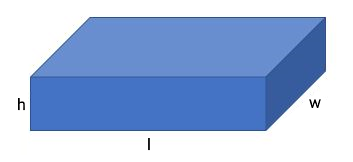
منشور زیر را در نظر بگیرید که ارتفاع آن $$h$$ و طول و عرض قاعده آن به ترتیب $$l$$ و $$w$$ هستند. فرمول مساحت این منشور به صورت زیر است:

$$\boxed { \large V = ( l w )\times ( h )=l w h }$$

فرمول حجم منشور مایل

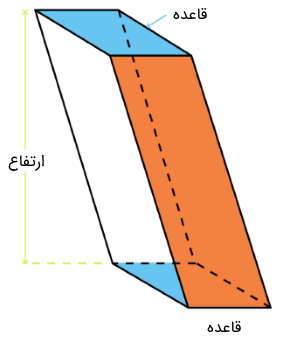
حجم منشور مایل نیز با حاصل‌ضرب مساحت قاعده در ارتفاع به دست می‌‌آید. در شکل زیر، حجم منشور از فرمول زیر به دست می‌آید:

ارتفاع × مساحت قاعده = حجم منشور مایل

مثال های محاسبه حجم منشور

در این بخش، چند مثال را از محاسبه حجم منشور بررسی می‌کنیم.

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

مثال اول محاسبه حجم منشور

حجم منشور زیر را به دست آورید.

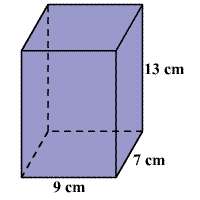
حل: همان‌طور که می‌دانیم، فرمول محاسبه حجم منشور $$V = Bh$$ است که در آن، $$B$$ مساحت قاعده و $$h$$ ارتفاع منشور است. در شکل بالا، قاعده منشور یک مستطیل است با طول $$l$$ و عرض $$w$$ که مساحت آن با رابطه $$B = l w$$ به دست می‌آید:

$$\large B = l\times w = 9 \times 7 = 63\; \text{cm}^2$$

با توجه به اینکه ارتفاع منشور $$h = 13\; \text{cm}$$ است، حجم منشور برابر خواهد بود با:‌

$$V = B \times h = 63 \times 13 = 819\; \text{cm} ^ 3$$

در نتیجه، حجم منشور مساوی با ۸۱۹ سانتی‌متر مکعب است.

مثال دوم محاسبه حجم منشور

حجم منشور زیر را به دست آورید.

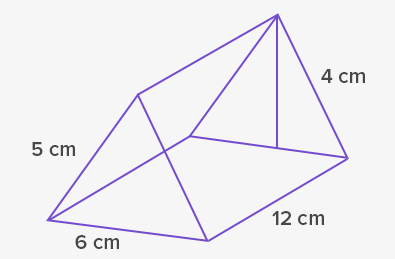
حل: قاعده این منشور یک مثلث است و برای محاسبه آن باید مساحت آن را به دست آوریم. همان‌طور که در شکل می‌بینیم، ارتفاع مثلث برابر با ۴ سانتی‌متر و قاعده آن ۶ سانتی‌متر است. بنابراین، مساحت قاعده منشور که همان مساحت مثلث است، برابر است با:

$$\large A = \frac 12 \times 4 \times 6 = 12 \; \text{cm}^2$$

با توجه به اینکه اندازه ارتفاع ۱۲ سانتی‌متر است، حجم منشور به شکل زیر محاسبه می‌شود:

$$\large V = 12 \times 12 = 144\; \text{cm}^ 3$$

مثال سوم محاسبه حجم منشور

حجم منشور زیر را به دست آورید.

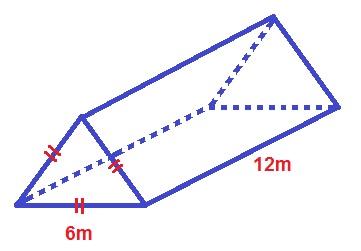
حل: قاعده این منشور یک مثلث متساوی‌الاضلاع با ضلع ۶ متر است. همان‌طور که در مطلب «مساحت مثلث متساوی الاضلاع | محاسبه به زبان ساده» از مجله فرادرس دیدیم، اگر طول هر ضلع این مثلث را برابر با $$a$$ در نظر بگیریم، مساحتش برابر خواهد بود با

$$\large A = \frac {\sqrt 3}{4} a ^ 2 = \frac {\sqrt 3}{4} \times 6^ 2 = 9 \sqrt 3 \; \text{m}^ 2$$

با توجه به اینکه اندازه ارتفاع ۱۲ سانتی‌متر است، حجم منشور برابر است با

$$\large V = 9 \sqrt 3 \times 12 = 108 \; \text{m}^3$$