چگونه محیط مربع را حساب کنیم؟ + فیلم آموزشی و حل تمرین

رابطه کلی محیط مربع برابر «یک ضلع ضربدر چهار» است. البته امکان تعیین محیط این شکل چهار ضلعی با استفاده از قطر آن نیز وجود دارد. مفهوم محیط در بسیاری از فعالیتها نظیر مهندسی، معماری، طراحی و غیره به کار برده میشود. در این آموزش، به معرفی روشهای محاسبه محیط مربع با ضلع و قطر به همراه چند مثال کاربردی میپردازیم.
فیلم آموزشی محاسبه محیط مربع
مربع چیست؟
مربع، یک شکل چند ضلعی است که از چهار ضلع با اندازههای برابر و چهار راس با زاویه 90 درجه تشکیل میشود. تصویر زیر، نمونهای از یک مربع را نمایش میدهد.
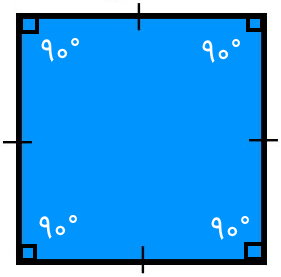
به پاره خط اتصال دهنده دو راس رو به رویی مربع، قطر مربع گفته میشود. این پاره خط نیز مانند ضلع، در محاسبه محیط و مساحت مربع مورد استفاده قرار میگیرد. مربع دارای دو قطر برابر است.

محیط چیست؟
به اندازه خط تشکیل دهنده یک شکل هندسی بسته، محیط میگویند. مربع، مستطیل، لوزی، دایره، متوازی الاضلاع و مثلث، از شناخته شدهترین شکلهای منتظم بسته هستند.

محیط مربع چیست ؟
محیط مربع، مجموع طول ضلعهای تشکیل دهنده این شکل هندسی است. به عنوان مثال، مربع مشابه تصویر زیر را بر روی کاغذ رسم کنید.
سپس، قلم خود را بر روی نقطه شماره 1 قرار داده و آن را به طور پیوسته در مسیر نقاط 2، 3، 4 و 1 حرکت دهید. هنگام بازگشت به نقطه 1، طول مسیر طی شده توسط قلم، همان محیط مربع است.
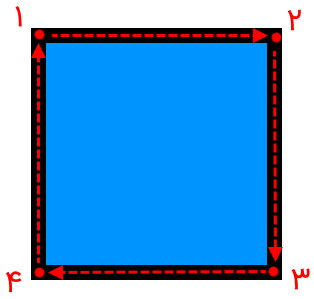
با توجه به تعریف و تصویر بالا، رابطه محیط مربع با ضلعهای آن را میتوان به صورت زیر نوشت:
جمع تمام ضلعها = محیط
ضلع + ضلع + ضلع + ضلع = محیط مربع
ضلع مربع 4 = محیط مربع
بر اساس رابطه بالا، طول ضلع مربع به محیط آن برابر یکچهارم است.
محیط مربع چگونه بدست می آید ؟
محیط مربع، از ضرب طول یک ضلع آن در عدد 4 به دست میآید. البته امکان محاسبه محیط با قطر آن نیز وجود دارد که در بخشهای بعدی به معرفی روش و فرمول آن خواهیم پرداخت.
مثال: محاسبه محیط قاب پنجره
قاب پنجره زیر به شکل مربع ساخته شده است. اگر طول یکی از ضلعهای قاب پنجره برابر 1 متر باشد، محیط قاب پنجره چقدر خواهد بود؟

فرمول محیط مربع به صورت زیر نوشته میشود:
ضلع مربع 4 = محیط مربع
به این ترتیب:
ضلع قاب 4 = محیط قاب پنجره
1 4 = محیط قاب پنجره
4 = محیط قاب پنجره
محیط قاب پنجره بالا برابر 4 متر است.
علامت اختصاری محیط چیست؟
در ریاضیات، محیط مربع و دیگر شکلهای هندسی با حرف انگلیسی P نمایش داده میشود. این حرف، ابتدای کلمه «Perimeter» به معنای «محیط» است. حرف انگلیسی a به منظور نمایش طول ضلع مربع و حرف انگلیسی d جهت نشان دادن قطر مربع مورد استفاده قرار میگیرد.
محیط مربع به صورت جبری چیست؟
عبارت جبری فرمول محیط مربع با ضلع به شکل زیر است:
- P: محیط
- a: طول ضلع
فرمول محیط مربع با قطر به صورت زیر نوشته میشود:
- P: محیط
- d: قطر
واحد اندازه گیری محیط چیست؟
در سیستم بین المللی (متریک)، محیط مربع و دیگر شکلهای هندسی، با واحدهایی نظیر میلیمتر، سانتیمتر، متر و غیره بیان میشود.
کاربرد محیط مربع چیست؟
محیط مربع و دیگر شکلهای هندسی، از مفاهیم پرکاربرد در زندگی روزمره و حرفههایی نظیر مهندسی، معماری و طراحی گرافیکی است. به عنوان مثال، در صورت نیاز به درزبندی در اطراف پنجرههای خانه، باید میزان درزگیر مورد نیاز محاسبه شود. این محاسبات با استفاده از مفهوم محیط انجام میگیرد. مربع در کنار دایره و مثلث، از ابتداییترین شکلهای موجود در طبیعت و محیط اطراف ما است. از اینرو، یادگیری نحوه محاسبه محیط آن، اهمیت بالایی در حوزههای مختلف دارد.

حل مثال های کاربردی محیط
در این بخش، چند مثال کاربردی را تشریح میکنیم.
مثال اول: تعیین محیط با جمع ضلعها
مربعی با طول 9 را در نظر بگیرید. محیط این مربع چقدر است؟
مثالهای محاسبه محیط، با استفاده از فرمول و بدون شکل نیز قابل حل هستند. با این وجود، رسم شکل میتواند باعث درک بهتر مسئله شود. به همین دلیل، ابتدا یک مربع را رسم میکنیم و یکی از ضلعهای آن را با طول ضلع مشخص میکنیم.
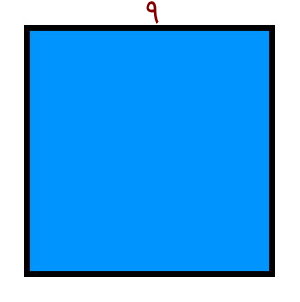
تمام ضلعهای مربع با یکدیگر برابر هستند. به همین دلیل، طول ضلع را کنار تمام ضلعها یادداشت میکنیم.
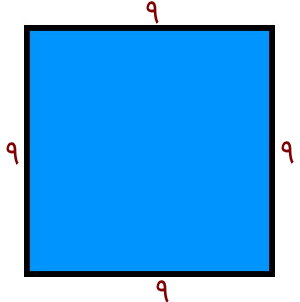
محیط، از جمع طول ضلعهای شکل هندسی به دست میآید. بنابراین:
9 + 9 + 9 + 9 = محیط
36 = محیط
محیط مربعی به ضلع ۹ برابر 36 است. در صورت استفاده از رابطه محیط مربع با ضلع، داریم:
ضلع مربع 4 = محیط مربع
9 4 = محیط
36 = محیط
همانطور که مشاهده میکنید، نتیجه محاسبه محیط مربع در دو حالت برابر شد. روش اول (جمع تمام ضلعها)، بیشتر در واقعیت مورد استفاده قرار میگیرد. به عنوان مثال، اگر از مربعی بودن شکل یک محدوده مطمئن نیستید، میتوانید تمام ضلعهای آن را اندازهگیری کنید و سپس محیط آن را به دست بیاورید.
مثال دوم: محاسبه محیط باغچه
فردی در حیاط خانه خود، یک باغچه مربعی شکل ساخته است. این فرد قصد دارد در اطراف باغچه خود، یک ردیف گل سفید رنگ بکارد. اگر طول یکی از ضلعهای باغچه برابر 3 متر باشد، محیط کاشت گلهای سفید چند متر خواهد بود؟

به منظور حل مسئله، ابتدا شکل ساده شده باغچه بالا را رسم میکنیم.
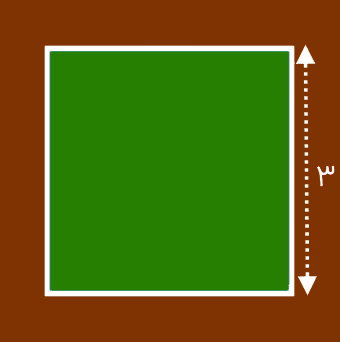
در صورت کاشت گلهای سفید در اطراف باغچه، محیط کاشت برابر با محیط باغچه است. مطابق با رابطه محیط مربع، داریم:
ضلع مربع 4 = محیط مربع
- P: محیط باغچه
- a: ضلع باغچه
به این ترتیب:
ضلع باغچه 4 = محیط باغچه
3 4 = محیط باغچه
12 = محیط باغچه
در نتیجه، حدود 12 متر گل در اطراف باغچه کاشته میشود.
مثال سوم: تعیین نوار خطر مورد نیاز
بخش کوچکی از زمین یک محل عمومی تخریب شده است. برای جلوگیری از ورود افراد، باید نوار خطر در اطراف این بخش نصب شود. اگر طول محدوده، برابر 70 سانتیمتر و شکل محدوده نصب نوار، مربعی باشد، طول نوار مورد نیاز برای نصب چقدر خواهد بود؟

به منظور درک بهتر مسئله، شکل ساده شده آن را رسم میکنیم.
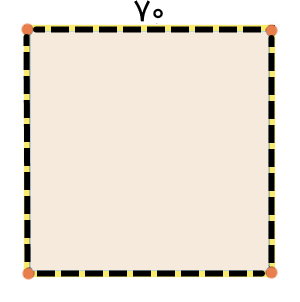
طول نوار مورد نیاز برای نصب در اطراف محدوده مشخص شده، برابر محیط محدوده است. به همین دلیل، برای محاسبه آن باید از رابطه محیط مربع استفاده کرد. مطابق این رابطه داریم:
ضلع محدوده 4 = محیط محدوده خطر
70 4 = محیط محدوده خطر
280 = محیط محدوده خطر
در نتیجه، برای مشخص کردن محدوده، به حداقل 280 سانتیمتر یا 2.8 متر نوار خطر نیاز خواهد بود.
مثال چهارم: محاسبه مجموع محیطها
مربعهای تو در توی زیر را در نظر بگیرید. مجموع محیطهای این سه مربع چقدر است؟
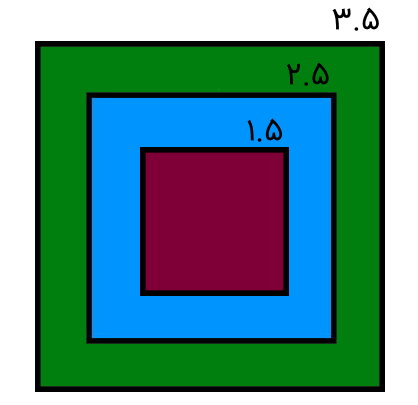
برای محاسبه مجموع محیط مربعهای بالا، مربع بزرگ تا کوچک را به ترتیب، با عنوان مربع 1، مربع 2 و مربع 3 در نظر میگیریم. اطلاعات مسئله را به شکل زیر یادداشت میکنیم:
- ضلع مربع 1 برابر 3.5
- ضلع مربع 2 برابر 2.5
- ضلع مربع 3 برابر 1.5
محیط مربع 1 برابر است با:
ضلع مربع 1 4 = محیط مربع 1
3.5 4 = محیط مربع 1
14 = محیط مربع 1
محیط مربع 2 به صورت زیر محاسبه میشود:
ضلع مربع 2 4 = محیط مربع 2
2.5 4 = محیط مربع 2
10 = محیط مربع 2
محیط مربع 3 نیز از رابطه زیر به دست میآید:
ضلع مربع 3 4 = محیط مربع 3
1.5 4 = محیط مربع 3
6 = محیط مربع 3
مجموع محیطها برابر است با:
محیط مربع 3 + محیط مربع 2 + محیط مربع 1 = مجموع محیطها
6 + 10 + 14 = مجموع محیطها
20 = مجموع محیطها
مجموع محیط مربعهای تو در تو در این مثال برابر 20 است.
مثال پنجم: محاسبه محیط از روی مساحت
محیط مربعی به مساحت 225 سانتیمتر مربع چقدر است؟
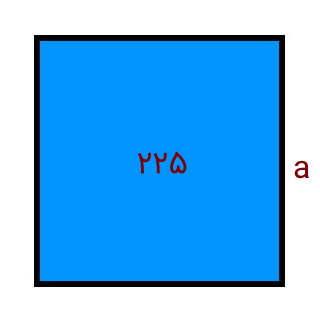
مساحت مربع برابر طول یک ضلع ضربدر خودش یا یک ضلع به توان دو است. فرمول مساحت مربع به صورت زیر نوشته میشود:
- A: مساحت
- a: ضلع مربع
عدد مساحت را درون رابطه بالا جایگذاری کرده و رابطه را بر حسب ضلع (a) حل میکنیم:
طول ضلع مربع برابر 15 سانتیمتر است. با قرار دادن این عدد در فرمول محیط مربع، جواب نهایی مسئله به دست میآید:
15 4 = محیط مربع
60 = محیط مربع
محیط مربعی به مساحت 225 سانتیمتر مربع برابر 60 سانتیمتر است. اگر به یادگیری بیشتر راجع به مساحت مربع و روشهای محاسبه آن علاقهمند هستید، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
- فرمول مساحت مربع چیست؟ — به زبان ساده + حل تمرین و مثال
- مساحت مربع به صورت جبری — فرمولهای ریاضی + حل تمرین و مثال
- مساحت مربع داخل دایره چگونه بدست میآید؟ — به زبان ساده + تمرین و مثال
- مساحت مربع با قطر چگونه بدست میآید؟ – به زبان ساده + حل تمرین و مثال
مثال ششم: مقایسه مربع و مستطیل
تصویر زیر، مربعی با ضلع ۵ و مستطیلی با طول ۶ و عرض ۴ را نمایش میدهد. محیط کدام شکل بیشتر است؟
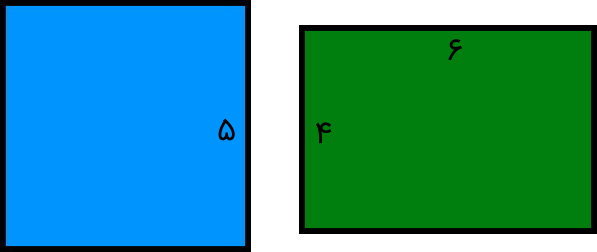
محیط مربع از رابطه زیر به دست میآید:
- P: محیط
- a: ضلع مربع
ضلع مربع 4 = محیط مربع
5 4 = محیط مربع
20 = محیط مربع
برای تعیین محیط مستطیل میتوان از رابطه مخصوص آن یا جمع تمام ضلعها استفاده کرد. مطابق با رابطه کلی محیط مستطیل داریم:
- P: محیط
- l: طول مستطیل
- w: عرض مستطیل
(عرض مستطیل) 2 + (طول مستطیل) 2 = محیط مستطیل
(4) 2 + (6) 2 = محیط مستطیل
8 + 12 = محیط مستطیل
20 = محیط مستطیل
به این ترتیب، محیط مربعی به ضلع 5 با محیط مستطیلی به طول 6 و عرض 4 برابر است. البته در صورت مقایس مساحتها، متوجه خواهید شد که مساحت مربع با ضلع 5 از مساحت مستطیل با طول 6 و عرض 4 بیشتر است.
محاسبه محیط مربع با قطر
در بخشهای ابتدایی اشاره کردیم که فرمول محیط مربع با قطر به صورت زیر نوشته میشود:
- P: محیط
- d: قطر
در انتهای این بخش، نحوه اثبات رابطه بالا را با استفاده از قضیه فیثاغورس توضیح میدهیم.
مثال اول: محاسبه محیط با قطر
محیط مربعی با قطر را محاسبه کنید.
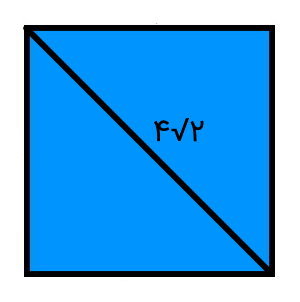
مطابق با فرمول محیط مربع با قطر برابر است با:
محیط مربع برابر 16 است.
مثال دوم: محاسبه محیط مربع محاط در دایره
تصویر زیر، دایرهای به شعاع و مربع محاطی درون این دایره را نمایش میدهد. محیط مربع را به دست بیاورید.
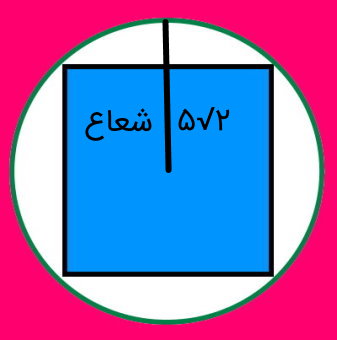
اگر برخی از قطرهای دایره بالا را رسم کنید، متوجه خواهید شد که قطر مربع محاط در دایره، برابر قطر دایره است.

به همین دلیل، میتوانیم رابطه بین شعاع دایره و قطر مربع محاط در آن را به صورت زیر بنویسیم:
شعاع دایره ۲ = قطر دایره = قطر مربع
۲ = قطر مربع
= قطر مربع
= قطر مربع
با دانستن مقدار قطر مربع، امکان استفاده از فرمول محیط مربع با قطر فراهم میشود. مطابق این فرمول، داریم:
در این مثال، محیط مربع محاط بر دایره برابر 40 است.
اثبات فرمول محیط مربع با قطر
به منظور اثبات فرمول محیط مربع با قطر، تصویر زیر را در نظر بگیرید. در این تصویر، یکی از قطرهای مربع رسم شده است.
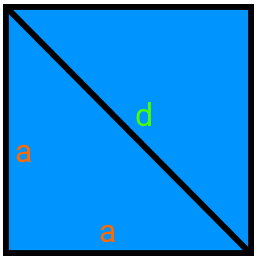
مطابق با قضیه فیثاغورس در مثلث قائم الزاویه، داریم:
- a: یکی از ساقهای مثلث قائم الزاویه
- b: ساق دیگر مثلث قائم الزاویه
- c: وتر مثلث قائم الزاویه
ساقهای مثلث قائم الزاویه در مربع بالا برابر a بوده و وتر مثلث برابر d است. به این ترتیب، رابطه بالا، به صورت زیر بازنویسی میشود:
طی مراحل بالا، طول ضلع مربع بر حسب طول قطر آن به دست میآید. با قرار دادن رابطه بالا در فرمول کلی میتوان محیط مربع را حساب کرد. با این وجود، به منظور سادهسازی، رابطه بالا را به صورت زیر مینویسیم:
فرمول محیط مربع برابر است با:
فرمول محاسبه مستقیم محیط مربع با قطر به دست میآید.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مربع — تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مربع چیست ؟ — تعریف و مفاهیم به زبان ساده (+ فیلم آموزش رایگان)
- قطر مربع چیست و چگونه بدست می آید ؟ — به زبان ساده + حل تمرین و مثال
- چگونه محیط مربع را حساب کنیم؟ + فیلم آموزشی و حل تمرین(همین مطلب)
- مساحت مربع چگونه بدست می آید؟ + فیلم آموزشی و حل تمرین و مثال
- طول ضلع مربع به محیط آن چیست؟ + حل تمرین و مثال
- فرمول محیط مربع چیست ؟ — به زبان ساده + حل تمرین و مثال
- فرمول مساحت مربع چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط مربع به صورت جبری — فرمول های ریاضی + حل تمرین و مثال
- مساحت مربع به صورت جبری — فرمول های ریاضی + حل تمرین و مثال
- مساحت مربع داخل دایره چگونه بدست می آید ؟ — به زبان ساده + تمرین و مثال
- مساحت مربع با قطر چگونه بدست می آید ؟ – به زبان ساده + حل تمرین و مثال













Nice