چگونه مساحت مثلث را حساب کنیم؟ + فیلم آموزشی و تمرین با جواب

مساحت مثلث برابر با قاعده ضربدر ارتفاع تقسیم بر دو است. البته روشهای مختلفی برای اندازهگیری مساحت مثلثها وجود دارند. علاوه بر این، تمام مثلثها شبیه به یکدیگر نبوده و در بسیاری از موارد، قاعده و ارتفاع مثلث، مشخص نیستند. به همین دلیل، روش مناسب برای محاسبه مساحت انواع مثلثها در مسائل مختلف، متفاوت خواهد بود. در این آموزش از مجله فرادرس چندین روش برای اندازهگیری مساحت مثلثها را توضیح میدهیم. پس از ارائه مفاهیم اولیه، علاوه بر فرمولهای مخصوص دانش آموزان پایه ابتدایی، به معرفی روشهای پیشرفتهتر برای دانش آموزان پایه متوسطه نیز میپردازیم.
فیلم آموزشی مساحت مثلث
فرمول مساحت مثلث چیست ؟
سادهترین و شناخته شدهترین فرمول مساحت مثلث، «قاعده ضرب در ارتفاع تقسیم بر 2» است.
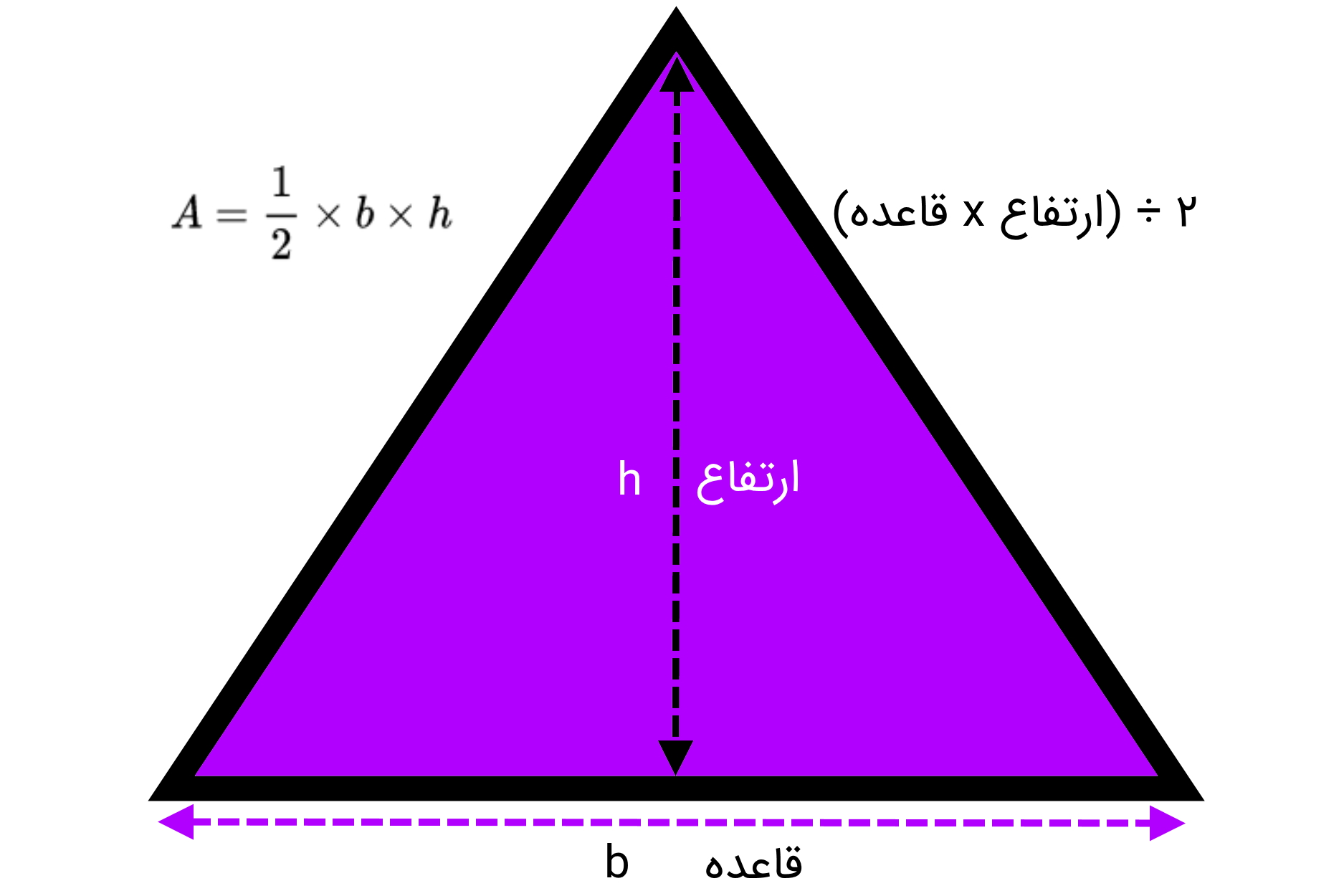
برای محاسبه مساحت مثلثها مطابق با این فرمول، ابتدا باید قاعده و ارتفاع آن را پیدا کرد. مثلث، یکی از انواع چندضلعیها است که از سه ضلع و سه راس تشکیل میشود. شکل زیر، یکی از انواع مثلث را نمایش میدهد. راسهای این مثلث با حروف (م، و، ن) و ضلعهای آن با اعداد (1، 2، 3) مشخص شدهاند.
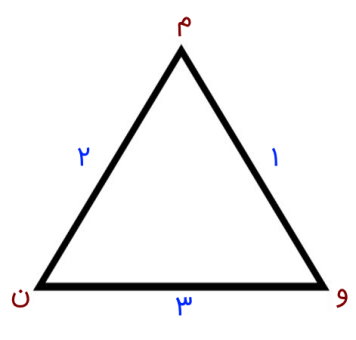
راس (م) و ضلع (3) در مثلث بالا را در نظر بگیرید. از راس (م)، یک پاره خط عمود بر ضلع (3) رسم میکنیم. طول این پاره خط، یکی از ارتفاعهای مثلث و طول ضلع (۳)، قاعده نظیر این ارتفاع است. برای آشنایی بیشتر با پارهخط در مجله فرادرس میتوانید مطلب «پاره خط ، خط و نیم خط — به زبان ساده» را مطالعه کنید.
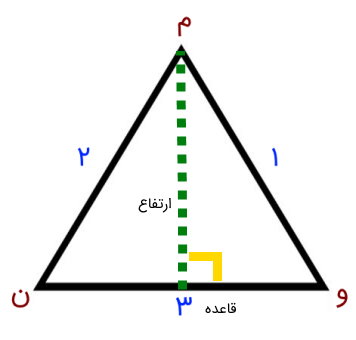
مثلث، دارای سه قاعده و سه ارتفاع است. تصویر زیر، ارتفاع و قاعدههای یک مثلث متوازی الاضلاع را نمایش میدهد.
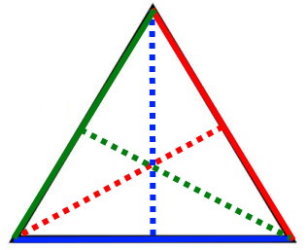
با دانستن طول یکی از ارتفاعها و طول قاعده نظیر در هر مثلث، میتوانید مساحت آن را مطابق با فرمول زیر محاسبه کنید:
۲ ÷ (ارتفاع قاعده) = مساحت مثلث
مثال محاسبه مساحت مثلث دلخواه
تصویر زیر را در نظر بگیرید. این تصویر، سه آهنربا را روی یک دفترچه یادداشت نمایش میدهد.

اگر مرکز آهنرباها را به هم وصل کنیم، یک مثلث به وجود میآید.

میخواهیم مساححت مثلث بالا را حساب کنیم. برای این کار، به اندازه یکی از قاعدهها و یکی از ارتفاعهای مثلث نیاز داریم.

با استفاده از خطکش، طول ضلعها و یکی از ارتفاعهای مثلث را اندازهگیری کردیم. این اندازهها بر حسب میلیمتر هستند. میدانیم که مساحت مثلث، یکدوم حاصلضرب ارتفاع در قاعده است. در تصویر بالا، ارتفاع نظیر قاعده ۷۵ میلیمتری برابر با ۵۸ میلیمتر است. بنابراین، داریم:
۲ ÷ (ارتفاع × قاعده) = مساحت مثلث
۲ ÷ (۵۸ × ۷۵) = مساحت مثلث
۲ ÷ ۴۳۵۰ = مساحت مثلث
۲۱۷۵ = مساحت مثلث
در نتیجه، مساحت مثلث برابر با ۲۱۷۵ میلیمتر مربع است.
علامت ریاضی مساحت مثلث چیست؟
در ریاضیات، مساحت مثلث و دیگر اشکال هندسی با حرف انگلیسی A یا a نمایش داده میشود. این حرف، ابتدای کلمه انگلیسی «Area» به معنای «مساحت» است. حرف انگلیسی H یا h نشان دهنده کلمه «ارتفاع» (Height) و حرف انگلیسی B یا b نیز بیانگر کلمه «قاعده» (Base) است.
فرمول ریاضی مساحت مثلث چیست؟
با توجه به علامتهای ریاضی مساحت، ارتفاع و قاعده، فرمول ریاضی مساحت مثلث به صورت زیر نوشته میشود:
- A: مساحت
- b: یکی از قاعدههای مثلث
- h: ارتفاع نظیر قاعده b
واحد مساحت مثلث چیست؟
نحوه بیان واحد یا یکای مساحت، به سیستم اندازهگیری و واحد اندازهگیری ابعاد بستگی دارد. در سیستم بینالمللی، بیان این واحد به صورت میلیمتر مربع، سانتیمتر مربع، متر مربع و غیره انجام میگیرد. به عنوان مثال، در صورتی که اضلاع مثلث به متر بیان شده باشند، نتیجه محاسبه سطح مثلثها به متر مربع بیان میشود. اگر اضلاع مثلث با یک واحد مشخص بیان شده باشند و بخواهید سطح مثلثها را با یک واحد دیگر محاسبه کنید، نیاز به تبدیل واحد خواهید داشت.
رابطه بین مساحت مثلث و دیگر اشکال هندسی چگونه است؟
اگر به اشکال چندضلعی نظیر مربع، مستطیل، لوزی، متوازی الاضلاع و غیره دقت کنید، متوجه خواهید شد که این شکلها، از چندین مثلث تشکیل میشوند. به عنوان مثال، تصویر زیر یک مستطیل را نمایش میدهد.

اگر از راس (الف)، پاره خطی را به سمت راس (ب) رسم کنیم، شکل زیر به وجود میآید.
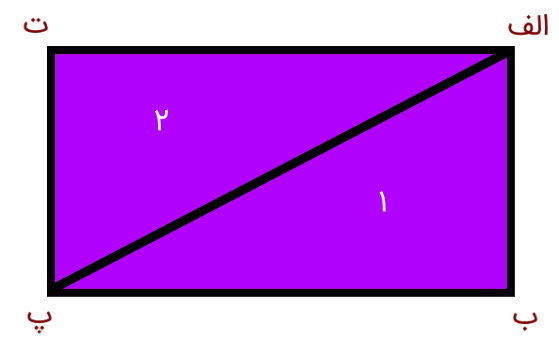
مطابق با تصویر بالا مشاهده میکنید که مستطیل (الف ب پ ت)، میتواند به دو مثلث (الف ب ت) و (ب پ ت) تقسیم شود. البته در صورت رسم یک پاره خط دیگر از راس (ت) به راس (ب)، مستطیل (الف ب پ ت) به چهار مثلث تقسیم خواهد شد.
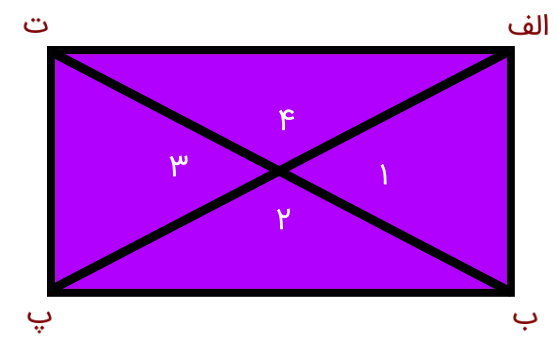
بر اساس تصاویر بالا، نتیجه میگیریم که مساحت چندضلعیها، مجموعهای از مساحت مثلثهای تشکیل دهنده آنها است.
کاربرد مساحت مثلث چیست؟
مساحت مثلث، در اندازهگیری محدودههای مثلثی شکل و حتی چندضلعی کاربرد دارد. در دنیای واقعی، اجسام دارای شکلهای مختلفی هستند. به عنوان مثال، ساختمانها بر روی محدودههایی به شکل مستطیل، مربع، مثلث و غیره ساخته میشوند. به منظور تعیین محدوده ساخت این ساختمانها، باید مساحت آنها را تعیین کرد. در مثالی دیگر، لوازم خانگی مانند میزها نیز میتوانند به شکل مثلث ساخته شوند. برای تعیین ابعاد روکش مورد نیاز برای پوشاندن سطح این لوازم، باید اندازه سطح مثلث تشکیل دهنده آنها را محاسبه کرد.

بسیاری از اجسام نظیر سقفهای شیروانی، خرپاها، بادبانها، راهپلهها و برخی از وسایل شکل مثلثی دارند. به علاوه، شکلهایی نظیر مربع، متوازی الاضلاع، لوزی، مستطیل، ذوزنقه و دیگر شکلهای چندضلعی را میتوان به مجموعهای از دو یا چند مثلث تبدل کرد و مساحت آنها را به دست آورد. به پیدا کردن مساحت چندضلعیها با تبدیل آنها به مثلثهای کوچکتر، مساحی میگویند.
حل مسائل مساحت مثلث
در بخش قبلی، با رابطه کلی تعیین مساحت مثلثها و مفاهیم ابتدایی مربوط به آنها آشنا شدید. در این بخش، برای یادگیری بهتر نحوه انجام محاسبات در حالتهای مختلف، به تشریح چند مثال ساده میپردازیم.
مثال اول: محاسبه مساحت مثلث بدون شکل
مساحت مثلثی با قاعده 8 سانتیمتر و ارتفاع 7 سانتیمتر چقدر است؟
به دلیل مشخص بودن قاعده و ارتفاع نظیر آن، امکان استفاده از رابطه کلی مساحت مثلثها وجود دارد. اطلاعات مثال عبارت هستند از:
- h = ارتفاع = 8 سانتیمتر
- b = قاعده = 7 سانتیمتر
رابطه کلی مساحت مثلثها عبارت است از:
۲ ÷ (ارتفاع قاعده) = مساحت مثلث
۲ ÷ (78) = مساحت مثلث
۲ ÷ (56) = مساحت مثلث
28 = مساحت مثلث
مساحت به دست آمده، 28 سانتیمتر مربع است. در مثال بالا، از هیچ شکلی برای نمایش مشخصات مثلث استفاده نکردیم. از این مثال میتوان نتیجه گرفت که مساحت هر مثلثی با ارتفاع 8 سانتیمتر و قاعده نظیر 7 سانتیمتر، برابر با 28 سانتیمتر خواهد بود.
مثال دوم: محاسبه مساحت مثلث از روی شکل
مساحت مثلث نمایش داده شده در شکل زیر چقدر است؟
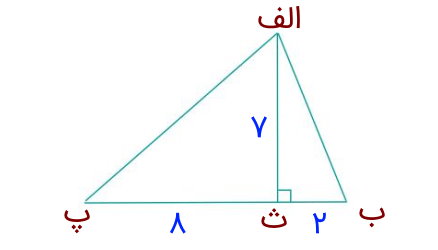
با توجه تصویر بالا، ارتفاع (الف ث) برابر 7 سانتیمتر است. قاعده نظیر این ارتفاع، یعنی ضلع (ب پ)، از پاره خط (ب ث) با طول 2 سانتیمتر و پاره خط (پ ث) با طول 8 سانتیمتر تشکیل میشود. به همین دلیل، برای تعیین طول قاعده (ب پ)، باید طول پاره خطهای (ب ث) و (پ ث) را با هم جمع کنیم. به این ترتیب داریم:
۲ ÷ (ارتفاع قاعده) = مساحت مثلث
۲ ÷ ((7) (8+2)) = مساحت مثلث الف ب پ
۲ ÷ (7 10) = مساحت مثلث الف ب پ
۲ ÷ (70) = مساحت مثلث الف ب پ
35 = مساحت مثلث الف ب پ
سطح داخل مثلث (الف ب پ) برابر با 35 سانتیمتر مربع است.
مثال سوم: مساحت مثلث با زاویه باز
تصویر زیر، یک مثلث با زاویه باز را نمایش میدهد. با توجه به اطلاعات نمایش داده شده، مساحت مثلث چقدر است؟
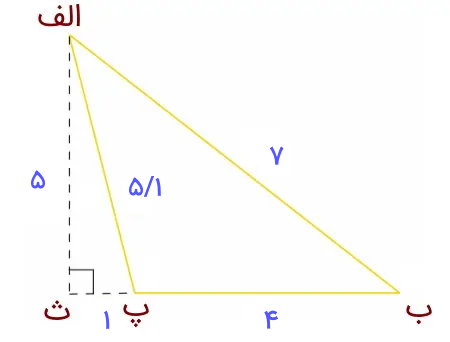
راس (پ) در مثلث (الف ب پ)، دارای زاویه بیشتر از 90 درجه (زاویه باز) است. به همین دلیل، برای مشخص کردن ارتفاع نظیر ضلع (ب پ)، امتداد این ضلع تا نقطه (ث) رسم شده است. با توجه به اطلاعات مسئله داریم:
۲ ÷ (ارتفاع قاعده) = مساحت مثلث
۲ ÷ (۴ ۵) = مساحت مثلث الف ب پ
۲ ÷ (۲۰) = مساحت مثلث الف ب پ
۱۰ = مساحت مثلث الف ب پ
سطح داخل مثلث (الف ب پ) برابر با ۱۰ سانتیمتر مربع است. برای محاسبه اندازه سطح مثلثهای دارای زاویه باز، طول ضلع یا قاعده را با بخش امتداد یافته جمع نکنید. در مثال بالا، طول پاره خط (پ ث) با مقدار 1.5 سانتیمتر، هیچ تاثیری در محاسبات ندارد.
مثال چهارم: مساحت مثلث با زاویه راست
تصویر زیر، یک مثلث با زاویه راست را نمایش میدهد. مساحت این مثلث چقدر است؟
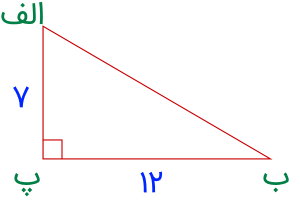
در مثلث بالا، راس (پ) دارای زاویه 90 درجه است. این زاویه از اتصال ضلع (ب پ) با طول 12 سانتیمتر و ضلع (الف پ) با طول 7 سانتیمتر به یکدیگر تشکیل میشود. بنابراین، این دو ضلع، قاعده و ارتفاع نظیر یکدیگر هستند. به این ترتیب داریم:
۲ ÷ (ارتفاع قاعده) = مساحت مثلث
۲ ÷ (7 12) = مساحت مثلث الف ب پ
۲ ÷ (84) = مساحت مثلث الف ب پ
42 = مساحت مثلث الف ب پ
سطح داخل مثلث (الف ب پ) برابر با 42 سانتیمتر مربع است. توجه داشته باشید که در این مثال، هر دو ضلع (ب پ) و (الف پ) را میتوان به عنوان قاعده و ارتفاع در نظر گرفت.
مثال پنجم: تعیین ضلع مثلث از روی مساحت آن
تصویر زیر، مثلثی با مساحت 20 سانتیمتر مربع را نمایش میدهد. طول ضلع (ب پ) چقدر است؟

با توجه به اطلاعات نمایش داده شده در تصویر بالا، پاره خط (الف ث)، ارتفاع نظیر ضلع (ب پ) است. به این ترتیب داریم:
۲ ÷ (ارتفاع قاعده) = مساحت مثلث
۲ ÷ (پاره خط الف ث ضلع ب پ) = مساحت مثلث الف ب پ
۲ ÷ (5 ضلع ب پ) = 20
با ضرب متقاطع (طرفین و وسطین)، رابطه بالا به شکل زیر در میآید:
5 ضلع ب پ = 40
ضلع ب پ = 5 ÷ 40
8 = ضلع ب پ
به این ترتیب، طول ضلع (ب پ) برابر با 8 سانتیمتر است.
مثال ششم: تعیین مساحت قسمت رنگی مثلث
تصویر زیر، مثلثی با یک مربع در داخلش را نمایش میدهد. اگر طول یک ضلع مربع برابر 5 سانتیمتر باشد، مساحت بخش رنگی مثلث چقدر است؟
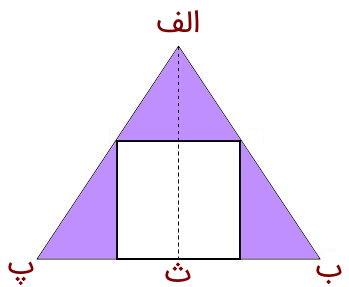
از آنجایی که تمام مربع در داخل مثلث قرار دارد، مساحت بخش رنگی، از تعیین اختلاف مساحت مثلث با مساحت مربع به دست میآید. به این ترتیب داریم:
مساحت مربع - مساحت مثلث = مساحت ناحیه رنگی
مساحت مربع برابر یک ضلع ضربدر خودش است. بنابراین:
(5 5) = مساحت مربع
25 = مساحت مربع
ارتفاع مثلث (پاره خط الف ث) برابر 9 سانتیمتر و قاعده نظیر آن (ضلع ب پ) برابر 10 سانتیمتر است. بر اساس این اطلاعات، خواهیم داشت:
۲ ÷ (ارتفاع قاعده) = مساحت مثلث
۲ ÷ (پاره خط الف ث ضلع ب پ) = مساحت مثلث الف ب پ
۲ ÷ (9 10) = مساحت مثلث الف ب پ
۲ ÷ (90) = مساحت مثلث الف ب پ
45 = مساحت مثلث الف ب پ
مساحت مربع، برابر با 25 سانتیمتر مربع و مساحت مثلث، برابر با 45 سانتیمتر مربع شد. در نتیجه، مساحت ناحیه رنگی برابر از رابطه زیر به دست میآید:
25 - 45 = مساحت ناحیه رنگی
20 = مساحت ناحیه رنگی
مساحت ناحیه رنگی برابر 20 سانتیمتر مربع است.
روش های محاسبه مساحت مثلث کدام هستند؟
از شناخته شدهترین روشهای تعیین سطح مثلث میتوان به روش قاعده و ارتفاع، روش هرون (طول سه ضلع) و روش مثلثاتی (ضلع و زاویه) اشاره کرد. البته امکان اندازهگیری مساحت انواع مثلثها، با استفاده از تشابه، دترمینان و ضرب خارجی نیز وجود دارد. به طور کلی، روش محاسبه سطح مثلث، بر اساس اطلاعات در دسترس انجام میگیرد. جدول زیر، انواع روشهای محاسبه سطح مثلثها را نمایش میدهد.
| اطلاعات در دسترس | روش محاسبه مساحت |
| قاعده و ارتفاع نظیر | قاعده ضربدر ارتفاع تقسیم بر دو |
| سه ضلع | فرمول هرون |
| دو ضلع و زاویه بین، دو زاویه و ضلع بین، دو ضلع و زاویه غیر بین، دو زاویه و ضلع غیر بین | مثلثات |
روش قاعده و ارتفاع، پایهایترین روش برای محاسبه مساحت انواع مثلثها است. در صورتی که قاعده و ارتفاع نظیر آن در یک مثلث مشخص باشند، مساحت آن از ضرب قاعده در ارتفاع تقسیم بر دو به دست میآید. در بخش قبلی، نحوه محاسبه سطح مثلثها توسط این روش را به همراه چندین مثال توضیح دادیم. در بخشهای بعدی، به معرفی انواع دیگر روشهای اندازهگیری سطح مثلثها خواهیم پرداخت.
مساحت انواع مثلثها
مثلثها انواع مختلفی دارند که از شناخته شدهترین آنها میتوان به مثلث قائم الزاویه، مثلث متساوی الساقین، مثلث متساوی الاضلاع، مثلث مختلف الاضلاع و مثلث منفرجه اشاره کرد. در این بخش، روشهای محاسبه مساحت این اشکال را بررسی میکنیم.
مساحت مثلث قائم الزاویه چگونه محاسبه میشود؟
سطح مثلث قائم الزاویه، از حاصلضرب ضرب ساقها تقسیم بر دو به دست میآید. مثلث قائم الزاویه، مثلثی با یک زاویه 90 درجه است. در کتابها و منابع آموزشی، زاویه قائم این مثلث، با یک مربع کوچک (□) نشان داده میشود. البته توجه داشته باشید که جمع زوایای داخلی مثلث برابر با 180 درجه است. به این ترتیب، اگر مجموع دو زاویه مثلث برابر با 90 درجه بود، زاویه سوم، قائمه است (حتی اگر علامت مربع نمایش داده نشود). تصویر زیر، نمونهای از یک مثلث قائم الزاویه است.
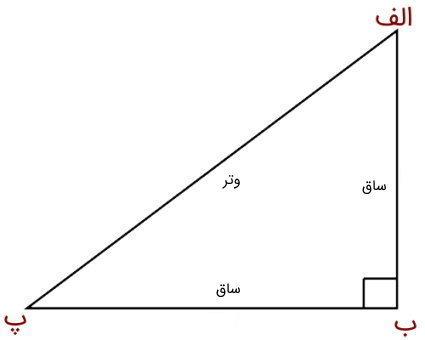
به اضلاع متصل به زاویه قائمه، ساقهای مثلث میگویند. در تصویر بالا، ضلع (الف ب) و ضلع (ب پ)، دو ساق مثلث هستند. ضلع (الف پ)، با عنوان وتر شناخته میشود. نکته جالب در مورد مثلثهای قائم الزاویه این است که ساقها، ارتفاع و قاعده نظیر یکدیگر به حساب میآیند. از اینرو، دانستن مقدار آنها برای تعیین مساحت مثلث قائم الزاویه کفایت میکند. به این ترتیب داریم:
۲ ÷ (ساق دوم ساق اول) = مساحت مثلث قائم الزاویه
نکته: قضیه فیثاغورس در این مثلثهای متساوی الساقین، از اهمیت بالایی برای محاسبه مساحت چندضلعیهای دیگر و مثلث متساوی الاضلاع برخوردار است.
مثال: تعیین مساحت مثلث قائمه
مثلث (آ ب پ) را در نظر بگیرید. اضلاع (الف ب) و (ب پ)، ساقهای این مثلث هستند که طول آنها به ترتیب برابر با ۱۲ و ۷ واحد است. میخواهیم مساحت این مثلث را به دست بیاوریم.
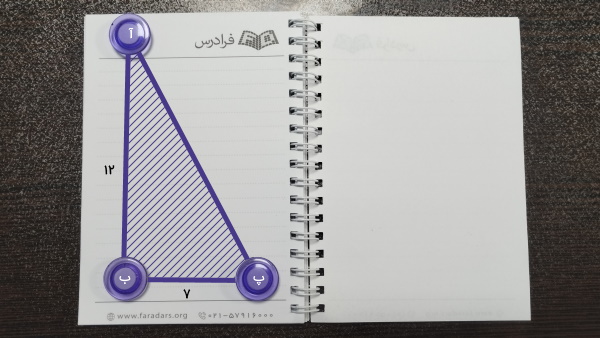
فرمول کلی محاسبه مساحت مثلثهای قائم برابر است با:
۲ ÷ (ساق دوم ساق اول) = مساحت مثلث قائم الزاویه
از آنجایی که اضلاع (آ ب) و (ب پ)، ساقهای مثلث (آ ب پ) هستند، خواهیم داشت:
۲ ÷ (ارتفاع قاعده) = مساحت مثلث
۲ ÷ (ضلع ب پ ضلع آ ب) = مساحت مثلث قائم الزاویه (آ ب پ)
۲ ÷ (۱۲x۷) = مساحت مثلث قائم الزاویه (آ ب پ)
۲ ÷ (۸۴) = مساحت مثلث قائم الزاویه (آ ب پ)
۴۲ = مساحت مثلث قائم الزاویه (آ ب پ)
به این ترتیب، مساحت مثلث برابر با ۴۲ با واحد طول مربع است. توجه داشته باشید که در تمام مسائل، طول ساقهای مثلث قائم الزاویه را مشخص نمیکنند. در برخی از موارد، اندازه سطح مثلث قائم الزاویه باید با توجه به طول وتر و ارتفاع نظیر آن یا طول یکی از اضلاع و زاویه مجاور آن محاسبه شود. در بخش مثالها، به توضیح نحوه حل این گونه مسائل نیز خواهیم پرداخت.
مساحت مثلث متساوی الساقین
سطح مثلث متساوی الساقین، از حاصلضرب قاعده در ارتفاع تقسیم بر دو به دست میآید. مثلث متساوی الساقین، مثلثی با دو ضلع برابر است. در کتابها و منابع آموزشی، برابر بودن ضلعهای مثلث توسط خطوط کوچک عمود بر اضلاع (مانند /، یا |) نمایش داده میشود. البته اگر دو زاویه مثلث با هم برابر باشند، اضلاع مقابل آن دو زاویه نیز با هم برابر خواهند بود (حتی اگر علامت خطوط کوچک نمایش داده نشود). تصویر زیر، نمونهای از یک مثلث متساوی الساقین است.
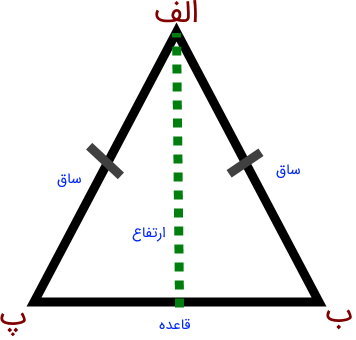
به ضلعهای برابر مثلث متساوی الساقین، ساق و به ضلع سوم آن، قاعده میگویند. در صورت قائمه بودن زاویه بین ساقها، یک مثلث قائم الزاویه متساوی الساقین تشکیل میشود. در پایه ابتدایی، روش محاسبه مساحت مثلثهای متساوی الساقین، تفاوتی با حالت کلی ندارد.
مساحت مثلث متساوی الاضلاع
مثلث متساوی الاضلاع، مثلثی با سه ضلع برابر است. در کتابها و منابع آموزشی، متساوی الاضلاع بودن مثلث، با گذاشت علامت بر روی تمام ضلعها نمایش داده میشود. توجه داشته باشید که در صورت برابر بودن تمام اضلاع یک مثلث، تمام زوایای داخلی آن نیز برابر خواهند بود. از اینرو، اگر دو زاویه مثلث برابر با 60 درجه باشد، آن مثلث، متساوی الاضلاع است. تصویر زیر، یک مثلث متساوی الاضلاع را نمایش میدهد.
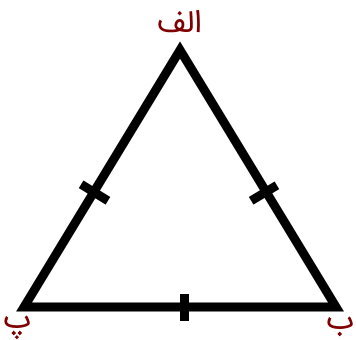
مثلث متساوی الاضلاع، یکی از انواع مثلثهای متساوی الساقین است. با این تفاوت که در این مثلثها، تمام اضلاع (قاعدهها)، تمام زوایا و تمام ارتفاعها (به صورت جداگانه) با یکدیگر برابر هستند. این ویژگی، یک روش به روشهای محاسبه سطح مثلث متساوی الاضلاع اضافه میکند. به دلیل اضلاع برابر، فرمول محاسبه اندازه سطح مثلثهای متساوی الاضلاع را میتوان به صورت زیر بازنویسی کرد:
- A: مساحت
- a: طول یکی از ضلعهای مثلث
اثبات رابطه بالا توسط قضیه فیثاغورس و تقسیم مثلث متساوی الاضلاع به دو مثلث متساوی الساقین انجام میگیرد.
مثال: تعیین سطح مثلث با سه زاویه مساوی
مثلث رسم شده در دفترچه یادداشت زیر، دارای سه زاویه ۶۰ درجه و سه ضلع ۸ سانتیمتری است. میخواهیم ارتفاع این مثلث را محاسبه کنیم.

اگر تمام زوایای یک مثلث برابر با ۶۰ درجه باشند، آن مثلث، متساوی الاضلاع خواهد بود. مطابق با فرمول مخصوص مساحت مثلث متساوی الاضلاع، داریم:
مساحت مثلث، برابر با ۲۷/۶۸ سانتیمتر مربع است. اکنون، برای پیدا کردن ارتفاع، از رابطه کلی اندازه سطح مثلثها استفاده میکنیم:
- A: مساحت (برابر ۲۷/۶۸)
- b: قاعده (طول ضلع مثلث برابر ۸)
- h: ارتفاع
مقادیر موجود را در رابطه بالا قرار میدهیم:
با استفاده طرفین و وسطین، مقدار ارتفاع را به دست میآوریم:
به این ترتیب، ارتفاع مثلث برابر با ۶/۹۲ سانتیمتر است.
سطح مثلث منفرجه
مثلث منفرجه، مثلثی با یک زاویه بیشتر از 90 درجه است. در تصویر زیر نمونهای از یک مثلث منفرجه را مشاهده میکنید. اگر بخواهیم محاسبه مساحت این مثلث را بر اساس قاعده (ب پ) انجام دهیم، باید ارتفاع نظیر آن را از راس (الف) رسم کنیم. به دلیل منفرجه بودن راس (ب)، امکان رسم پاره خط عمود بر ضلع (ب پ) وجود ندارد. به همین دلیل، این ضلع را امتداد میدهیم. سپس، یک پاره خط را از راس (الف)، عمود بر امتداد ضلع (ب پ) رسم میکنیم. فاصله راس (الف) تا محل برخورد در نقطه (ث)، ارتفاع نظیر قاعده (ب پ) است.
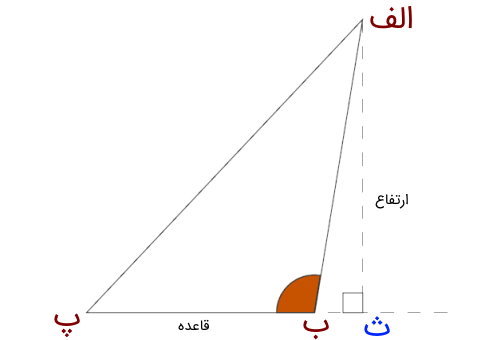
فرمول مساحت مثلث منفرجه نمایش داده شده در تصویر بالا برابر است با:
۲ ÷ (ارتفاع قاعده) = مساحت مثلث
۲ ÷ (پاره خط الف ث ضلع ب پ) = مساحت مثلث منفرجه (الف ب پ)
به منظور رسم ارتفاع قاعده (الف ب) نیز باید ضلع آن را امتداد داد. به طور کلی، در مثلثهای منفرجه، دو ارتفاع نظیر اضلاع زاویه منفرجه، در خارج از مثلث قرار میگیرند. البته در صورت مشخص بودن مقادیر ارتفاع، این ویژگی، تاثیری بر روی نحوه محاسبات نخواهد داشت.
سطح مثلث مختلف الاضلاع
مثلث مختلف الاضلاع، مثلثی است که هیچ یک از اضلاع آن با یکدیگر برابر نیستند. این مثلث میتواند از نوع قائم الزاویه، منفرجه یا حاده باشد. محاسبه سطح مثلثهای مختلف الاضلاع، توسط روشهای کلی نظیر قاعده ضربدر ارتفاع تقسیم بر دو، روش هرون، روش مثلثاتی و غیره انجام میگیرد. مسئله مهم در انتخاب روش تعیین مساحت این مثلثها، مانند مثلثهای دیگر، اطلاعات در دسترس (طول، زاویه و مختصات) است.
مساحت مثلث به روش هرون
محاسبه مساحت مثلث با داشتن سه ضلع آن (حالت ض ض ض) امکانپذیر است. در صورت مشخص بودن طول تمام اضلاع مثلث، از فرمول هرون برای محاسبه مساحت استفاده میشود.
قدمت این فرمول به حدود 2000 سال پیش باز میگردد. برای به کارگیری این فرمول، باید با مفهوم محیط مثلث و رادیکال آشنا باشید.
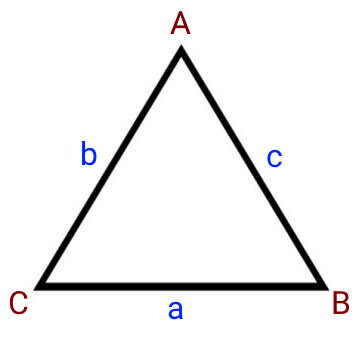
تصویر بالا، مثلث (الف ب پ) و طول ضلعهای آن را به صورت پارامتری (استفاده از حروف) نمایش میدهد. فرم ریاضی فرمول هرون برای محاسبه مساحت این مثلث به صورت زیر است:
در رابطه بالا داریم:
- A: مساحت (الف ب پ)
- s: نصف محیط مثلث
- a: طول ضلع (الف ب)
- b: طول ضلع (ب پ)
- c: طول ضلع (الف پ)
پارامتر s در رابطه بالا از رابطه زیر محاسبه میشود:
مثال: تعیین سطح مثلث با سه ضلع
مثلث زیر را در نظر بگیرید. اگر طول تمام ضلعهای این مثلث برابر 5 سانتیمتر باشد، مساحت آن و طول ارتفاع نظیر ضلع (ب پ) چقدر خواهد بود؟
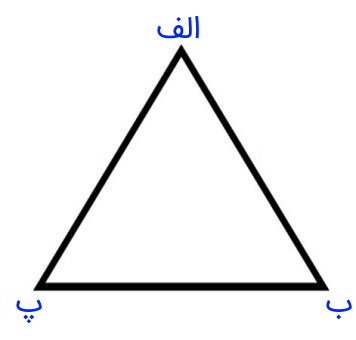
به دلیل مشخص بودن طول تمام ضلعهای مثلث، میتوانیم از فرمول هرون برای محاسبه مساحت استفاده کنیم. بر اساس این فرمول، داریم:
نصف محیط مثلث برابر است با:
مقادیر مسئله را در رابطه بالا جایگذاری میکنیم:
نصف محیط مثلث (الف ب پ) برابر 7.5 سانتیمتر است. با جایگذاری این مقدار و مقادیر ضلعهای مثلث در فرمول هرون، خواهیم داشت:
مطابق با فرمول هرون، سطح مثلث (الف ب پ) برابر با 10.825 سانتیمتر مربع است. اکنون باید ارتفاع نظیر ضلع (ب پ) را محاسبه کنیم. این کار، با استفاده از فرمول مساحت مثلث بر اساس قاعده و ارتفاع انجام میشود. بر اساس این فرمول داریم:
A = (h b) ÷ 2
- A: مساحت (الف ب پ) و برابر با 10.825 سانتیمتر مربع
- b: قاعده (ب پ) و برابر با 5 سانتیمتر
- h: ارتفاع نظیر قاعده (ب پ)
با جایگذاری مقادیر بالا خواهیم داشت:
10.825 = (h 5) ÷ 2
10.825 2 = h 5
21.65 = h 5
21.65 ÷ 5 = h
4.33 = h
در نتیجه، ارتفاع نظیر ضلع (ب پ) برابر با 4.33 سانتیمتر است.
مساحت مثلث با نسبت های مثلثاتی
روابط و فرمولهای مثلثاتی، از پرکاربردترین ابزارهای محاسباتی در مسائل ریاضی هستند. این روابط (مخصوصا قانون سینوس ها و مقادیر سینوس زوایا)، به طور گسترده در محاسبات مربوط به مثلثها مورد استفاده قرار میگیرند.
در صورت بودن مشخص بودن برخی از زوایا و ضلعهای یک مثلث، میتوان از روش مثلثاتی برای تعیین مساحت استفاده کرد. حالتهای استفاده از این روش در محاسبه مساحت مثلث عبارت هستند از:
- مشخص بودن دو ضلع و زاویه بین (مثلث ض ز ض)
- مشخص بودن دو زاویه و ضلع بین (مثلث ز ض ز)
- مشخص بودن دو ضلع و زاویه غیر بین (مثلث ض ض ز)
- مشخص بودن دو زاویه و ضلع غیر بین (مثلث ز ز ض)
سطح مثلث با دو ضلع و زاویه بین
مساحت مثلث ض ز ض از ضرب دو ضلع در سینوس زاویه بین آنها تقسیم بر دو به دست میآید. برای درک بهتر این رابطه، مثلث زیر را در نظر بگیرید.
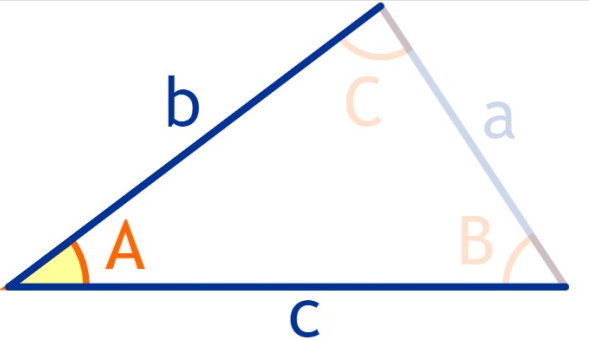
در مثلث بالا، مقادیر دو ضلع AC و AB به همراه زاویه A مشخص هستند. در این حالت، فرمول ریاضی برای تعیین مساحت مثلث با دو ضلع و زاویه بین به صورت زیر نوشته میشود:
- Area: مساحت
- b: طول ضلع AC
- c: طول ضلع AB
- A: زاویه راس A
در صورت مشخص بودن ضلعهای AC و BC به همراه زاویه C، رابطه مساحت به صورت در میآمد:
- b: طول ضلع AC
- a: طول ضلع BC
- C: زاویه راس C
به همین ترتیب، اگر ضلعهای AB و BC به همراه زاویه B مشخص بودند، فرمول مثلثاتی سطح مثلث برابر بود با:
- a: طول ضلع BC
- c: طول ضلع AB
- B: زاویه راس B
مثال: تعیین سطح مثلث با سینوس یک زاویه و طول دو ضلع
کشاورزی قصد دارد مساحت زمین زراعی خود را محاسبه کند. محدوده زمین مورد نظر، مشابه یک مثلث است. کشاورز، دو ضلع و زاویه بین آنها را اندازهگیری کرده و اطلاعات به دست آمده را بر روی تصویری مشابه زیر رسم میکند. با توجه به این اطلاعات، مساحت زمین چقدر است؟
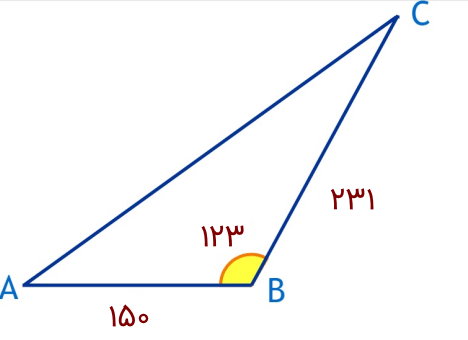
در مثلث بالا، طول ضلعهای AB و BC به همراه زاویه B برابر هستند با:
- c = AB = 150 m
- a = BC = 231 m
- B = 123°
به منظور تعیین مساحت مثلث به کمک سینوس، از فرمول مساحت مثلثهای ض ز ض استفاده میکنیم. این فرمول برای اطلاعات بالا به صورت زیر نوشته میشود:
مساحت زمین کشاورزی برابر 14530 متر مربع است.
سطح مثلث با دو زاویه و ضلع بین
تصویر زیر، یک مثلث ز ض ز یا مثلثی با دو زاویه و ضلع بین مشخص را نمایش میدهد.
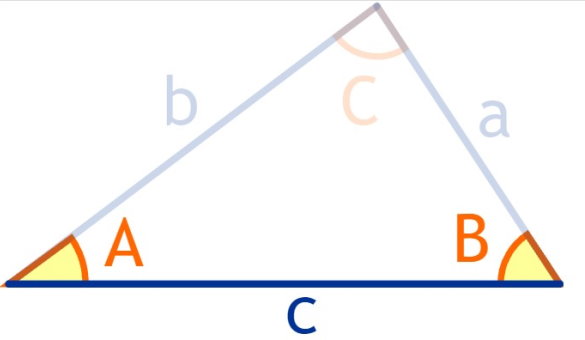
در مثلث بالا، مقدار زاویه A، ضلع AB و زاویه B مشخص است. در این حالت، فرمول محاسبه مساحت مثلث با دو زاویه و ضلع بین به صورت زیر نوشته میشود:
- Area: مساحت
- c: طول ضلع AB
- A: زاویه راس A
- B:زاویه راس B
- C: زاویه راس C
جمع زوایای داخلی مثلث، همواره برابر با 180 درجه است. به همین دلیل، با مشخص بودن زوایای A و B، زاویه C نیز از رابطه زیر به دست میآید:
برای حالتهای دیگر (مشخص بودن زوایا و ضلعهای دیگر) داریم:
مثال: تعیین سطح مثلث با سینوس زوایا و طول یک ضلع
تصویر زیر را در نظر بگیرید. در این تصویر، مقدار زوایای راسهای A و B به همراه طول ضلع AB مشخص شده است. بر اساس این اطلاعات و با استفاده از روابط مثلثاتی، مساحت مثلث را به دست آورید.
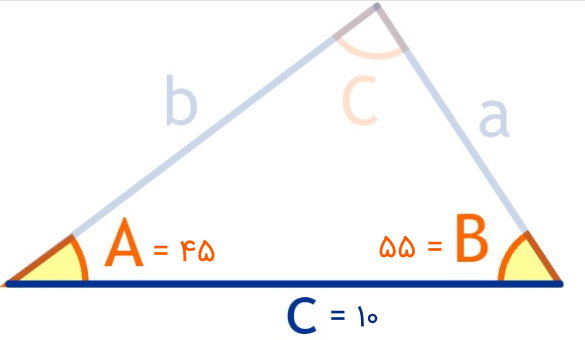
مطابق با فرمول محاسبه مساحت مثلث با دو زاویه و ضلع بین، داریم:
- Area: مساحت
- c: طول ضلع AB برابر با 10
- A: زاویه راس A برابر با 45 درجه
- B: زاویه راس B برابر با 55 درجه
- C: زاویه راس C برابر با (45+55)-180 یا 80 درجه
با جایگذاری مقادیر در فرمول، خواهیم داشت:
سطح مثلث با دو ضلع و زاویه غیر بین
مساحت مثلثهای ض ض ز (مثلث با دو ضلع و زاویه غیر بین)، معمولا با استفاده از ترکیب قانون سینوسها و یکی از روشهای قبلی (حالت ض ز ض، ز ض ز یا ض ض ض) محاسبه میشود. مثلث زیر را در نظر بگیرید.

مطابق با قانون سینوسها، رابطه زیر بین ضلعها و زوایای مثلث ABC برقرار است:
- a: طول ضلع BC
- A: زاویه راس A
- b: طول ضلع AC
- B: زاویه راس B
- c: طول ضلع AB
- C: زاویه راس C
با کمک نسبتهای مثلثاتی بالا، در صورت مشخص بودن دو ضلع و زاویه غیر بین، میتوان مقدار زاویه دوم، زاویه سوم (قانون جمع زوایای داخلی) و طول ضلع سوم را تعیین کرد. با مشخص شدن تمام ضلعها و زوایا، امکان محاسبه مساحت توسط روشهای قبلی فراهم میشود.
سطح مثلث با دو زاویه و ضلع غیر بین
محاسبه مساحت مثلثهای ز ز ض (مثلث با دو زاویه و ضلع غیر بین) نیز مانند حالت مثلث با دو ضلع و زاویه غیر بین است. مثلث زیر را در نظر بگیرید.
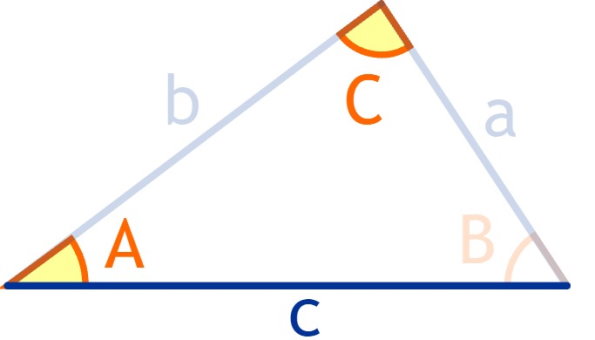
در مثلث ABC، زاویه A، زاویه C و ضلع AB مشخص هستند. با کمک قانون جمع زوایای داخلی، زاویه B به دست میآید. مطابق با قانون سینوسها نیز، ضلعهای AC و BC تعیین میشوند. با داشتن تمام زوایا و ضلعها، میتوان مساحت را به یکی از روشهای قبلی حل کرد.
سطح مثلث با سه زاویه
محاسبه مساحت مثلث با داشتن سه زاویه غیرممکن است. به دلیل مشخص نبودن ابعاد هیچ یک از ضلعهای مثلث در این حالت (مثلث ز ز ز)، امکان تعیین مساحت وجود ندارد. معلوم بودن تمام زوایای مثلث، فقط به تشخیص شکل آن کمک میکند. برای محاسبه مساحت، به طول یکی از ضلعها نیاز خواهد بود.

رابطه بین مساحت مثلث های متشابه چگونه است؟
نسبت مساحت مثلثهای متشابه برابر مربع نسبت ضلعهای متناظر آنها است. از روشهای تعیین اندازه سطح مثلثها میتوان به استفاده از مفهوم تشابه در اشکال هندسی اشاره کرد.
مثلثهای متشابه، مثلثهایی هستند که امکان تبدیل آنها توسط تغییر مقیاس، دوران، انتقال یا بازتاب محوری وجود دارد. به عنوان مثال، مثلثهای نمایش داده شده در تصویر زیر را در نظر بگیرید.
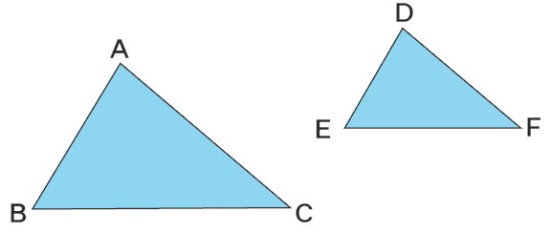
دو مثلث بالا، کاملا متشابه بوده و تنها تفاوت آنها، در ابعاد ضلعها است. رابطه ریاضی نسبت مساحتهای مثلثهای مشابه به صورت زیر نوشته میشود:
یا
مثال: تعیین سطح دو مثلث متشابه
تصویر زیر، دو مثلث متشابه را نمایش میدهد. اگر مساحت مثلث DEF برابر 40 سانتیمتر مربع، طول ضلع DF برابر 10 سانتیمتر و طول ضلع AC برابر 5 سانتیمتر باشد، سطح مثلث ABC چقدر خواهد بود؟
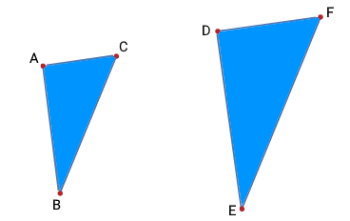
در این مثال، ضلعهای AC و DF، متناظر یکدیگر هستند. از اینرو، مطابق با رابطه اندازه سطح مثلثهای متشابه خواهیم داشت:
اطلاعات عددی مسئله را در رابطه بالا جایگزین میکنیم:
به این ترتیب، مساحت مثلث ABC برابر 10 سانتیمتر مربع است. همانطور که مشاهده میکنید، با وجود دو برابر بودن ابعاد ضلعهای متناظر (10 و 5 سانتیمتر)، اندازه سطح مثلث بزرگتر چهار برابر است (40 و 10 سانتیمتر مربع).
مساحت مثلث در دستگاه مختصات یا با مختصات سه راس
برای تعیین مساحت مثلث با مختصات سه راس باید با مفاهیم دستگاه مختصات و فاصله بین دو نقطه آشنا باشید. دستگاه مختصات یا مختصات هندسی، یکی از ابزارهای ریاضی برای تعیین محل قرارگیری نقاط بر روی صفحه دو بعدی یا فضای سه بعدی است.
مثلث، از سه راس و سه ضلع تشکیل میشود. در صورت مشخص بودن مختصات این سه راس بر روی دستگاه مختصات، میتوان سطح مثلث را تعیین کرد. در این حالت، سطح مثلث برابر سطح یا فضای اشغال شده توسط آن در مختصات هندسی خواهد بود. به عنوان مثال، سه نقطه با مشخصات زیر را در نظر بگیرید:
- نقطه A با مختصات (2,1-)
- نقطه B با مختصات (3,2)
- نقطه C با مختصات (1,5)
در صورت رسم این مثلثها در دستگاه مختصات، مشاهده خواهید کرد که این سه نقطه بر روی یک قرار ندارند. در نتیجه، با اتصال نقاط به یکدیگر، مثلث ABC تشکیل میشود.

سطح پوشش داده شده توسط مثلث ABC در دستگاه مختصات بالا، با رنگ آبی نمایش داده شده است.
فرمول محاسبه مساحت مثلث با مختصات سه راس
در صورت معلوم بودن مختصات سه راس مثلث در دستگاه مختصات هندسی، مساحت آن توسط رابطه زیر به دست میآید:
با توجه به اطلاعات مختصات نقاط داریم:
به این ترتیب، مساحت مثلث ABC با داشتن سه مختصات سه راس آن محاسبه شد.
فرمول محاسبه سطح مثلث با دترمینان
یکی دیگر از روشهای محاسبه سطح مثلثها با مختصات سه راس، استفاده از مفهوم دترمینان است. فرمول محاسبه اندازه سطح مثلث با دترمینان به صورت زیر نوشته میشود:
$$<br /\> \mathrm{K} = \frac{1}{2}\left|\begin{array}{\lll}<br /\> x_1 &\; y_1 &\; 1 \\<br /\> x_2 &\; y_2 &\; 1 \\<br /\> x_3 &\; y_3 &\; 1<br /\> \end{array}\right|<br /\> $$
- K: مساحت
- xA: مختصات راس A بر روی محور x
- yA: مختصات راس A بر روی محور y
- xB: مختصات راس B بر روی محور x
- yB: مختصات راس B بر روی محور y
- xC: مختصات راس C بر روی محور x
- yC: مختصات راس C بر روی محور y
به عنوان مثال، فرض کنید مختصات راسهای مثلث برابر با مقادیر زیر است:
- راس A با مختصات (1,1)
- راس B با مختصات (4,2)
- راس C با ختصات (3,5)
با جایگذاری مقادیر بالا در فرمول معرفی شده، داریم:
$$<br /\> \mathrm{K} = \frac{1}{2}\left|\begin{array}{\lll}<br /\> 1 &\; 1 &\; 1 \\<br /\> 4 &\; 2 &\; 1 \\<br /\> 3 &\; 5 &\; 1<br /\> \end{array}\right|<br /\> $$
رابطه بالا به صورت زیر حل میشود:
تعیین سطح مثلث با ضرب خارجی یا روش برداری
یکی دیگر از روشهای محاسبه مساحت مثلثها با استفاده از مختصات راسها، استفاده از مفاهیم مرتبط با محاسبات بردارها است. اندازه سطح مثلث در روش برداری، از ضرب خارجی بردارهای معرف دو ضلع تقسیم بر دو به دست میآید. تصویر زیر را در نظر بگیرید. در این تصویر، دو بردار از راس A به راسهای B و C رسم شدهاند.
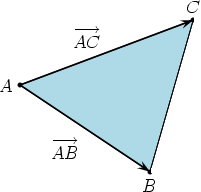
فرمول محاسبه اندازه سطح مثلث به روش برداری برابر است با:
- Area: مساحت
- : بردار رسم شده از راس A به راس B
- : بردار رسم شده از راس A به راس C
مثال: تعیین سطح مثلث به روش ضرب خارجی بردارها
مساحت مثلث ABC با مختصات راسهای زیر چقدر است؟
مطابق با رابطه تعیین سطح مثلثها به روش برداری، داریم:
با بازنویسی بردارها، رابطه بالا به شکل زیر در میآید:
در رابطه بالا، مقادیر راسها را جایگذاری میکنیم:
پس از انجام جمع برداری، به رابطه زیر میرسیم:
با ضرب خارجی بردارها، خواهیم داشت:
با محاسبه مقدار بردار حاصل از ضرب خارجی، تمام پارامترهای رابطه به مقادیر اسکالر تبدل میشوند:
در نتیجه:
مساحت مثلث برابر 7.5 است.
آزمون سنجش یادگیری مساحت مثلث
در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث مساحت مثلث را با طرح سوالهای چندگزینهای میسنجیم. پس از جواب دادن به تمام سوالها، نتیجه آزمون برای شما به نمایش درمیآید.
اندازه یک ضلع مثلثی برابر با 8 سانتیمتر است. اگر از راس مقابل به این ضلع، پارهخطی را بر روی آن عمود کنیم، طول پارهخط برابر با 6 سانتیمتر میشود. با توجه با این اطلاعات، مساحت مثلث را تعیین کنید.
24 سانتیمتر
24 سانتیمتر مربع
48 سانتیمتر
48 سانتیمتر مربع
مساحت مثلث با استفاده از رابطه زیر محاسبه میشود:
- A: مساحت مثلث
- b: قاعده مثلث
- h: ارتفاع نظیر قاعده مثلث
ضلعهای مثلث، همان قاعدههای این شکل در نظر گرفته میشوند. بنابراین، اندازه یکی از قاعدهها را داریم. به پارهخطی که از راس مقابل یک قاعده بر روی آن عمود میشود، ارتفاع نظیر قاعده میگویند. این اندازه نیز در صورت سوال آورده شده است. با قرار دادن مقادیر معلوم در فرمول بالا، به مساحت مثلث میرسیم:
در نتیجه، مساحت مثلث برابر با 24 سانتیمتر مربع است.
مساحت مثلثی به قاعده 11 سانتیمتر و ارتفاع نظیر 7 سانتیمتر چند است؟
37/5
38/5
49
84
مساحت مثلث با استفاده از رابطه زیر محاسبه میشود:
- A: مساحت مثلث
- b: قاعده مثلث
- h: ارتفاع نظیر قاعده مثلث
قاعده مثلث مورد سوال برابر با 11 واحد طول بوده و ارتفاع نظیر قاعده برابر با 7 واحد طول است. با جایگذاری این مقادیر در فرمول مساحت مثلث، خواهیم داشت:
در نتیجه، مساحت مثلث برابر با 38/5 واحد طول مربع است.
اندازه یکی از قاعدههای یک مثلث برابر با 6 واحد طول است. ارتفاع نظیر این قاعده در فاصله 1/5 واحد طول در بیرون مثلث قرار دارد. اگر اندازه این ارتفاع برابر با 5/8 واحد طول باشد، مساحت مثلث چقدر خواهد بود؟
17/4
18
21/75
27
مساحت مثلث با استفاده از رابطه زیر محاسبه میشود:
- A: مساحت مثلث
- b: قاعده مثلث
- h: ارتفاع نظیر قاعده مثلث
برای به دست آوردن مساحت، به ارتفاع نظیر یکی از ضلعها نیز نیاز داریم. ارتفاع 5/8، ارتفاع نظیر قاعده 6 است. توجه داشته باشید که ارتفاع مذکور، بیرون از مثلث قرار میگیرد. این موضوع، تاثیری در اندازه قاعده مورد استفاده در فرمول مساحت ندارد. با در نظر داشتن این نکته، اندازه قاعده و ارتفاع نظیر آن را درون فرمول قرار میدهیم:
در نتیجه، مساحت مثلث برابر با 17/4 واحد طول مربع است.
مساحت مثلثی برابر با 42 سانتیمتر مربع بوده و اندازه یکی از ضلعهای آن برابر با 12 سانتیمتر است. کدامیک از گزینههای زیر، اندازه ارتفاع نظیر این ضلع را نمایش میدهد؟
5 سانتیمتر
6 سانتیمتر
7 سانتیمتر
9 سانتیمتر
مساحت مثلث با استفاده از رابطه زیر محاسبه میشود:
- A: مساحت مثلث
- b: قاعده مثلث
- h: ارتفاع نظیر قاعده مثلث
اندازههای معلوم را درون فرمول بالا قرار میدهیم:
بنابراین، اندازه ارتفاع نظیر قاعده 12 سانتیمتری برابر با 7 سانتیمتر است.
اگر مساحت مثلثی برابر با 22/5 متر مربع بوده و اندازه یکی از ارتفاعهای آن برابر با 5 متر باشد، اندازه قاعده نظیر این ارتفاع چقدر خواهد بود؟
5 سانتیمتر
7 سانتیمتر
8 سانتیمتر
9 سانتیمتر
مساحت مثلث با استفاده از رابطه زیر محاسبه میشود:
- A: مساحت مثلث
- b: قاعده مثلث
- h: ارتفاع نظیر قاعده مثلث
مقادیر معلوم را درون فرمول بالا قرار میدهیم:
در نتیجه، قاعده نظیر ارتفاع 5 سانتیمتری برابر با 9 سانتیمتر است.
کدامیک از گزینههای زیر، مساحت مثلث متساویالاضلاعی به اندازه ضلع 14 سانتیمتر را نمایش میدهد؟
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
فرمول محاسبه مساحت مثلث متساویالاضلاع عبارت است از:
- A: مساحت مثلث متساویالاضلاع
- a: اندازه ضلع مثلث متساویالاضلاع
اندازه ضلع مثلث متساویالاضلاع برابر با 14 سانتیمتر است. این عدد را درون فرمول بالا قرار میدهیم:
در نتیجه، مساحت مثلث برابر با سانتیمتر مربع است.
مساحت مثلث قائمالزاویه متساویالساقین به اندازه ساق 1 سانتیمتر چیست؟
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
مساحت مثلث قائمالزاویه متساویالساقین، از رابطه زیر به دست میآید:
- A: مساحت مثلث قائمالزاویه متساویالساقین
- a: اندازه ساق مثلث قائمالزاویه متساویالساقین
اندازه ساق را درون رابطه بالا قرار میدهیم:
در نتیجه، مساحت مثلث قائمالزاویه متساویالساقین برابر با است.
مساحت مثلثی با ضلعهایی به اندازه 5، 7 و 8 اینچ کدام گزینه است؟
اینچ مربع
اینچ مربع
اینچ مربع
اینچ مربع
فرمول مساحت مثلث با سه ضلع (فرمول هرون) به صورت زیر نوشته میشود:
- A: مساحت مثلث
- s: نصف محیط مثلث
- a: طول ضلع اول
- b: طول ضلع دوم
- c: طول ضلع سوم
با توجه به پارامترهای این فرمول، ابتدا باید نصف محیط مثلث (s) را به دست بیاوریم:
اکنون، این مقدار را به همراه اندازه ضلعهای مثلث درون فرمول هرون قرار میهیم:
در نتیجه، مساحت مثلث برابر با است.
اندازه دو ضلع یک مثلث مختلفالاضلاع برابر با 5 و 9 سانتیمتر است. اگر زاویه داخلی بین این دو ضلع برابر با 37 درجه باشد، مساحت مثلث چقدر خواهد بود؟
10/2 سانتیمتر مربع
13/2 سانتیمتر مربع
13/5 سانتیمتر مربع
16/5 سانتیمتر مربع
فرمول محاسبه مساحت مثلث با استفاده از اندازه دو ضلع و زاویه بین عبارت است از:
- A: مساحت مثلث
- a: طول ضلع اول
- b: طول ضلع دوم
- C: زاویه راس بین ضلعهای a و b
اندازههای معلوم را درون فرمول بالا وارد میکنیم:
سینوس زاویه 37 درجه، تقریبا برابر با 0/6 است. بنابراین:
در نتیجه، مساحت مثلث برابر با 13/5 سانتیمتر مربع است.
مثلثی با دو ضلع 12/6 و 14/6 سانتیمتر را در نظر بگیرید. اگر زاویه بین این دو ضلع برابر با 82 درجه باشد، مساحت مثلث چقدر میشود؟
102/3
103/3
110/4
135/6
فرمول محاسبه مساحت مثلث با استفاده از اندازه دو ضلع و زاویه بین عبارت است از:
- A: مساحت مثلث
- a: طول ضلع اول
- b: طول ضلع دوم
- C: زاویه راس بین ضلعهای a و b
اندازههای معلوم را درون فرمول بالا وارد میکنیم:
سینوس زاویه 82 درجه، تقریبا برابر با 0/99 است. بنابراین:
در نتیجه، مساحت مثلث برابر با 102/3 سانتیمتر مربع است.
سخن آخر: محاسبه آنلاین مساحت مثلث
در این مقاله از مجله فرادرس بیشتر روشهای موجود برای محاسبه سطح مثلثها را مورد بررسی قرار دادیم. در صورتی که قصد انجام دستی این محاسبات را ندارید یا میخواهید از درست بودن مقادیر به دست آمده، اطمینان حاصل کنید، استفاده از ماشینحسابهای آنلاین و سایتهای تخصصی ریاضی، گزینه مناسبی است.
از بهترین ابزارهای آنلاین محاسبه اندازه سطح مثلث میتوان به موارد زیر اشاره کرد:
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان
- چگونه مساحت مثلث را حساب کنیم؟ + فیلم آموزشی و تمرین با جواب(همین مطلب)
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال
- فرمول هرون — به زبان ساده
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه — به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع













لطفامثالهای بی ربط نزنید چطوری مثلثی کشیدید که یک ضلع ان 6 ودیگر ضلع ان 4 و ضلع سوم ان 5 سانتیمتر است که یک زاویه باز دارد!!! اگر زحمت بکشید و خط کش و پرگار بیارید میبینید که اصلا زاویه باز در این نوع مثلثی که اضلاعش رو دادید نداریم .اگر قاعد رو 6 بگیریم و ضلع بعدی رو 4 سانتیمتر مثلث قایم ازایه هم اگر فرض شود ضلع سوم 7 سانتیمتر میشود نه 5 سانتیمتر!!!در ضمن اگر زاویه بین دو ضلع 6 و 4 سانت قایمه باشد ارتفاع همان 4 سانت است و به ازای هر درجه اضافه شدن زاویه ارتفاع کمتر ا ز4 سانت میشود عدد 8 رو از کجا اوردی ؟ و اگر 1 سانت به 6 سانت هم قبول کنیم ارتفاع حدود 3/7 خواهد شد و ضلع سوم تا 8 سانت طولش خواهد شد نه 5 سانت. خواهشی که دارم ریاضی را با دقت اموزش بدهید ریاضی علم اعداد و روابط حاکم میان انها هست روی هوا مثال اوردن درست نیست ممنون
با سلام و وقت بخیر؛
مثال مذکور اصلاح شد. با تشکر از دقت نظر شما.
سلامت و موفق باشید.
سلام وقت بخیر به من یک سوال دادن که اگر محیط مثلث 15/43 باشد اندازه قاعده آن چند است و ساق هاش با هم برابرند اندازه ساق هاش رو هم 4/32 داده باید چیکار کنم
سلام و وقت بخیر؛
محیط مثلث، جمع سه ضلع آن است. برای محاسبه قاعده مثلث متساوی الساقین از روی محیط و ساق، اندازه ساقها را ضربدر 2 کنید (۸/۶۴=۴/۳۲ × ۲) و عدد به دست آمده را از محیط کم کنید (۶/۷۹=۸/۶۴-۱۵/۴۳).
از همراهی شما با مجله فرادرس سپاسگزاریم. سلامت و موفق باشید.
علی بود
مثلث مختلف الاضلاع با زوایا ۱۲ و ۱۳ و ۵ داریم مساحت آن را بدست آورید
ممنون میشم به این پاسخ بدید
سلام. با استفاده از فرمول هرون میتوانید مساحت این مثلث را به دست آورید. برای آشنایی با فرمول هرون، به آموزش «فرمول هرون — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
از اینکه با مجله فرادرس همراه هستید، خوشحالیم.
خوب بود
بدون شرح! حرف نداشت
به نظر شما جواب مسئله اول که متوازی الاضلاع بود نباید ۱۰ میشد !؟ چطوری ۵ شده !؟
سلام، وقت شما بخیر؛
بله. این مورد اصلاح شد. ممنون از توجه شما.
از اینکه با مجله فرادرس همراه هستید، از شما سپاسگزاریم. سلامت و موفق باشید.
سلام یه سوال داشتم
مساحت هر مثلث از مساحت هر مربع بیشتره ؟
اگه نه یه مثال نقض بیارین ممنون
با سلام؛
مساحت هر مثلث لزوما از مساحت هر مربع بیشتر نیست. برای پسخگویی بهتر به این سوال، باید اندازه ضلعهای مثلث و مربع، نوع مثلث و محاط یا محیط بودن این شکلها مشخص باشد. به عنوان مثال، مساحت مربع محاطی در یک مثلث، همیشه از مساحت مثلث محیطی آن کمتر است. این نتیجه گیری با دانستن محاطی بودن مربع و محیطی بودن مثلث انجام میشود.
از همراهی شما با مجله فرادرس سپاسگزاریم. سلامت و موفق باشید.
باز هم روابطی هستند که فقط با دادن اندازه میانه مثلث یا ارتفاع ها فقط مساحت مثلث را به دست اورد
با تشکر از شما بابت مطالب علمی که گذاشتید .