چند ضلعی منتظم چیست؟ — به زبان ساده + فیلم آموزش رایگان و حل تمرین

چند ضلعی منتظم چند ضلعی است که تمام ضلع‌های آن باهم و تمام زاویه‌های آن با هم هم‌اندازه هستند. از شناخته شده‌ترین چندضلعی‌های منتظم می‌توان به مثلث متساوی الاضلاع و مربع اشاره کرد. در این آموزش، به معرفی کامل انواع چند ضلعی منتظم و اجزای آن‌ها نظیر زاویه داخلی، زاویه خارجی، زاویه مرکزی، شعاع، ارتفاع، قطر، محور تقارن و غیره می‌پردازیم. در بخش، ضمن ارائه فرمول‌‌های مربوطه، چندین مثال متنوع و کاربردی را نیز حل می‌کنیم.

فیلم آموزشی تعریف و ویژگی‌های چند‌ضلعی منتظم

چند ضلعی چیست و چه انواعی دارد؟

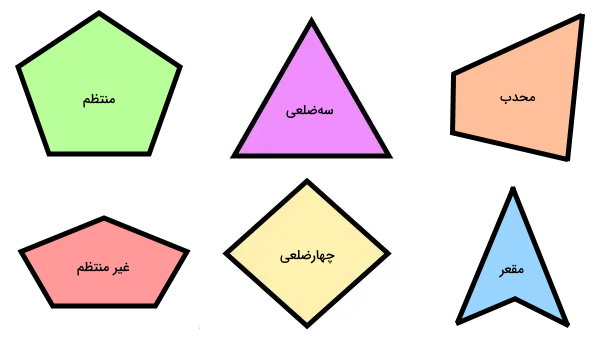
چند ضلعی، یکی از انواع شکل‌های هندسی است که از خط شکسته بسته تشکیل می‌شود. چندضلعی‌های محدب و مقعر، از انواع چندضلعی‌ها بر اساس اندازه زوایای داخلی هستند. از انواع چندضلعی‌ها بر اساس تعداد ضلع می‌توان به سه‌ضلعی، چهارضلعی، پنج‌ضلعی، شش‌ضلعی و غیره اشاره کرد. علاوه بر این، تمام چندضلعی‌ها در یکی از دو گروه چندضلعی‌های منتظم و غیر منتظم قرار می‌گیرند.

چند ضلعی منتظم چیست؟

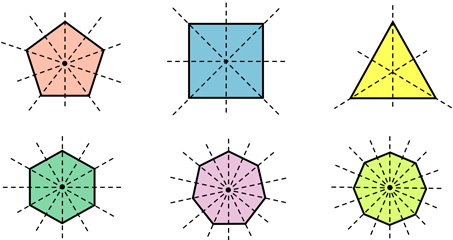
هرگاه در یک چندضلعی، تمام زاویه‌ها با هم و تمام ضلع‌ها با هم مساوی باشند، به آن چندضلعی منتظم می‌گویند. تصویر زیر، چند نمونه چند ضلعی منتظم را به همراه محورهای تقارن‌شان نمایش می‌دهد. از بین این موارد، مثلث متساوی الاضلاع (سه‌ضلعی منتظم) و مربع (چهارضلعی منتظم)، شناخته شده‌تر از دیگر چندضلعی‌های منتظم هستند.

اجزای چند ضلعی منتظم چه هستند؟

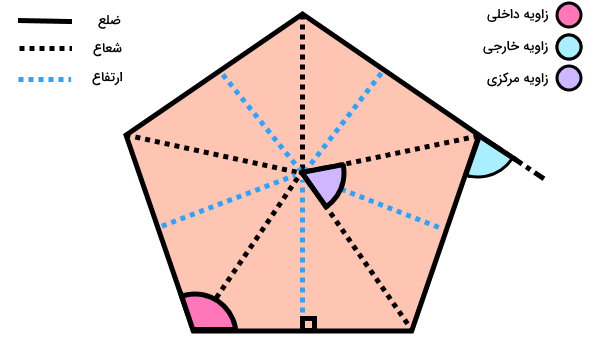
از مهم‌ترین اجزای چندضلعی‌های منتظم می‌توان زاویه داخلی، زاویه خارجی، ارتفاع، شعاع، زاویه مرکزی و ضلع را نام برد. تمام این اجزا در پنج‌ضلعی منتظم زیر نمایش داده شده‌اند. در بخش‌های بعدی، هر یک از اجزای چندضلعی‌های منتظم و نحوه محاسبه آن‌ها را توضیح خواهیم داد.

زاویه داخلی چند ضلعی منتظم چیست؟

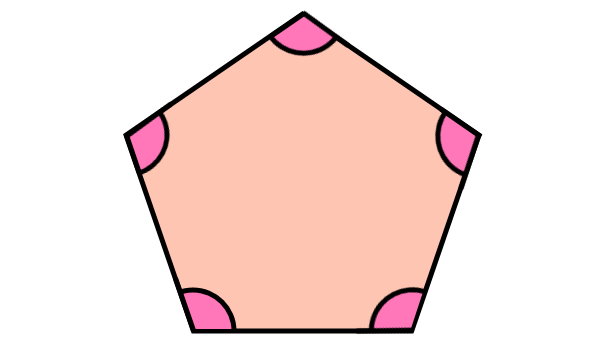
به زاویه بین دو راس (زاویه محل برخورد دو ضلع مجاور)، زاویه داخلی می‌گویند. یک n ضلعی منتظم، n زاویه داخلی با اندازه‌های برابر دارد.

فرمول محاسبه مجموع زوایای داخلی چند ضلعی منتظم

مجموع زوایای داخلی چند ضلعی منتظم برابر است با:

$$
S = ( n – ۲ ) \times ۱۸۰ ^ { \circ }
$$

• S: مجموع زوایای داخلی چندضلعی منتظم
• n: تعداد ضلع‌ها

فرمول بالا، برای تعیین مجموع زوایای داخلی تمام انواع چندضلعی‌ها قابل استفاده است.

مثال ۱: محاسبه مجموع زوایای داخلی مثلث متساوی الاضلاع

مجموع زوایای داخلی مثلث متساوی الاضلاع را حساب کنید.

مثلث متساوی الاضلاع، یک سه‌ضلعی منتظم است. مجموع زوایای داخلی این شکل هندسی توسط رابطه زیر محاسبه می‌شود:

$$
S = ( n – ۲ ) \times ۱۸۰ ^ { \circ }
$$

• S: مجموع زوایای داخلی مثلث متساوی الاضلاع
• n: تعداد ضلع‌های مثلث متساوی الاضلاع برابر با ۳

تعداد ضلع‌ها را درون فرمول قرار می‌دهیم:

$$
S = ( ۳ – ۲ ) \times ۱۸۰ ^ { \circ }
$$

$$
S = ( ۱ ) \times ۱۸۰ ^ { \circ }
$$

$$
S = ۱۸۰ ^ { \circ }
$$

در نتیجه، مجموع زوایای داخلی مثلث متساوی‌الاضلاع برابر با ۱۸۰ درجه است.

فرمول محاسبه هر زاویه چندضلعی منتظم

زوایای داخلی چندضلعی‌های منتظم هم‌اندازه هستند. با توجه به این نکته، اندازه هر یک از زاویه‌های داخلی یک n ضلعی منتظم را می‌توان توسط فرمول زیر محاسبه کرد:

$$
\alpha = \frac { ( n – ۲ ) \times ۱۸۰ ^ { \circ } } { n }
$$

مثال ۲: محاسبه زاویه راس‌های مربع

اندازه زاویه هر یک از راس‌های یک مربع را به دست بیاورید.

مربع، یک چهارضلعی منتظم است. احتمالا با اندازه زاویه هر یک از راس‌های این شکل آشنا باشید. به هر حال، این اندازه از رابطه زیر به دست می‌آید:

$$
\alpha = \frac { ( n – ۲ ) \times ۱۸۰ ^ { \circ } } { n }
$$

• α: اندازه زاویه داخلی مربع
• n: تعداد ضلع‌های مربع برابر با ۴

$$
\alpha = \frac { ( ۴ – ۲ ) \times ۱۸۰ ^ { \circ } } { ۴ }
$$

$$
\alpha = \frac { ( ۲ ) \times ۱۸۰ ^ { \circ } } { ۴ }
$$

$$
\alpha = \frac { ۳۶۰ ^ { \circ } } { ۴ }
$$

$$
\alpha = \frac { ( n – ۲ ) \times ۱۸۰ ^ { \circ } } { n }
$$

$$
\alpha = ۹۰ ^ { \circ }
$$

در نتیجه، زاویه هر راس مربع برابر با ۹۰ درجه است.

زاویه خارجی چند ضلعی منتظم چیست؟

با امتداد دادن هر ضلع چندضلعی منتظم، بین امتداد و ضلع مجاورش، زاویه‌ای به وجود می‌آید که به آن، زاویه خارجی گفته می‌شود. هر n ضلعی منتظم، n زاویه خارجی دارد. زوایای خارجی چندضلعی منتظم نیز مانند زوایای داخلی آن هم‌اندازه هستند.

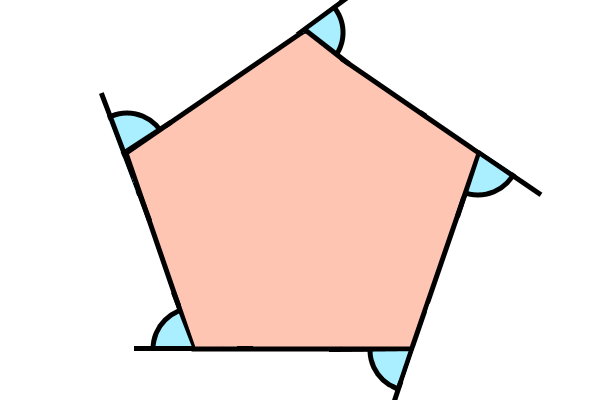
رابطه بین زاویه داخلی و زاویه خارجی چند ضلعی منتظم

مجموع هر زاویه داخلی چندضلعی منتظم با زاویه خارجی مجاور آن، ۱۸۰ درجه می‌شود. به عبارت دیگر، زوایای داخلی و خارجی مجاور، مکمل یکدیگر هستند.

۱۸۰° = زاویه خارجی + زاویه داخلی

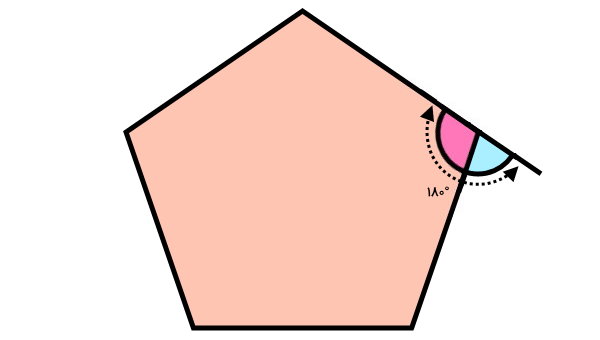
مجموع زوایای خارجی چند ضلعی منتظم

مجموع زوایای خارجی تمام چندضلعی‌های منتظم برابر با ۳۶۰ درجه است. به دلیل برابر بودن این زاویه‌ها با هم، فرمول اندازه زاویه خارجی چند ضلعی منتظم به صورت زیر نوشته می‌شود:

$$
\beta = \frac { ۳۶۰ ^ { \circ } } { n }
$$

مثال ۳: تعیین مجموع زوایای خارجی پنج ضلعی منتظم

اندازه زاویه خارجی یک چندضلعی منتظم برابر با ۷۲ درجه است. این چندضلعی چیست و مجموع زوایای خارجی آن چقدر است؟

چندضلعی‌های منتظم، بر اساس تعداد ضلع‌هایشان تقسیم‌بندی می‌شوند. تعداد ضلع‌های چندضلعی مورد سوال، با استفاده از فرمول زیر تعیین می‌شود:

$$
\beta = \frac { ۳۶۰ ^ { \circ } } { n }
$$

• β: زاویه خارجی چندضلعی منتظم برابر با ۷۲ درجه
• n: تعداد ضلع‌های چندضلعی منتظم

اندازه معلوم را درون فرمول بالا قرار می‌دهیم و آن را بر حسب تعداد ضلع‌ها (n) حل می‌کنیم:

$$
۷۲ ^ { \circ } = \frac { ۳۶۰ ^ { \circ } } { n }
$$

$$
n = \frac { ۳۶۰ ^ { \circ } } { ۷۲ ^ { \circ } }
$$

$$
n = ۵
$$

بنابراین، در اینجا با یک پنج‌ضلعی منتظم مواجهه هستیم. اندازه تمام زاویه‌های خارجی چندضلعی‌های منتظم با هم برابر است. به این ترتیب، داریم:

۷۲° + ۷۲° + ۷۲° + ۷۲° + ۷۲° = مجموع زوایای خارجی پنج‌ضلعی منتظم

۳۶۰° = مجموع زوایای خارجی پنج‌ضلعی منتظم

مجموع زوایای خارجی پنج‌ضلعی منتظم، مانند تمام چندضلعی‌های منتظم، برابر با ۳۶۰ درجه است.

ارتفاع چند ضلعی منتظم چیست ؟

«ارتفاع» (Apothem)، پاره‌خطی است که مرکز چندضلعی منتظم را به مرکز ضلع‌های آن متصل می‌کند. ارتفاع چندضلعی منتظم بر ضلع‌های آن عمود می‌شود. به عبارن دیگر، ارتفاع، عمود منصف ضلع‌های چندضلعی منتظم است. یک n ضلعی منتظم، n ارتفاع با اندازه‌های برابر دارد.

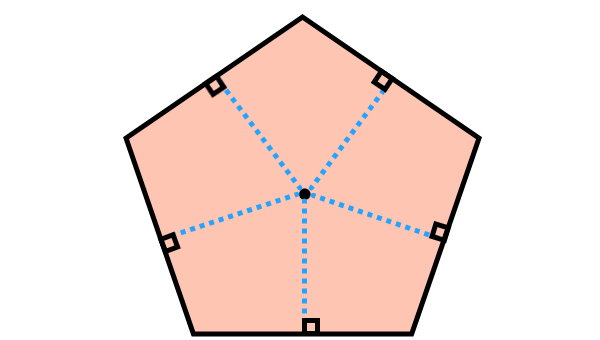
بر اساس روابط مثلثاتی، فرمول ارتفاع چند ضلعی منتظم عبارت است از:

$$
a = \frac { s } { ۲ \tan { \frac { ۱۸۰ ^ { \circ } } { n } } }
$$

• a: ارتفاع چندضلعی منتظم
• s: طول ضلع چندضلعی منتظم
• n: تعداد ضلع‌ها

ارتفاع چندضلعی منتظم، برابر با شعاع دایره محاطی درون آن است. اگر یک دایره را به گونه‌ای رسم کنیم که تمام ضلع‌های چندضلعی منتظم بر محیط آن مماس شوند، شعاع دایره با ارتفاع چندضلعی منتظم برابر خواهد بود.

شعاع دایره محاط در چندضلعی منتظم معمولا با حرف r نمایش داده می‌شوند. بر اساس این قاعده نام‌گذاری داریم:

$$
a = r
$$

مثال ۴: محاسبه ارتفاع شش ضلعی منتظم

اندازه ارتفاع یک شش‌ضلعی منتظم به طول ضلع ۳ سانتی‌متر را به دست بیاورید.

با قرار دادن اندازه‌های معلوم در فرمول زیر، ارتفاع شش‌ضلعی منتظم به دست می‌آید:

$$
a = \frac { s } { ۲ \tan { \frac { ۱۸۰ ^ { \circ } } { n } } }
$$

• a: ارتفاع شش‌ضلعی منتظم
• s: طول ضلع شش‌ضلعی منتظم برابر با ۳ سانتی‌متر
• n: تعداد ضلع‌ها برابر با ۶

$$
a = \frac { ۳ } { ۲ \tan { \frac { ۱۸۰ ^ { \circ } } { ۶ } } }
$$

$$
a = \frac { ۳ } { ۲ \tan { ۳۰ ^ { \circ } } }
$$

تانژانت زاویه ۳۰ درجه، تقریبا برابر با ۰/۵۸ است:

$$
a = \frac { ۳ } { ۲ \times ۰/۵۸ }
$$

$$
a = \frac { ۳ } { ۱/۱۶ }
$$

$$
a = ۲/۵۹
$$

در نتیجه، ارتفاع شش‌ضلعی منتظم برابر با ۲/۵۹ سانتی‌متر است.

مثال ۵: محاسبه طول ضلع چندضلعی منتظم از روی ارتفاع

ارتفاع یک چهارضلعی منتظم برابر با ۱۵ متر است. اندازه هر یک از ضلع‌های چهارضلعی را حساب کنید.

بر اساس رابطه ارتفاع چندضلعی‌های منتظم، داریم:

$$
a = \frac { s } { ۲ \tan { \frac { ۱۸۰ ^ { \circ } } { n } } }
$$

• a: ارتفاع چهارضلعی منتظم برابر با ۱۵ متر
• s: طول ضلع چهارضلعی
• n: تعداد ضلع‌ها برابر با ۴

با قرار دادن اندازه‌های معلوم در فرمول بالا و بازنویسی آن بر حسب s، طول هر ضلع به دست می‌آید:

$$
۱۵ = \frac { s } { ۲ \tan { \frac { ۱۸۰ ^ { \circ } } { ۴ } } }
$$

$$
۱۵ = \frac { s } { ۲ \tan { ۴۵ ^ { \circ } } }
$$

$$
s = ۱۵ \times ۲ \tan { ۴۵ ^ { \circ } }
$$

تانژانت زاویه ۴۵ درجه برابر با یک است:

$$
s = ۱۵ \times ۲ \times ۱
$$

$$
s = ۳۰
$$

در نتیجه، اندازه هر یک از ضلع‌های چهارضلعی منتظم برابر با ۳۰ متر است.

شعاع چند ضلعی منتظم چیست ؟

به فاصله مرکز چندضلعی منتظم تا هر یک از راس‌های آن، شعاع می‌گویند. شعاع، هر یک از زاویه‌های داخلی را به دو زاویه برابر تقسیم می‌کند. به عبارت دیگر، شعاع چندضلعی منتظم، نیمساز زاویه‌های داخلی آن است. هر n ضلعی منتظم، n شعاع با اندازه‌های مساوی دارد. اندازه شعاع‌های چندضلعی منتظم با شعاع دایره محیطی گذرنده از راس‌های آن برابر است.

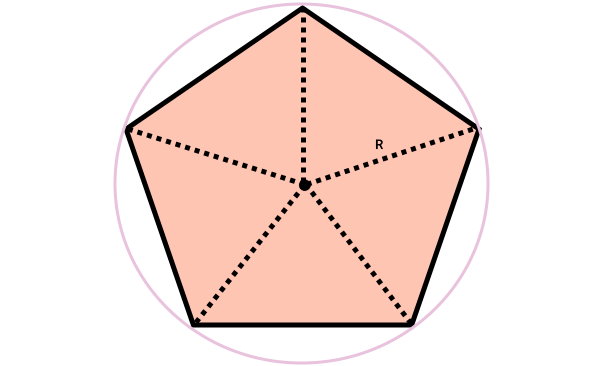
شعاع چندضلعی منتظم با عنوان «شعاع دایره محیطی» (Circumradius) نیز شناخته می‌شود. فرمول شعاع چند ضلعی منتظم عبارت است از:

$$
R = \frac { s } { ۲ \sin { \frac { ۱۸۰ ^ { \circ } } { n } } }
$$

• R: شعاع چندضلعی منتظم (شعاع دایره محیطی)
• s: طول ضلع چندضلعی منتظم
• n: تعداد ضلع‌ها

در صورت رسم ارتفاع‌‌ها و شعاع‌ها، چندضلعی منتظم به مجموعه‌ای از مثلث‌های قائم الزاویه تقسیم می‌شود. تصویر زیر، یکی از این مثلث‌ها را نمایش می‌دهد. شعاع چندضلعی منتظم، وتر مثلث و ارتفاع آن، یکی از ساق‌های مثلث است.

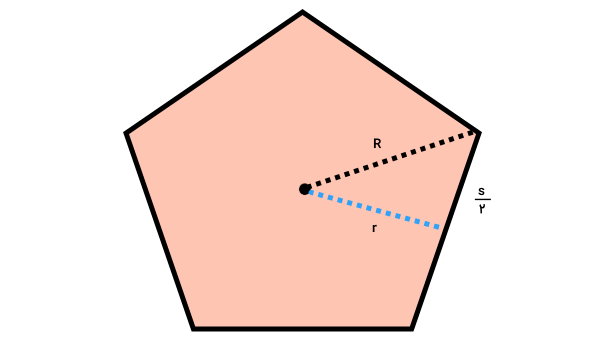
ارتفاع چندضلعی منتظم (r یا a)، عمود منصف ضلع‌های آن است. بنابراین، ساق دیگر مثلث قائم الزاویه بالا، نصف ضلع (s/۲) خواهد بود. به این ترتیب، می‌توانیم قضیه فیثاغورس را بین اندازه‌های شعاع، ارتفاع و ضلع بنویسیم:

$$
R ^ { ۲ } = r ^ { ۲ } + ( \frac { s } { ۲ } ) ^ { ۲ }
$$

• R: شعاع چندضلعی منتظم
• r: ارتفاع چندضلعی منتظم (شعاع دایره محاطی)
• s: طول ضلع چندضلعی منتظم

علاوه بر فرمول بالا، رابطه بین شعاع دایره محاطی (r و a) با شعاع دایره محیطی به صورت زیر نیز نوشته می‌شود:

$$
r = R \times \cos \frac { ۱۸۰ ^ { \circ } }{ n }
$$

$$
R = \frac { r } { \cos \frac { ۱۸۰ ^ { \circ } }{ n } }
$$

با استفاده از روابط مثلثاتی و قضیه فیثاغورس، اندازه‌های مختلف چندضلعی منتظم را می‌توان به راحتی به یکدیگر تبدیل کرد.

مثال ۶: محاسبه شعاع چندضلعی منتظم

ارتفاع یک هشت‌ضلعی منتظم برابر با ۸ متر و اندازه ضلع‌های آن برابر با ۱۲ متر است. شعاع هشت‌ضلعی منتظم را به دست بیاورید.

به منظور تعیین شعاع از روی ارتفاع و ضلع، بهترین گزینه، استفاده از قضیه فیثاورس است. بر اساس این قضیه، رابطه بین اندازه‌های مذکور به صورت زیر نوشته می‌شود:

$$
R ^ { ۲ } = a ^ { ۲ } + ( \frac { s } { ۲ } ) ^ { ۲ }
$$

• R: شعاع هشت‌ضلعی منتظم
• a: ارتفاع هشت‌‌ضلعی منتظم برابر با ۸ متر
• s: طول ضلع هشت‌ضلعی منتظم برابر با ۱۲ متر

$$
R ^ { ۲ } = ۸ ^ { ۲ } + ( \frac { ۱۲ } { ۲ } ) ^ { ۲ }
$$

$$
R ^ { ۲ } = ۸ ^ { ۲ } + ۶ ^ { ۲ }
$$

$$
R ^ { ۲ } = ۶۴ + ۳۶
$$

$$
R ^ { ۲ } = ۱۰۰
$$

$$
R = \sqrt { ۱۰۰ }
$$

$$
R = ۱۰
$$

در نتیجه، شعاع هشت‌ضلعی منتظم برابر با ۱۰ متر است.

مثال ۷: تعیین تعداد ضلع‌های چندضلعی منتظم

طول ضلع یک چندضلعی منتظم با اندازه شعاع آن برابر است. نام این چندضلعی منتظم چیست؟

به منظور تعیین نوع چندضلعی منتظم، باید تعداد ضلع‌های آن را مشخص کنیم. فرمول زیر، هر سه اندازه ارتفاع، شعاع و تعداد ضلع‌ها را در خود دارد. بنابراین، بررسی این فرمول می‌تواند به ما در تعیین نوع چندضلعی منتظم کمک کند.

$$
R = \frac { s } { ۲ \sin { \frac { ۱۸۰ ^ { \circ } } { n } } }
$$

• R: شعاع چندضلعی منتظم (شعاع دایره محیطی)
• s: طول ضلع چندضلعی منتظم
• n: تعداد ضلع‌ها

به دلیل برابر بودن شعاع (R) و ضلع (s)، آن‌ها را از دو طرف فرمول خط می‌زنیم:

$$
۱ = \frac { ۱ } { ۲ \sin { \frac { ۱۸۰ ^ { \circ } } { n } } }
$$

$$
۲ \sin { \frac { ۱۸۰ ^ { \circ } } { n } } = ۱
$$

$$
\sin { \frac { ۱۸۰ ^ { \circ } } { n } } = \frac { ۱ } { ۲ }
$$

سینوس زاویه ۳۰ درجه برابر با یک‌دوم است. بنابراین، داریم:

$$
\sin { \frac { ۱۸۰ ^ { \circ } } { n } } = \sin { ۳۰ ^ { \circ } } = \frac { ۱ } { ۲ }
$$

$$
\frac { ۱۸۰ ^ { \circ } } { n } = ۳۰ ^ { \circ }
$$

$$
n = \frac { ۱۸۰ ^ { \circ } } { ۳۰ ^ { \circ } }
$$

$$
n = ۶
$$

تعداد ضلع‌های چندضلعی منتظم برابر با ۶ است. بنابراین، در شش‌ضلعی منتظم، اندازه شعاع و ضلع با هم برابر هستند.

مثال ۸: محاسبه طول ضلع هفت ضلعی منتظم

دایره‌ای به شعاع ۱۸ سانتی‌متر را بر یک هفت‌ضلعی منتظم محیط کرده‌ایم. اندازه ضلع‌های هفت‌ضلعی چقدر است؟

به منظور تعیین طول ضلع هفت‌ضلعی منتظم، فرمول زیر را می‌نویسیم:

$$
R = \frac { s } { ۲ \sin { \frac { ۱۸۰ ^ { \circ } } { n } } }
$$

• R: شعاع دایره محیط بر هفت‌ضلعی منتظم برابر با ۱۸ سانتی‌متر
• s: طول ضلع هفت‌ضلعی منتظم
• n: تعداد ضلع‌ها برابر با ۷

$$
۱۸ = \frac { s } { ۲ \sin { \frac { ۱۸۰ ^ { \circ } } { ۷ } } }
$$

$$
۱۸ = \frac { s } { ۲ \sin { ۲۵/۷۱ ^ { \circ } } }
$$

سینوس زاویه ۲۵/۷۱ درجه، حدودا برابر ۰/۴۳ است:

$$
۱۸ = \frac { s } { ۲ \times ۰/۴۳ }
$$

$$
۱۸ = \frac { s } { ۰/۸۶ }
$$

$$
s = ۰/۸۶ \times ۱۸
$$

$$
s = ۱۵/۴۸
$$

در نتیجه، اندازه هر ضلع هفت‌ضلعی منتظم برابر با ۱۵/۴۸ سانتی‌متر است.

زاویه مرکزی چند ضلعی منتظم چیست؟

زاویه مرکزی، زاویه بین دو شعاع مجاور چندضلعی منتظم است. اگر چندضلعی منتظم را به همراه دایره محیط بر آن در نظر بگیریم، زاویه مرکزی، همان زاویه مقابل کمان گذرنده از راس‌های یک ضلع خواهد بود. مجموع زوایای مرکزی یک دایره برابر با ۳۶۰ درجه است. بنابراین، مجموع زوایای مرکزی چندضلعی منتظم نیز برابر با ۳۶۰ درجه می‌شود.

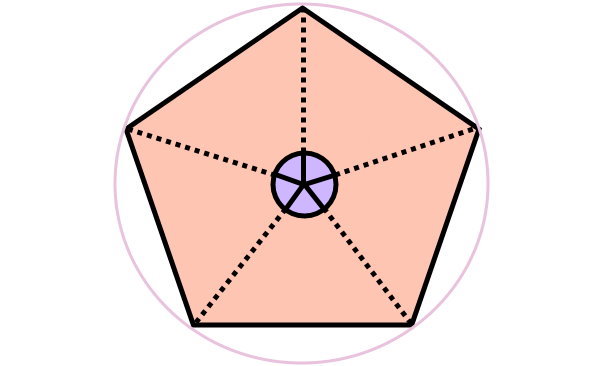
یک n ضلعی منتظم، n زاویه مرکزی با اندازه‌های برابر دارد. از این‌رو، فرمول زاویه مرکزی چندضلعی منتظم عبارت است از:

$$
\theta = \frac { ۳۶۰ ^ { \circ } } { n }
$$

• θ: زاویه مرکزی چندضلعی منتظم
• n: تعداد ضلع‌ها

به منظور تعیین زاویه مرکزی و زاویه داخلی چندضلعی منتظم، فقط به تعداد ضلع‌های آن نیاز داریم. در یک چندضلعی منتظم، ارتفاع، نیم‌ساز زاویه مرکزی و شعاع، نیم‌ساز زاویه داخلی است. علاوه بر این، ارتفاع، ضلع را با زاویه راست (۹۰ درجه) قطع می‌کند. بنابراین، با مشخص بودن تعداد ضلع‌ها، می‌توان تمام زاویه‌های مربوط به چندضلعی منتظم را به دست آورد.

مثال ۹: محاسبه زاویه مرکزی چندضلعی منتظم

زاویه مقابل به هر ضلع یک ده‌ضلعی منتظم چقدر است؟

به منظور تعیین زاویه مقابل به هر ضلع یا زاویه مرکزی چندضلعی‌های منتظم، عدد ۳۶۰ را بر تعداد ضلع‌ها تقسیم می‌کنیم:

$$
\theta = \frac { ۳۶۰ ^ { \circ } } { n }
$$

• θ: زاویه مرکزی ده‌ضلعی منتظم
• n: تعداد ضلع‌ها برابر ۱۰

$$
\theta = \frac { ۳۶۰ ^ { \circ } } { n }
$$

$$
\theta = \frac { ۳۶۰ ^ { \circ } } { ۱۰ }
$$

$$
\theta = ۳۶ ^ { \circ }
$$

هر یک از زوایای مرکزی ده‌ضلعی منتظم برابر با ۳۶۰ درجه است.

ضلع، راس و قطر چند ضلعی منتظم چیست ؟

ضلع‌ها، پاره‌خط‌هایی هستند که محیط چندضلعی منتظم را تشکیل می‌دهند. به محل برخورد ضلع‌ها، راس یا گوشه می‌گویند. زاویه بین دو ضلع یا زاویه هر راس، با عنوان زاویه داخلی شناخته می‌شود. در بخش‌های قبلی، نحوه اندازه‌گیری این زاویه را توضیح دادیم. هر n ضلعی منتظم، n ضلع مساوی و n راس با زاویه‌های هم‌اندازه دارد.

ضلع، از اندازه‌های مهم در تعیین محیط و مساحت چندضلعی منتظم است. راس نیز برای تعریف یکی دیگر از اجزای چندضلعی، به نام قطر، مورد استفاده قرار می‌گیرد. قطر چندضلعی منتظم، پاره‌خطی است که از هر راس به راس‌های غیر مجاور رسم می‌شود. تصویر زیر، قطرهای رسم شده از یک راس پنج‌ضلعی منتظم را نمایش می‌دهد.

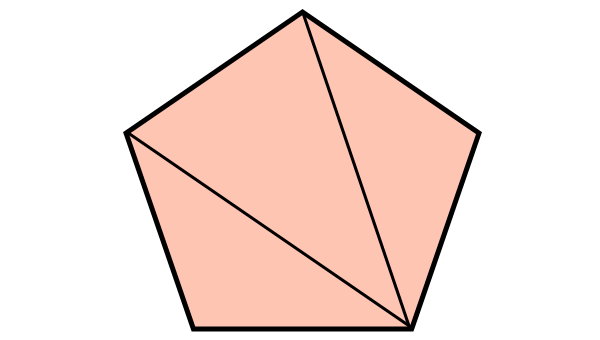
با اتصال راس‌های دیگر به راس‌های غیر مجاورشان، تمام قطرهای چندضلعی به دست می‌آیند. تمام قطرهای چندضلعی منتظم درون آن قرار می‌گیرند. فقط در چندضلعی‌های مقعر، یک یا چند قطر، از شکل خارجی می‌شوند.

فرمول محاسبه تعداد قطرهای چند ضلعی منتظم

فرمول تعداد قطرهای چند ضلعی منتظم به صورت زیر نوشته می‌شود:

$$
d_n = \frac { n ( n – ۳ ) } { ۲ }
$$

• d_n: تعداد قطرهای چندضلعی منتظم
• n: تعداد ضلع‌های چندضلعی منتظم

مثال ۱۰: تعیین تعداد قطرهای چندضلعی منتظم

نسبت تعداد قطرهای دوازده‌ضلعی منتظم به شش‌ضلعی منتظم را حساب کنید.

تعداد قطرهای دوازده‌ضلعی منتظم از رابطه زیر به دست می‌آید:

$$
d_n = \frac { n ( n – ۳ ) } { ۲ }
$$

$$
d_ { ۱۲ } = \frac { ۱۲ \times ( ۱۲ – ۳ ) } { ۲ }
$$

$$
d_ { ۱۲ } = \frac { ۱۲ \times ۹ } { ۲ }
$$

$$
d_ { ۱۲ } = ۶ \times ۹
$$

$$
d_ { ۱۲ } = ۵۴
$$

تعداد قطرهای شش‌ضلعی منتظم نیز به صورت زیر محاسبه می‌شود:

$$
d_n = \frac { n ( n – ۳ ) } { ۲ }
$$

$$
d_۶ = \frac { ۶ \times ( ۶ – ۳ ) } { ۲ }
$$

$$
d_۶ = \frac { ۶ \times ۳ } { ۲ }
$$

$$
d_۶ = ۳ \times ۳
$$

$$
d_۶ = ۹
$$

در نتیجه، نسبت تعداد قطرهای دوازده‌ضلعی منتظم به شش‌ضلعی منتظم عبارت است از:

$$
\frac { d_ { ۱۲ } } { d_۶ } = \frac { d_ { ۵۴ } } { ۹ } = ۶
$$

فرمول تعداد اضلاع چند ضلعی منتظم

در تمام فرمول‌های محاسبه اندازه‌های مختلف چندضلعی‌های منتظم، تعداد ضلع‌ها به صورت مستقیم یا غیر مستقیم به کار گرفته می‌شود. از این‌رو، با بازنویسی این فرمول‌ها بر حسب n، می‌توان تعداد ضلع‌های چندضلعی منتظم را به دست آورد. به عنوان مثال، اگر مجموع زوایای داخلی را داشته باشیم، فرمول تعداد ضلع چند ضلعی منتظم به صورت زیر نوشته می‌شود:

$$
n = \frac { S } { ۱۸۰ ^ { \circ } } + ۲
$$

• n: تعداد ضلع‌های چندضلعی منتظم
• S: مجموع زوایای داخلی چندضلعی منتظم

به همین ترتیب، با دانستن زاویه داخلی، زاویه خارجی، مجموع زوایای خارجی، تعداد قطرها و غیره، امکان محاسبه تعداد ضلع‌ها فراهم می‌شود. تعداد ضلع‌های چندضلعی منتظم، در محاسبه محیط و مساحت مورد استفاده قرار می‌گیرد.

مثال ۱۱: محاسبه تعداد ضلع‌های چندضلعی منتظم

مجموع زوایای داخلی یک چندضلعی منتظم برابر با ۱۴۴۰ درجه است. تعداد ضلع‌های این چندضلعی را به دست بیاورید.

فرمول محاسبه تعداد ضلع‌های چندضلعی منتظم بر حسب مجموع زوایای داخلی آن برابر است با:

$$
n = \frac { S } { ۱۸۰ ^ { \circ } } + ۲
$$

• n: تعداد ضلع‌های چندضلعی منتظم
• S: مجموع زوایای داخلی برابر با ۱۴۴۰

$$
n = \frac { ۱۴۴۰ ^ { \circ } } { ۱۸۰ ^ { \circ } } + ۲
$$

$$
n = ۸ + ۲
$$

$$
n = ۱۰
$$

در نتیجه، تعداد ضلع‌های چندضلعی منتظم برابر با ۱۰ است.

محیط چند ضلعی منتظم چگونه بدست می آید؟

محیط چندضلعی منتظم از جمع اندازه ضلع‌های آن با یکدیگر به دست می‌آید. محیط، اندازه دو یک شکل هندسی است. به عنوان مثال، اگر هر پنج ضلع پنج‌ضلعی زیر را با یکدیگر جمع کنیم، محیط آن محاسبه می‌شود.

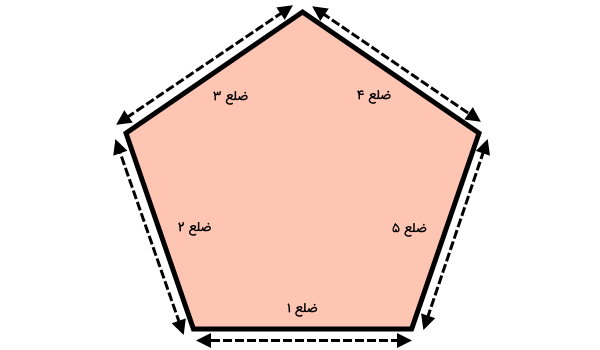
محیط پنج‌ضلعی بالا برابر است با:

ضلع ۵ + ضلع ۴ + ضلع ۳ + ضلع ۲ + ضلع ۱ = محیط پنج‌ضلعی

چندضلعی‌های منتظم، ضلع‌هایی با اندازه مساوی دارند. بنابراین، داریم:

ضلع + ضلع + ضلع + ضلع + ضلع = محیط پنج‌ضلعی

رابطه بالا را می‌توانیم به صورت ضرب اندازه یک ضلع در تعداد ضلع‌ها بنویسیم:

ضلع × ۵ = محیط پنج‌ضلعی

فرمول محیط چندضلعی منتظم

فرمول کلی محیط چندضلعی منتظم به صورت «ضلع × تعداد ضلع‌ها» نوشته می‌شود. عبارت جبری این فرمول عبارت است از:

$$
P = n s
$$

• P: محیط چندضلعی منتظم
• n: تعداد ضلع‌های چندضلعی منتظم
• s: اندازه هر ضلع

جدول زیر، محیط برخی از چندضلعی‌های منتظم را نمایش می‌دهد.

عنوان چندضلعی منتظم	فرمول محیط
مثلث متساوی الاضلاع	P = ۳s
مربع	P = ۴s
پنج‌ضلعی منتظم	P = ۵s
شش‌ضلعی منتظم	P = ۶s
هفت‌ضلعی منتظم	P = ۷s
هشت‌ضلعی منتظم	P = ۸s
نه‌ضلعی منتظم	P = ۹s
ده‌ضلعی منتظم	P = ۱۰s

فرمول کلی محیط چندضلعی منتظم، بسیار ساده است. با این وجود، در صورت مشخص نبودن اندازه ضلع یا تعداد ضلع‌ها، ابتدا باید با استفاده از فرمول‌ها و روش‌های معرفی شده در بخش‌های قبل، این اندازه‌ها را به دست آورد و در رابطه محیط قرار داد.

مثال ۱۲: محاسبه محیط پنج ضلعی منتظم

اندازه هر ضلع یک پنج‌ضلعی منتظم برابر با ۱۹ سانتی‌متر است. محیط پنج‌ضلعی منتظم را حساب کنید.

محیط پنج‌ضلعی منتظم از فرمول زیر به دست می‌آید:

$$
P = n s
$$

• P: محیط پنج‌ضلعی منتظم
• n: تعداد ضلع‌ها برابر با ۵
• s: اندازه هر ضلع برابر با ۱۹ سانتی‌متر

$$
P = ۵ \times ۱۹
$$

$$
P = ۹۵
$$

محیط پنج‌ضلعی منتظم برابر با ۹۵ سانتی‌متر است.

مساحت چند ضلعی منتظم چگونه بدست می آید؟

مساحت چندضلعی منتظم یا سطح درون آن، با استفاده از تعداد ضلع‌ها، اندازه هر ضلع و ارتفاع به دست می‌آید رابطه محاسبه مساحت چندضلعی منتظم عبارت است از:

۲ ÷ (طول یک ضلع × تعداد ضلع‌ها × ارتفاع چند ضلعی) = مساحت چند ضلعی منتظم

حاصل‌ضرب یک ضلع در تعداد ضلع‌ها، محیط چندضلعی منتظم را نمایش می‌دهد. بنابراین، می‌توانیم رابطه بالا را به صورت زیر بازنویسی کنیم:

۲ ÷ (محیط چند ضلعی × ارتفاع چند ضلعی) = مساحت چند ضلعی منتظم

فرمول مساحت چندضلعی منتظم

فرمول کلی مساحت چندضلعی منتظم عبارت است از:

$$
A = \frac { ۱ } { ۲ } aP
$$

• A: مساحت چندضلعی منتظم
• a: ارتفاع
• P: محیط

بر اساس فرمول محیط چندضلعی منتظم، فرمول بالا به صورت زیر نیز نوشته می‌شود:

$$
A = \frac { ۱ } { ۲ } a ns
$$

• A: مساحت چندضلعی منتظم
• a: ارتفاع
• n: تعداد ضلع‌ها
• s: طول ضلع

اگر به جای ارتفاع (a)، فرمول آن را قرار دهیم، فرمول بالا به شکل زیر درمی‌آید:

$$
A = \frac { n \times s ^ { ۲ } } { ۲ \tan { \frac { ۱۸۰ ^ { \circ } } { n } } }
$$

به عبارت دیگر، با داشتن تعداد ضلع‌ها و اندازه هر ضلع چندضلعی منتظم، امکان محاسبه مساحت آن فراهم می‌شود. فرمول مساحت چندضلعی منتظم، فرم‌های مختلفی دارد که در مطلب «مساحت چندضلعی منتظم چگونه بدست می‌آید؟ — به زبان ساده + حل مثال»، به طور کامل به آن‌ها پرداخته شده است.

فرمول مساحت مثلث متساوی الاضلاع

مثلث متساوی الاضلاع، یک سه‌ضلعی منتظم است. محاسبه مساحت مثلث، با استفاده از روش‌های مختلفی نظیر رابطه کلی مساحت مثلث‌ها، فرمول هرون و فرمول سینوس انجام می‌گیرد.

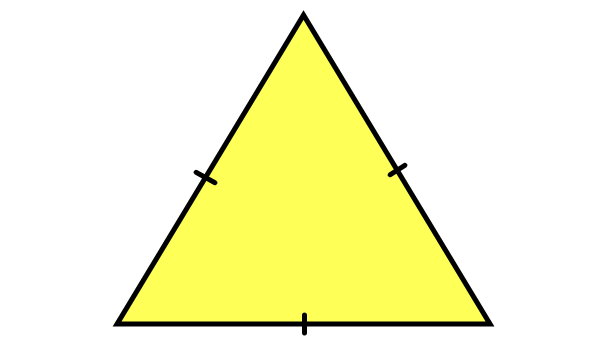
فرمول کلی مساحت مثلث متساوی الاضلاع به صورت زیر نوشته می‌شود:

$$
A = \frac {h \times b } { ۲ }
$$

• A: مساحت مثلث متساوی الاضلاع
• h: اندازه ارتفاع مثلث متساوی الاضلاع
• b: اندازه قاعده یا ضلع مثلث متساوی الاضلاع

این فرمول، همان فرمول محاسبه مساحت چندضلعی منتظم است. البته امکان محاسبه مساحت مثلث متساوی الاضلاع، بدون ارتفاع یا بدون ضلع نیز وجود دارد. در مطلب «مساحت مثلث متساوی الاضلاع — حل تمرین و مثال‌های متنوع» به طور مفصل به این فرمول‌ها پرداخته شده است.

فرمول مساحت مربع

مربع، یک چهارضلعی منتظم با راس‌های قائمه است. مساحت این چندضلعی منتظم از ضرب طول یک ضلع در خودش به دست می‌آید. مساحت مربع، با استفاده از اندازه یکی از قطرهای آن نیز محاسبه می‌شود.

مثلث متساوی الاضلاع و مربع، شناخته شده‌ترین چندضلعی‌های منتظم هستند. به غیر از این دو شکل، مساحت چندضلعی‌های منتظم دیگر، معمولا با استفاده از رابطه کلی محاسبه می‌شود.

مثال ۱۳: محاسبه مساحت چندضلعی منتظم از روی محیط

مساحت یک شش‌ضلعی منتظم به محیط ۴۸/۵ سانتی‌متر و ارتفاع ۷ سانتی‌متر را به دست بیاورید.

فرمول مساحت چندضلعی منتظم بر حسب محیط و ارتفاع به صورت زیر نوشته می‌شود:

$$
A = \frac { ۱ } { ۲ } aP
$$

• A: مساحت چندضلعی منتظم
• a: ارتفاع برابر ۷
• P: محیط برابر ۴۸/۵

$$
A = \frac { ۱ } { ۲ } \times ۷ \times ۴۸/۵
$$

$$
A = ۱۶۹/۷۵
$$

مساحت شش‌ضلعی منتظم برابر با ۱۶۹/۷۵ سانتی‌متر مربع است.

مثال ۱۴: محاسبه مساحت چندضلعی منتظم از روی ضلع

مساحت یک پنج‌ضلعی به ضلع ۵ متر را حساب کنید.

فرمول محاسبه مساحت پننج‌ضلعی منتظم برابر است با:

$$
A = \frac { ۱ } { ۲ } aP
$$

• A: مساحت پنج‌ضلعی منتظم
• a: ارتفاع
• P: محیط

ارتفاع پنج‌ضلعی منتظم، توسط فرمول زیر محاسبه می‌شود:

$$
a = \frac { s } { ۲ \tan { \frac { ۱۸۰ ^ { \circ } } { n } } }
$$

• a: ارتفاع پنج‌ضلعی منتظم
• s: طول ضلع برابر با ۵ متر
• n: تعداد ضلع‌ها برابر با ۵

$$
a = \frac { ۵ } { ۲ \tan { \frac { ۱۸۰ ^ { \circ } } { ۵ } } }
$$

$$
a = \frac { ۵ } { ۲ \tan { ۳۶ ^ { \circ } } }
$$

تانژانت زاویه ۳۶ درجه، حدود ۰/۷۳ است:

$$
a = \frac { ۵ } { ۲ \times ۰/۷۳ }
$$

$$
a = \frac { ۵ } { ۱/۴۶}
$$

$$
a = ۳/۴۲
$$

محیط پنج‌ضلعی منتظم نیز از فرمول زیر به دست می‌آید:

$$
P = n s
$$

• P: محیط پنج‌ضلعی منتظم
• n: تعداد ضلع‌ها برابر با ۵
• s: اندازه هر ضلع برابر با ۵ متر

$$
P = ۵ \ times ۵
$$

$$
P = ۲۵
$$

اکنون، اندازه محیط و ارتفاع را درون فرمول مساحت قرار می‌دهیم:

$$
A = \frac { ۱ } { ۲ } \times ۳/۴۲ \times ۲۵
$$

$$
A \approx ۴۲/۷۵
$$

در نتیجه، مساحت پنج‌ضلعی منتظم برابر با ۴۲/۷۵ متر مربع است.

مرکز تقارن و محور تقارن چند ضلعی منتظم چیست؟

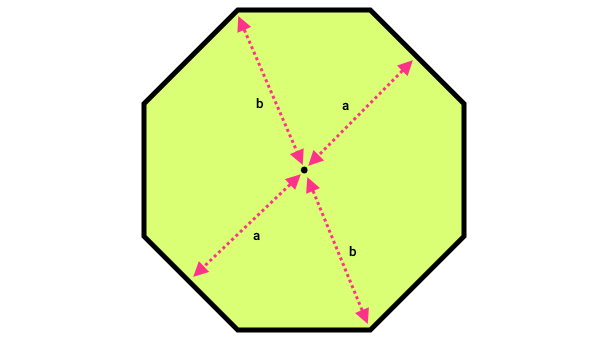
اگر فاصله یک نقطه تا مرکز، با فاصله نقطه مقابل آن تا مرکز برابر باشد، چندضلعی‌های منتظم دارای تقارن مرکزی و مرکز تقارن خواهد بود. این نوع تقارن، در چندضلعی‌های منتظم با تعداد ضلع‌های زوج مشاهده می‌شود (تصویر زیر). البته چندضلعی‌های منتظم با تعداد ضلع‌های فرد، تقارن مرکزی ندارند.

تمام چندضلعی‌های منتظم، دارای تقارن محوری هستند. به عبارت دیگر، در این اشکال هندسی، یک خط فرضی وجود دارد که آن‌ها را به دو قسمت کاملا مساوی تقسیم می‌کند. به این خط، محور تقارن می‌گویند. در صورت تا زدن چندضلعی‌های منتظم حل محور تقارن‌شان، دو نیمه شکل بر روی هم منطبق می‌شوند.

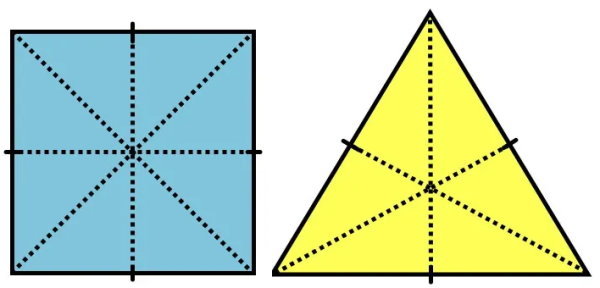
هر n ضلعی منتظم، n محور تقارن دارد. محورهای تقارن فرد ضلعی منتظم (مانند مثلث بالا)، از اتصال هر راس به میانه ضلع مقابل آن راس ایجاد می‌شوند. محورهای تقارن زوج ضلعی منتظم (مانند مربع بالا)، قطرها و عمود منصف‌های اضلاع هستند.

تقارن چرخشی چندضلعی منتظم

علاوه بر تقارن مرکزی در زوج ضلعی‌های منتظم و تقارن محوری در فرد/زوج چندضلعی‌های منتظم، تمام چندضلعی‌های منتظم، تقارن چرخشی دارند. با دوران چندضلعی‌های منتظم حول مرکزشان، شکل آن‌ها چندین بار به حالت اولیه خود باز می‌گردد. به عنوان مثال، مثلث متساوی الاضلاع، دارای تقارن چرخشی مرتبه سه است. تصویر متحرک زیر، این نوع تقارن را به خوبی نمایش می‌دهد.

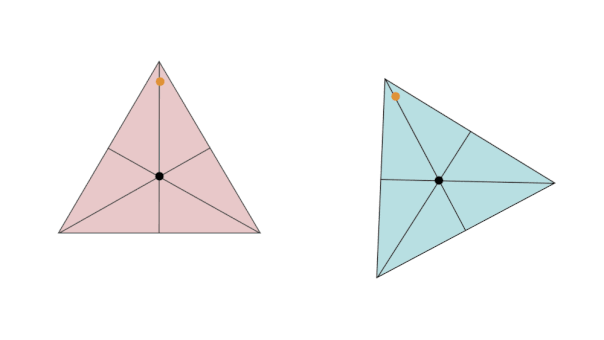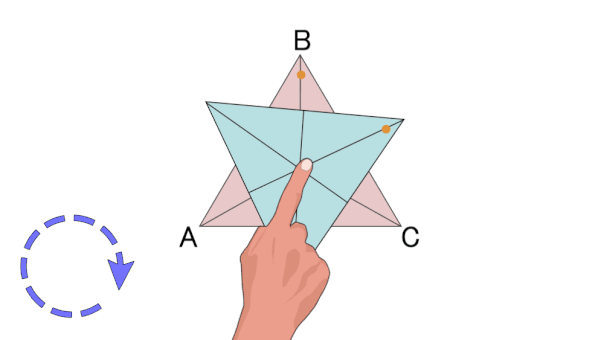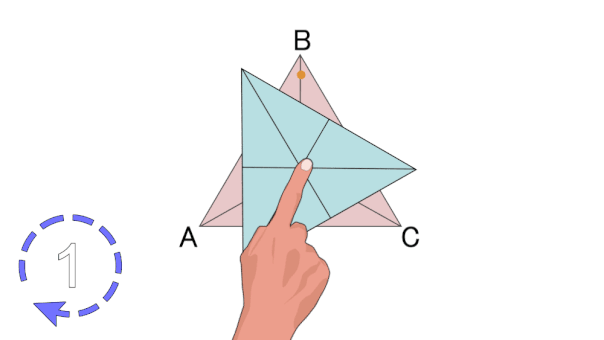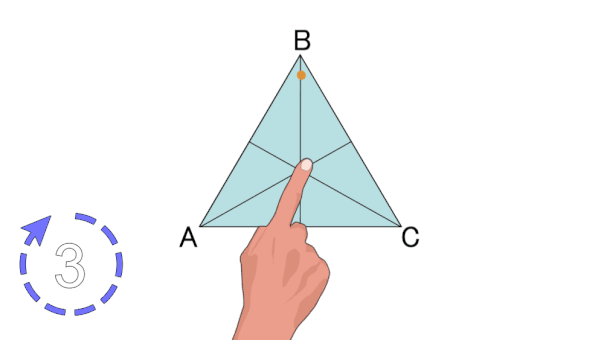
در صورت علاقه به یادگیری بیشتر در مورد حالت‌های تقارن چندضلعی‌های منتظم، مطالعه مطلب «محور تقارن چند ضلعی منتظم چیست؟ — به زبان ساده» را به شما پیشنهاد می‌کنیم.

چند ضلعی منتظم ستاره ای چیست ؟

چندضلعی ستاره‌ای، یکی از حالت خاص چندضلعی منتظم است. تمام چندضلعی‌های منتظم، محدب هستند. به علاوه، در چندضلعی‌ها، هیچ‌یک از ضلع‌ها همدیگر را قطع نمی‌کنند. شکل‌های ستاره‌ای، به عنوان چندضلعی‌های منتظم غیر محدب با ضلع‌های متقاطع شناخته می‌شوند.

سوالات متداول در رابطه با چند ضلعی منتظم

در این بخش، به برخی از سوالات پرتکرار در رابطه با چندضلعی‌های منتظم به طور خلاصه پاسخ می‌دهیم.

تعریف چند ضلعی منتظم چیست ؟

به چندضلعی دارای زاویه‌های هم‌اندازه و ضلع‌های مساوی، چندضلعی منتظم می‌گویند.

به چند ضلعی که همه اضلاع و زاویه هایش برابر باشند چه می‌گویند ؟

چندضلعی منتظم.

آیا مربع چند ضلعی منتظم است ؟

بله. مربع، با چهار ضلع برابر و چهار زاویه ۹۰ درجه، یکی از انواع چندضلعی‌های منتظم در نظر گرفته می‌شود.

آیا مستطیل چند ضلعی منتظم است ؟

خیر. با وجود زاویه‌های برابر (۹۰ درجه)، ضلع‌های مستطیل با هم مساوی نیستند.

آیا متوازی الاضلاع چند ضلعی منتظم است ؟

خیر. در حالت کلی، امکان متفاوت بودن اندازه زاویه‌ها و ضلع‌های متوازی‌الاضلاع وجود دارد.

آیا لوزی چند ضلعی منتظم است ؟

خیر. با وجود ضلع‌های برابر، تمام زاویه‌های لوزی هم‌اندازه نیستند.

آیا دایره چند ضلعی منتظم است ؟

خیر. دایره، یک منحنی بسته است و در گروه چندضلعی‌ها قرار نمی‌گیرد.

چند ضلعی منتظم محدب است یا مقعر؟

تمام چندضلعی‌های منتظم، محدب هستند.

آیا چند ضلعی منتظم مقعر وجود دارد ؟

خیر. چند ضلعی مقعر باید حداقل یک زاویه بزرگ‌تر از ۱۸۰ درجه داشته باشد.

آیا ستاره چند ضلعی منتظم است ؟

خیر. البته برخی از شکل‌های ستاره‌ای با ضلع‌های متقاطع، با عنوان ستاره‌های منتظم غیر محدب شناخته می‌شوند.

چند ضلعی منتظم چند قطر دارد؟

یک n ضلعی منتظم، ۲÷(۳-n)n قطر دارد.

آیا چند ضلعی منتظم محور تقارن دارد ؟

بله. تمام چندضلعی‌های مقعر، دارای محور تقارن هستند.

تعداد محور تقارن چند ضلعی منتظم چند است؟

تعداد محور تقارن یک n ضلعی منتظم، برابر با n است.

آیا چند ضلعی منتظم مرکز تقارن دارد ؟

بله و خیر. در صورت زوج بودن تعداد ضلع‌ها، چندضلعی منتظم دارای مرکز تقارن است. یک چند ضلعی منتظم با تعداد ضلع‌های فرد، نمی‌تواند مرکز تقارن داشته باشد.

کوچکترین چند ضلعی منتظم چیست ؟

مثلث متساوی الاضلاع، کوچک‌ترین چندضلعی منتظم از نظر تعداد ضلع‌ها است.