نمونه سوال مساحت متوازی الاضلاع با جواب — حل تمرین های متنوع

متوازی‌الاضلاع، یک چهارضلعی است که ضلع‌های مقابل آن، هم‌‌اندازه و موازی هستند. فرمول‌های مختلفی برای محاسبه اندازه مساحت متوازی‌الاضلاع وجود دارند. در این فرمول‌ها، معمولا از ارتفاع، قاعده، قطر، ضلع یا زاویه استفاده می‌شود. در این مطلب، قصد داریم چندین نمونه سوال مساحت متوازی الاضلاع با جواب را مورد بررسی قرار دهیم. مطالعه این نمونه سوال‌ها می‌توانند به شما در تسلط بر محاسبه مساحت متوازی‌الاضلاع و آمادگی برای آزمون‌های مختلف کمک کنند.

نمونه سوال مساحت متوازی الاضلاع با قاعده و ارتفاع

در این بخش، چند نمونه سوال مساحت متوازی الاضلاع با قاعده و ارتفاع را حل می‌کنیم. فرمول مساحت متوازی الاضلاع با قاعده و ارتفاع برابر است با:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

عبارت جبری این فرمول به صورت زیر نوشته می‌شود:

$$
S= bh
$$

سوال 1

مساحت شکل زیر به دست آورید. (اندازه‌های نمایش داده شده به سانتی‌متر هستند.)

شکل بالا، متوازی‌الاضلاعی به قاعده 8 سانتی‌متر و ارتفاع 4 سانتی‌متر را نمایش می‌دهد. بر اساس فرمول مساحت متوازی‌الاضلاع داریم:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

اندازه ارتفاع و قاعده را درون فرمول قرار می‌دهیم و آن‌ها را در هم ضرب می‌کنیم:

۴ × ۸ = مساحت متوازی‌الاضلاع

32 = مساحت متوازی‌الاضلاع

در نتیجه، مساحت متوازی‌الاضلاع برابر ۳۲ سانتی‌متر مربع است.

سوال 2

مساحت کدام شکل بیشتر است؟

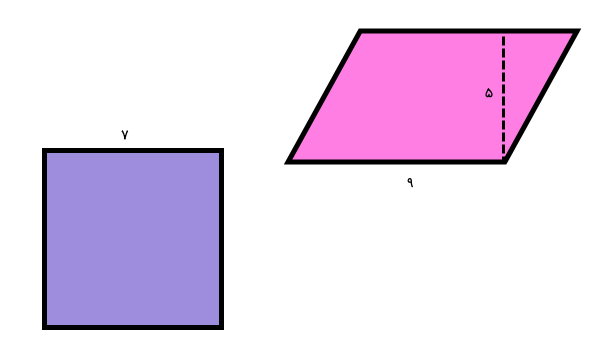
در تصویر بالا، یک مربع و یک متوازی الاضلاع را نمایش می‌دهد. مساحت مربع از ضرب یک ضلع در خودش به دست می‌آید:

خودش × اندازه ضلع = مساحت مربع

۷ × ۷ = مساحت مربع

۴۹ = مساحت مربع

مساحت متوازی الاضلاع برابر است با:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

۵ × ۹ = مساحت متوازی‌الاضلاع

۴۵ = مساحت متوازی‌الاضلاع

در این سوال، مساحت مربع بیشتر است.

سوال ۳

مساحت شکل زیر چند است؟ (اندازه‌های نمایش داده شده به میلی‌متر هستند.)

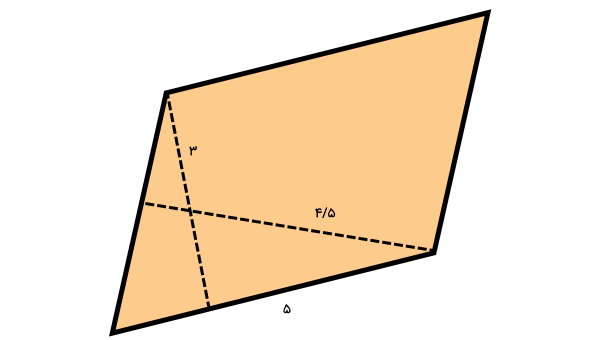
اندازه یک ضلع و دو ارتفاع متوازی‌الاضلاع را داریم. مساحت متوازی‌الاضلاع، با ضرب قاعده در ارتفاع نظیر محاسبه می‌شود. بر اساس شکل بالا، ارتفاع نظیر قاعده 5 میلی‌متری برابر 3 میلی‌متر است. بنابراین، مساحت متوازی‌الاضلاع از رابطه زیر به دست می‌آید:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

۳ × ۵ = مساحت متوازی‌الاضلاع

۱۵ = مساحت متوازی‌الاضلاع

در نتیجه، مساحت متوازی‌الاضلاع برابر 15 میلی‌متر مربع است.

سوال 4

مساحت متوازی‌الاضلاع زیر را به دست بیاورید.

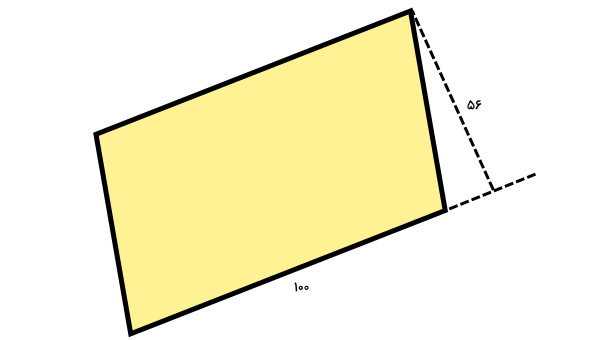
خط‌چین نمایش داده شده در تصویر بالا بر راستای ضلع پایینی متوازی‌الاضلاع عمود شده است. بنابراین، اندازه این خط‌چین، ارتفاع نظیر قاعده را نمایش می‌دهد. به این ترتیب، مساحت متوازی‌الاضلاع برابر است با:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

56 × 100 = مساحت متوازی‌الاضلاع

5600 = مساحت متوازی‌الاضلاع

سوال 5

مساحت قسمت رنگی متوازی‌الاضلاع زیر را بدست بیاورید.

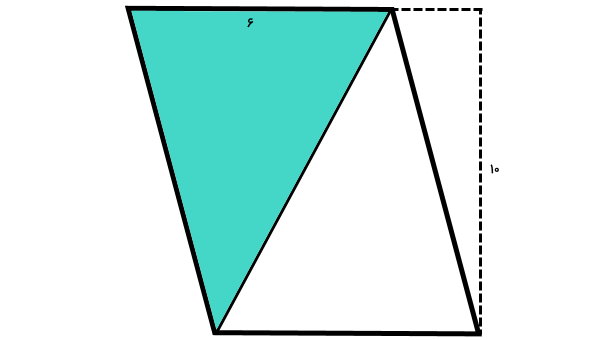
در شکل بالا، یکی از قطرهای متوازی‌الاضلاع رسم شده است. این قطر، متوازی‌الاضلاع را به دو مثلث هم‌اندازه (هم‌نهشت) تقسیم می‌کند. بنابراین، اگر مساحت کل متوازی‌الاضلاع را تقسیم بر دو کنیم، مساحت قسمت رنگی به دست می‌آید. مساحت متوازی‌الاضلاع برابر است با:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

۶ × ۱۰ = مساحت متوازی‌الاضلاع

60 = مساحت متوازی‌الاضلاع

مساحت قسمت رنگی نیز به صورت زیر محاسبه می‌شود:

۲ ÷ مساحت متوازی‌الاضلاع = مساحت قسمت رنگی

۲ ÷ ۶۰ = مساحت قسمت رنگی

۳۰ = مساحت قسمت رنگی

اگر به تصویر بالا دقت کنید، متوجه خواهید شد که قاعده و ارتفاع متوازی‌الاضلاع، همان قاعده و ارتفاع مثلث مورد نظر است. مساحت مثلث، از رابطه «قاعده ضربدر ارتفاع تقسیم دو» به دست می‌آید. بنابراین، می‌توانستیم این سوال را بدون استفاده از فرمول مساحت متوازی‌الاضلاع و تنها توسط فرمول مساحت مثلث حل کنیم.

سوال 6

از یک راس متوازی‌الاضلاع، پاره‌خطی را به مرکز قاعده آن رسم کرده‌ایم. با توجه به اطلاعات موجود، مساحت قسمت رنگی را تعیین کنید.

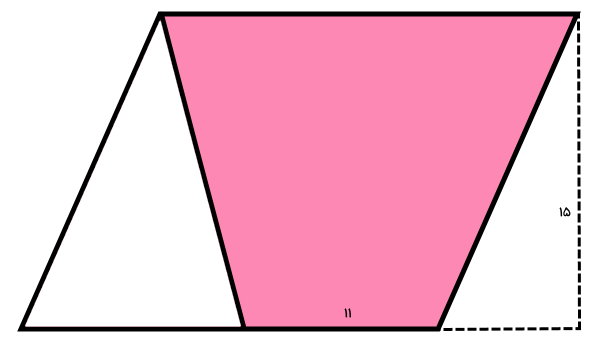
این سوال، تا حدی به سوال 5 شباهت دارد. برای به دست آوردن مساحت قسمت رنگی، می‌توانیم از دو روش استفاده کنیم. در روش اول، مساحت قسمت رنگی، از اختلاف مساحت متوازی‌الاضلاع با بخش سفید به دست می‌آید:

مساحت سفید - مساحت متوازی‌الاضلاع = مساحت رنگی

بر اساس فرمول مساحت متوازی‌الاضلاع، داریم:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

با توجه اطلاعات مسئله و شکل، قاعده متوازی‌الاضلاع برابر 22 است:

۱۵ × 22 = مساحت متوازی‌الاضلاع

۳۳۰ = مساحت متوازی‌الاضلاع

پاره خط درون متوازی‌الاضلاع، به مرکز قاعده برخورد کرده است. بنابراین، قسمت سفید رنگ، مثلثی به ارتفاع 15 و قاعده ۱۱ است. مساحت این مثلث با استفاده از رابطه زیر محاسبه می‌شود:

۲ ÷ (ارتفاع × قاعده) = مساحت مثلث

۲ ÷ (۱۵ × ۱۱) = مساحت مثلث

۲ ÷ (۱۶۵) = مساحت مثلث

82/5 = مساحت مثلث

در نتیجه:

مساحت سفید - مساحت متوازی‌الاضلاع = مساحت رنگی

82/5 - 330 = مساحت رنگی

247/5 = مساحت رنگی

مساحت قسمت رنگی برابر 247/5 واحد سطح است. به منظور محاسبه این مساحت، یک روش دیگر نیز وجود دارد. قسمت رنگی، به شکل یک ذوزنقه است. مساحت ذوزنقه با استفاده از رابطه زیر محاسبه می‌شود:

ارتفاع × نصف مجموع دو قاعده = مساحت ذوزنقه

ارتفاع ذوزنقه برابر 15 و قاعده‌های آن برابر 11 و 22 است. بنابراین، داریم:

۱۵ × [۲ ÷ (۱۱ + ۲۲)] = مساحت ذوزنقه

۱۵ × (۲ ÷ ۳۳) = مساحت ذوزنقه

۱۵ × 16/5 = مساحت ذوزنقه

247/5 = مساحت ذوزنقه

همان‌طور که مشاهده می‌کنید. نتیجه مساحت قسمت رنگی در هر دو روش برابر است.

نمونه سوال مساحت متوازی الاضلاع اعشاری

در بخش قبلی، چند نمونه سوال مساحت متوازی الاضلاع را مورد بررسی قرار دادیم. در تمام این مثال‌ها، اندازه ارتفاع و قاعده به صورت اعداد طبیعی بیان شدند. البته در سوال 6، بخشی از محاسبات به صورت اعشاری بود. در این بخش، حل نمونه سوال مساحت متوازی الاضلاع را با اعداد اعشاری ادامه می‌دهیم.

سوال 7

مساحت متوازی‌الاضلاع زیر را حساب کنید. (اعداد بر حسب متر هستند.)

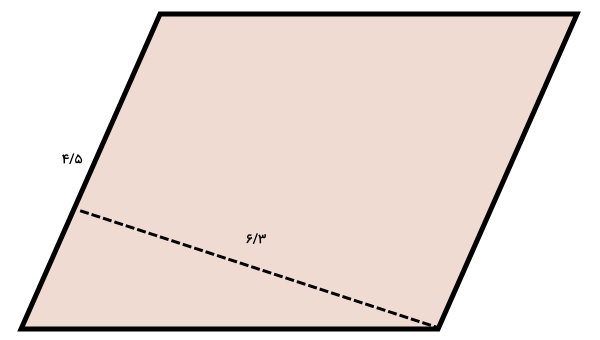
اندازه قاعده و ارتفاع نظیر متوازی‌الاضلاع (4/5 و 6/3 سانتی‌متر)، به صورت اعشاری هستند. از این‌رو، محاسبه مساحت با استفاده از اصول ضرب اعشاری انجام می‌گیرد. مطابق با فرمول مساحت متوازی‌الاضلاع، داریم:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

6/3 × 4/5 = مساحت متوازی‌الاضلاع

برای حل ضرب بالا، دو روش وجود دارد. در روش اول، می‌توانیم اندازه‌های ارتفاع و قاعده را بدون در نظر گرفتن اعشار، در یکدیگر ضرب کنیم. سپس، مجموع تعداد رقم‌های بعد از اعشار این دو اندازه را به عنوان تعداد رقم‌های اعشار حاصل‌ضرب قرار دهیم.

در روش دوم، اندازه‌های ارتفاع و قاعده را به شکل کسر ساده در می‌آوریم و سپس آن‌ها در یکدیگر ضرب می‌کنیم. در انتها، جواب نهایی را به صورت اعشاری می‌نویسیم. در هر حال، نتیجه مساحت متوازی‌الاضلاع مورد سوال برابر می‌شود با:

28/35 = مساحت متوازی‌الاضلاع

در نتیجه، مساحت متوازی‌الاضلاع برابر 28/35 متر مربع است.

سوال 8

مساحت متوازی‌الاضلاع زیر را به روش ضرب اعشاری

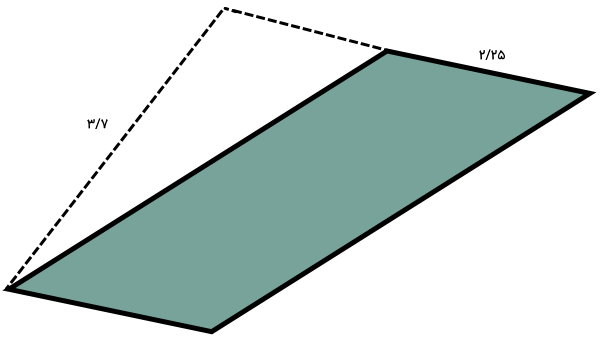
مساحت متوازی‌لاضلاع بالا برابر است با:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

۳/۷ × ۲/۲۵ = مساحت متوازی‌الاضلاع

به منظور انجام محاسبات، ابتدا اعداد را بدون در نظر گرفتن اعشار در یکدیگر ضرب می‌کنیم:

8325 = ۳۷ × ۲۲۵

عدد 2/25، دارای دو رقم اعشار و عدد 3/7، دارای یک رقم اعشار است. این دو عدد در مجموع، سه رقم اعشار دارند. بنابراین، حاصل‌ضرب بالا باید سه رقم اعشار داشته باشد:

8/325 = ۳/۷ × ۲/۲۵

در نتیجه:

8/325 = مساحت متوازی‌الاضلاع

مساحت متوازی‌الاضلاع برابر 8/325 واحد سطح است.

سوال 9

مساحت متوازی‌الاضلاع زیر را به صورت کسر ساده محاسبه کنید.

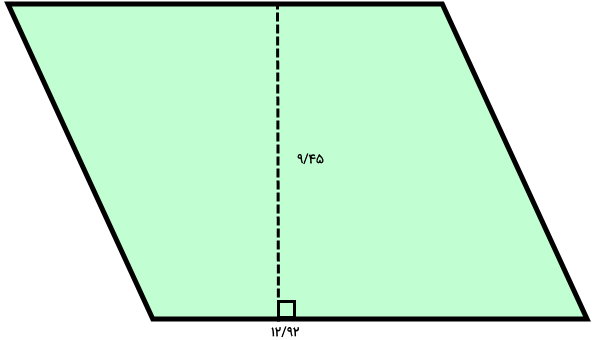
مساحت متوازی‌الاضلاع از رابطه زیر به دست می‌آید:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

9/45 × 12/92 = مساحت متوازی‌الاضلاع

حاصل‌ضرب اعداد بالا بدون اعشار برابر است با:

122094۰ = 945 × 1292

دو عدد ضرب شده، در مجموع، چهار رقم بعد از اعشار دارند. بنابراین، داریم:

122/094۰ = 9/45 × 12/92

در نتیجه:

122/094 = مساحت متوازی‌الاضلاع

اگر آخرین رقم اعشار برابر صفر باشد، می‌توانیم آن را حذف کنیم. برای نمایش مساحت اعشاری بالا به صورت کسری، تعداد رقم‌های بعد از اعشار را می‌شماریم. این مساحت، سه رقم بعد از اعشار دارد. بنابراین، شکل کسری آن به صورت زیر خواهد بود:

$$
\frac {۱۲۲۰۹۴}{۱۰۰۰}
$$

نمونه سوال مساحت متوازی الاضلاع کسری

در بخش قبلی، با حل چند نمونه سوال مساحت متوازی الاضلاع اعشاری آشنا شدید. اعشار، یکی از روش‌های نمایش اعداد کسری است. اعداد کسری، با استفاده کسر ساده یا مخلوط نیز نمایش داده می‌شوند. در این بخش، چند نمونه سوال مساحت متوازی الاضلاع کسری را حل می‌کنیم.

سوال 10

مساحت متوازی‌الاضلاع زیر چند است؟ (اعداد بر حسب سانتی‌متر هستند.)

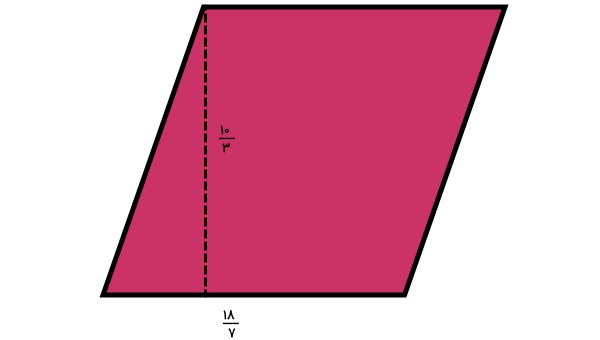
مساحت متوازی‌الاضلاع با اندازه‌های کسری به صورت زیر محاسبه می‌شود:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

$$
= \frac {۱۰}{۳} \times \frac {۱۸}{۷}
$$

به منظور ضرب کسرهای ساده، صورت کسرها را در یکدیگر و مخرج آن‌ها را در یگدیگر ضرب می‌کنیم:

$$
= \frac {۱۰ \times ۱۸}{۳ \times ۷}
$$

$$
= \frac {۱۸۰}{۲۱}
$$

در نتیجه، مساحت متوازی‌الاضلاع برابر با کسر بالا (صد و هشتاد بیست و یکم) است. البته صورت مخرج کسر بالا بر عدد 3 بخش‌پذیر هستند. بنابراین می‌توانیم آن را به صورت زیر ساده کنیم:

$$
= \frac {۶۰}{۷}
$$

سوال 11

مساحت شکل زیر را به صورت کسری محاسبه کنید.

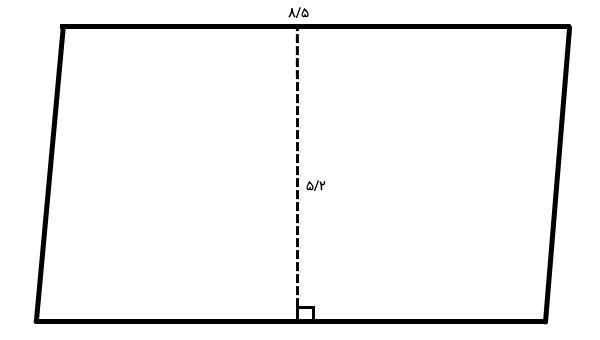
اندازه قاعده و ارتفاع متوازی‌الاضلاع به صورت اعشاری بیان شده‌اند. با این وجود، صورت مسئله، مساحت کسری را از ما می‌خواهد. بنابراین، برای حل مسئله، ابتدا این اعداد را به فرم کسر متعارفی در می‌آوریم:

$$
۸/۵ = \frac {۸۵}{۱۰}
$$

$$
۵/۲ = \frac {۵۲}{۱۰}
$$

اکنون این اعداد را درون فرمول مساحت متوازی‌الاضلاع قرار می‌دهیم:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

$$
= \frac {۸۵}{۱۰} \times \frac {۵۲}{۱۰}
$$

$$
= \frac {۴۴۲۰}{۱۰۰}
$$

در نتیجه، مساحت متوازی‌الاضلاع چهار هزار و چهار صد و بیست صدم است. فرم اعشاری این عدد به صورت 44/2 نمایش داده می‌شود.

سوال 12

مساحت متوازی‌الاضلاع زیر را به دست بیاورید. (اعداد بر حسب اینچ هستند.)

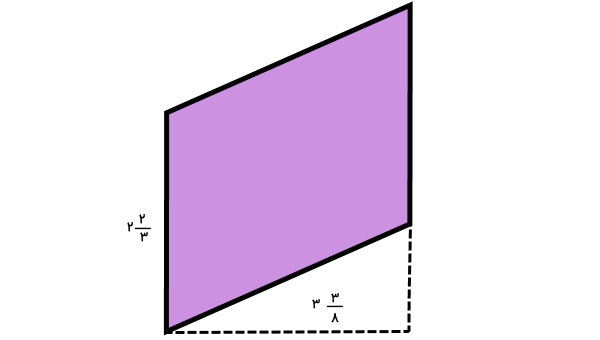
اندازه قاعده و ارتفاع متوازی‌الاضلاع بالا، به صورت عدد مخلوط بیان شده‌اند. اعداد مخلوط، یکی از انواع کسرها هستند. به منظور انجام محاسبات، ابتدا این اعدا را به شکل کسر ساده در می‌آوریم:

$$
۲ \frac {۲}{۳}= \frac {(۲ \times ۳) + ۲}{۳} = \frac {۸}{۳}
$$

$$
۳ \frac {۳}{۸}= \frac {(۳ \times ۸) + ۳}{۸} = \frac {۲۷}{۸}
$$

اکنون می‌توانیم این اعداد را درون فرمول مساحت متوازی‌الاضلاع قرار دهیم:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

$$
= \frac {۸}{۳} \times \frac {۲۷}{۸}
$$

$$
= ۹
$$

در نتیجه، مساحت متوازی‌الاضلاع برابر 9 اینچ مربع است.

نمونه سوال مساحت متوازی الاضلاع با تبدیل واحد

در برخی از موارد، اندازه‌های معلوم در مسئله بر اساس یک واحد خاص داده شده اما جواب مسئله بر اساس یک واحد متفاوت خواسته می‌شود. در این شرایط، ابتدا باید اندازه‌ها را به واحد مورد نظر تبدیل کرد و سپس محاسبات را انجام داد. برای یادگیری نحوه حل این مسائل، چند نمونه سوال مساحت متوازی الاضلاع با تبدیل واحد را مورد بررسی قرار می‌دهیم.

سوال 13

مساحت متوازی‌الاضلاع زیر را بر حسب متر مربع حساب کنید. (اعداد نمایش داده شده بر حسب سانتی‌متر هستند.)

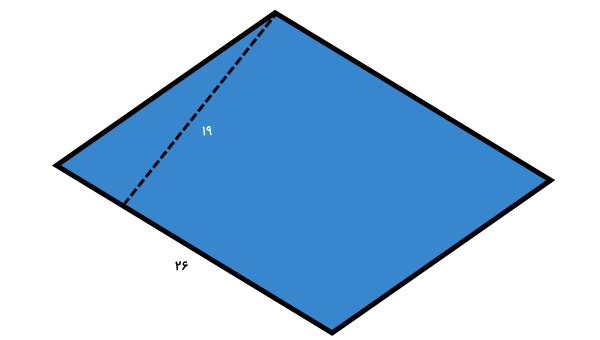
ارتفاع و قاعده متوازی‌الاضلاع، به ترتیب برابر 19 و 26 سانتی‌متر هستند. اندازه مساحت بر حسب متر مربع خواسته شده است. بنابراین، ابتدا باید اندازه‌های معلوم را از واحد سانتی‌متر به واحد متر تبدیل کنیم. این کار، با تقسیم اعداد بر عدد 100 انجام می‌شود:

$$
۱۹ cm = \frac{۱۹}{۱۰۰} m
$$

$$
۲۶ cm = \frac{۲۶}{۱۰۰} m
$$

اعداد بالا را درون فرمول مساحت متوازی‌الاضلاع قرار می‌دهیم:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

$$
= \frac {۸۵}{۱۰} \times \frac {۵۲}{۱۰}
$$

$$
= \frac {۱۹}{۱۰۰} \times \frac {۲۶}{۱۰۰}
$$

$$
= \frac {۴۹۴}{۱۰۰۰۰}
$$

به این ترتیب، اندازه مساحت بر حسب متر مربع به دست می‌آید. می‌توانیم کسر بالا را به صورت عدد اعشاری ۰/۰۴۹۴ متر مربع نیز نمایش دهیم.

سوال 14

اندازه قاعده و ارتفاع متوازی‌الاضلاع زیر با دو واحد متفاوت بیان شده است. مساحت متوازی‌الاضلاع را بر حسب سانتی‌متر مربع به دست بیاورید.

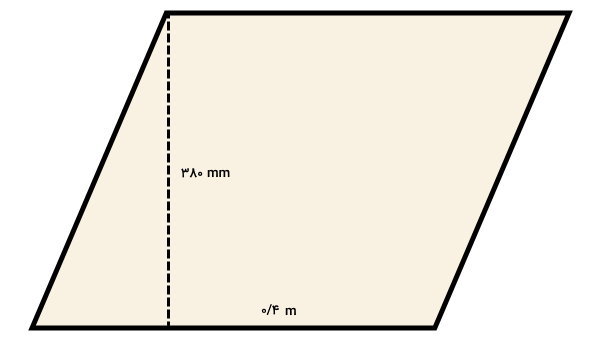
یکی از اندازه‌های بالا بر حسب میلی‌متر و اندازه دیگر بر متر داده شده‌اند. صورت سوال، مساحت را بر حسب سانتی‌متر مربع می‌خواهد. بنابراین، باید ابتدا تبدیل واحد اندازه‌های معلوم به سانتی‌متر را انجام دهیم. به این ترتیب داریم:

$$
۳۸۰ mm= ۳۸ cm
$$

$$
۰/۴ m= ۴۰ cm
$$

هر دو اندازه را بر حسب سانتی‌متر نوشتیم. این اندازه‌ها را درون فرمول مساحت متوازی‌الاضلاع قرار می‌دهیم:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

۳۸ × ۴۰ = مساحت متوازی‌الاضلاع

1520 = مساحت متوازی‌الاضلاع

در نتیجه، مساحت متوازی‌الاضلاع برابر 1520 سانتی‌متر مربع است.

سوال 15

مساحت متوازی‌الاضلاع به قاعده 9/5 سانتی‌متر و ارتفاع 6 سانتی‌متر، چند اینچ مربع است؟

هر اینچ، 2/54 سانتی‌متر است. به این ترتیب می‌توانیم اندازه‌ها را از سانتی‌متر به اینچ تبدیل کنیم. برای این کار، معمولا از نسبت زیر استفاده می‌شود:

$$
\frac {۱in}{۲/۵ cm} = \frac {? \space in}{? \space cm}
$$

بر اساس نسبت بالا داریم:

$$
۹/۵ cm =۳/۷۴in
$$

$$
۶ cm =۲/۳۶ in
$$

با قرار دادن اندازه‌های بالا در فرمول مساحت متوازی‌الاضلاع، اندازه مساحت بر حسب اینچ مربع به دست می‌آید:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

۲/۳۶ × ۳/۷۴ = مساحت متوازی‌الاضلاع

8/83 = مساحت متوازی‌الاضلاع

در نتیجه، مساحت متوازی‌الاضلاع برابر 8/83 اینچ مربع است.

نمونه سوال تعیین قاعده با مساحت متوازی الاضلاع

در این بخش، چند نمونه سوال مساحت متوازی الاضلاع را با هدف پیدا کردن اندازه قاعده حل می‌کنیم.

سوال 1۶

مساحت متوازی‌الاضلاع زیر برابر 72 متر مربع است. قاعده نظیر ارتفاع مشخص شده را تعیین کنید.

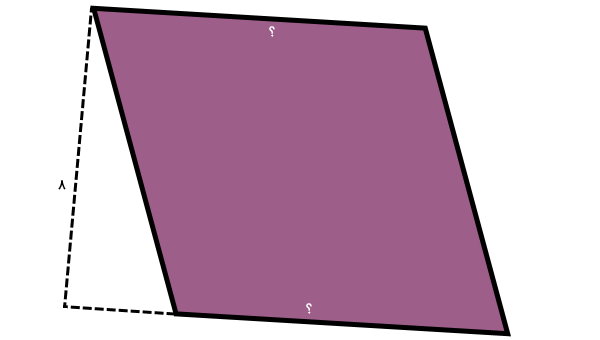
ضلع‌های مشخص شده با علامت سوال، قاعده‌های نظیر ارتفاع معلوم هستند. با قرار دادن اندازه مساحت و ارتفاع در فرمول زیر، اندازه این ضلع‌ها به دست می‌آید:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

۸ × قاعده = ۷۲

۸ ÷ ۷۲ = قاعده

۹ = قاعده

سوال 17

مساحت متوازی‌الاضلاعی برابر 35 سانتی‌متر مربع است. اگر اندازه یکی از ارتفاع‌های این متوازی‌الاضلاع برابر 7 سانتی‌متر و اندازه ارتفاع دیگر آن برابر 5 سانتی‌متر باشد، اندازه قاعده‌های نظیر هر ارتفاع چقدر خواهد بود؟ متوازی‌الاضلاع مورد سوال، کدام یک از اشکال هندسی است؟

بر اساس اطلاعات مسئله، قاعده نظیر ارتفاع 7 سانتی‌متری (قاعده اول) برابر است با:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

۷ × قاعده اول = 35

۷ ÷ ۳۵ = قاعده اول

۵ = قاعده اول

قاعده نظیر ارتفاع 5 سانتی‌متری نیز از رابطه زیر به دست می‌آید:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

۵ × قاعده دوم = 35

۵ ÷ ۳۵ = قاعده دوم

۷ = قاعده دوم

قاعده‌های نظیر دو ارتفاع 7 و 5 سانتی‌متری، به ترتیب برابر 5 و 7 سانتی‌متر هستند. این حالت، در یکی از انواع خاص متوازی‌الاضلاع، به نام مستطیل رخ می‌دهد.

سوال 18

اندازه ضلع مجهول را به دست بیاورید. (اعداد بر حسب سانتی‌متر هستند.)

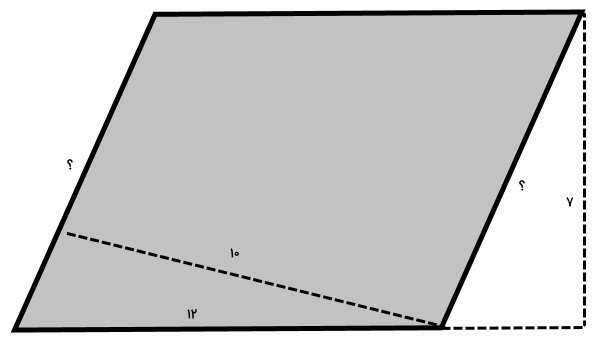
در شکل بالا، قاعده نظیر ارتفاع 10 سانتی‌متری مجهول است. برای به دست آوردن این قاعده، به مساحت متوازی‌الاضلاع نیاز داریم. با توجه به معلوم بودن اندازه قاعده دیگر و ارتفاع نظیر آن، امکان محاسبه مساحت به صورت زیر وجود دارد:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

7 × 12 = مساحت متوازی‌الاضلاع

84 = مساحت متوازی‌الاضلاع

مساحت متوازی‌الاضلاع برابر 84 سانتی‌متر مربع است. این عدد را این بار به همراه ارتفاع 10 سانتی‌متری درون فرمول قرار می‌دهیم تا قاعده مجهول به دست آید:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

10 × قاعده = 84

10 ÷ 84 = قاعده

8/4 = قاعده

در نتیجه، اندازه ضلع یا قاعده مجهول برابر 8/4 سانتی‌متر است.

در ادامه، یک سوال دیگر را با هدف پیدا کردن اندازه ارتفاع مورد بررسی قرار می‌دهیم. روند محاسبه ارتفاع متوازی‌الاضلاع، مشابه روند محاسبه قاعده در سوال‌های 16 تا 18 است.

سوال 19

اندازه ارتفاع دیگر متوازی‌الاضلاع زیر را به دست بیاورید.

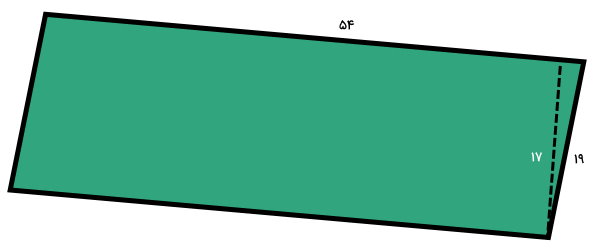
در شکل بالا، اندازه دو ضلع و یک ارتفاع داده شده است. با استفاده از یک ضلع و ارتفاع نظیر آن می‌توانیم مساحت متوازی‌الاضلاع را حساب کنیم:

قاعده × ارتفاع = مساحت متوازی‌الاضلاع

۵۴ × ۱۷ = مساحت متوازی‌الاضلاع

918 = مساحت متوازی‌الاضلاع

اکنون، اندازه مساحت و قاعده دیگر را درون رابطه مساحت قرار می‌دهیم تا ارتفاع نظیر آن قاعده به دست بیاید:

قاعده × ارتفاع = مساحت متوازی‌الاضلاع

19 × ارتفاع = 918

19 ÷ 918 = ارتفاع

48/32 = ارتفاع

نمونه سوال مساحت متوازی الاضلاع با متغیر

در بخش‌های قبلی، چندین نمونه سوال مساحت متوازی الاضلاع را با فرض دانستن مقادیر عددی حل کردیم. در برخی از موارد، اندازه‌های متوازی‌الاضلاع به صورت جبری و متغیر داده می‌شوند. در این بخش، سه نمونه سوال مساحت متوازی الاضلاع با متغیر را مورد بررسی قرار می‌دهیم.

سوال 20

مساحت متوازی‌الاضلاع زیر را بر حسب x به دست بیاورید.

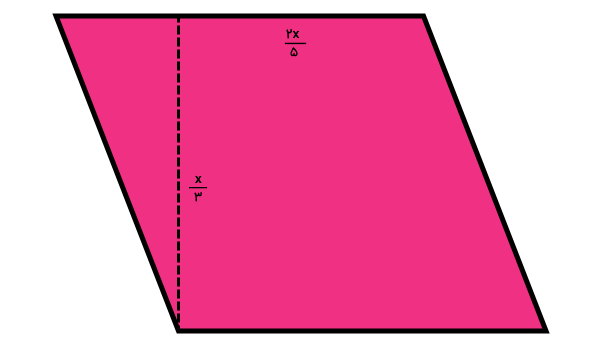
روند محاسبه مساحت متوازی‌الاضلاعی با اندازه‌های متغیر، تفاوتی با مسائل دیگر ندارد. در اینجا نیز فرمول مساحت را نوشته و هر اندازه را درون آن قرار می‌دهیم:

قاعده × ارتفاع = مساحت متوازی‌الاضلاع

$$
= \frac {x}{۳} \times \frac {۲x}{۵}
$$

$$
= \frac {x \times ۲x}{۳ \times ۵}
$$

$$
= \frac {۲x^۲}{۱۵}
$$

به این ترتیب، مساحت متوازی‌الاضلاع بر حسب x به دست می‌آید. اگر مقادیر عددی متغیر x را داشته باشیم، می‌توانیم مقادیر مساحت در x های مختلف را حساب کنیم.

سوال 21

رابطه مساحت متوازی‌الاضلاع زیر را تعیین کنید.

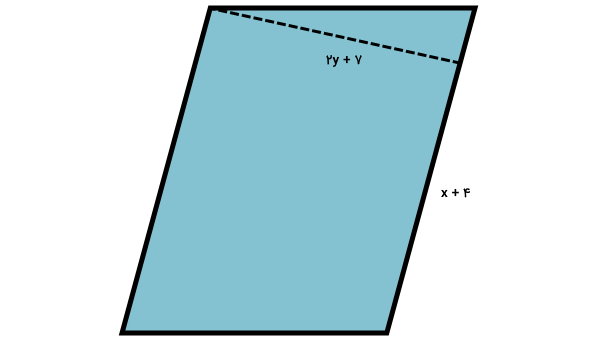
اندازه‌های متوازی‌الاضلاع، به صورت چندجمله‌ای و بر حسب دو متغیر x و y نمایش داده شده‌اند. این اندازه‌ها را درون فرمول مساحت قرار می‌دهیم:

قاعده × ارتفاع = مساحت متوازی‌الاضلاع

$$
= (۲y + ۷) \times (x + ۴)
$$

بر اساس قواعد ضرب چندجمله‌ای داریم:

$$
= ۲yx + ۸y + ۷x + ۲۸
$$

عبارت جبری بالا، رابطه مساحت متوازی‌الاضلاع مورد سوال بر حسب متغیرهای x و y است.

سوال 22

اندازه قاعده و ارتفاع نظیر یک متوازی‌الاضلاع به صورت زیر است. فرمول مساحت متوازی‌الاضلاع را بر حسب x و y به دست بیاورید. اگر x برابر 2 سانتی‌متر و y برابر 3 سانتی‌متر باشد، مساحت متوازی‌الاضلاع چقدر است؟

$$
\frac {۵x}{۲} - ۱
$$

$$
\frac {xy}{۶} + ۳
$$

برای شروع، فرمول مساحت متوازی‌الاضلاع را می‌نویسیم و عبارت‌های بالا را درون آن قرار می‌دهیم:

قاعده × ارتفاع = مساحت متوازی‌الاضلاع

$$
= (\frac {۵x}{۲} - ۱) \times (\frac {xy}{۶} + ۳)
$$

با استفاده از ضرب چندجمله‌ای‌ها، حاصل‌ضرب بالا را به دست می‌آوریم:

$$
=\frac{۵x^۲y} {۱۲}+\frac {۱۵x}{۲}-\frac{xy} {۶}-۳
$$

عبارت جبری بالا، فرمول مساحت متوازی‌الاضلاع مورد سوال بر حسب x و y است. با استفاده از مخرج مشترک و فاکتورگیری می‌توانیم این عبارت را ساده‌تر کنیم. در مرحله بعد، به منظور تعیین اندازه مساحت، مقادیر عددی x و y را درون فرمول بالا قرار می‌دهیم:

$$
=\frac{۵\times ۲^۲ \times ۳} {۱۲}+\frac {۱۵ \times ۲}{۲}-\frac{۲ \times ۳} {۶}-۳
$$

$$
=\frac{۵\times ۱۲} {۱۲}+\frac {۱۵ \times ۲}{۲}-\frac{۶} {۶}-۳
$$

$$
= ۵ + ۱۵ -۱-۳
$$

$$
= ۱۶
$$

در نتیجه، مقدار عددی مساحت متوازی‌الاضلاع برابر 16 سانتی‌متر مربع است.