قطر چیست؟ — قطر در اشکال هندسی

قطر یکی از مفاهیم مهم در شکلهایی نظیر چندضلعیها، چندوجهیها، دایرهها و بیضیها است. در چندضلعیها و چندوجهیها، پارهخط بین گوشهها یا راسهای غیر مجاور، با عنوان قطر شناخته میشود. در دایره و بیضی، به پارهخط گذرنده از مرکز در فاصله بین دو نقطه از محیط، قطر میگویند. قطرها، در محاسبات محیط و مساحت اشکال هندسی مورد استفاده قرار میگیرند. به علاوه، برخی از این پارهخطها، محور تقارن شکلهای هندسی هستند. در این مقاله از مجله فرادرس، به معرفی مفاهیم و فرمولهای مرتبط با قطر انواع شکلهای هندسی میپردازیم و به سوال «قطر در ریاضی چیست ؟» به طور کامل پاسخ میدهیم.
قطر چیست؟
«قطر» (Diagonal)، پارهخطی است که دو راس غیر مجاور در چندضلعیها یا چندوجهیها را به یکدیگر وصل میکند. در دایره، به پارهخطی که از مرکز عبور میکند و دو نقطه انتهایی آن بر روی محیط قرار میگیردن، با عنوان «قطر» (Diameter) شناخته میشود.
تصویر زیر، یک چندوجهی (مکعب) و یک دایره را نمایش میدهد. خطچینهای رسم شده در این اشکال هندسی، بیانگر قطر آنها هستند.

کاربرد قطر چیست ؟
قطر، یکی از اندازههای مهم در بسیاری از شکلهای هندسی است که میتوان از آن برای محاسبه اندازههای دیگر نظیر طول ضلع، محیط، مساحت و غیره استفاده کرد.
قطر در چند ضلعی ها چیست ؟
«چند ضلعی» (Polygon)، یک خط شکسته بسته است که از چندین ضلع، راس و زاویه تشکیل میشود.
تصویر زیر، چند نمونه از چندضلعیها را مشاهده میکنید.
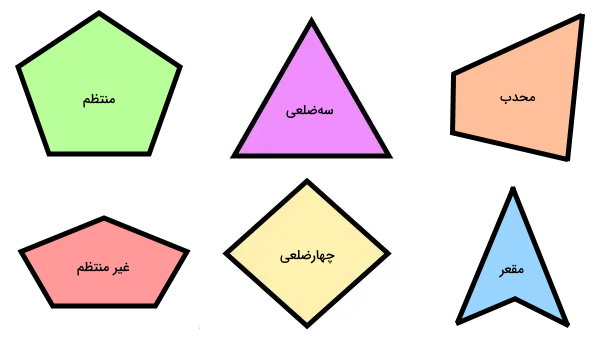
قطر یک چندضلعی، پارهخطی است که دو راس غیر مجاور آن را به یکدیگر وصل میکند. برای درک بهتر این تعریف، چندضلعی زیر را در نظر بگیرید. موقعیت گوشهها یا راسهای این چندضلعی توسط فلش مشخص شده است.
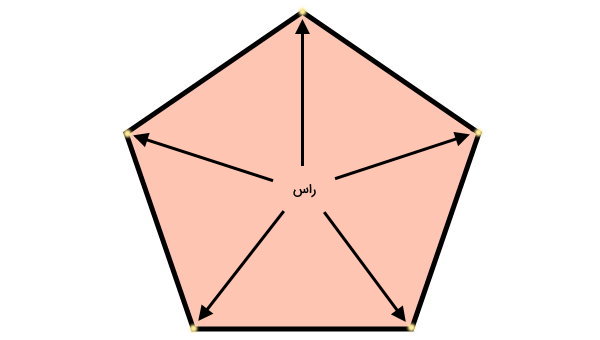
با توجه به تعریف قطر چندضلعی، قلم خود را بر روی یکی از راس قرار میدهیم. سپس، پارهخطی را به سمت یکی از راسهای غیر مجاور رسم میکنیم. این پارهخط، همان قطر چندضلعی است.
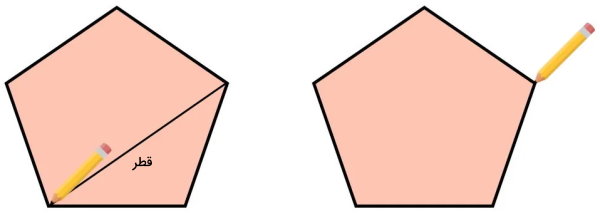
در تعریف و رسم قطرهای چند ضلعی، به غیر مجاور بودن راسها، توجه داشته باشید. این نکته، تفاوت اصلی بین قطر و ضلع است.
تفاوت ضلع و قطر چند ضلعی چیست ؟
ضلع یا لبه چندضلعی، پارهخطی است که دو راس مجاور را به یکدیگر وصل میکند. در صورتی که قطر، پارهخط بین دو راس غیر مجاور است.
تصویر زیر، تفاوت بین قطر و ضلع در یک چندضلعی را نمایش میدهد.

مثال ۱: رسم قطرهای پنج ضلعی
قطرهای پنجضلعی زیر را رسم کنید. این پنجضلعی چند قطر دارد؟
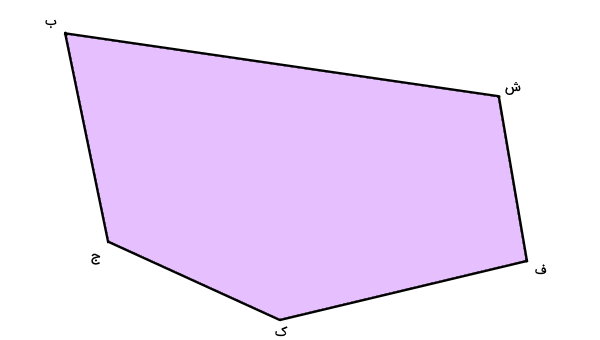
تصویر بالا، پنجضلعی «ب ج ک ف ش» را نمایش میدهد. به منظور رسم قطرهای این پنجضلعی، یکی از راسهای آن مانند راس «ش» را در نظر میگیریم. قلم خود را بر روی این راس قرار میدهیم.
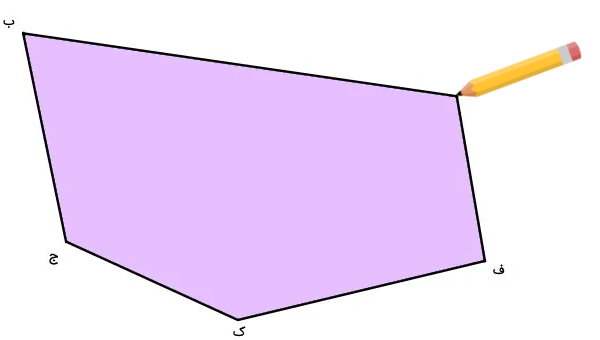
راسهای «ج» و «ک»، راسهای غیر مجاور با راس «ش» هستند. پارهخطی را از راس «ش»، پارهخطی را تا یکی از راسهای غیر مجاور رسم میکنیم.
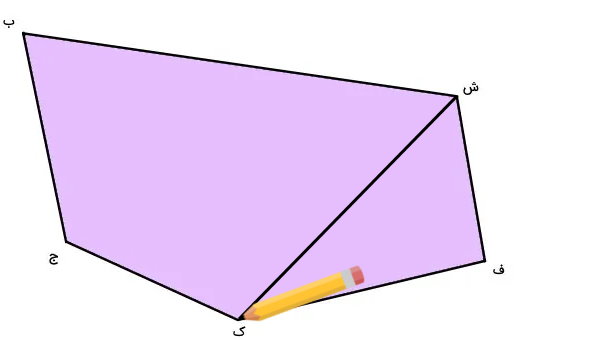
این کار را برای راس غیر مجاور بعدی نیز انجام میدهیم.
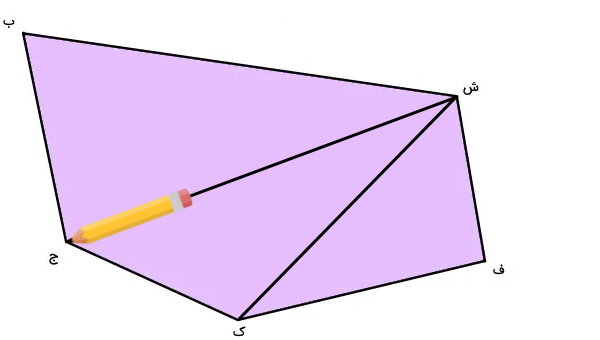
دیگر هیچ راس غیر مجاوری با راس «ش» وجود ندارد. بنابراین، به سراغ راسهای دیگر میرویم. مراحل بالا را برای این راسها نیز تکرار میکنیم. به این ترتیب، تمام قطرهای پنجضلعی رسم میشوند.
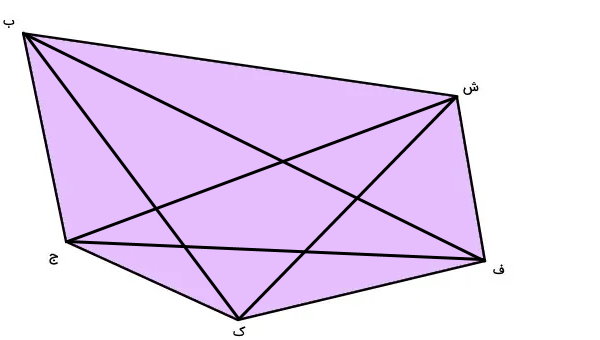
تصویر زیر، تمام قطرهای رسم شده پنجضلعی را نمایش میدهد. تعداد این قطرها برابر با ۵ است. البته، میتوانستیم تعداد قطرهای پنجضلعی را توسط یک فرمول مخصوص نیز به دست بیاوریم. در بخش بعدی به معرفی این فرمول میپردازیم.
فرمول تعداد قطر چند ضلعی چیست ؟
تعداد قطرهای چندضلعی از رابطه زیر به دست میآید:
۲ ÷ [(۳ - تعداد ضلعها) × تعداد ضلعها] = تعداد قطرها
عبارت جبری فرمول تعداد قطرهای چندضلعی به صورت زیر نوشته میشود:
در این فرمول داریم:
- dn: تعداد قطرهای چندضلعی
- n: تعداد ضلعهای چندضلعی
بر اساس فرمول بالا، تعداد قطرهای یک چندضلعی، فقط به تعداد ضلعهای آن بستگی دارد.
مثال ۱: محاسبه تعداد قطرهای هشت ضلعی
اندازه تمام ضلعهای یک هشتضلعی برابر با ۱۰ سانتیمتر است. تعداد قطرهای این هشتضلعی را به دست بیاورید.
تعداد قطرهای یک چندضلعی، با توجه به تعداد ضلعهای آن تعیین میشود و به اندازههای دیگری نظیر ضلع ارتباط ندارد. بر اساس فرمول تعداد قطرهای چندضلعی، داریم:
در این فرمول داریم:
- dn: تعداد قطرهای هشتضلعی
- n: تعداد ضلعهای هشتضلعی برابر با ۸
تعداد ضلعها درون فرمول قرار میدهیم و آن را حل میکنیم:
در نتیجه، یک هشتضلعی، ۲۰ قطر دارد.
قطر سه ضلعی یا قطر مثلث چیست ؟
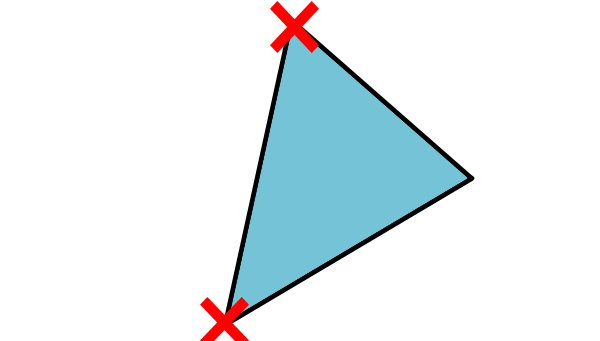
مثلث، شکلی متشکل از سه ضلع و سه راس است. در این شکل، تمام راسها، در مجاورت یکدیگر قرار دارند. به عبارت دیگر، هیچ یک از دو راس مثلث، غیر مجاور نیستند. بنابراین، مثلث، هیچ قطری ندارد.
قطر چهار ضلعی چیست ؟
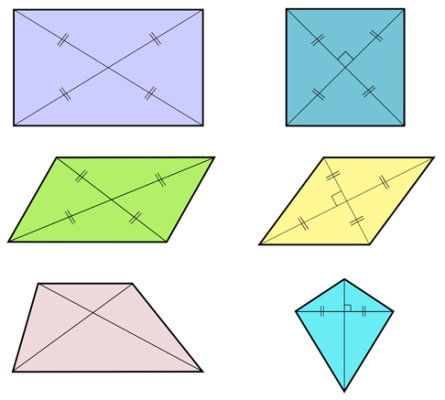
چهارضلعی، شکلی متشکل از چهار ضلع و چهار راس است. از شناخته شدهترین چهارضلعیها میتوان به مربع، مستطیل، لوزی، متوازیالاضلاع و ذوزنقه اشاره کرد. تمام چهارضلعیها، دو قطر دارند. تصویر زیر، قطرهای این اشکال هندسی را نمایش میدهد.
قطر مربع چیست ؟
مربع، یکی از انواع چهارضلعیها است که از چهار ضلع با اندازههای برابر و چهار زاویه ۹۰ درجه تشکیل میشود. این شکل هندسی نیز مانند تمام چهارضلعیها، ۲ قطر دارد. قطرهای مربع هماندازه هستند و وسط یکدیگر را با زاویه ۹۰ قطع میکنند. به عبارت دیگر، قطرهای مربع، عمود منصف یکدیگرند. دو محور تقارن از چهار محور تقارن مربع، قطرهای این شکل هستند.

در مربع، قطرها، زوایای داخلی را به دو زاویه ۴۵ درجه تقسیم میکنند. در واقع، قطرهای مربع، نیمساز زوایای داخلی آن هستند. با رسم یکی از قطرها، مربع به دو مثلث قائم الزاویه و با رسم هر دو قطر (مانند تصویر بالا)، مربع به چهار مثلث قائم الزاویه تقسیم میشود.
رابطه بین ضلع و قطر مربع چیست ؟
بر اساس قضیه فیثاغورس، رابطه بین ضلع و قطر مربع عبارت است از:
در این رابطه داریم:
- d: قطر مربع
- a: ضلع مربع
محاسبه محیط مربع با قطر چگونه است ؟
محیط مربع، از رابطه «اندازه یک ضلع ضربدر ۴» محاسبه میشود. به دلیل رابطه بین ضلع و قطر، فرمول محیط مربع با قطر عبارت است از:
در این فرمول داریم:
- P: محیط
- d: قطر
محاسبه مساحت مربع با قطر چگونه است ؟
مساحت مربع، از «اندازه یک ضلع ضربدر خودش» به دست میآید. فرمول مساحت مربع را میتوان بر حسب قطر نیز نوشت:
- A: مساحت مربع
- d: قطر مربع
برای آشنایی بیشتر با فرمول بالا، مطالعه مطلب «مساحت مربع با قطر چگونه بدست می آید؟ – به زبان ساده + حل تمرین و مثال» را به شما پیشنهاد میکنیم.
قطر مستطیل چیست ؟
در مستطیل، چهار زاویه قائمه دارد. به علاوه، در این شکل، ضلعهای روبهرویی با یکدیگر موازی و مساوی هستند. مستطیل، ۲ قطر هماندازه دارد. اغلب ویژگیهای قطر مستطیل، مشابه با قطر مربع است. با این تفاوت که قطرهای مستطیل، یکدیگر را با زاویه ۹۰ درجه قطع نمیکنند. در واقع، به مستطیلی که قطرهای عمود برهم داشته باشد، مربع میگویند.
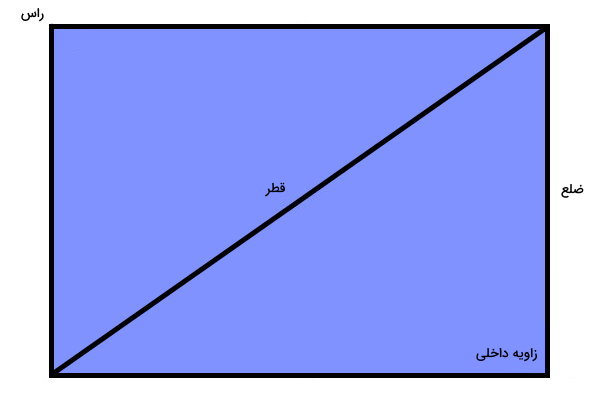
رابطه بین طول و عرض با قطر مستطیل چیست ؟
رابطه بین قطر مستطیل با طول و عرض آن به صورت زیر نوشته میشود:
در این رابطه داریم:
- d: قطر مستطیل
- w: عرض مستطیل
- l: طول مستطیل
محاسبه محیط مستطیل با قطر چگونه است ؟
محیط مستطیل، از مجموع طول و عرض آن به دست میآید. با توجه به رابطه بین قطر با طول و عرض میتوانیم فرمول محیط مستطیل را بر حسب قطر بنویسیم:
در این فرمول داریم:
- P: محیط مستطیل
- a: یکی از ضلعهای مستطیل (طول یا عرض)
- d: قطر مستطیل
محاسبه مساحت مستطیل با قطر چگونه است ؟
مساحت مستطیل، «حاصلضرب طول در عرض» است. فرمول مساحت مستطیل بر حسب قطر به صورت زیر نوشته میشود:
در این فرمول داریم:
- A: مساحت
- a: یکی از ضلعها
- d: قطر
قطر لوزی چیست ؟
لوزی، دارای چهار ضلع با اندازه برابر است که دو راس با زاویه حاده و دو راس با زاویه منفرجه دارد. لوزی، ۲ قطر با ویژگیهای مشابه با قطرهای مربع دارد. با این تفاوت که در لوزی، اندازه قطرها برابر نیست. به همین دلیل، قطرهای لوزی با عنوان «قطر بزرگ» و «قطر کوچک» شناخته میشوند.
این قطرها، معمولا در محاسبه مساحت لوزی مورد استفاده قرار میگیرند.
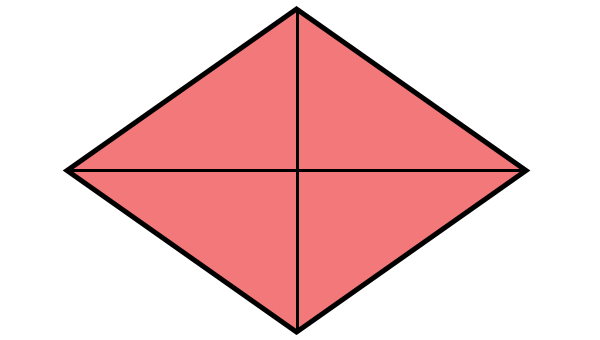
رابطه بین ضلع و قطرهای لوزی چیست ؟
اندازه هر یک از ضلعهای لوزی را میتوان با استفاده از اندازه قطرهای بزرگ و کوچک آن به دست آورید:
در این فرمول داریم:
- a: اندازه ضلع لوزی
- q: اندازه یکی از قطرها
- p: اندازه قطر دیگر
محاسبه محیط لوزی با قطر چگونه است ؟
محیط لوزی، چهار برابر اندازه ضلع آن است. فرمول محیط لوزی با قطر، به صورت زیر نوشته میشود:
در این فرمول داریم:
- P: محیط لوزی
- q: اندازه یکی از قطرها
- p: اندازه قطر دیگر
محاسبه مساحت لوزی با قطر چگونه است ؟
مساحت لوزی، از «حاصلضرب قطرها تقسیم بر ۲» به دست میآید. عبارت جبری فرمول مساحت لوزی با قطر عبارت است از:
در این فرمول داریم:
- A: مساحت لوزی
- p: اندازه یکی از قطرها
- q: اندازه قطر دیگر
به این ترتیب، فرمول محاسبه قطر لوزی به صورت زیر نوشته میشود:
در صورت تمایل به یادگیری بیشتر راجع به مساحت لوزی با قطر و بدون قطر، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
- مساحت لوزی با قطر چگونه بدست میآید؟ — به زبان ساده + حل تمرین و مثال
- مساحت لوزی بدون قطر چگونه بدست میآید؟ — به زبان ساده + حل مثال
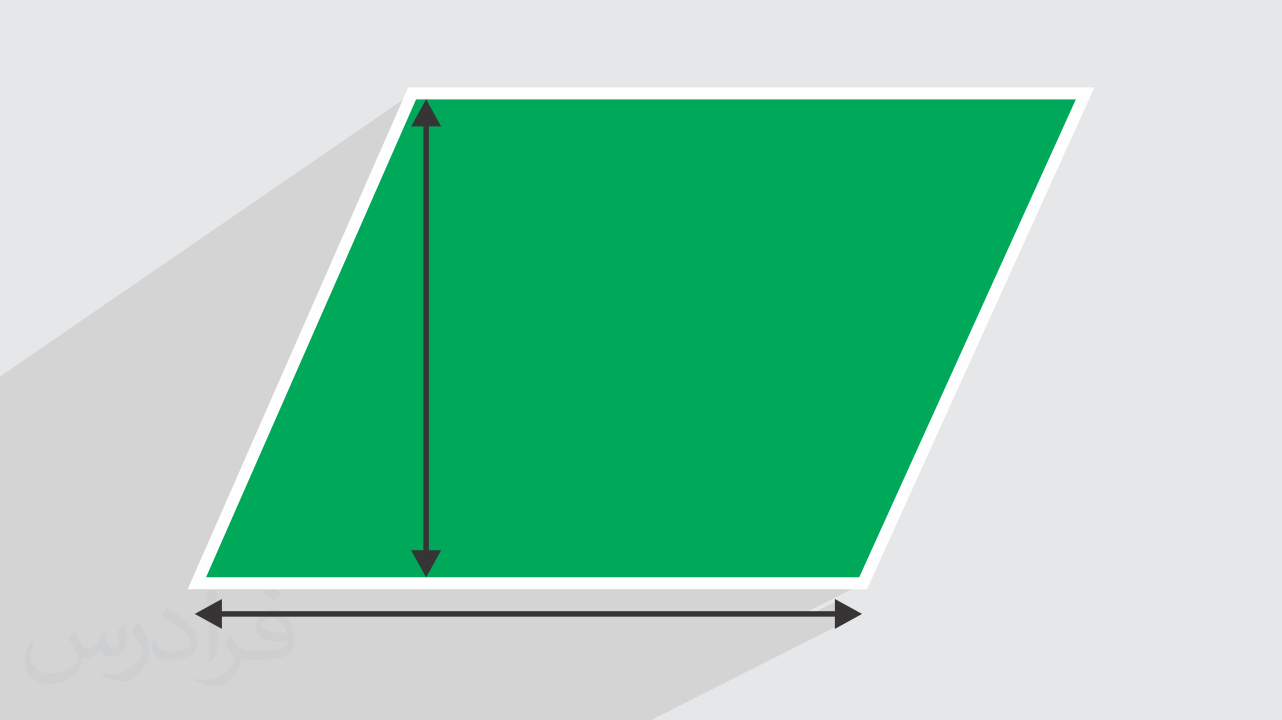
قطر متوازی الاضلاع چیست ؟
متوازیالاضلاع، شکلی با ضلعهای روبهرویی مساوی و موازی است. مربع، مستطیل و لوزی، از انواع خاص متوازیالاضلاع در نظر گرفته میشوند. این شکل، دو قطر دارد.
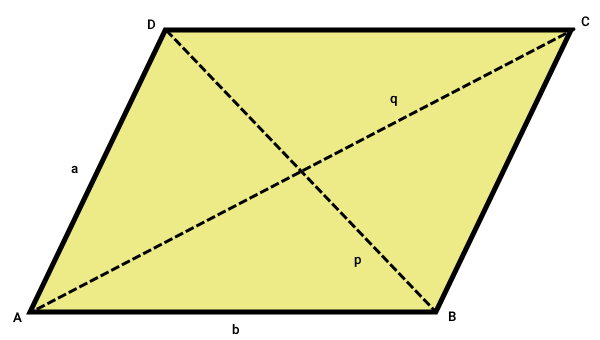
اندازه قطرهای متوازیالاضلاع، از فرمولهای زیر به دست میآید:
در این فرمولها داریم:
- p: یکی از قطرهای متوازیالاضلاع
- q: قطر دیگر متوازیالاضلاع
- a: یکی از ضلعهای متوازیالاضلاع
- b: ضلع دیگر متوازیالاضلاع
محاسبه مساحت متوازی الاضلاع با قطر چگونه است ؟
فرمول مساحت متوازی الاضلاع با قطر عبارت است از:
در فرمول بالا داریم:
- A: مساحت متوازیالاضلاع
- p: اندازه یکی از قطرها
- q: اندازه قطر دیگر
- α: زاویه برخورد دو قطر (یکی از دو زاویه برخورد)
امکن محاسبه محیط متوازیالاضلاع با استفاده از اندازه قطر آن نیز وجود دارد. در صورت تمایل به یادگیری در مورد این موضوع و مساحت متوازیالاضلاع، مطالعه مطالب زیر از مجله فرادرس را به شما پیشنهاد میکنیم:
- محیط متوازیالاضلاع چیست؟ — به زبان ساده + حل تمرین و مثال
- مساحت متوازیالاضلاع چیست؟ — فیلم آموزش رایگان + حل تمرین و مثال
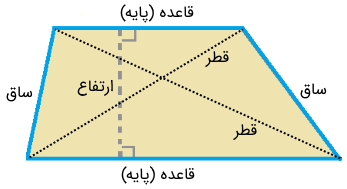
قطر ذوزنقه چیست ؟
ذوزنقه، شکلی با دو ضلع موازی و دو ضلع غیر موازی است. از انواع ذوزنقه میتوان به ذوزنقه قائمالزاویه، ذوزنقه متساویالساقین و ذوزنقه مختلفالاضلاع اشاره کرد. هر ذوزنقه، ۲ قطر دارد. قطرهای ذوزنقه متساویالساقین (ذوزنقهای با دو ساق برابر)، هماندازه هستند.
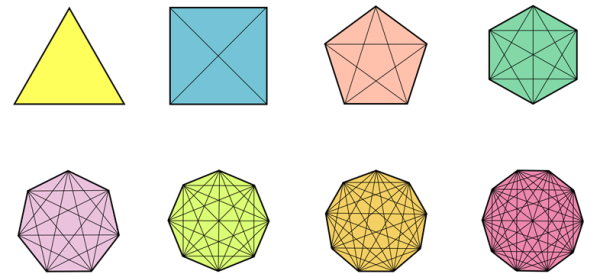
قطر چند ضلعی منتظم چیست ؟
چندضلعی منتظم، دارای ضلعها و زاویههای برابر است. مربع، یک چهارضلعی منتظم است. شکلهای منتظم، قطرهای هماندازه دارند. در زوجضلعیهای منتظم (مربع، ششضلعی، هشتضلعی و غیره)، قطرها محورهای تقارن شکل نیز هستند.
قطر چند ضلعی نامنتظم چیست ؟
به چندضلعیهایی که تمام ضلعها و زاویههای آنها با هم برابر نباشند، چندضلعی نامنتظم یا نامنظم میگویند. در بخشهای قبلی، قطرهای برخی از چندضلعیهای نامنتظم مانند مستطیل، لوزی، متوازیالاضلاع و ذوزنقه را معرفی کردیم. قطرهای چندضلعیهای منتظم و نامنتظم، تفاوتی از نظر تعداد با یکدیگر ندارند. برای تایید این موضوع میتوانید تصویر زیر را با تصویر قطرهای چندضلعیهای منتظم مقایسه کنید.

جدول زیر، تعداد قطرهای چندضلعیهای مختلف را بر اساس تعداد ضلع نمایش میدهد.
| چندضلعی | تعداد قطرها |
| سه ضلعی | ۰ |
| چهار ضلعی | ۲ |
| پنج ضلعی | ۵ |
| شش ضلعی | ۹ |
| هفت ضلعی | ۱۴ |
| هشت ضلعی | ۲۰ |
| نه ضلعی | ۲۷ |
| ده ضلعی | ۳۵ |
قطر چند ضلعی محدب و مقعر چیست ؟
چندضلعی محدب، از زاویههای کوچکتر از ۱۸۰ درجه تشکیل میشود. تمام شکلهایی که تا به اینجای مقاله معرفی کردیم، شکلهای محدب بودند. در چندضلعیهای محدب، قطرها درون محیط شکل قرار میگیرند. بررسی این ویژگی، یکی از روشهای تشخیص چندضلعیهای محدب است.
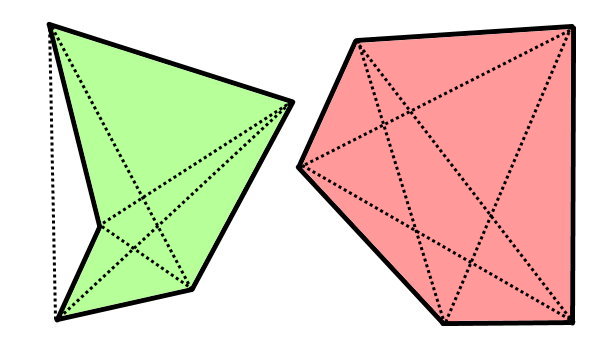
چندضلعی مقعر، حداقل یک زاویه بزرگتر از ۱۸۰ درجه دارد. به همین دلیل، حداقل یکی از قطرهای این شکل در خارج از محیط آن قرار میگیرد. تعداد قطرهای n ضلعیهای محدب و مقعر نیز از رابطه ۲ ÷ [(۳ - n) × n] به دست میآید.
قطر در دایره چیست ؟
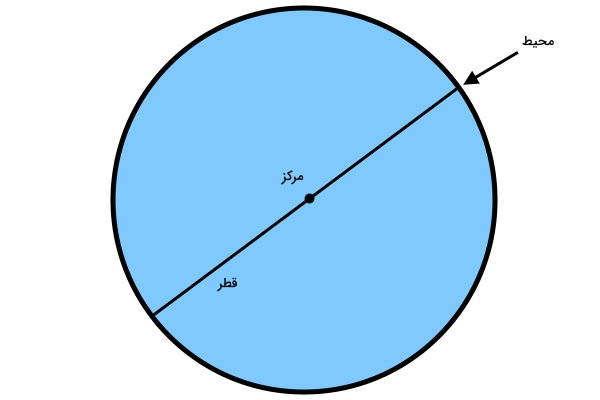
قطر دایره، پارهخطی است که از مرکز دایره عبور کرده و دو نقطه بر روی محیط آن را به یکدیگر وصل میکند. قطر، یکی از مهمترین اندازههای دایره محسوب میشود.
محیط دایره از بینهایت نقطه تشکیل میشود. از روی هر یک از این نقاط میتواند یک قطر رسم کرد. بنابراین، دایره بینهایت قطر دارد. 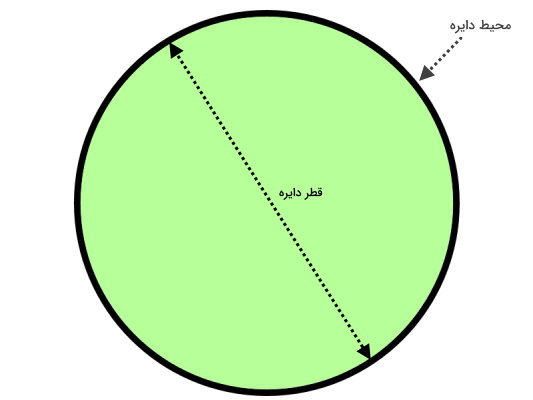
قطر دایره، بزرگترین وتر آن نیز محسوب میشود. این اندازه در محاسبه محیط و مساحت دایره مورد استفاده قرار میگیرد.
محاسبه محیط دایره با قطر چگونه است ؟
محیط دایره، اندازه دور این شکل هندسی است. نسبت محیط دایره به قطر آن، همواره برابر با ۳/۱۴ میشود. به این عدد ثابت، عدد پی میگویند. بر این اساس، محیط دایره با استفاده از فرمول زیر به دست میآید:
قطر × ۳/۱۴ = محیط دایره
عبارت جبری فرمول محیط دایره با قطر نیز به صورت زیر نوشته میشود:
- C: محیط دایره
- π: عدد ثابت ۳/۱۴
- d: قطر دایره
محاسبه مساحت دایره با قطر چگونه است ؟
مساحت دایره، اندازه سطح درون آن است که از فرمول زیر به دست میآید:
شعاع × شعاع × عدد پی = مساحت دایره
شعاع دایره، نصف قطر آن است. بنابراین میتوانیم فرمول بالا را به صورت زیر بازنویسی کنیم:
[۴ ÷ (قطر × قطر)] × عدد پی = مساحت دایره
عبارت جبری فرمول مساحت دایره با قطر به صورت زیر نوشته میشود:
- A: مساحت دایره
- π: عدد ثابت ۳/۱۴
- d: قطر دایره
فرق بین قطر و شعاع دایره چیست ؟
شعاع دایره، پارهخطی است که مرکز این شکل را به یک نقطه بر روی محیط آن وصل میکند.
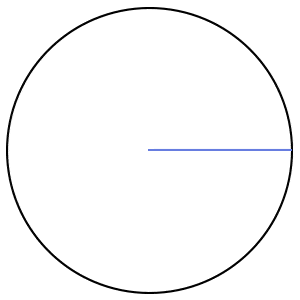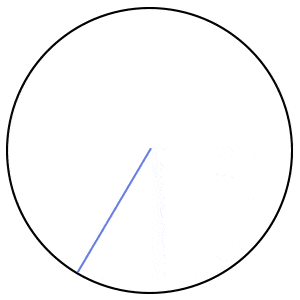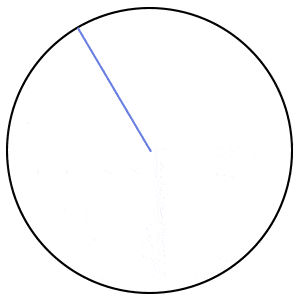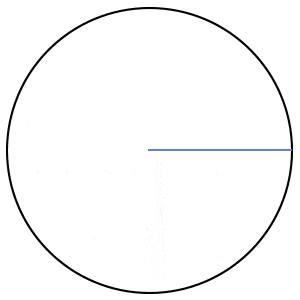
قطر دایره، دو برابر شعاع آن است. در واقع هر قطر، از دو شعاع تشکیل میشود.
قطر نیم دایره چیست ؟
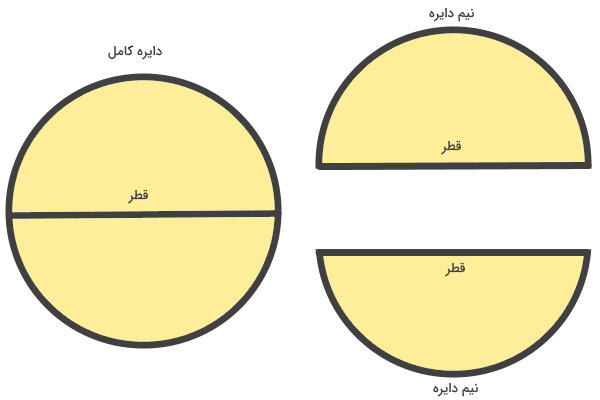
اگر یک دایره را از روی یکی از قطرهایش به دو قسمت مساوی تقسیم کنیم، به هر قسمت، یک نیمدایره میگویند. نیمدایره، از یک کمان و یک پارهخط تشکیل میشود. پارهخط بین دو انتهای کمان، همان قطر نیمدایره است.
محیط و مساحت نیم دایره
محیط و مساحت نیمدایره، با استفاده از محیط و مساحت دایره محاسبه میشود. فرمول محیط نیمدایره عبارت است از:
قطر دایره + نصف محیط دایره = محیط نیم دایره
مساحت نیمدایره، از نصف مساحت دایره به دست میآید:
۲ ÷ مساحت دایره = مساحت نیمدایره
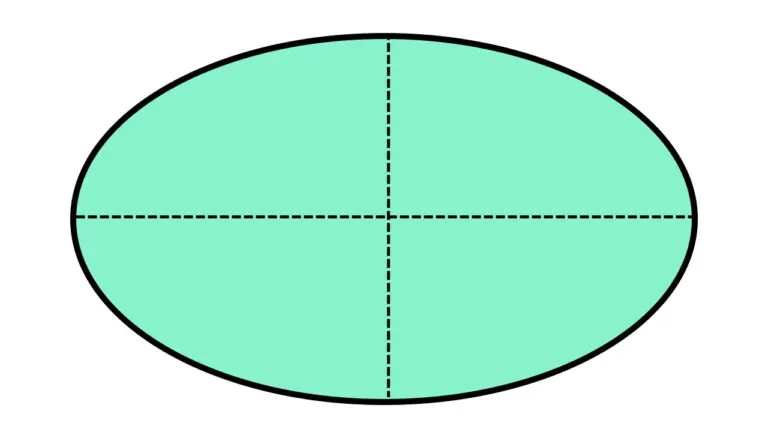
قطر بیضی چیست ؟
به پارهخطی که دو نقطه روبهرویی بر روی محیط بیضی را به هم وصل میکند، قطر بیضی میگویند. برخلاف دایره، قطرهای بیضی، هماندازه نیستند. بیضی دو قطر با بیشترین و کمترین اندازه دارد. به قطر بزرگ بیضی، محور اصلی و به قطر کوچک آن، محور فرعی میگویند. کانونهای بیضی، بر روی قطر بزرگ آن قرار دارند. قطرهای بیضی، محیط آن را در نقاطی با عنوان گوشه قطع میکنند.
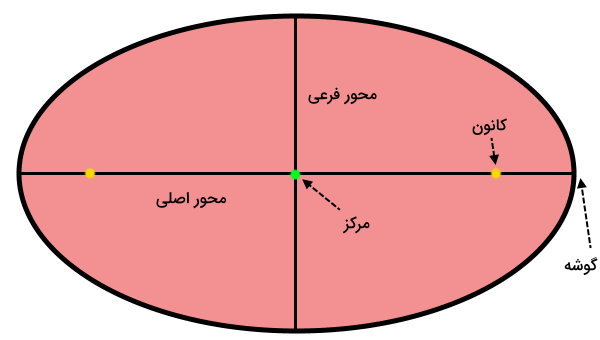
به فاصله مرکز تا گوشهها، شعاع بیضی میگویند. اندازه شعاع کوچک بیضی، نصف قطر کوچک و اندازه شعاع بزرگ بیضی، نصف قطر بزرگ آن است. شعاعها، به منظور تعیین محیط و مساحت بیضی مورد استفاده قرار میگیرند. بنابراین، قطر، به صورت غیر مستقیم در محاسبات بیضی تاثیر میگذارد.
قطر در چند وجهی ها چیست ؟
تعریف قطر در چندوجهیها، مشابه تعریف قطر در چندضلعیها است. به پارهخطی که بین دو راس غیر مجاور چندوجهی رسم شود، قطر آن چندوجهی میگویند. چندوجهیها، دو نوع قطر دارند. انواع قطرهای چندوجهی را بر روی یک مکعب توضیح میدهیم.
مکعب، یک چندوجهی است که از شش وجه مربعی شکل تشکیل میشود. هر یک از وجههای این شکل، دو قطر دارند. این قطرها را میتوان به عنوان قطرهای جانبی مکعب در نظر گرفت. علاوه بر این، از اتصال هر راس به دیگر راسهای غیر مجاور بر روی وجههای دیگر، قطرهای داخلی مکعب تشکیل میشوند.
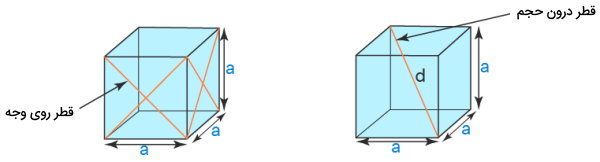
اندازه قطرهای روی وجههای مکعب، از همان فرمول اندازه قطر دایره به دست میآید:
در این رابطه داریم:
- dF: قطر روی وجه مکعب
- a: اندازه ضلع مکعب
اندازه قطرهای درون حجم مکعب نیز با استفاده از فرمول زیر محاسبه میشود:
- dB: قطر درون حجم مکعب
- a: اندازه ضلع مکعب
اثبات اندازه قطر مکعب بر اساس قضیه فیثاغورس انجام میگیرد.
تفاوت خط تقارن و قطر چیست ؟
خط تقارن یا «محور تقارن» (Axis of Symmetry)، خطی است که شکل را به دو قسمت مساوی تقسیم میکند. به این ترتیب، به ازای هر نقطه در یک سمت خط تقارن، نقطهای متناظر در سمت دیگر وجود دارد. اگر یک شکل را از روی محور تقارنش تا بزنیم، هر دو سمت به طور کامل بر روی یکدیگر قرار میگیرند. تصویر زیر، مفهوم محور تقارن در یک مستطیل را نمایش میدهد.
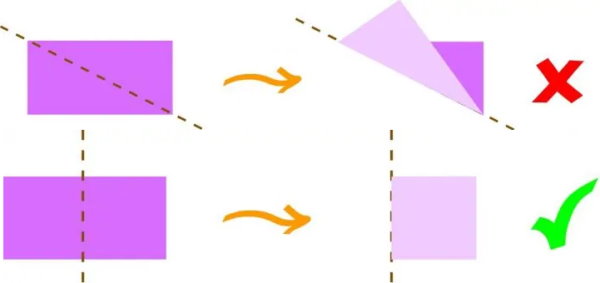
در مستطیل بالایی، شکل از روی قطر تا خورده است و دو طرف تاخوردگی بر روی یکدیگر منطبق نشدهاند. بنابراین، قطر مستطیل، نمیتواند خط تقارن آن باشد. در مستطیل پایینی، مستطیل از روی خط تقارن تا خورده است. به همین دلیل، هر دو طرف تاخوردگی بر روی هم منطبق شدهاند. در چندضلعیهای منتظم، قطر میتواند خط تقارن نیز باشد. تصویر زیر، خط تقارن چند ضلعیهای منتظم را نمایش میدهد.
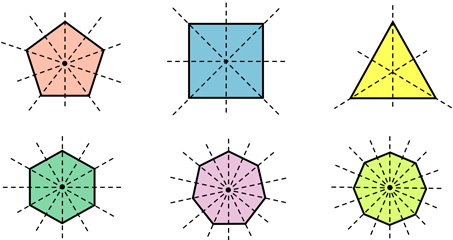
همانطور که مشاهده میکنید، در زوجضلعیهای منتظم (مربع، ششضلعی منتظم، هشتضلعی منتظم و غیره)، قطرها، محور تقارن شکل هستند. در واقع، در این چندضلعیهای منتظم، قطرها، نیمی از محورهای تقارن را تشکیل میدهند. در فردضلعیهای منتظم (مثلث، پنجضلعی منتظم، هفتضلعی منتظم و غیره)، میانه ضلعها، خط تقارن شکل هستند.
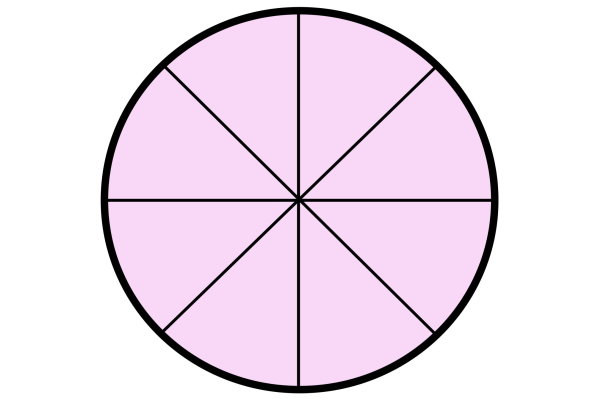
به غیر از چندضلعیهای منتظم، قطر شکلهای دیگری نظیر لوزی، شبهلوزی، دایره، بیضی و غیره نیز میتواند این شکلها را به دو قسمت مساوی تقسیم کند. در دایره، قطر، همان خط تقارن است. بنابراین، دایره، بینهایت خط تقارن دارد. در بیضی، دو قطر بزرگ و کوچک به عنوان خط تقارن شکل محسوب میشوند.
سوالات متداول در رابطه با قطر در اشکال هندسی
در این بخش، به برخی از سوالات پرتکرار در رابطه با قطر شکلهای هندسی به طور مختصر پاسخ میدهیم.
تعریف قطر چند ضلعی چیست ؟
قطر یک چندضلعی، پارهخط اتصالدهنده گوشههای غیر مجاور آن است.
قطر مربع چند برابر ضلع مربع است ؟
قطر مربع، رادیکال 2 برابر ضلع آن است.
کدام چند ضلعی قطر ندارد ؟
مثلث یا سهضلعی، هیچ قطری ندارد.
قطر کره زمین چقدر است؟
کره زمین، یک شکل بیضوی با قطر 12742 کیلومتر است.
چند ضلعی ها چند قطر دارند ؟
هر n ضلعی، ۲ ÷ [(۳ - n) × n] قطر دارد.
قطرهای کدام شکل با هم برابر هستند ؟
قطرهای چندضلعیهای منتظم با هم برابر هستند. البته دایره نیز قطرهای هماندازه دارد.
آیا قطرهای لوزی با هم برابرند؟
خیر. قطرهای لوزی بر هم عمودند. فقط قطرهای یک نوع لوزی (مربع)، با هم برابرند.
فرق قطر و خط تقارن چیست ؟
قطر، دو گوشه غیر مجاور را به هم وصل میکند؛ در صورتی که خط تقارن، شکل را به دو قسمت مساوی تقسیم میکند.
آیا قطر خط تقارن است ؟
قطر لزوما خط تقارن شکل نیست. با این وجود، قطرهای برخی از شکلها (مانند لوزی) میتوانند آنها را به دو قسمت مساوی تقسیم کنند.
مثلث چند قطر دارد ؟
مثلث، قطر ندارد.
مربع چند قطر دارد ؟
مربع، 2 قطر دارد.
مستطیل چند قطر دارد ؟
مستطیل، 2 قطر دارد.
ذوزنقه چند قطر دارد ؟
ذوزنقه، 2 قطر دارد.
پنج ضلعی چند قطر دارد ؟
5 ضلعی، 5 قطر دارد.
شش ضلعی چند قطر دارد ؟
6 ضلعی، 9 قطر دارد.
تعریف قطر دایره چیست ؟
قطر یک دایره، پارهخط گذرنده از مرکز آن است که دو نقطه از محیط را به یکدیگر متصل میکند.
دایره چند قطر دارد ؟
دایره، بینهایت قطر دارد.
بیضی چند قطر دارد؟
بیضی، دو قطر (یک محور اصلی و یک محور فرعی) دارد.
قطر دایره چند برابر شعاع دایره است ؟
قطر دایره، دو برابر شعاع آن است.
فرق بین وتر و قطر دایره چیست ؟
به هر پارهخطی که دو نقطه از محیط دایره را به هم وصل کند، وتر میگویند. قطر، بزرگترین وتر دایره است.
نسبت محیط به قطر دایره چیست؟
نسبت محیط به قطر دایره، عدد ثابت ۳/۱۴ یا همان عدد پی است.
آیا قطر دایره خط تقارن آن است ؟
بله. قطر دایره، آن را به دو قسمت مساوی تقسیم میکند.












با سلام . لطفا متن پاراگراف اول را اصلاح بفرمایید… ممنون از شما
«قطر» (Diagonal)، پارهخطی است که دو راس غیر مجاور در چندضلعیها یا چندوجهیها را به یکدیگر ……..وسط ……….میکند
………وصل می کند…………
با سلام و وقت بخیر؛
متن مقاله اصلاح شد.
از همراهیتان با مجله فرادرس سپاسگزاریم.
خوب بود
دایره بی نهایت قطر داره؟
باعرض سلام و وقت بخیر .قطر را به عنوان خط بیان کردید ولی بهتر هست که برای جلوگیری از بدفهمی قطر رو پاره خطی که دو راس غیر مجاور را به یکدیگر وصل می کند بیان کنیم. خسته نباشید
سلام.
متن اصلاح شد.
از همراهی و بازخورد شما سپاسگزاریم.
خوبه یعنی بی عالیه ممنون از سازندش
بده من که نفهمیدم??
عالی بود. خیلی خوب توضیح داد. و ممنون از آموزش فرمول. چون تا حالا نشنیده بودم و الان که اینو دیدم خیلی به دردم خورد چون من شیشم هستم و تقریبا ده روز روز دیگه تیزهوشان دارم و این خیلی به دردم خورد.
آقا میشه بگید که چجوری میتوانیم کسری را به عدد اعشاری تبدیل کنیم ؟
سلام. اول مخرج کسر رو به 10، 1000،100و…
تبدیل می کنیم. یعنی باضرب کردن. و یادت باشه صورت هم ضرب کنی. بعد که انجام دادی این کار رو کن. به عنوان مثال میخوای یک پنجم رو به اعشار تبدیل کنی،
یک پنجم رو در 2 ضرب می کنی،که پاسخش میشه دو دهم. بعد فقط به اعشار مینویسی:0/2
باید صورتو در مخرج ضرب کنی
امممممم سلام
من چیز زیادی از ایکس و از این جور چیز ها نفهمیدم
فکر نکنید خنگقم ها ?
بلکه من ۱۳ سال دارم و کلاس ششم دبستانم ???
ولی چیزی که من از قطر فهمیدم این است که وقتی دو راس را به هم وصل کنیم قطر است ?
ولی ممنونم ?
البته چون من اینترنتم ضعیف است فیلم را متاسفانه نگاه نکردم ???
ولی باز هم ممنون ?
خیلی مفید بود ?
خدانگهدار ?
خوبه?
فقط آموزش ویدیویی خیلی عالی
آقا میشه بگین با این فرمول ۵۴=۲/(۳-۱۲)۱۲ ما چطور میتونیم x(x-3)/2=54 میزان ایکس رو به دست بباریم؟
ببین اگه که ما داخل یه ضرب دو طرف رو جمع منها ضرب یا تقسیم بر یه عبارت کنیم باید علامت مساوی برقرار باشه یعنی مثلا اگه داشته باشیم۶=۳×۲ حالا اگه دو طرف مساوی رو مثلا در۵ ضرب کنیم میشه۶×۵=۳×۲×۵ که میشه ۳۰=۳۰که بازم ۳۰ برابر ۳۰ هست یا مثلا اگه همینو منهای ۴ کنیم میشه ۴-۶=۴-۳×۲ که با توجه به اینکه ضرب بر جمع مقدمه اول ضرب می کنیم بعد کم می کنیم که میشه ۲=۲پس بازم برابر شد .
حالا اگه در عبارت ۵۴=۲/(۳-x(x ما بیایم تقسیم بر دو رو از بین ببریم یعنی اگه ما هر دو طرف رو ضرب در ۲ کنیم بازم مساوی هم میشه و کسر از بین می ره که میشه ۱۰۸=(۳-x(x .حالا اگه گفتین چه عددی ضرب در ۳تا کمترش بشه که جواب بشه ۱۰۸؟ میشه ۱۲ پس اون شکل ما ۱۲ ضلعی بوده.که در واقع ۱۲ ضرب در ۹ کنیم میشه ۱۰۸ و تقسیم بر ۲ میشه ۵۴.پس درست به دست آوردیم.موفق باشید
کم اطلاعات داشت و برای کلاس سوم مناسب نبود
من راضی نبودم
سلام. صبحتون بخير. خوبيد؟؟
ممنون از مطالب و سايت خوبتون.
عالیهههههههههههههه
عالیهههههههههههههههههه
عالیههههههههههههههههههههه
خیلی خوب بود