مساحت چیست؟ — به زبان ساده + حل مثال های متنوع

مساحت، اندازه درون شکلهای دوبعدی و سطح بیرونی شکلهای سهبعدی است. فرمولهای متعددی برای محاسبه مساحت شکلهای مختلف هندسی وجود دارند. به عنوان مثال، مساحت مثلث از «حاصلضرب قاعده در ارتفاع تقسیم بر ۲»، مساحت مربع از «حاصلضرب یک ضلع در خودش»، مساحت مستطیل از «حاصلضرب طول در عرض» و مساحت دایره از «حاصلضرب عدد پی در مربع شعاع» به دست میآید. در این مقاله از مجله فرادرس، قصد داریم به سوالهایی نظیر «مساحت چیست؟»، «مساحت شکلهای هندسی چگونه به دست میآید؟» و «تفاوت مساحت با محیط و حجم چیست؟» پاسخ دهیم.
مساحت چیست ؟
«مساحت» (Area)، اندازه سطحی است که توسط یک شکل پوشش داده میشود. به عبارت دیگر، مساحت، اندازه سطح درون یک شکل است.
تصویر زیر را در نظر بگیرد. این تصویر، یک منحنی بسته را نمایش میدهد. به اندازه این منحنی، محیط میگویند.
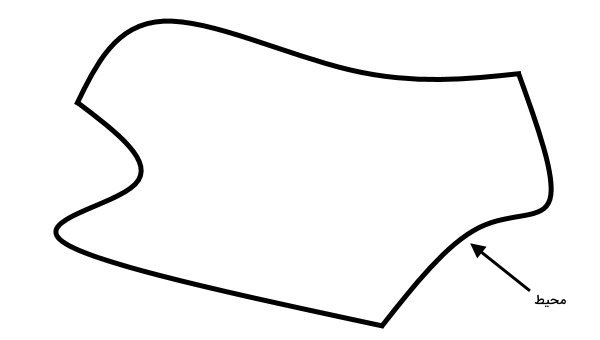
فضای درون محیط را رنگ میکنیم. ناحیه رنگی، مساحت شکل را نمایش میدهد. اندازهگیری این ناحیه به ما کمک میکند تا میزان سطح پوشش داده شده توسط شکل را تعیین کنیم.
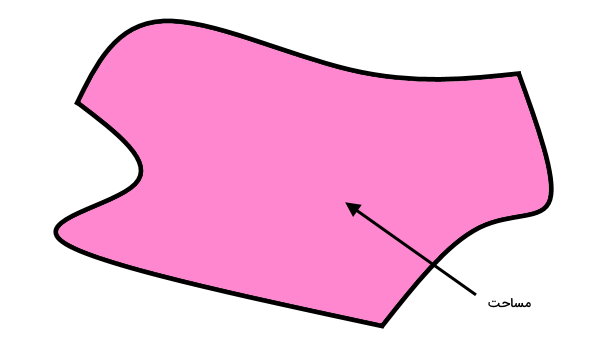
مساحت چه کاربردی دارد ؟
مساحت، یکی از پرکاربردترین و مهمترین مفاهیم ریاضی در زندگی ما است. در گذشته، از این مفهوم برای تعیین اندازه زمینهای کشاورزی استفاده میشد. مفهوم مساحت، در بسیاری از سازههای باستانی نظیر اهرام ثلاثه مصر نیز به کار گرفته شده است. با گذشت زمان، فرمولهای مختلفی برای محاسبه مساحت مساحت شکلهای مختلف ارائه شد. امروزه، این فرمولها در بسیاری از فعالیتهای ساده مانند تعیین مساحت کف یک اتاق تا فعالیتهای تخصصی نظیر محاسبه مساحت قطعات مکانیکی به کار میرود.

به عنوان مثال، فرض کنید میخواهیم یک فرش مناسب برای اتاق خود انتخاب کنیم. اگر مساحت فرش انتخابی بزرگتر از اندازه کف اتاق باشد، استفاده از آن مناسب نخواهد بود. در صورت کوچک بودن فرش به اندازه زیاد نیز، کف اتاق به خوبی پوشیده نمیشود. به این ترتیب، ابتدا باید توسط روشهای اندازهگیری مساحت، مساحت کف اتاق خواب را به دست بیاوریم تا بتوانیم مناسبترین فرش را برای آن انتخاب کنیم.
مساحت چگونه بدست می آید ؟
مساحت یک محدوده، با توجه به شکل آن محاسبه میشود. مساحت یک شکل هندسی، معمولا از ضرب دو اندازه با یکای طول به دست میآید.
به عنوان مثال، مساحت یک مربع، برابر با ضرب اندازه یکی از ضلعهای آن در خودش است.
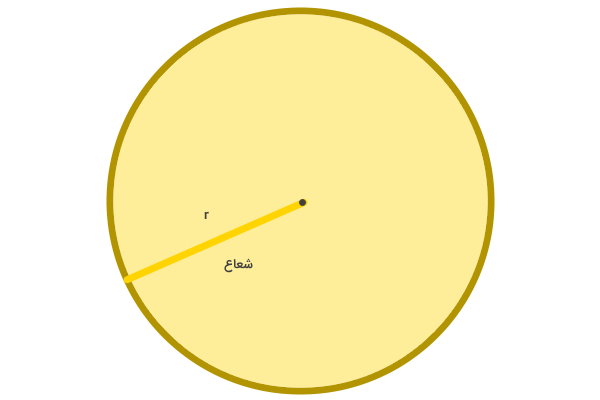
برای محاسبه مساحت برخی از شکلهای شناخته شده نظیر مثلث، مربع، مستطیل، دایره، لوزی، ذوزنقه و غیره، یک یا چند فرمول مخصوص وجود دارد. با این وجود، مساحت شکلهای نامنظم و پیچیده، با استفاده از روشهای غیر مستقیم و تخمینی تعیین میشود.
واحد مساحت چیست ؟
واحد مساحت، طول مربع است. به عنوان مثال، مساحت ایران برابر با ۱۶۴۸۱۹۵ کیلومتر مربع (حدود ۱/۶۴۸ میلیون کیلومتر مربع) یا ۶۳۶۳۷۲ مایل مربع است. در کشور ما، مساحت سطحهای مختلف بر اساس سیستم یکاهای بینالمللی یا «اِس آی» (SI) بیان میشود. جدول زیر، برخی از یکاهای مساحت در سیستم بینالمللی را نمایش میدهد.
| یکای مساحت در سیستم بینالمللی | نمایش ریاضی |
| میلیمتر مربع | mm۲ یا mm×mm |
| سانتیمتر مربع | cm۲ یا cm×cm |
| متر مربع | m۲ یا m×m |
| دکامتر مربع | dam۲ یا dam×dam |
| هکتومتر مربع | hm۲ یا hm×hm |
| کیلومتر مربع | km۲ یا km×km |
در سیستم آمریکایی، مساحت با یکاهایی نظیر اینچ مربع، فوت مربع، یارد مربع، ایکر و غیره بیان میشود.
تبدیل واحد مساحت
در سیستم بینالمللی، مساحت معمولا با واحد متر مربع بیان میشود. جدول زیر، تبدیل واحدهای دیگر مساحت به این واحد را نمایش میدهد.
| یکای مساحت در سیستم بینالمللی | مساحت بر حسب متر مربع |
| ۱ میلیمتر مربع | ۱0-۶ متر مربع |
| ۱ سانتیمتر مربع | ۱0-۴ متر مربع |
| ۱ متر مربع | ۱ متر مربع |
| ۱ دکامتر مربع | ۱0۲ متر مربع |
| ۱ هکتومتر مربع | ۱0۴ متر مربع |
| ۱ کیلومتر مربع | ۱0۶ متر مربع |
| ۱ اینچ مربع | ۱0-۴ × ۶/۴۵ متر مربع |
| ۱ فوت مربع | ۱0-۲ × ۹/۲۹ متر مربع |
| ۱ یارد مربع | ۱0-۱ × ۸/۳۶ متر مربع |
| ۱ مایل مربع | ۱0۶ × ۲/۵۹ متر مربع |
| ۱ ایکر | ۴۰۴۶ متر مربع |
نماد مساحت چیست ؟
در روابط ریاضی، عبارت جبری مساحت معمولا با حرف انگلیسی A یا a نمایش داده میشود. نماد مساحت رویه شکلهای سهبعدی نیز، حرف انگلیسی S است.
جدول مساحت تمام شکل های هندسی
در این بخش، مساحت شکلهای هندسی شناخته شده را در قالب یک جدول آوردهایم.
| شکل هندسی | فرمول مساحت | توضیحات |
| مثلث |
h: ارتفاع b: قاعده | |
|
s: نصف محیط مثلث a: اندازه ضلع اول b: اندازه ضلع دوم c: اندازه ضلع سوم | ||
|
a: ضلع اول b: ضلع دوم C: زاویه بین ضلع اول و دوم | ||
| مثلث متساوی الاضلاع | a: اندازه ضلع | |
| h: اندازه ارتفاع | ||
| مربع | a: اندازه ضلع | |
| مستطیل | l: طول
w: عرض | |
| لوزی |
p: یکی از قطرها q: قطر دیگر | |
| متوازیالاضلاع |
b: قاعده h: ارتفاع | |
| ذوزنقه |
a: اندازه یکی از قاعدهها b: اندازه قاعده دیگر h: اندازه ارتفاع | |
| چندضلعی منتظم |
a: ارتفاع چند ضلعی منتظم P: محیط چند ضلعی منتظم برابر با | |
| دایره |
r: شعاع | |
| بیضی |
a: شعاع بزرگ b: شعاع کوچک | |
| شکلهای نامنظم | مثلثبندی |
- |
| مکعب مستطیل |
l: طول وجوه بالایی و پایینی w: عرض وجوه بالایی و پایینی h: ارتفاع بین دو وجه بالایی و پایینی | |
| مکعب مربع |
a: اندازه ضلع | |
| منشور |
A: مساحت قاعده P: محیط قاعده H: ارتفاع منشور | |
| استوانه |
π: عدد ثابت ۳/۱۴ r: شعاع قاعده h: ارتفاع استوانه | |
| کره |
π: عدد ثابت ۳/۱۴ r: شعاع قاعده | |
| نیمکره |
π: عدد ثابت ۳/۱۴ r: شعاع قاعده | |
| هرم |
SB: مساحت قاعده P: محیط قاعده s: طول مایل یا ارتفاع وجه | |
| هرم ناقص |
SB۱: مساحت قاعده اول SB۲: مساحت قاعده دوم P۱: محیط قاعده اول P۲: محیط قاعده دوم s: ارتفاع وجه (طول مایل) | |
| مخروط |
π: عدد ثابت ۳/۱۴ r: شعاع قاعده l: طول یال | |
| مخروط ناقص |
π: عدد ثابت ۳/۱۴ r: شعاع قاعده کوچک R: شعاع قاعده بزرگ l: طول یال بین قاعده بزرگ و کوچک | |
| بیضیگون |
a: اندازه محور اول b: اندازه محور دوم c: اندازه محور سوم |
در ادامه، به معرفی هر یک از مساحتهای بالا و حل یک مثال برای هر کدام میپردازیم.
مساحت شکل های هندسی دو بعدی چیست ؟
شکلهای هندسی دوبعدی، شکلهایی هستند که میتوان آنها را بر روی یک سطح صاف رسم کرد. شکلهای دوبعدی، در دو جهت (دو بعد) گسترش دارند. دایره، مربع، مثلث و غیره، به عنوان شکلهای دوبعدی در نظر گرفته میشوند. در این بخش، نحوه محاسبه مساحت تمام شکلهای دوبعدی را به همراه مثال توضیح میدهیم.
مساحت مثلث چیست ؟
مثلث، شکلی است که از سه ضلع و سه راس تشکیل میشود. تصویر زیر، اجزای اصلی این شکل را نمایش میدهد. مساحت مثلث، از نصف حاصلضرب قاعده و ارتفاع به دست میآید. فرمول مساحت مثلث عبارت است از:
۲ ÷ (ارتفاع × قاعده) = مساحت مثلث
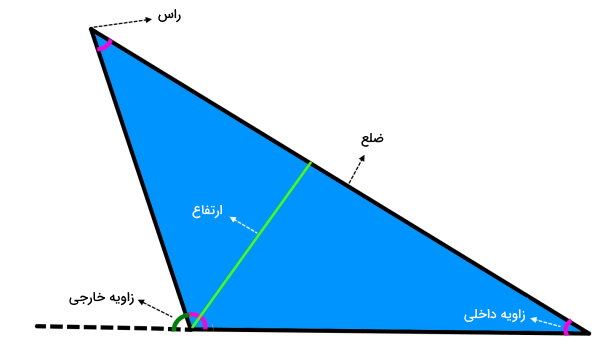
عبارت جبری مساحت مثلث به صورت زیر نوشته میشود:
- A: مساحت مثلث
- h: ارتفاع مثلث
- b: قاعده مثلث
مثلث، انواع مختلفی دارد. فرمول بالا، به عنوان فرمول اصلی برای محاسبه تمام مثلثها شناخته میشود. در صورتی که اندازه هر سه ضلع مثلث مشخص باشد، فرمول هرون به منظور محاسبه مساحت مورد استفاده قرار میگیرد:
- A: مساحت مثلث
- s: نصف محیط مثلث
- a: طول ضلع اول
- b: طول ضلع دوم
- c: طول ضلع سوم
در صورت مشخص بودن اندازه دو ضلع و زاویه بین آنها، مساحت مثلث از فرمول زیر به دست میآید:
- A: مساحت
- c: طول ضلع AB
- A: زاویه راس A
- B: زاویه راس B
- C: زاویه راس C (محاسبه با استفاده فرمول مجموع زوایای داخلی مثلث)
مثلث متساوی الاضلاع، یکی از انواع خاص مثلث است که سه ضلع و سه زاویه با اندازههای برابر دارد. اگر اندازه یکی از ضلعهای این مثلث مشخص باشد، مساحت آن با استفاده از فرمول زیر محاسبه میشود:
- A: مساحت مثلث متساوی الاضلاع
- a: اندازه ضلع مثلث متساوی الاضلاع
در صورت داشتن اندازه یکی از ارتفاعهای مثلث متساویالاضلاع نیز میتوان مساحت آن را توسط فرمول زیر تعیین کرد:
- A: مساحت مثلث متساوی الاضلاع
- h: اندازه ارتفاع مثلث متساوی الاضلاع
مثال ۱: محاسبه مساحت مثلث
اندازه ضلع یک مثلث متساویالاضلاع برابر با ۶ میلیمتر و اندازه ارتفاع آن برابر با ۵/۲ میلیمتر است. مساحت این مثلث را به دو روش حساب کنید.
در مثلث متساویالاضلع، اندازه تمام ضلعها با هم و اندازه تمام ارتفاعها با هم برابر است. ضلعهای مثلث، با عنوان قاعده نیز شناخته میشوند. به این ترتیب، اندازه سه ضلع (قاعدهها) و سه ارتفاع مثلث را داریم.
برای محاسبه مساحت، میتوانیم از روشهای مختلفی استفاده کنیم. اولین روش، استفاده از فرمول اصلی مساحت مثلث (با ارتفاع و قاعده) است. بر این اساس، مساحت مثلث مورد سوال به صورت زیر محاسبه میشود:
۲ ÷ (ارتفاع × قاعده) = مساحت مثلث
۲ ÷ (۵/۲× ۶) = مساحت مثلث
۲ ÷ (۳۱/۲) = مساحت مثلث
۱۵/۶ = مساحت مثلث
مساحت مثلث برابر با ۱۵/۶ میلیمتر مربع است. با توجه به اطلاعات مسئله، امکان استفاده از فرمولهای هرون، سینوس و فرمولهای مخصوص مثلث متساویالاضلاع وجود دارد. در اینجا، از فرمول مساحت مثلث متساویالاضلاع با ارتفاع استفاده میکنیم:
- A: مساحت مثلث متساوی الاضلاع
- h: اندازه ارتفاع مثلث متساوی الاضلاع برابر با ۵/۲
در نتیجه، مساحت مثلث برابر با ۱۵/۶۱ میلیمتر مربع است.
به منظور آشنایی بیشتر با مباحث مربوط به محاسبه مساحت انواع مثلثها، مطالعه مطالب موجود در مجموعه مقالات «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمولها» را به شما پیشنهاد میکنیم.
مساحت مربع چیست ؟
مربع، یک چندضلعی منتظم است که از چهار ضلع هماندازه و چهار زاویه قائمه (۹۰ درجه) تشکیل میشود. مساحت مربع از ضرب اندازه یکی از ضلعهای آن در خودش به دست میآید. فرمول مساحت مربع عبارت است از:
خودش × اندازه یک ضلع = مساحت مربع

عبارت جبری مساحت مربع به صورت زیر نوشته میشود:
- A: مساحت مربع
- a: اندازه یکی از ضلعهای مربع
فرمول بالا را میتوان به صورت توانی نیز بازنویسی کرد:
البته مساحت مربع با استفاده از اندازه قطر آن نیز به دست میآید. فرمول مساحت مربع با قطر عبارت است از:
- A: مساحت مربع
- d: اندازه قطر مربع
مثال ۲: محاسبه مساحت مربع
مساحت مربعی به ضلع ۴ سانتیمتر را به دست بیاورید.
به منظور تعیین مساحت مربع، اندازه یکی از ضلعهای آن را در خودش ضرب میکنیم:
خودش × اندازه یک ضلع = مساحت مربع
اندازه یک ضلع مربع برابر با ۴ سانتیمتر است. این اندازه را درون رابطه بالا قرار میدهیم:
۴ × ۴ = مساحت مربع
۱۶ = مساحت مربع
در نتیجه، مساحت مربع برابر با ۱۶ سانتیمتر مربع است. به منظور آشنایی کامل با مباحث مربوط به محاسبه مساحت مربع، مطالعه مطالب موجود در مجموعه مقالات «محاسبه محیط و مساحت مربع — تمامی فرمولها» را به شما پیشنهاد میکنیم.
مساحت مستطیل چیست ؟
مستطیل، یکی دیگر از شناخته شدهترین چهارضلعیها است. مستطیل نیز مانند مربع، از چهار زاویه قائمه تشکیل میشود. در این شکل، ضلعهای روبهرویی با هم مساوی و موازی هستند. به ضلعهای بزرگ مستطیل، طول و به ضلعهای کوچک آن، عرض میگویند. مساحت مستطیل از ضرب طول و عرض آن در یکدیگر به دست میآید. فرمول مساحت مستطیل عبارت است از:
عرض × طول = مساحت مستطیل
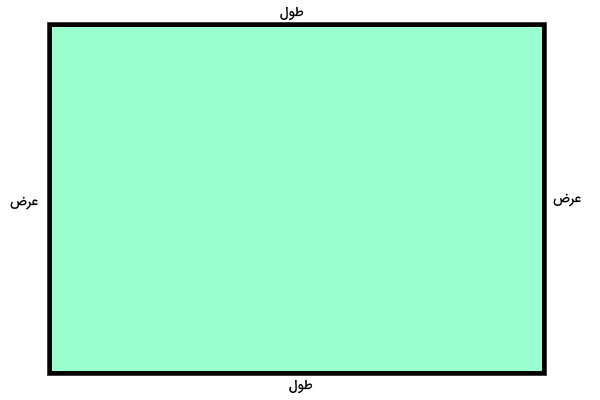
عبارت جبری مساحت مستطیل به صورت زیر نوشته میشود:
- A: مساحت مستطیل
- l: طول مستطیل
- w: عرض مستطیل
مساحت مستطیل، با استفاده از اندازه قطر آن نیز به دست میآید. به این منظور، باید اندازه قطر و یکی از ضلعهای مستطیل را داشته باشیم. فرمول مساحت مستطیل با قطر عبارت است از:
یا
- A: مساحت مستطیل
- l: طول مستطیل
- w: عرض مستطیل
- d: قطر مستطیل
مثال ۳: محاسبه مساحت مستطیل
اندازه دو ضلع یک مستطیل برابر با ۶ و ۵ متر است. مساحت این مستطیل را حساب کنید.
ضلعهای ۶ و ۵ متری، به ترتیب طول و عرض مستطیل محسوب میشوند. با ضرب اندازه این ضلعها در یکدیگر، مساحت مستطیل به دست میآید:
عرض × طول = مساحت مستطیل
۵ × ۶ = مساحت مستطیل
۳۰ = مساحت مستطیل
در نتیجه، مساحت مستطیل برابر با ۳۰ متر مربع است.
مثال ۴: مقایسه مساحت مربع و مستطیل
مربع و مستطیل زیر را در نظر بگیرید. اندازه ضلعهای این دو شکل در کنارشان نوشته شده است. مساحت هر شکل را تعیین کرده و مقادیر به دست آمده را با هم مقایسه کنید.
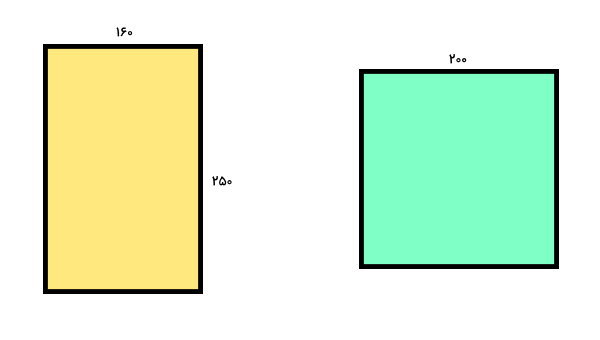
در تصویر بالا، اندازه یکی از ضلعهای مربع داده شده است. همین اندازه برای محاسبه مساحت مربع کفایت میکند؛ چراکه برای مساحت این شکل داریم:
- AS: مساحت مربع
- a: اندازه یکی از ضلعهای مربع برابر با ۲۰۰
اندازه ضلع را به جای a درون فرمول بالا قرار میدهیم و آن را حل میکنیم:
مساحت مربع برابر با ۴۰۰۰۰ واحد سطح است. برای مساحت مستطیل نیز داریم:
- AR: مساحت مستطیل
- l: طول مستطیل برابر با ۲۵۰
- w: عرض مستطیل برابر با ۱۶۰
مساحت مستطیل برابر با ۴۰۰۰۰ واحد سطح است. در نتیجه، این دو شکل، مساحتهای برابر دارند. به منظور آشنایی کامل با مباحث مربوط به محاسبه مساحت مستطیل، مطالعه مطالب موجود در مجموعه مقالات «آموزشهای بدست آوردن محیط و مساحت مستطیل + حل تمرین و تمامی فرمولها» را به شما پیشنهاد میکنیم.
مساحت لوزی چیست ؟
لوزی، یک نوع چهارضلعی با اندازه ضلعهای برابر است. در صورت قائمه بودن زاویههای داخلی این شکل، به آن مربع میگویند. مساحت لوزی معمولا با استفاده از اندازه قطرها به دست میآید. مساحت لوزی برابر با حاصلضرب قطر کوچک و بزرگ تقسیم بر دو است. فرمول مساحت لوزی عبارت است از:
۲ ÷ (قطر کوچک × قطر بزرگ) = مساحت لوزی
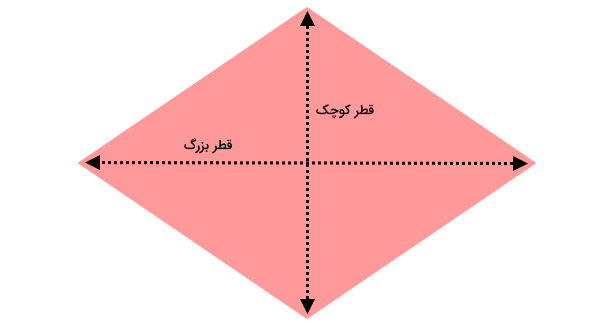
عبارت جبری مساحت لوزی به صورت زیر نوشته میشود:
- A: مساحت لوزی
- p: یکی از قطرهای لوزی
- q: قطر دیگر لوزی
مثال ۵: محاسبه مساحت لوزی
اگر اندازه قطرهای یک لوزی برابر با ۵/۵ و ۱۴ سانتیمتر باشد، مساحت آن چقدر خواهد بود؟
مساحت لوزی، نصف حاصلضرب قطر بزرگ (۱۴) و قطر کوچک (۵/۵) است. با قرار دادن این اندازهها درون فرمول زیر، به این مساحت میرسیم:
۲ ÷ (قطر کوچک × قطر بزرگ) = مساحت لوزی
۲ ÷ (۵/۵ × ۱۴) = مساحت لوزی
۲ ÷ (۷۷) = مساحت لوزی
۳۸/۵ = مساحت لوزی
در نتیجه، مساحت لوزی برابر با ۳۸/۵ سانتیمتر مربع است. به منظور آشنایی کامل با مباحث مربوط به محاسبه مساحت لوزی، مطالعه مطالب موجود در مجموعه مقالات «محاسبه محیط و مساحت لوزی — تمامی فرمولها» را به شما پیشنهاد میکنیم.
مساحت ذوزنقه چیست ؟
ذوزنقه، یک شکل چهارضلعی است که از دو ضلع موازی و دو ضلع غیر موازی تشکیل میشود. به ضلعهای موازی این شکل، قاعده و به ضلعهای غیر موازی آن، ساق میگویند. فاصله عمودی بین دو قاعده، ارتفاع نام دارد. مساحت ذوزنقه برابر با نصف مجموع قاعدهها ضربدر ارتفاع است:
ارتفاع × (۲ ÷ مجموع قاعده بزرگ و کوچک) = مساحت ذوزنقه
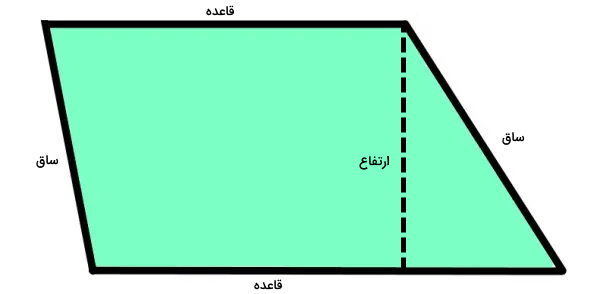
عبارت جبری مساحت ذوزنقه به صورت زیر نوشته میشود:
- A: مساحت ذوزنقه
- a: اندازه یکی از قاعدهها
- b: اندازه قاعده دیگر
- h: اندازه ارتفاع
مثال ۶: محاسبه مساحت ذوزنقه
مساحت یک ذوزنقه برابر با ۱۰۸۰ واحد سطح است. اگر اندازه ضلعهای موازی آن برابر با ۵۵/۶ و ۳۴/۴ واحد طول باشد، فاصله عمودی بین قاعدههای آن چقدر خواهد بود؟
ضلعهای موازی ذوزنقه، به عنوان قاعدههای آن در نظر گرفته میشوند. فاصله عمودی بین دو قاعده نیز همان ارتفاع ذوزنقه است. با توجه به اطلاعات مسئله، به منظور محاسبه ارتفاع، میتوانیم از فرمول زیر استفاده کنیم:
ارتفاع × (۲ ÷ مجموع قاعده بزرگ و کوچک) = مساحت ذوزنقه
ارتفاع × [۲ ÷ (۳۴/۴+۵۵/۶)] = ۱۰۸۰
ارتفاع × [۲ ÷ ۹۰] = ۱۰۸۰
ارتفاع × ۴۵ = ۱۰۸۰
۴۵ ÷ ۱۰۸۰ = ارتفاع
۱۲ = ارتفاع
در نتیجه، ارتفاع ذوزنقه برابر با ۱۲ واحد طول است.
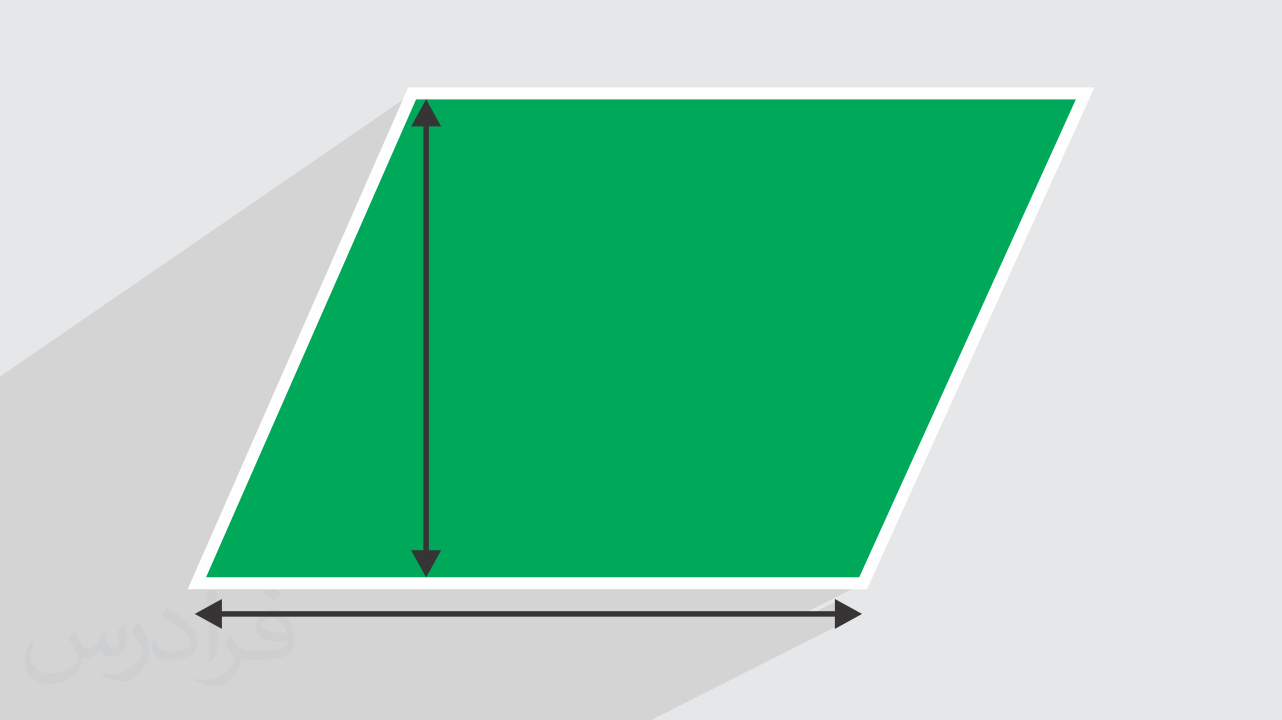
مساحت متوازی الاضلاع چیست ؟
متوازیالاضلاع، یک شکل چهارضلعی است که ضلعهای روبهرویی آن، مساوی و موازی هستند. به فاصله عمودی یک راس تا ضلع مقابلش، ارتفاع میگویند. در این حالت، ضلع مقابل به آن راس، قاعده نظیر ارتفاع محسوب میشود. مساحت متوازی الاضلاع از ضرب قاعده در ارتفاع نظیر به دست میآید:
ارتفاع × قاعده = مساحت متوازی الاضلاع
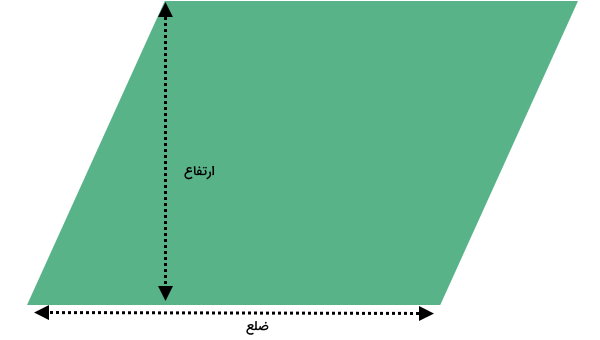
عبارت جبری مساحت متوازی الاضلاع به صورت زیر نوشته میشود:
- S: مساحت متوازیالاضلاع
- b: قاعده
- h: ارتفاع
روشهای متعددی برای محاسبه مساحت متوازیالاضلاع وجود دارد. در صورت دانستن اندازه دو ضلع مجاور و زاویه بین آنها و دو قطر و زاویه بین آنها، امکان تعیین مساحت متوازیالاضلاع فراهم میشود. علاوه بر این، به خاطر داشته باشید که لوزی، مربع و مستطیل، از انواع خاص متوازیالاضلاع به شمار میروند. بنابراین، فرمولهای مساحت متوازیالاضلاع برای این شکلها نیز قابل استفاده هستند.
مثال ۷: محاسبه مساحت متوازی الاضلاع
متوازیالاضلاع زیر را در نظر بگیرید. اگر اندازه ارتفاع h برابر با ۱۳۸ سانتیمتر و قاعده b برابر با ۱۲۰ سانتیمتر باشد، مساحت متوازیالاضلاع چند متر مربع خواهد بود؟
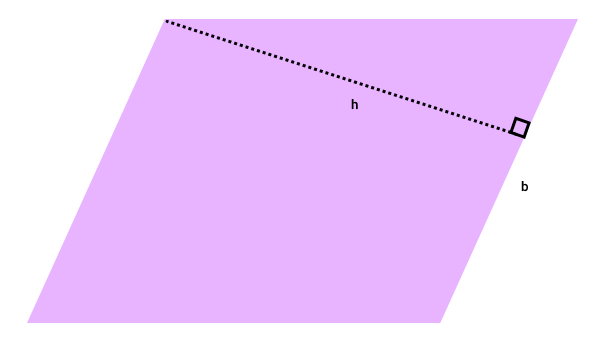
در صورت سوال، اندازه ارتفاع و قاعده بر حسب سانتیمتر داده شده اما مساحت با واحد متر مربع خواسته شده است. برای اینکه بتوانیم مساحت را بر حسب متر مربع به دست بیاوریم، ابتدا باید اندازههای مورد نیاز را به واحد متر تبدیل کنیم. فرمول مساحت متوازیالاضلاع عبارت است از:
- S: مساحت متوازیالاضلاع
- b: قاعده برابر با ۱۲۰ سانتیمتر
- h: ارتفاع برابر با ۱۳۸ سانتیمتر
بر اساس قواعد تبدیل واحد داریم:
۱ متر = ۱۰۰ سانتیمتر
بنابراین:
- b: قاعده برابر با ۱/۲۰ متر
- h: ارتفاع برابر با ۱/۳۸ متر
اندازههای بالا را درون فرمول مساحت قرار میدهیم:
در نتیجه، مساحت متوازیالاضلاع برابر با ۱/۶۵۶ متر مربع است.
به منظور آشنایی کامل با مباحث مربوط به محاسبه مساحت متوازیالاضلاع، مطالعه مطالب موجود در مجموعه مقالات «محاسبه محیط و مساحت متوازی الاضلاع — هر آنچه باید بدانید» از مجله فرادرس را به شما پیشنهاد میکنیم.
مساحت چندضلعی منتظم چیست ؟
چندضلعی منتظم، به چندضلعی گفته میشود که ضلعها و زاویههای هماندازه دارد. مثلث متساویالاضلاع و مربع، از شناخته شدهترین چندضلعیهای منتظم هستند. در بخشهای قبلی، راجع به محاسبه مساحت این دو شکل صحبت کردیم. با این وجود، مساحت چندضلعیهای منتظم دیگر نظیر پنجضلعی منتظم، ششضلعی منتظم و غیره، توسط یک فرمول خاص به دست میآید. مساحت چندضلعی منتظم برابر با نصف حاصلضرب محیط در ارتفاع است:
۲ ÷ (محیط × ارتفاع) = مساحت ذوزنقه
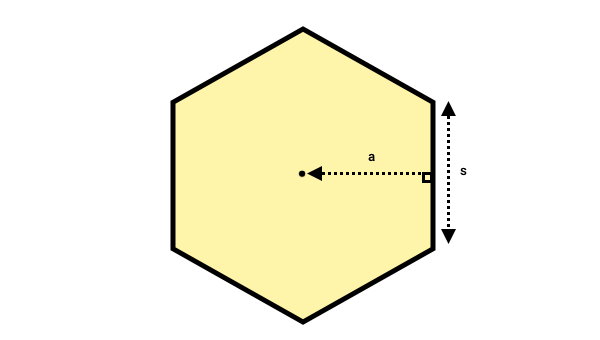
عبارت جبری مساحت چندضلعی منتظم به صورت زیر نوشته میشود:
- A: مساحت چند ضلعی منتظم
- a: ارتفاع چند ضلعی منتظم
- P: محیط چند ضلعی منتظم برابر با
- n: تعداد ضلعها
- s: اندازه هر ضلع
امکان محاسبه مساحت چندضلعیهای منتظم با استفاده از فرمول زیر نیز وجود دارد:
- A: مساحت چندضلعی منتظم
- n: تعداد ضلعها
- s: اندازه هر ضلع
با استفاده از فرمول بالا میتوان رابطه مخصوص مساحت هر یک از چندضلعیهای منتظم را به صورت جداگانه نوشت. به عنوان مثال، با توجه به فرمول بالا، فرمول مساحت ششضلعی منتظم برابر میشود با:
- A: مساحت چندضلعی منتظم
- s: اندازه هر ضلع
مثال ۸: محاسبه مساحت چندضلعی منتظم
مساحت یک نهضلعی منتظم به ضلع ۷ متر و ارتفاع ۹/۶ متر را به دست بیاورید.
مساحت نهضلعی منتظم برابر است با:
- A: مساحت نهضلعی منتظم
- a: ارتفاع نهضلعی منتظم برابر با ۹/۶ متر
- P: محیط نهضلعی منتظم
محیط چندضلعی منتظم، از ضرب اندازه یکی از ضلعهای آن در تعداد ضلعها به دست میآید. بنابراین داریم:
۹ × اندازه ضلع = محیط نهضلعی منتظم
۹ × ۷ = محیط نهضلعی منتظم
۶۳ = محیط نهضلعی منتظم
این اندازه را در فرمول مساحت قرار میدهیم:
در نتیجه، مساحت نهضلعی منتظم برابر با ۳۰۲/۴ متر مربع است. به منظور آشنایی کامل با مباحث مربوط به محاسبه مساحت انواع چندضلعیها، مطالعه مطالب موجود در مجموعه مقالات «آموزش انواع چند ضلعیها — تعاریف و تمامی فرمولهای محیط و مساحت» را به شما پیشنهاد میکنیم.
مساحت دایره چیست ؟
دایره، یک منحنی بسته است. تمام نقاط دایره، از یک نقطه ثابت درون آن به یک اندازه فاصله دارند. به این فاصله شعاع میگویند. مساحت دایره، با استفاده از اندازه شعاع و ثابتی با عنوان عدد پی محاسبه میشود.
بر این اساس، فرمول مساحت دایره عبارت است از:
شعاع × شعاع × عدد پی = مساحت دایره
شعاع × شعاع × ۳/۱۴ = مساحت دایره
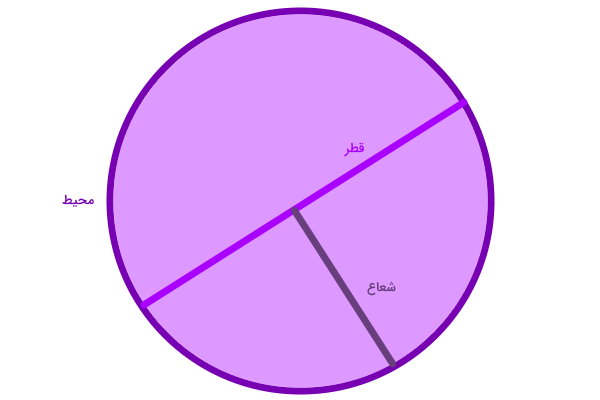
عبارت جبری مساحت دایره به صورت زیر نوشته میشود:
یا
قطاعهای دایره (نیمدایره، ربعدایره و غیره)، بخشی از یک دایره کامل هستند. بنابراین، مساحت این شکلهای هندسی نیز نسبتی از مساحت یک دایره کامل خواهد بود.

مساحت قطاع دایره از فرمول زیر به دست میآید:
- A: مساحت قطاع
- r: شعاع
- α: زاویه مرکزی بر حسب رادیان
مثال ۹: محاسبه مساحت ربع دایره
ربعدایره، شکلی است که از تقسیم دایره به چهار قسمت مساوی تشکیل میشود. تصویر زیر، یک ربعدایره جدا شده از دایره کامل را نمایش میدهد. اگر شعاع دایره برابر با ۳ سانتیمتر باشد، مساحت ربعدایره چقدر خواهد بود؟
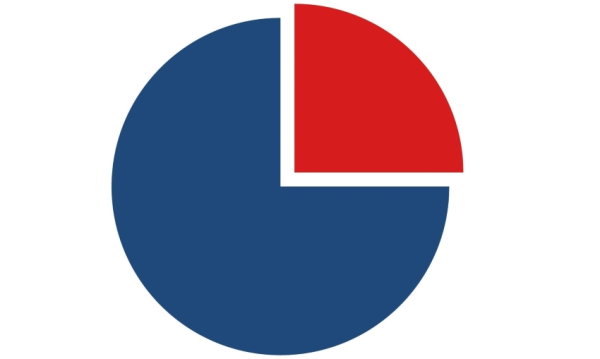
مساحت ربعدایره، یکچهارم مساحت دایره کامل است. به عبارت دیگر:
۴ ÷ مساحت دایره = مساحت ربع دایره
بنابراین، به منظور محاسبه مساحت ربعدایره، ابتدا باید مساحت دایره کامل را به دست بیاوریم:
شعاع × شعاع × عدد پی = مساحت دایره
شعاع دایره برابر با ۳ سانتیمتر و عدد پی، همواره برابر با ۳/۱۴ است:
۳ × ۳ × ۳/۱۴ = مساحت دایره
۹ × ۳/۱۴ = مساحت دایره
۲۸/۲۶ = مساحت دایره
به این ترتیب داریم:
۴ ÷ ۲۸/۲۶ = مساحت ربع دایره
۷/۰۶ = مساحت ربع دایره
در نتیجه، مساحت ربعدایره برابر با ۷/۰۶ است. به منظور آشنایی کامل با مباحث مربوط به محاسبه مساحت دایره، مطالعه مطالب موجود در مجموعه مقالات «آموزشهای بدست آوردن محیط و مساحت دایره + حل تمرین و تمامی فرمولها» را به شما پیشنهاد میکنیم.
مساحت بیضی چیست ؟
بیضی، منحنی بستهای است که مجموع فواصل تمام نقاط آن با دو نقطه ثابت درون آن، همواره یک عدد ثابت میشود. دایره، حالت خاصی از بیضی است. مساحت بیضی، از ضرب اندازه شعاع کوچک و بزرگ در عدد پی به دست میآید:
شعاع کوچک × شعاع بزرگ × ۳/۱۴ = مساحت بیضی
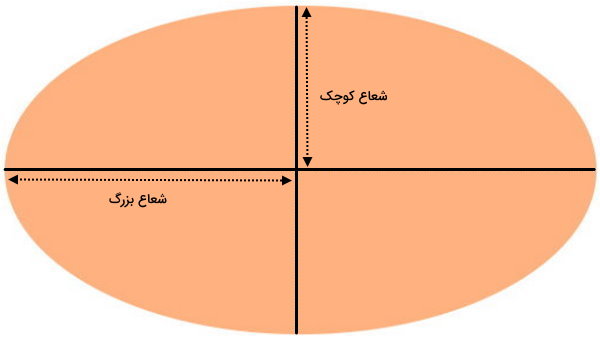
عبارت جبری مساحت بیضی به صورت زیر نوشته میشود:
- S: مساحت بیضی
- π: عدد ثابت ۳/۱۴
- a: شعاع بزرگ یا نصف محور اصلی
- b: شعاع کوچک یا نصف محور فرعی
مثال ۱۰: محاسبه مساحت بیضی
اندازه قطرهای یک بیضی برابر با ۳۰ و ۴۰ میلیمتر است. مساحت این بیضی را حساب کنید.
منظور از قطرهای بیضی، همان محورهای اصلی و فرعی است. مساحت بیضی از فرمول زیر به دست میآید:
- S: مساحت بیضی
- π: عدد ثابت ۳/۱۴
- a: شعاع بزرگ
- b: شعاع کوچک
شعاع بزرگ، نصف محور اصلی و برابر با ۲۰ است. شعاع کوچک نیز نصف محور فرعی و برابر با ۱۵ است. این مقادیر را در رابطه بالا قرار میدهیم و آن را حل میکنیم:
در نتیجه، مساحت بیضی برابر با ۹۴۲ میلیمتر مربع است.
مساحت شکل های نامنظم چیست ؟
در بخشهای قبلی، نحوه محاسبه مساحت شکلهای منظم را مورد بررسی قرار دادیم. برخی از این شکلها (مانند مثلث متساویالاضلاع)، منتظم و برخی دیگر (مانند ذوزنقه)، غیر منتظم بودند. در دنیای واقعی، سطح تمام اجسام همیشه به صورت منظم نیست. در این موارد، فرمول مخصوصی برای محاسبه مساحت وجود ندارد. به همین دلیل، باید از روشهای غیر مستقیم نظیر تقسیمبندی یا شبکهبندی استفاده کنیم.
تعیین مساحت شکلهای نامنظم به روش تقسیمبندی
تصویر زیر یک شکل چندضلعی نامنظم را نمایش میدهد. میخواهیم مساحت این شکل را به صورت غیر مستقیم به دست بیاوریم. متداولترین روش برای انجام این کار، تقسیم شکل نامنظم به مجموعهی از چندضلعیهای شناخته شده نظیر مثلث، مربع، مستطیل، متوازیالاضلاع و غیره است.

هیچ قاعده خاصی برای تقسیمبندی شکلهای نامنظم وجود ندارد. به عنوان مثال، در تصویر زیر، شکل نامنظم بالا به شکل مجموعهای از چند مثلث، مربع و متوازیالاضلاع درآمده است.
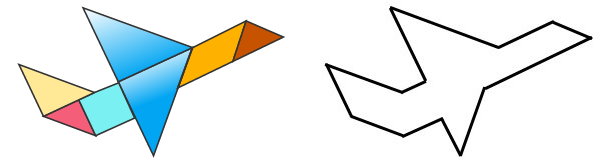
پس از تقسیمبندی شکل به شکلهای کوچکتر، امکان محاسبه مساحت فراهم میشود. مساحت این شکل، از جمع مساحتهای شکلهای درون آن به دست میآید. یکی از معروفترین روشهای تقسیم چندضلعیهای نامنظم برای به دست آوردن مساحت آنها، روش مثلثبندی است. به خاطر داشته باشید که تمام چندضلعیها را میتوان به صورت مجموعهای از مثلثها نمایش داد. جمع مساحتهای این مثلثها برابر با مساحت چندضلعی است.
تعیین مساحت شکلهای نامنظم به روش شبکهبندی
در برخی از مواقع، امکان تقسیمبندی شکلهای نامنظم به مجموعهای از چندضلعیهای شناخته شده وجود ندارد. در این حالت، بهترین روش، شبکهبندی سطح است. به عنوان مثال، تصویر زیر، شکل یک برگ را نمایش میدهد. ما نمیتوانیم مساحت این شکل را با استفاده از فرمول یا حتی تقسیمبندی آن به چندضلعیها به دست بیاوریم. به همین دلیل، یک شبکه مربعی بر روی آن رسم میکنیم.
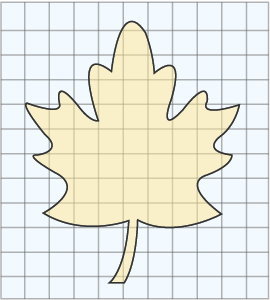
اگر حداقل نصف یک مربع درون شکل قرار داشته باشد، آن را به عنوان یک واحد در نظر میگیریم. در انتها، تعداد واحدهای درون شکل را با هم جمع میکنیم. مساحت تقریبی شکل، از ضرب تعداد واحدها در مساحت مربع به دست میآید.
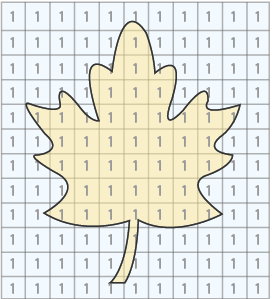
در روش تقسیمبندی چندضلعیهای نامنظم، امکان محاسبه دقیق مساحت وجود دارد. در طرف مقابل، روش شبکهبندی، مقدار تقریبی مساحت شکلهای نامنظم را به دست میآورد.
مثال ۱۱: محاسبه مساحت شکل نامنظم
مساحت شکل زیر را به دست بیاورید.
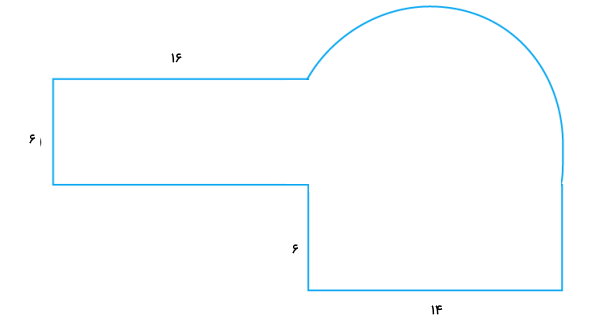
شکل بالا، یک شکل نامنظم است. به منظور محاسبه مساحت این شکل، آن را به مجموعهای از چندین شکل منظم تقسیم میکنیم. با این کار، شکل اولیه به دو مستطیل، یک مثلث قائمالزاویه و یک نیمدایره تقسیم میشود.
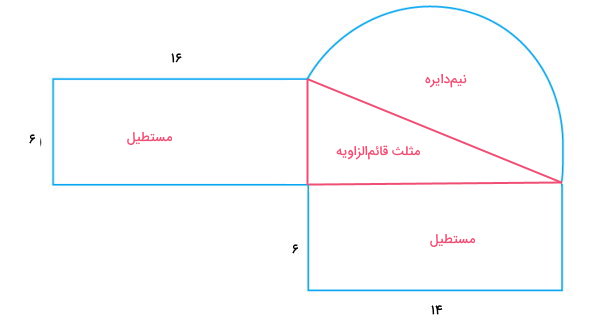
با جمع مساحت چهار شکل بالا، مساحت شکل نامنظم به دست میآید. به این ترتیب داریم:
نیمدایره + مثلث قائمالزاویه + مستطیل ۲ + مستطیل ۱ = مساحت کل
مساحت مستطیل ۱ و ۲، حاصلضرب طول در عرض آنها است:
۹۶ = ۶ × ۱۶ = مساحت مستطیل ۱
۸۴ = ۶ × ۱۴ = مساحت مستطیل ۲
از روی شکل تقسیمبندی میتوان مشاهده کرد که ساقهای مثلث قائمالزاویه برابر با ۶ و ۱۴ هستند. مساحت مثلثهای قائمالزاویه، برابر با نصف حاصلضرب ساقها است:
۴۲ = ۲ ÷ (۶ × ۱۴) = مساحت مثلث قائمالزاویه
اکنون، فقط به اندازه مساحت نیمدایره نیاز داریم تا بتوانیم مساحت کل شکل را محاسبه کنیم. از روی شکل میتوانیم ببینیم که قطر نیمدایره، وتر مثلثقائمالزاویه است. وتر مثلث قائمالزاویه از قضیه فیثاغورس به دست میآید:
- c: وتر مثلث قائمالزاویه
- a: اندازه یکی از ساقها برابر با ۶
- b: اندازه ساق دیگر برابر با ۱۴
اندازه وتر مثلث قائمالزاویه یا همان قطر نیمدایره برابر با ۱۵/۲۳ است. مساحت نیمدایره با استفاده از رابطه زیر تعیین میشود:
۲ ÷ مساحت دایره کامل = مساحت نیمدایره
مساحت دایره کامل برابر است با:
شعاع × شعاع × ۳/۱۴ = مساحت دایره
به جای شعاع در رابطه بالا، نصف اندازه قطر (۷/۶۱) را قرار میدهیم:
۷/۶۱ × ۷/۶۱ × ۳/۱۴ = مساحت دایره
۱۸۲/۱ = مساحت دایره
بنابراین، داریم:
۲ ÷ ۱۸۲/۰۸ = مساحت نیمدایره
۹۱/۰۴ = مساحت نیمدایره
در نهایت، تمام مساحتهای به دست آمده را با هم جمع میکنیم تا مساحت کل شکل به دست بیاید:
۹۱/۰۴ + ۴۲ + ۸۴ + ۹۶ = مساحت کل
۳۱۳/۰۴ = مساحت کل
در نتیجه، مساحت شکل نامنظم برابر با ۳۱۳/۰۴ واحد سطح است.
دیگر روش های محاسبه مساحت شکلهای دوبعدی
روشهای محاسبه مساحت شکلهای دوبعدی منظم و نامنظم، به موارد اشاره شده در بخشهای قبلی محدود نمیشوند. تا کنون، فرمولها و رویکردهای مختلفی برای این منظور توسعه یافتهاند. تقسیمبندی شکلهای پیچیده و نامنظم به شکلهای ساده و منظم، یکی از این رویکردها بود که به توضیح آن پرداختیم. از دیگر روشهای محاسبه مساحت شکلهای دوبعدی میتوان به موارد زیر اشاره کرد:
- «قانون نقطه میانی» (Midpoint Ordinate Rule)
- «قانون مختصات میانگین» (Average Ordinate Rule)
- «قانون سیمپسون» (Simpson's Rule)
- «قانون ذوزنقه» (Trapezoidal Rule)
روشهای بالا، اغلب در اندازهگیری مساحت زمین (فعالیتهای نقشهبرداری) مورد استفاده قرار میگیرند. مبنای این روشها، تخمین مساحت شکلهای نامنظم، با تقسیمبندی آنها به بخشهای کوچکتر است.
مساحت شکل های هندسی سه بعدی چیست ؟
مساحت رویه یا «مساحت سطح» (Surface Area)، اندازه فضایی است که توسط سطح بیرونی یک شکل سهبعدی پوشش داده میشود. مساحت رویه در اجسام سهبعدی چندوجهی، مجموع مساحتهای تمام وجهها است. در شکلهای کروی، این مساحت با اندازهگیری سطوح منحنی به دست میآید. در این بخش، به معرفی مساحت تمام شکلهای سهبعدی شناخته شده به همراه حل مثال میپردازیم.
مساحت مکعب مستطیل چیست ؟
مکعب مستطیل، یک شکل سهبعدی است که از شش وجه مستطیلی تشکیل میشود. تصویر زیر، یک مکعب مستطیل و وجههای آن را نمایش میدهد. وجههای این شکل را کنار یکدیگر قرار میدهیم. مساحت مکعب مستطیل، مجموع مساحت این وجهها (سطوح ۱ تا ۶) است.
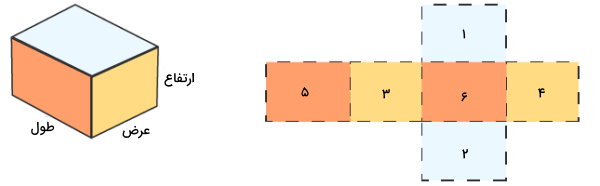
وجههای شمارهگذاری شده در تصویر بالا عبارت هستند از:
- مستطیل ۱ و ۲: وجههای بالایی و پایینی مکعب مستطیل
- مساحت هر مستطیل: عرض × طول
- مجموع مساحتها: (عرض × طول) × ۲
- مستطیل ۳ و ۴: وجههای جلو و عقب مکعب مستطیل
- مساحت هر مستطیل: ارتفاع × عرض
- مجموع مساحتها: (ارتفاع × عرض) × ۲
- مستطیل ۵ و ۶: وجههای چپ و راست مکعب مستطیل
- مساحت هر مستطیل: ارتفاع × طول
- مجموع مساحتها: (ارتفاع × طول) × ۲
به این ترتیب، مساحت مکعب مستطیل از فرمول زیر محاسبه میشود:
مجموع مستطیلها ۱ تا ۶ = مساحت مکعب مستطیل
(ارتفاع × طول) × ۲ + (ارتفاع × عرض) × ۲ + (عرض × طول) × ۲ =
(ارتفاع × طول + ارتفاع × عرض + عرض × طول) × ۲ =
عبارت جبری مساحت مکعب مستطیل برابر است با:
- S: مساحت کل مکعب مستطیل
- l: طول وجوه بالایی و پایینی
- w: عرض وجوه بالایی و پایینی
- h: ارتفاع بین دو وجه بالایی و پایینی
مساحت جانبی مکعب مستطیل چیست ؟
مساحت جانبی مکعب مستطیل، سطح وجههای قائم آن است. این مساحت از فرمول زیر به دست میآید:
(عرض + طول) × ارتفاع × ۲ = مساحت جانبی مکعب مستطیل
عبارت جبری رابطه بالا به صورت زیر نوشته میشود:
- Ss: مساحت جانبی مکعب مستطیل
- l: طول وجوه بالایی و پایینی
- w: عرض وجوه بالایی و پایینی
- h: ارتفاع بین دو وجه بالایی و پایینی
برای درک مفهوم مساحت جانبی، یک اتاق را در نظر بگیرید. مساحت کل اتاق، مجموع مساحت کل سطوح (کف، سقف و دیوارها) است. مساحت جانبی اتاق، مساحت دیوارهای آن را نمایش میدهد.
مثال ۱۲: محاسبه مساحت اتاق
طول و عرض یک اتاق مکعب مستطیلی، برابر با ۶ و ۴ متر است. اگر ارتفاع بین کف و سقف اتاق برابر با ۲/۵ متر باشد، مساحت کل اتاق چقدر خواهد بود؟
شکل اتاق، مکعب مستطیل است. بنابراین، مساحت کل اتاق (جمع مساحت چهار دیوار، سقف و کف)، از رابطه زیر به دست میآید:
- S: مساحت کل اتاق
- l: طول کف و سقف اتاق برابر با ۶ متر
- w: عرض کف و سقف اتاق برابر با ۴
- h: ارتفاع بین سقف و کف اتاق برابر با ۲/۵
اندازههای معلوم را درون فرمول قرار میدهیم:
در نتیجه، مساحت اتاق برابر با ۹۸ متر مربع است.
مساحت مکعب مربع چیست ؟
مکعب مربع، یک شکل سهبعدی است که از شش وجه مربعی هماندازه تشکیل میشود. مساحت مکعب مربع از جمع مساحت وجههای آن به دست میآید. به دلیل برابر بودن ابعاد تمام وجهها، این مساحت برابر است با:
مساحت یک وجه × ۶ = مساحت مکعب مربع
خودش × اندازه یک ضلع × ۶ = مساحت مکعب مربع
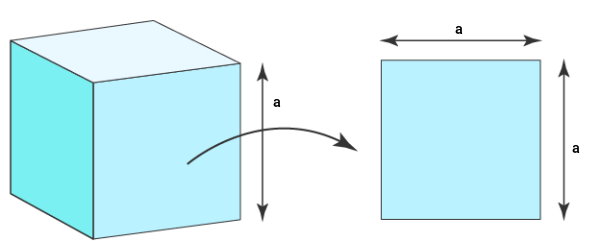
عبارت جبری مساحت مکعب مربع به صورت زیر نوشته میشود:
- S: مساحت کل مکعب مربع
- a: اندازه یک ضلع
مساحت جانبی مکعب مربع چیست ؟
مکعب مربع، چهار وجه جانبی هماندازه دارد. به این ترتیب، مساحت جانبی این شکل برابر است با:
- Ss: مساحت کل مکعب مربع
- a: اندازه یک ضلع
مثال ۱۳: محاسبه مساحت مکعب مربع
مساحت مکعب مربعی به ضلع ۷ سانتیمتر را محاسبه کنید.
مساحت کل وجههای مکعب مربع برابر است با:
- S: مساحت کل مکعب مربع
- a: اندازه یک ضلع برابر با ۷ سانتیمتر
مساحت مکعب مربع برابر با ۲۹۴ سانتیمتر مربع است.
مساحت منشور چیست ؟
منشور، یک نوع چندوجهی است که از دو قاعده چندضلعی مشابه تشکیل میشود. مساحت سطح منشور، از جمع مساحت وجههای جانبی و مساحت قاعدهها به دست میآید. منشور زیر را در نظر بگیرید. قاعدههای این منشور به شکل مثلث و وجههای جانبی آن به شکل مستطیل هستند.
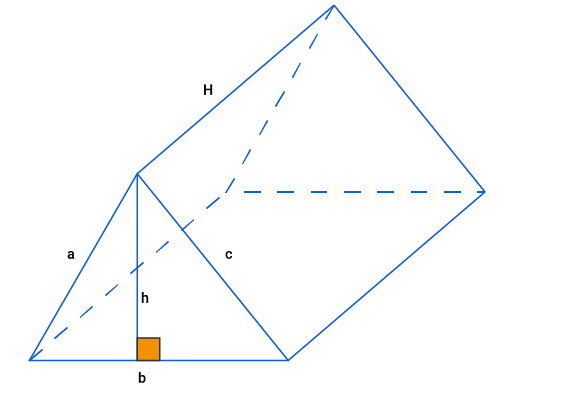
میخواهیم مساحت سطح منشور مثلثی بالا را تعیین کنیم. با توجه به شکل، داریم:
مساحت وجههای جانبی + مساحت قاعدهها = مساحت منشور مثلثی
عبارت جبری رابطه بالا را مینویسیم:
- S: مساحت سطح منشور
- SB: مساحت قاعدهها
- SL: مساحت وجههای جانبی
قاعدههای منشور، مثلثی هستند. فرمول مساحت مثلث، به صورت زیر نوشته میشود:
- A: مساحت مثلث
- b: قاعده مثلث
- h: ارتفاع مثلث
به دلیل برابر بودن قاعدههای منشور، برای SB داریم:
وجههای جانبی منشور، مستطیلی هستند. مساحت مستطیل از فرمول زیر به دست میآید:
- AR: مساحت مستطیل
- l: طول مستطیل
- w: عرض مستطیل
طول تمام مستطیلها برابر با H یا همان ارتفاع منشور است. هر یک از ضلعهای قاعده نیز به عنوان عرض مستطیلها در نظر گرفته میشوند. بنابراین برای SL داریم:
در رابطه بالا از H فاکتور میگیریم:
عبارت داخل پرانتز، محیط قاعده (مثلث) را نمایش میدهد:
به عبارت دیگر، مساحت وجههای جانبی منشور، برابر با حاصلضرب محیط قاعده در ارتفاع منشور است:
بر اساس روابط به دست آمده، میتوانیم فرمول مساحت منشور را به صورت زیر بازنویسی کنیم:
- S: مساحت سطح منشور
- A: مساحت قاعده
- P: محیط قاعده
- H: ارتفاع منشور
وجههای جانبی منشورهای قائم، همواره به شکل مستطیل و وجههای جانبی منشورهای مایل، همواره به شکل متوازیالاضلاع هستند. مساحت متوازیالاضلاع نیز مانند مساحت مستطیل، از ضرب ارتفاع (طول) در قاعده (عرض) به دست میآید. بنابراین، فرمول بالا برای به دست آوردن مساحت منشورهای قائم و مایل با هر قاعدهای قابل استفاده خواهد بود.
در محاسبه مساحت منشورها، آشنایی با فرمولهای محیط و مساحت چندضلعیها حرف اول را میزند. شکل قاعده منشور، تفاوتی را در فرمول کلی مساحت آن ایجاد نمیکند. با این وجود، به دست آوردن اندازه پارامترهای مورد نیاز، فقط با دانستن فرمولهای محیط و مساحت امکانپذیر میشود.

مثال ۱۴: محاسبه مساحت منشور مربعی
منشوری با قاعده مربع را در نظر بگیرید. اگر اندازه ضلع این مربع برابر با a و اندازه ارتفاع منشور نیز برابر با a باشد، مساحت سطح منشور بر حسب a چقدر خواهد بود؟
بر اساس فرمول مساحت سطح منشور داریم:
- S: مساحت سطح منشور
- A: مساحت قاعده مربعی
- P: محیط قاعده مربعی
- H: ارتفاع منشور برابر با a
مساحت مربع برابر است با:
- A: مساحت مربع
- a: اندازه ضلع مربع (قاعده)
محیط مربع از فرمول زیر به دست میآید:
- P: محیط مربع
- a: اندازه ضلع مربع
اندازههای معلوم را درون فرمول مساحت سطح منشور قرار میدهیم:
مساحت سطح منشور مربعی مورد سوال برابر با ۶a۲ شد.
مساحت استوانه چیست ؟
استوانه، شکلی مشابه منشور است؛ با این تفاوت که استوانه از قاعدههای دایرهای شکل تشکیل میشود. تصویر زیر، اجزای مختلف استوانه را نمایش میدهد. مساحت این شکل از جمع مساحت دو قاعده با مساحت سطح منحنی محدود یه این دو به دست میآید.
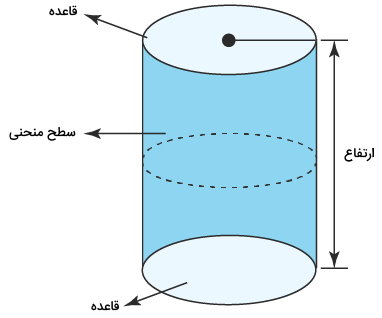
مساحت دایره را از بخشهای قبل میدانیم. مساحت سطح منحنی استوانه نیز از ضرب ارتفاع در محیط دایره به دست میآید. بنابراین، فرمول مساحت استوانه به صورت زیر نوشته میشود:
- S: مساحت سطح منشور
- π: عدد ثابت ۳/۱۴
- r: شعاع قاعده
مثال ۱۵: محاسبه مساحت سطح بشکه
بشکهای به قطر ۵۷ سانتیمتر و ارتفاع ۸۵ سانتیمتر را در نظر بگیرید. مساحت سطح این بشکه را حساب کنید.
بشکه، نمونهای از یک جسم استوانهای در دنیای واقعی است. از اینرو، مساحت رویه این جسم را میتوان با استفاده از فرمول زیر به دست آورد:
- S: مساحت سطح بشکه
- π: عدد ثابت ۳/۱۴
- r: شعاع قاعده بشکه برابر با ۲۸/۵=۲÷۵۷
- h: ارتفاع استوانه
مساحت رویه بشکه، تقریبا برابر با ۲۰۳۱۴ سانتیمتر مربع است.
مساحت کره چیست ؟
کره، یک شکل سهبعدی کاملا گرد است. تمام مقاطع دوبعدی کره، به شکل دایره در میآیند. مساحت کره، اندازه سطح رویه آن را نمایش میدهد. این مساحت برابر است با:
شعاع × شعاع × عدد پی × ۴ = مساحت کره
منظور از شعاع، فاصله نقاط روی کره تا مرکز آن است.
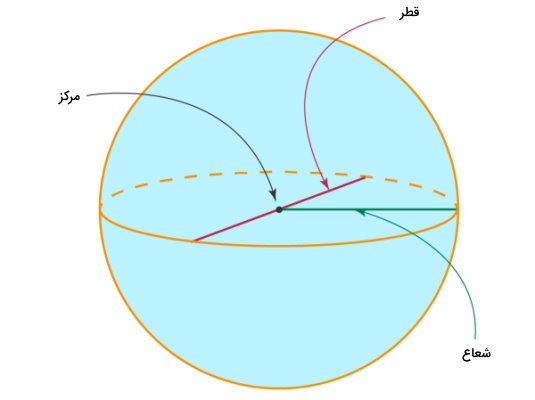
عبارت جبری مساحت کره به صورت زیر نوشته میشود:
- S: مساحت سطح کره
- π: عدد ثابت ۳/۱۴
- r: شعاع کره
مساحت سطح نیمکره، نصف مساحت کره کامل است. بنابراین، داریم:
- SH: مساحت سطح نیمکره
- π: عدد ثابت ۳/۱۴
- r: شعاع نیمکره
مثال ۱۶: محاسبه مساحت توپ فوتبال
قطر استاندارد توپهای فوتبال، معمولا حدود ۲۲ سانتیمتر است. مساحت سطح یک توپ فوتبال را به دست بیاورید.
توپ فوتبال، به شکل یک کره است. به منظور تعیین مساحت سطح این کره، از رابطه زیر استفاده میکنیم:
- S: مساحت سطح توپ
- π: عدد ثابت ۳/۱۴
- r: شعاع توپ برابر با ۱۱ سانتیمتر (نصف قطر توپ)
اندازههای معلوم را درون فرمول قرار میدهیم:
در نتیجه، مساحت رویه توپ فوتبال، تقریبا برابر با ۱۵۲۰ سانتیمتر است.
مساحت هرم چیست ؟
هرم، شکلی سهبعدی است که از یک قاعده و چند وجه جانبی تشکیل میشود. قاعده هرم میتواند به شکل مثلث، مربع دیگر چندضلعیها باشد. با این وجود، وجههای جانبی هرم، همواره به شکل مثلث هستند.
مساحت سطح هرم از جمع مساحت قاعده با مساحت وجههای جانبی به دست میآید.
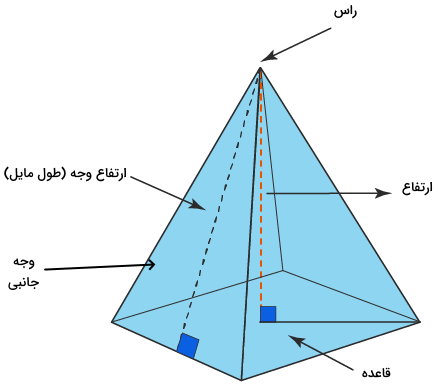
فرمول کلی مساحت سطح هرم به صورت زیر نوشته میشود:
- S: مساحت سطح هرم
- SB: مساحت قاعده
- SL: مساحت وجههای جانبی
به دلیل مثلثی بودن تمام وجههای جانبی هرم، مساحت آنها برابر است با:
- SL: مساحت وجههای جانبی
- P: محیط قاعده هرم
- s: طول مایل یا ارتفاع وجه جانبی
این رابطه با نوشتن فرمول مساحت تمام مثلثها و جمع آنها با یکدیگر اثبات میشود. مساحت قاعده هرم نیز به شکل آن بستگی دارد. بنابراین، فرمول مساحت سطح رویه به فرم زیر در میآید:
- S: مساحت هرم
- SB: مساحت قاعده
- P: محیط قاعده
- s: طول مایل یا ارتفاع وجه
مساحت هرم ناقص چیست ؟
با برداشتن بخشی از هرم کامل، هرم ناقص به وجود میآید. تصویر زیر، رابطه بین هرم کامل و ناقص را نمایش میدهد. همانطور که مشاهده میکنید، هرم ناقص، راسی ندارد و مانند منشورها از دو قاعده تشکیل میشود.
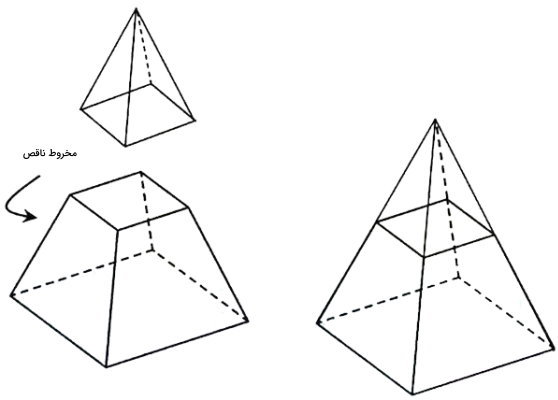
مساحت هرم ناقص از رابطه زیر به دست میآید:
- S: مساحت هرم ناقص
- SB۱: مساحت قاعده اول
- SB۲: مساحت قاعده دوم
- P۱: محیط قاعده اول
- P۲: محیط قاعده دوم
- s: ارتفاع وجه (طول مایل)
مثال ۱۷: محاسبه مساحت هرم
مساحت سطح یک هرم مربعی به ضلع ۹ و طول مایل ۲۰/۵ را تعیین کنید.
مساحت سطح هرم برابر است با:
- S: مساحت هرم
- SB: مساحت قاعده
- P: محیط قاعده
- s: طول مایل یا ارتفاع وجه برابر با ۲۰/۵
مساحت مربع از ضرب اندازه یک ضلع در خودش به دست میآید:
- SB: مساحت قاعده مربعی
- a: اندازه یک ضلع برابر با ۹
مساحت قاعده برابر با ۸۱ واحد سطح است. محیط قاعده با استفاده از فرمول زیر محاسبه میشود:
- P: محیط قاعده مربعی
- a: اندازه یک ضلع برابر با ۹
محیط قاعده برابر با ۳۶ واحد طول است. اکنون میتوانیم مساحت سطح هرم را حساب کنیم:
در نتیجه، مساحت رویه هرم برابر با ۴۵۰ واحد سطح است.
مساحت مخروط چیست ؟
مخروط، شکلی مشابه با هرم اما با قاعده دایره است. این شکل از دو سطح (قاعده دایرهای و وجه منحنی) تشکیل میشود.
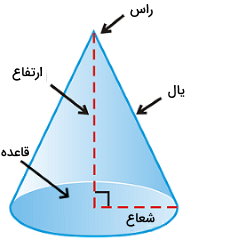
فرمول مساحت سطح مخروط عبارت است از:
- S: مساحت رویه مخروط
- π: عدد ثابت ۳/۱۴
- r: شعاع قاعده
- l: طول یال
با فاکتور گرفتن از عبارت πr، فرمول بالا به فرم ساده شده زیر در میآید:
مساحت مخروط ناقص چیست ؟
مخروط ناقص، بخشی از یک مخروط کامل است. این شکل از دو قاعده دایرهای و یک وجه منحنی تشکیل میشود.
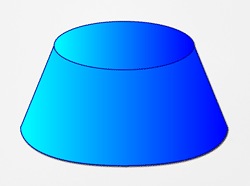
فرمول مساحت سطح مخروط ناقص عبارت است از:
- SF: مساحت رویه مخروط ناقص
- π: عدد ثابت ۳/۱۴
- r: شعاع قاعده کوچک
- R: شعاع قاعده بزرگ
- l: طول یال بین قاعده بزرگ و کوچک
مثال ۱۸: محاسبه مساحت مخروط
مساحت رویه مخروطی به شعاع قاعده ۷ اینچ و طول یال ۳ اینچ را بر حسب اینچ مربع و سانتیمتر مربع به دست بیاورید.
بر اساس فرمول مساحت مخروط، داریم:
- S: مساحت رویه مخروط
- π: عدد ثابت ۳/۱۴
- r: شعاع قاعده برابر با ۷ اینچ
- l: طول یال برابر با ۳ اینچ
مساحت رویه مخروط برابر با ۲۱۹/۸ اینچ مربع است. به منظور تعیین مساحت رویه بر حسب سانتیمتر مربع، چند روش وجود دارد. در سادهترین روش، میتوانیم ابتدا مقادیر داده شده به اینچ را به سانتیمتر تبدیل کنیم و آنها را درون فرمول مساحت قرار دهیم. بر اساس قواعد تبدیل واحد، هر ۱ اینچ برابر با ۲/۵۴ سانتیمتر است. بنابراین:
۱۷/۷۸ سانتیمتر = ۲/۵۴ × ۷ اینچ = شعاع قاعده
۷/۶۲ سانتیمتر = ۲/۵۴ × ۳ اینچ = طول یال
مساحت مخروط را با استفاده از این مقادیر حل میکنیم:
در نتیجه، مساحت رویه مخروط برابر با ۱۴۱۸/۰۶ سانتیمتر مربع است.
مساحت کره بیضوی یا بیضی گون چیست ؟
به کرهای که در یک یا چند راستا کشیده یا فشرده شده باشد، کره بیضوی یا بیضیگون میگویند. مساحت بیضیگون، با استفاده از اندازه شعاعهای آن به دست میآید. تصویر زیر، سه شعاع یک بیضیگون را نمایش میدهد.
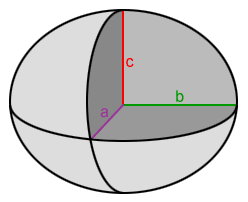
فرمول مساحت بیضیگون به صورت زیر نوشته میشود:
- S: مساحت رویه بیضیگون
- a: اندازه محور اول
- b: اندازه محور دوم
- c: اندازه محور سوم
تفاوت مساحت با دیگر کمیت های هندسی چیست ؟
مساحت، یکی از مفاهیم پرکاربرد در هندسه است. این کمیت معمولا با کمیتهای دیگری نظیر محیط، مساحت رویه و حجم مقایسه میشود. در این بخش، به معرفی تفاوتهای این مفاهیم هندسی میپردازیم.
تفاوت مساحت و محیط چیست ؟
محیط و مساحت، دو مفهوم هندسی کاملا متفاوت هستند. محیط، اندازه دور یک شکل هندسی دوبعدی را نمایش میدهد. مساحت، به عنوان اندازه سطح درون محیط در نظر گرفته میشود. واحد محیط، همان واحد طول (میلیمتر، سانتیمتر، متر و غیره) است. در صورتی که واحد مساحت، مربع واحد طول (میلیمتر مربع، سانتیمتر مربع، متر مربع و غیره) است.
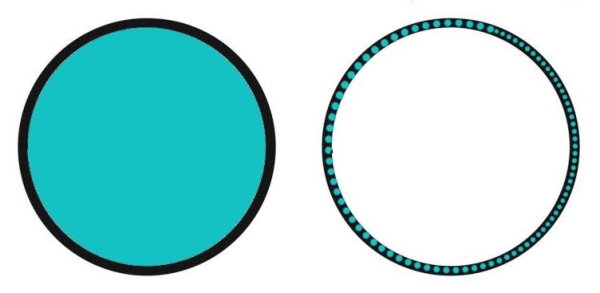
محیط و مساحت، از مفاهیم پرکاربرد هندسی به شمار میروند. به عنوان مثال، اگر بخواهیم مسافت پیادهروی دور یک پارک را به دست بیاوریم، از مفهوم محیط استفاده میکنیم. اما اگر بخواهیم بدانیم این پارک چه میزان از فضای سطح شهر را اشغال کرده است، از مفهوم مساحت استفاده میکنیم.
تفاوت مساحت با مساحت رویه چیست ؟
تفاوت اصلی بین مساحت و مساحت رویه این است که مساحت، به منظور توصیف فضای اشغال شده توسط یک شکل دوبعدی مورد استفاده قرار میگیرد؛ در حالیکه مساحت رویه، فضای اشغال شده توسط سطح بیرونی یک شکل سهبعدی را توصیف میکند. این دو مفهوم، کاربردهای زیادی در زندگی روزمره انسانها دارند.
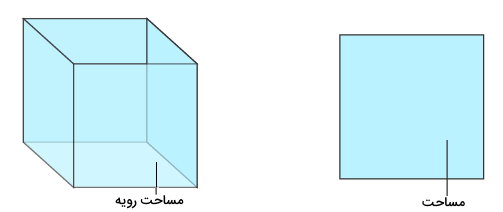
به عنوان مثال، اندازه یک زمین با استفاده از مساحت آن تعریف میشود. محاسبه میزان پارچه، کاغذ یا هر پوشش دیگر برای پوشاندن یک جعبه نیز توسط مساحت رویه انجام میگیرد. مساحت و مساحت رویه، شباهتهایی نیز با یکدیگر دارند. شباهت اصلی این دو، یکای آنها (سانتیمتر، متر مربع و غیره) است.
تفاوت مساحت و حجم چیست ؟
حجم، ظرفیت اجسام در فضای سهبعدی است. مساحت یک شکل دوبعدی، سطح پوشش داده شده توسط آن را نمایش میدهد؛ در صورتی که حجم یک شکل سهبعدی، به عنوان فضای اشغال شده توسط آن تعریف میشود. حجم اجسام، با واحد مکعب طول (میلیمتر مکعب، سانتیمتر مکعب، متر مکعب و غیره) بیان میشود.
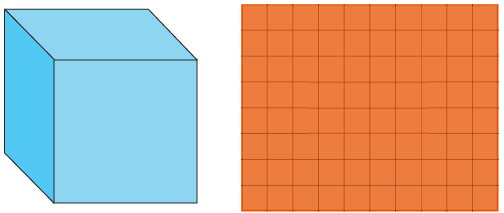
لیوانی پر از آب را بر روی یک میز تصور کنید. میزان آب درون لیوان، برابر با حجم یا ظرفیت لیوان است. سطح تماس لیوان با میز (سطح اشغال شده بر روی میز) نیز به اندازه مساحت کف آن خواهد بود.
محاسبه آنلاین مساحت شکل های هندسی
سایتهای اینترنتی متعددی برای محاسبه مساحت شکلهای دوبعدی و سهبعدی وجود دارند. این سایتها، امکان محاسبه سریع مساحت و مساحت رویه را به سادهترین و قابل فهمترین شکل ممکن فراهم میکنند. از بهترین ابزارهای اینترنتی موجود برای تعیین آنلاین مساحت شکلهای هندسی میتوان به سایت Calculator.net و OmniCalculator اشاره کرد.
- ابزار محاسبه مساحت شکلهای دوبعدی در Calculator.net (+)
- ابزار محاسبه مساحت شکلهای دوبعدی در OmniCalculator (+)
- ابزار محاسبه مساحت شکلهای سهبعدی در Calculator.net (+)
- ابزار محاسبه مساحت شکلهای سهبعدی در OmniCalculator (+)
هر کدام از ابزارهای بالا، از قابلیتهای مختص به خود بهره میبرند. تصویر زیر، ابزار محاسبه مساحت شکلهای دوبعدی در OmniCalculator را نمایش میدهد.
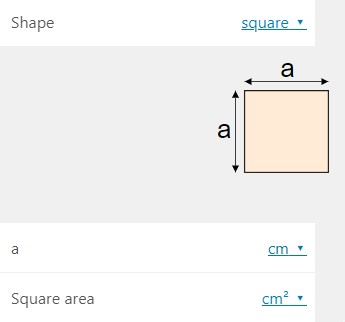
در منوی بازشونده مقابل عنوان «Shape»، امکان انتخاب شکل مورد نظر فراهم شده است. به عنوان مثال، در تصویر بالا، این منو بر روی گزینه «square» قرار دارد. بنابراین، پارامترهای مورد نیاز برای محاسبه مساحت مربع در کادر ماشینحساب نمایش داد میشود. با کلیک بر روی منو، میتوان شکلهای دیگر را نیز انتخاب کرد.
در اینجا، قصد داریم مساحت یک مثلث را با استفاده از اندازههای ارتفاع و قاعده آن به دست بیاوریم. به این منظور، بر روی گزینه «triangle» کلیک میکنیم. با این کار، پارامترهای مورد استفاده برای تعیین مساحت (base and height)، شکل مثلث و کادرهای مربوط به وارد کردن اندازه پارامترها به نمایش درمیآیند.
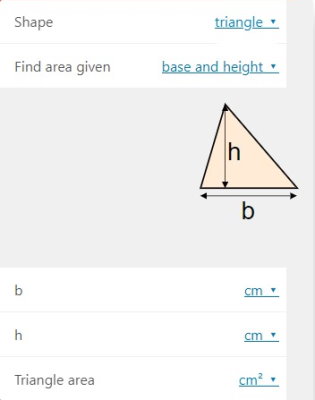
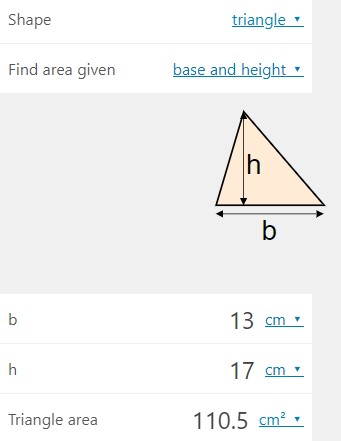
اگر اندازه قاعده و ارتفاع مثلث مورد نظر ما برابر با ۱۳ و ۱۷ سانتیمتر باشد، عدد ۱۳ را در مقابل کارد «b» و عدد ۱۷ را در مقابل کادر «h» وارد میکنیم. با این کار، اندازه مساحت در کادر «Triangle area» به نمایش درمیآید.
اندازه گیری مساحت توسط ابزارهای تخصصی
مساحت، یکی از اندازههای مهمی است که در حوزههای مختلف طراحی، مهندسی، نقشهبرداری، اطلاعات جغرافیایی و غیره مورد استفاده قرار میگیرد. ابزارهای تخصصی این حوزهها، معمولا امکان اندازهگیری مساحت را برای کاربران فراهم میکنند. در این بخش قصد داریم نحوه تعیین مساحت در گوگل مپ (بزرگترین پلتفرم نقشهبرداری دنیا) و اتوکد (محبوبترین نرمافزار طراحی مهندسی) را آموزش دهیم.
روش اندازه گیری مساحت در گوگل مپ چیست ؟
«گوگل مپ» (Google Map)، محبوبترین سرویس اینترنتی مشاهده نقشهها و تصاویر ماهوارهای از سطح زمین است. تصویر زیر، نقشه گوگل مپ از ساختمانهای موجود در یک محدوده را نمایش میدهد. قصد داریم مساحت ساختمان نمایش داده شده را به دست بیاوریم.
به منظور تعیین مساحت ساختمان، ابتدا بر روی یکی از گوشههای آن کلیک راست کرده و گزینه «Measure distance» را انتخاب میکنیم.

به این ترتیب، نقطهای بر روی محل کلیک راست ظاهر میشود. با گرفتن این نقطه توسط کلیک چپ و حرکت دادن نشانگر ماوس میتوان محل این نقطه را تنظیم کرد.

در مرحله بعد، گوشههای بعدی ساختمان را نیز علامتگذاری میکنیم.

پس از علامتگذاری گوشه آخر، بر روی گوشه اول کلیک میکنیم تا محدوده مورد نظر بسته شود. با این کار، ضمن بسته شدن محدوده، مساحت آن در کادر پایین صفحه و در مقابل عنوان «Total area» ظاهر میشود.

روش اندازه گیری مساحت در اتوکد چیست ؟
اتوکد، یکی از پرکاربردترین نرمافزارهای طراحی مهندسی است. دستورات مختلفی برای محاسبه مساحت المانهای ترسیمی در این نرمافزار وجود دارند. این دستورات عبارت هستند از:
- AREA
- MEASUREGEOM
- MASSPROP
- BOUNDARY
- LIST
با کلیک بر روی یک المان دوبعدی بسته و اجرای دستورات بالا، اندازه مساحت المان انتخابی به نمایش در میآید. به منظور آشنایی بیشتر با نحوه محاسبه مساحت و اندازهگیری آن در اتوکد، مطالعه مطالب زیر از مجله فرادرس را به شما پیشنهاد میکنیم:
- محاسبه مساحت در اتوکد — کاملترین آموزش تصویری و رایگان + همه روشها
- اندازهگذاری در اتوکد — آموزش از صفر تا صد + مثال
سوالات متداول در رابطه با مساحت
در این بخش، به برخی از سوالات پرتکرار در رابطه با مساحت به طور خلاصه پاسخ میدهیم.
مساحت یعنی چه ؟
مساحت، اندازه محدوده درون شکلهای دوبعدی و رویه بیرونی شکلهای سهبعدی است.
مساحت چه نوع کمیتی است ؟
مساحت، یک نوع کمیت اسکالر (عددی) است.
مساحت ایران چقدر است ؟
مساحت ایران برابر با ۱۶۴۸۱۹۵ کیلومتر مربع است.
یکای مساحت در ایران چیست ؟
در ایران، مساحت با یکای متر مربع و دیگر یکاهای SI بیان میشود.
تفاوت مساحت با محیط و حجم چیست ؟
مساحت یک کمیت دوبعدی است؛ در حالیکه محیط، یک کمیت تکبعدی و حجم، یک کمیت سهبعدی است.
روش به دست آوردن مساحت شکل های نامنظم چیست ؟
مساحت شکلهای نامنظم با استفاده از تقسیمبندی آنها به شکلهای کوچک (مانند مثلثبندی) و روشهای تخمینی (مانند نقطه میانی، آفست، سیمپسون و غیره) به دست میآید.













با سلام، در جدول فرمول مساحت ها در قسمت استوانه h جا افتاده در تایپ و در قسمت نیم کرده هم فرمول کره دوباره تکرار شده که فک کنم اگر مساحت کلی نیم کره مد نظرتون بود باید 3 پی r به توان 2 میبایست نوشته میشد. بعدا هم در قسمت توضیحات همین مشکلات تکرار شده. با تشکر از مطلب ارزشمندتون.
با سلام و وقت بخیر؛
اشکلات اصلاح شدند. ممنون از دقت نظر شما.
از همراهیتان با مجله فرادرس سپاسگزاریم.