مساحت مربع با قطر چگونه بدست می آید؟ – به زبان ساده + حل تمرین و مثال

مساحت مربع با قطر از رابطه «اندازه قطر در خودش تقسیم بر دو» یا ۲ ÷ (d×d) =A به دست می‌آید. قطر مربع، پاره‌خطی است که گوشه‌های روبه‌رویی آن را به هم وصل می‌کند. در این آموزش از مجله فرادرس، به معرفی فرمول‌ها و نحوه محاسبه مساحت مربع با قطر همراه با حل چندین مثال متنوع و کاربردی می‌پردازیم.

مساحت مربع چیست و چگونه بدست می آید؟

به سطح محدود به ضلع‌های مربع، مساحت می‌گویند. مساحت مربع از ضرب اندازه یک ضلع در خودش به دست می‌آید.

البته در صورت مشخص بودن اندازه قطر مربع نیز می‌توان مساحت آن را تعیین کرد.

قطر مربع چیست؟

قطر مربع، فاصله بین دو گوشه مقابل در مربع است. در شکل‌های چندضلعی، قطر به عنوان پاره‌خط اتصال‌دهنده دو راس غیر مجاور در نظر گرفته می‌شود.

محاسبه مساحت مربع با قطر چگونه است؟

فرمول مساحت مربع با قطر برابر است با:

۲ ÷ (قطر × قطر) = مساحت مربع

عبارت جبری مساحت مربع با قطر به صورت زیر نوشته می‌شود:

$$
A= \frac {۱} {۲} d \times d
$$

یا

$$
A= \frac {۱} {۲} d^۲
$$

• A: مساحت مربع
• d: قطر مربع

مثال 1: محاسبه مساحت مربع با قطر

مساحت مربعی با قطر 7 را حساب کنید.

بر اساس رابطه مساحت مربع داریم:

۲ ÷ (قطر × قطر) = مساحت مربع

۲ ÷ (۷ × ۷) = مساحت مربع

۲ ÷ (۴۹) = مساحت مربع

۲۴/۵ = مساحت مربع

در نتیجه مساحت مربع برابر ۲۴/۵ واحد سطح است. واحد سطح معمولا به صورت میلی‌متر مربع، سانتی‌متر مربع، متر مربع، اینچ مربع و غیره بیان می‌شود.

مثال 2: محاسبه مساحت مربع به صورت جبری

مساحت مربع زیر را به دست بیاورید.

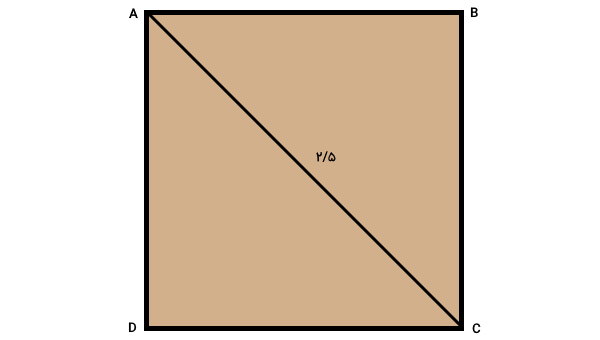
پاره‌خطی که گوشه A را به گوشه C وصل کرده (پاره‌خط AC)، قطر مربع نام دارد. اندازه این پاره‌خط برابر 2/5 است. بر اساس فرمول مساحت مربع با قطر داریم:

$$
A= \frac {۱} {۲} d \times d
$$

• A: مساحت مربع
• d: قطر مربع برابر 2/5

اندازه قطر را درون فرمول بالا قرار داده و محاسبات آن را انجام می‌دهیم:

$$
A= \frac {۱} {۲} \times ۲/۵ \times ۲/۵
$$

$$
A= \frac {۱} {۲} \times ۶/۲۵
$$

$$
A= ۳/۱۲۵
$$

در نتیجه، مساحت مربع برابر ۳/۱۲۵ واحد سطح است.

مثال 3: محاسبه مساحت مربع به روش توانی

قطر مربعی برابر ۸ سانتی‌متر است. مساحت مربع را با فرمول توانی تعیین کنید.

فرمول توانی مساحت مربع به صورت زیر نوشته می‌شود:

$$
A= \frac {۱} {۲} d^۲
$$

• A: مساحت مربع
• d: قطر مربع برابر ۸ سانتی‌متر

هنگامی که یک عدد در خودش ضرب می‌شود، شکل ریاضی آن را با توان نمایش می‌دهند. به عنوان مثال، مساحت مربع از ضرب اندازه یک ضلع در خودش به دست می‌آید. به عبارت دیگر، مساحت مربع، توان دو یک ضلع آن است. در فرمول با نیز از توان دو قطر استفاده شده است. در واقع، تفاوت زیادی در نحوه حل این مثال با مثال‌های قبل وجود ندارد. بنابراین، داریم:

$$
A= \frac {۱} {۲}\times ۸^۲
$$

توان دو عدد ۸ برابر ۶۴ است:

$$
A= \frac {۱} {۲}\times ۶۴
$$

$$
A= ۳۲
$$

در نتیجه، مساحت مربع برابر ۳۲ سانتی‌متر مربع خواهد بود.

اثبات فرمول مساحت مربع با قطر

مساحت مربع با قطر، بازنویسی فرمول مساحت مربع با ضلع است. این فرمول، به کمک قضیه فیثاغورس نوشته می‌شود.

مربع زیر را در نظر بگیرید. اگر قطر این مربع را رسم کنیم، دو مثلث به وجود می‌آید.

مطابق با خواص مربع، زاویه تمام راس‌های این چهارضلعی برابر ۹۰ درجه است. بنابراین، دو مثلث بالا، قائم الزاویه هستند. قطر مربع، وتر این دو مثلث و ضلع‌های آن، ساق‌های این دو مثلث محسوب می‌شوند.

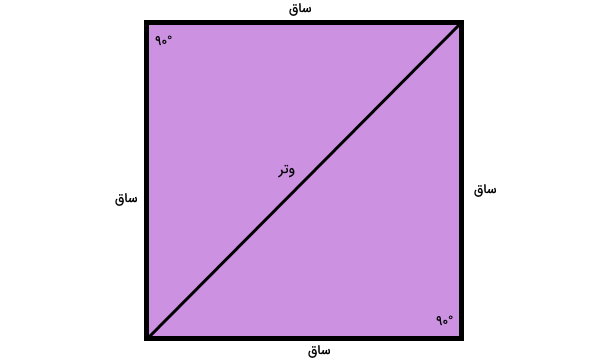
بر اساس قضیه فیثاغورس داریم:

توان دو ساق دوم + توان دو ساق اول = توان دو وتر

به عبارت دیگر:

توان دو ضلع مربع + توان دو ضلع مربع = توان دو قطر مربع

شکل ریاضی رابطه بالا به صورت زیر نوشته می‌شود:

$$
d^۲ = a^۲ + a^۲
$$

$$
d^۲ = ۲a^۲
$$

اکنون رابطه بالا را بر حسب اندازه ضلع (a) بازنویسی می‌کنیم:

$$
a^۲ = \frac {d^۲} {۲}
$$

$$
a = \sqrt {\frac {d^۲} {۲}}
$$

$$
a = \frac {d} {\sqrt {{۲}}}
$$

رابطه بالا را به خاطر داشته باشید. فرمول مساحت مربع با ضلع برابر است با:

$$
A = a^۲
$$

رابطه بین ضلع (a) و (d) را درون این فرمول قرار می‌دهیم:

$$
A = (\frac {d} {\sqrt {{۲}}})^۲
$$

$$
A = \frac {d^۲} {(\sqrt {{۲}})^۲}
$$

$$
A = \frac {d^۲} {۲}
$$

فرمول بالا، همان فرمول مساحت مربع با قطر است.

حل مثال های مساحت مربع با قطر

در این بخش، به حل چند مثال بیشتر می‌پردازیم.

مثال ۴: محاسبه مساحت مثلث متساوی الساقین قائم الزاویه

تصویر زیر، یک مثلث متساوی الساقین قائم الزاویه را نمایش می‌دهد. در این نوع مثلث، اندازه ساق‌ها با هم برابر هستند. با توجه به اندازه وتر مثلث، فرمول مساحت آن را به دست بیاورید.

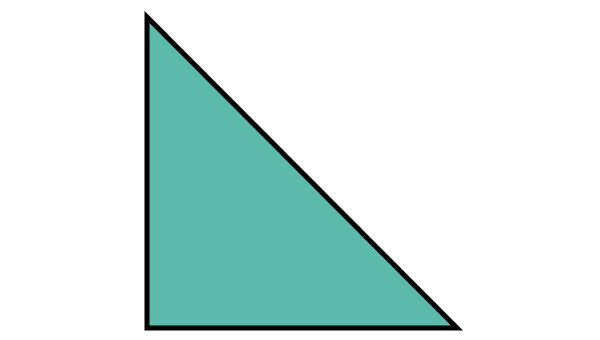
به منظور محاسبه مساحت مثلث بالا، یک مثلث هم‌نهشت با آن را در نظر بگیرید. وتر این مثلث را بر روی وتر مثلث اول منطبق می‌کنیم.

از آنجایی که تمام ضلع‌های دو مثلث با هم برابر هستند، با قرار دادن آن‌ها در کنار یکدیگر، یک مربع ایجاد می‌شود. بنابراین، می‌توانیم بگوییم:

دو مثلث متساوی الساقین قائم الزاویه = مربع

یا به عبارت دیگر:

نصف مربع = مثلث متساوی الساقین قائم الزاویه

وتر مثلث‌ها، همان قطر مربع است. مساحت مربع از فرمول زیر به دست می‌آید:

$$
A= \frac {۱} {۲} d^۲
$$

در نتیجه، فرمول مساحت مثلث متساوی الساقین قائم الزاویه برابر است با:

$$
A = \frac {۱} {۲} \times \frac {d^۲} {۲}
$$

$$
A = \frac {d^۲} {۴}
$$

رابطه بالا، با عنوان فرمول مساحت مثلث قائم الزاویه متساوی الساقین با وتر شناخته می‌شود.

مثال ۵: محاسبه مساحت مربع محاطی

چندضلعی محاطی، شکلی است که تمام راس‌های آن بر روی محیط دایره قرار می‌گیرد. تصویر زیر، یک مربع محاطی را نمایش می‌دهد. اگر شعاع دایره برابر 15 متر باشد، مساحت مربع محاطی چقدر است؟

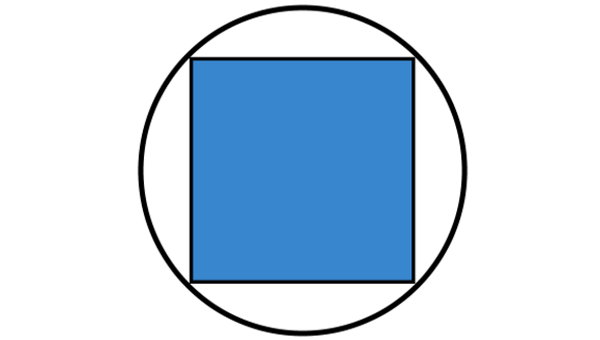
قطر مربع محاطی، با قطر دایره محیط بر آن برابر است. از طرفی، شعاع دایره، اندازه قطر دایره دو برابر شعاع آن است. بنابراین، قطر مربع برابر دو برابر شعاع دایره یا 30=15×2 خواهد بود.

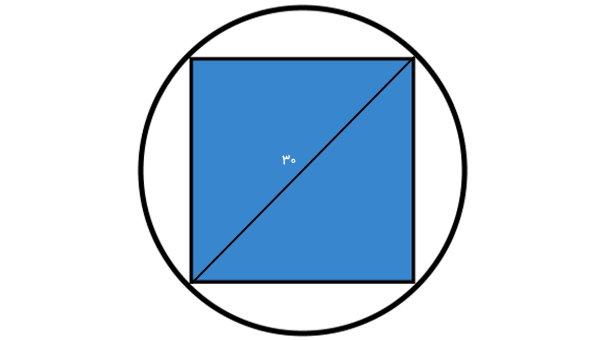
قطر دایره محیطی را درون فرمول مساحت مربع با قطر قرار می‌دهیم:

$$
A= \frac {۱} {۲} d^۲
$$

$$
A= \frac {۱} {۲} \times ۳۰^۲
$$

$$
A= \frac {۱} {۲} \times ۹۰۰
$$

$$
A= ۴۵۰
$$

در نتیجه، مساحت مربع داخل دایره برابر 450 متر مربع است.

سوالات متداول در رابطه با مساحت مربع با قطر

در این بخش، به برخی از سوالات متداول در رابطه با مساحت مربع با قطر به طور خلاصه پاسخ می‌دهیم.

آیا امکان محاسبه مساحت مربع فقط با قطر وجود دارد؟

بله. اگر فقط اندازه قطر مربع را داشته باشیم، می‌توانیم مساحت آن را به دست بیاوریم.

مساحت مربع با قطر چگونه محاسبه می‌شود؟

مساحت مربع با «ضرب اندازه قطر در خودش تقسیم بر دو» محاسبه می‌شود.

مساحت مربع با قطر به صورت جبری چیست؟

فرمول ۲÷ (d×d)=A، مساحت مربع به زبان ریاضی یا به صورت جبری است.

فرمول مساحت مربع با قطر چگونه بدست می‌آید؟

فرمول مساحت مربع با قطر با استفاده از قضیه فیثاغورس در مثلث‌های قائم الزاویه اثبات می‌شود.