عدد پی (Π) چیست؟ — کاربردها به زبان ساده

عدد پی یکی از اعداد جالب و رمزآلود است که احتمالاً نام آن را از ریاضیات دوران مدرسه به یاد دارید و با شنیدن آن عدد ۳٫۱۴ در ذهنتان متبادر می‌شود. در این مطلب از مجله فرادرس عدد پی را با بیان تاریخچه مختصری از آن معرفی می‌کنیم، روش‌های تقریب این عدد را ارائه می‌کنیم و درباره کاربردهایش بحث خواهیم کرد.

عدد پی چیست؟

«عدد پی» (Pi Number) یک ثابت ریاضی است که نسبت محیط دایره به قطر آن را نشان می‌دهد. مقدار تقریبی عدد پی برابر با ۳٫۱۴ است که معمولاً برای کسانی که با ریاضیات سر و کار دارند، عدد آشنایی است. از اواسط قرن هجدهم میلادی عدد پی با حرف یونانی $$\pi$$ نمایش داده می‌شود، اگرچه گاهی اوقات آن را به صورت pi نیز می‌نویسند. پی یک عدد گنگ است، به این معنی که نمی‌توان آن را به شکل نسبت دو عدد صحیح بیان کرد (کسرهایی مانند ۲۲/۷ یا امثال آن، معمولاً برای تقریب $$\pi$$ به کار می‌روند).

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

در قالب یک تعریف ریاضی رسمی، $$\pi$$ برابر با نسبت محیط دایره ($$C$$) به قطر آن ($$d$$) تعریف می‌شود. از این رو، تساوی $$\pi = C/d$$ برقرار است. نسبت $$C$$ به $$d$$ همیشه بدون در نظر گرفتن اندازه دایره، $$\pi$$ به یک است.

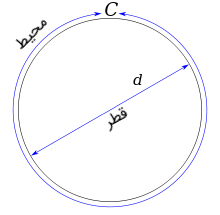
نمادی که ریاضی‌دانان برای نشان دادن نسبت دور یک دایره به قطر آن استفاده می‌کنند، حرف یونانی $$\pi$$ است. این حرف (و بنابراین خود عدد پی) را می‌توان با کلمه لاتین pi نشان داد. در انگلیسی، $$\pi$$ به صورت «پای» تلفظ می‌شود. حروف کوچک $$\pi$$ را نباید با حرف بزرگ $$\Pi$$ اشتباه گرفت، که نماد ضرب دنباله‌ها است.

تاریخچه عدد پی

اولین تقریب‌های مکتوب مربوط به عدد پی از مصر باستان و بابل گرفته شده است و نزدیک به ۴۰۰۰ سال قدمت دارد. به عنوان مثال، یک لوح سفالین بابل از حدود ۱۹۰۰ سال قبل از میلاد، عدد ۳٫۱۲۵ را نشان داده، در حالی که «پاپیروس ریاضی ریند» (Rhind Mathematical Papyrus) در مصر از ۱۶۵۰ سال قبل از میلاد این مقدار را ۳٫۱۶۰۵ مشخص کرده است.

فیلم آموزش خلاقیت و هوش مالی کودکان و نوجوانان در فرادرس

کلیک کنید

بعدها در حدود ۲۵۰ سال قبل از میلاد، ریاضی‌دان بزرگ یونان باستان، ارشمیدس، با استفاده از الگوریتم (یا مجموعه‌ای از قوانین مشخص) یک رویکرد جدید هندسی را برای تقریب عدد پی در طیف معینی از اعداد معرفی کرد و دریافت که می‌توان از این عدد ثابت برای محاسبه مساحت سطح و حجم یک کره استفاده کرد.

در حدود سال ۴۸۰ میلادی، ریاضی‌دان برجسته چینی «تسو چونگچی» (Zu Chongzhi) - که با روش ارشمیدس آشنا نبود - موفق شد با استفاده از یک رویکرد مبتنی بر الگوریتم، تقریب ۳٫۱۴۱۵۹۲۹۲۰ را برای عدد پی محاسبه کند. این رقم دقیق‌ترین تخمین تا ۸۰۰ سال بعد بود.

سپس، در قرن شانزدهم و هفدهم، تکنیک‌های سری نامتناهی در محاسبه پی متحول شدند و این امکان را دادند که تعداد اعشار به طور دقیق‌تر به دست آید. در سال 1706، «ویلیام جونز» (William Jones)، آموزگار ریاضی بریتانیایی، در کتاب "A New Introduction to the Mathematics" از یک حرف یونانی برای نشان دادن عدد پی استفاده کرد. قبل از آن، به طور معمول از تقریب‌های کسری مانند ۲۲/۷ و ۳۵۵/۱۱۳ برای بیان این عدد استفاده می‌شد.

جالب است بدانید که در ایران نیز در قرن نهم هجری، غیاث‌الدین جمشید کاشانی، ریاضی‌دان ایرانی، در «رسالة المحیطیه» که عدد پی را تا ۱۶ رقم اعشار درست اراسه کرد و تا ۱۸۰ سال بعد کسی نتوانست تقریب بهتری معرفی کند.

در سال‌های اخیر، ظهور رایانه‌ها این امکان را فراهم کرده است که عدد پی با دقتی نجومی و بسیار زیاد محاسبه شود، چیزی فراتر از آنچه آرشیمیدس و امثال او می‌توانستند تصور کنند.

تقریب عدد پی

در این بخش، روش‌هایی را بیان می‌کنیم که با استفاده از آن‌ها عدد پی تقریب زده می‌شود و تعریف می‌گردد.

فیلم آموزش هندسه پایه دهم – هندسه ۱ در فرادرس

کلیک کنید

تقریب عدد پی با چند ضلعی ها

با اندازه‌گیری محیط چندضلعی‌ها می‌توان محیط دایره را تقریب زد.

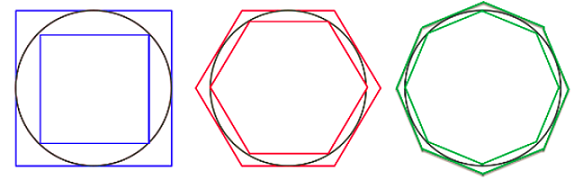
محیط $$n$$ضلعی‌ها را می‌توان از هندسه معمولی مربوط به چند‌ضلعی‌ها به دست آورد و از تقریب زاویه‌ کوچک برای یافتن حد $$2 \pi$$ استفاده کرد.

برای مثال می‌خواهیم تقریب عدد پی را با استفاده از محیط یک مربع محیطی و یک مربع محاطی به دست آوریم.

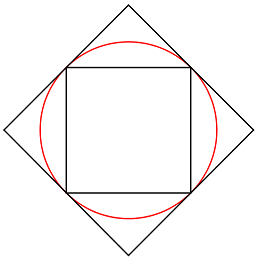
فرض کنید $$P_1$$ محیط مربع بزرگ و $$P_2$$ محیط مربع کوچک و $$C$$ محیط دایره باشد. می‌توان محیط دایره را با میانگین دو محیط تقریب زد:

$$ \large C \approx \frac { P _ 1 + P _ 2 } { 2 } . $$

اگر $$d$$ قطر دایره باشد، اندازه ضلع مربع بزرگ‌تر نیز $$d$$ است. اندازه ضلع مربع کوچک‌تر را می‌توان با استفاده از یک مثلث قائم‌الزاویه یافت. این طول $$\frac{\sqrt{2}}{2}$$ است. اکنون، داریم:

$$ \large \begin {aligned} P _ 1 & = 4 d \\ P _ 2 & = 2 \sqrt { 2 } d . \end {aligned} $$

بنابراین، تقریب محیط دایره $$ C \approx \big ( 2 + \sqrt { 2 } \big ) d $$ است. با تقسیم محیط بر قطر، مقدار تقریبی $$\pi$$ به دست می‌آید:

$$ \large \pi \approx 2 + \sqrt { 2 } . $$

البته این یک تقریب عملاً مناسب نیست. با وجود این، به روش مشابه و با چندضلعی‌های معمولی با ضلع‌های بیشتر، می‌توان تقریب بهتری به دست آورد.

• مطالب پیشنهادی از مجله فرادرس برای مطالعه:
  • نسبت محیط دایره به قطر آن چیست؟ — به زبان ساده
  • نسبت محیط دایره به شعاع آن چیست؟ — به زبان ساده
  • شعاع چیست؟ — شعاع دایره به زبان ساده (+ فیلم آموزش رایگان)
  • محیط دایره با چی متناسب است؟ — به زبان ساده + حل تمرین و مثال

تقریب عدد پی با روش‌های آماری

شبیه‌سازی‌ها و تکنیک‌های آماری بسیاری وجود دارد که می‌توان از آن‌ها برای تقریب $$\pi$$ استفاده کرد. مدت‌ها قبل از اختراع رایانه‌ها، ریاضیدانان فرانسوی «بوفون» (1707-1788) و «لاپلاس» (1749-1827) یک شبیه‌سازی تصادفی را برای تخمین مقدار $$\pi$$ پیشنهاد کردند.

روش «سوزن بوفون» با استفاده از این واقعیت که یک سوزن ممکن است هنگام انداخته شدن روی صفحه هر زاویه‌ای داشته باشد، تقریبی از عدد $$\pi$$ را ارائه می‌دهد.

قضیه: فرض کنید $$n$$ سوزن به طول ۱ روی یک سطح با نوارهای چوبی به عرض ۱ واحد انداخته می‌شوند. مقدار چشم‌داشتی یا همان امید ریاضی تعداد سوزن‌هایی که روی دو نوار چوب می‌افتند و با خط مرز آن‌ها متقاطع هستند، $$\frac {2} {\pi} \cdot n$$ است.

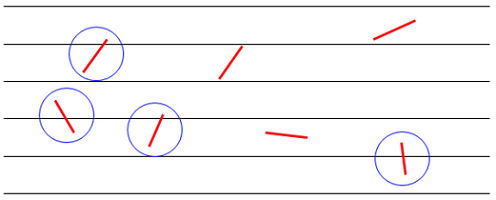
اثبات: اصل اثبات این ایده آن است که هر سوزن را به قسمت‌های کوچک تقسیم کنیم. طبق خاصیت خطی بودن امید ریاضی، تعداد مورد انتظاری که سوزن مرز دو نوار چوب را قطع می‌کند، متناسب با طول سوزن است.

بنابراین، به عنوان تابعی از طول $$l$$، تعداد تقاطع‌های مورد انتظار برای ثابت $$c$$ برابر با $$cl$$ است. در نتیجه، یک دایره با قطر ۱ را در نظر می‌گیریم که محیط آن $$\pi$$ است و با احتمال ۱، این دایره دقیقاً ۲ تقاطع با مرزها خواهد داشت. از این رو، $$c \pi = 2$$ و در نتیجه، $$c=\frac {2} {\pi}$$. برای آشنایی بیشتر با روش سوزن بوفون، پیشنهاد می‌کنیم مطلب «تقریب عدد پی با روش سوزن بوفون — پیاده‌سازی در متلب و پایتون» را در این لینک مطالعه کنید.

این روش، یک تکنیک شبیه‌سازی آسان برای تقریب $$\pi$$ است. به سادگی $$n$$ سوزن را روی زمین پرتاب کنید، تعداد $$x$$ سوزن را که از دو نوار چوب عبور می‌کنند بشمارید و سپس $$ \pi \approx \frac { 2 n } { x } $$. این نوع تکنیک شبیه‌سازی به عنوان شبیه‌سازی مونت کارلو شناخته می‌شود.

تعریف دقیق عدد پی با سری نامتناهی

گرچه $$\pi$$ را نمی‌توان با سری متناهی از اعداد گویا نشان داد (به دلیل گنگ بودن)، اما روش‌های بسیاری برای بیان آن با یک سری بی‌نهایت وجود دارد. از نظر تاریخی، اولین سری برای این تقریب، به صورت زیر است:

$$ \large \frac { 2 } { \pi } = \frac { \sqrt { 2 } } { 2 } \times \frac { \sqrt { 2 + \sqrt { 2 } } } { 2 } \times \frac { \sqrt { 2 + \sqrt { 2 + \sqrt { 2 } } } } { 2 } \times \cdots $$

که در آن، از آنجا که جمله $$n$$اُم ضرب نامتناهی با به کار بردن مکرر فرمول نصف زاویه $$ \cos \frac { \pi } { 2 ^ n } $$ است، داریم:

$$ \large \lim _ { n \rightarrow \infty } \frac { 1 } { 2 ^ n \sin \frac { \pi } { 2 ^ { n + 1 } } } = \frac { 2 } { \pi } $$

زیرا وقتی $$n$$ به بینهایت میل می‌کند، $$ \sin \frac { \pi } { 2 ^ { n + 1 } } \approx \frac { \pi }{ 2 ^ { n + 1 } } $$ است.

سری‌های مفیدتر دیگری نیز هستند که به جای ضرب از جمع بهره می‌برند و محاسبه اولین جملات سری نامتناهی تقریب خوبی از $$\pi$$ به نمایش می‌گذارد. ساده‌ترین سری، «سری گرگوری-لایبنیتس» (Gregory-Leibniz Series) است که از سری تیلور $$\arctan x $$ در ۱ استفاده می‌کند:

$$ \large \frac { \pi } { 4 } = 1 - \frac { 1 } { 3 } + \frac { 1 } { 5 } - \frac { 1 } { 7 } + \cdots . $$

با این حال، این سری به آرامی همگرا می‌شود، به این معنی که جملات زیادی برای دستیابی به تقریب خوب $$\pi$$ لازم است. سری‌های بهتر مثل فرمول‌های «شبه میچین» (Machin-like) نیز وجود دارند:

$$ \large \begin {aligned} \frac { \pi } { 4 } & = 4 \arctan \frac { 1 } { 5 } - \arctan \frac { 1 } { 2 3 9 } \\ \frac { \pi } { 4 } & = 2 2 \arctan \frac { 2 4 4 7 8 } { 8 7 3 1 21 } + 1 7 \arctan \frac { 6 8 5 6 0 1 } { 6 9 0 4 9 9 9 3 } . \end {aligned} $$

در عصر رایانه‌های مدرن، سری‌های حتی بهتری نیز برای تقریب عدد پی شناخته شده‌اند. مانندِ

$$ \large \frac { 1 } { \pi } = \frac { 2 \sqrt { 2 } } { 98 0 1 } \sum _ { k = 0 } ^ { \infty } \frac { ( 4 k ) ! ( 1 1 0 3 + 2 6 3 9 0 k) } { k ! ^ 4 ( 3 9 6 ^ { 4 k } ) } $$

که با استفاده از آن می‌توان عدد پی را تا میلیون‌ها رقم اعشار تقریب زد.

تعریف دقیق عدد پی با انتگرال

عدد $$\pi$$ را با انتگرال نیز می‌توان تعریف کرد. ساده‌ترین مورد، نمایش محیط یا مساحت دایره است:

$$ \large \int _ { - 1 } ^ 1 \sqrt { 1 - x ^ 2 } d x = \frac { \pi }{ 2 } $$

که $$ \left ( x , \sqrt { 1 - x ^ 2 } \right ) $$ نیمه بالایی دایره در بازه $$[-1,1]$$ است.

انتگرال‌های پیچیده‌تری از آمار نیز آمده‌اند، مانند مساحت زیر توزیع نرمال:

$$ \large \int _ { - \infty } ^ { \infty } e ^ { - x ^ 2 } d x = \sqrt { \pi } $$

و توزیع کوشی:

$$ \large \int _ { - \infty } ^ { \infty } \frac { 1 } {x ^ 2 + 1 } d x = \pi . $$

عدد $$\pi$$ در عبارات مختلفی که شامل تابع گاما است نیز ظاهر می‌شود:

$$ \large \Gamma ( t ) = \int _ 0 ^ { \infty } x ^ { t - 1 } e ^ { - x } d x $$

که وقتی مقدار آن را در $$\frac12$$ به دست آوریم، خواهیم داشت:

$$ \large \Gamma \left ( \frac { 1 } { 2 } \right ) = \sqrt { \pi } , ~ ~ \Gamma \left ( \frac { 5 } { 2} \right ) = \frac { 3 } { 4 } \sqrt { \pi } . $$

تقریب عدد پی تا ۵۰۰ رقم اعشار به صورت زیر است:

$$ \begin{align*}\small 3. &141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825\\ \small &3421170679 82148086513282306647093844609550582231725359408128481117450284102701938521105559\\ \small &64462294895493038196 4428810975665933446128475648233786783165271201909145648566923460348610\\ \small &454326648213393607260249141273 724587006606315588174881520920962829254091715364367892590360\\ \small &0113305305488204665213841469519415116094 33057270365759591953092186117381932611793105118548\\ \small & 07446237996274956735188575272489122793818301194912... \end {align*}$$

کاربردهای عدد پی

عدد پی در زندگی واقعی در زمینه‌های مختلفی از قبیل هندسه، علوم، مثلثات، طبیعت و غیره کاربرد دارد.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

عدد پی به طور مشخص در فرمول‌های شاخه‌های علوم از جمله آمار، فراکتال‌ها، ترمودینامیک، مکانیک، کیهان‌شناسی، نظریه اعداد و الکترومغناطیس است. همچنین برای اندازه‌گیری سرعت و قدرت رایانه از آن استفاده می‌شود. بدین ترتیب که از رایانه برای تقریب آن استفاده می‌کنند و وجود هرگونه مشکلی در نرم‌افزار یا سخت‌افزار کشف خواهد شد.

عدد پی در مثلثات برای به دست آوردن مقدار توابع مثلثاتی مانند سینوس، کسینوس، تانژانت و غیره استفاده می‌شود. با این توابع می‌توان سرعت اجسام دوار مانند چرخ کامیون، شفت‌های موتور، قطعات موتور، چرخ‌دنده‌ها و... را اندازه‌گیری کرد. همچنین با کمک عدد پی ولتاژ AC در یک سیم‌پیچ و یک خازن قابل اندازه‌گیری و محاسبه است.

با استفاده از عدد پی می‌توان مواردی مانند موج اقیانوس، امواج نور، امواج صوتی، توزیع ذرات رادیواکتیو و احتمالاتی مانند توزیع سکه‌ها و.. را با استفاده از یک دنباله از دایره‌ها اندازه‌گیری کرد.

چند نمونه از کاربردهای متداول عدد پی به ضرح زیر است:

• در مهندسی برق برای حل مسئله‌های مختلف از $$\pi$$ استفاده می‌شود.
• در آمار از عدد پی برای ردیابی دینامیک جمعیت استفاده می‌شود.
• در علم پزشکی، هنگام مطالعه ساختار چشم عدد پی مورد استفاده قرار می‌گیرد.
• در بیوشیمی و برای درک ساختار و عملکرد DNA عدد پی کاربرد دارد.
• فیزیکدانانی که رفتار موج‌های سیال را بررسی می‌کنند، در محاسبات خود از عدد پی بهره می‌برند.
• طراحان ساعت هنگام طراحی آونگ‌های ساعت‌ها از عدد پی استفاده می‌برند.
• طراحان هواپیما عدد پی را برای محاسبه مساحت پوسته هواپیما به کار می‌برند.
• در پردازش سیگنال و تحلیل طیف (پیدا کردن فرکانس موجی که استفاده می‌کنیم) از عدد پی استفاده می‌شود، زیرا تناوب پایه موج سینوسی $$2 \pi $$ است.
• در ناوبری، مانند موقعیت‌یابی جهانی (GPS) از عدد پی استفاده می‌شود.
• در حل مسائل ریاضیات در هندسه مانند پیدا کردن مساحت دایره و غیره، عدد پی به کار می‌رود.

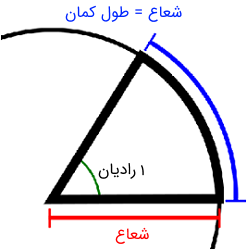
عدد $$\pi$$ در مثلثات مهم است، زیرا تفسیر طبیعی‌تری از زاویه‌ها ارائه می‌دهد (نسبت به درجه‌ها). به طور خاص، رادیان به گونه‌ای تعریف شده است که $$2\pi $$ رادیان معادل یک دایره کامل است (به عبارت دیگر، $$\pi$$، که به عنوان $$\pi$$ رادیان درک می‌شود، معمولاً برابر با ۱۸۰ درجه است که در مثلثات استفاده می‌شود). به این ترتیب، زاویه $$\theta$$ با طول کمان $$\theta \cdot r $$ متناظر است که در آن، $$r$$ شعاع دایره است. به طور معادل، رادیان به گونه‌ای تعریف می‌شود که یک رادیان متناظر با طول قوس برابر با شعاع دایره است.

با استفاده از عدد پی می‌توان اعداد مختلط را در مختصات قطبی بیان کرد، به این معنی که هر عدد مختلط را می‌توان به شکل $$re^{i\theta}$$ برای اعداد حقیقی $$r$$ و $$\theta$$ نوشت. عدد $$\pi$$ در تحلیل اعداد مختلط نقش اساسی دارد، زیرا این عدد مختلط، معادل است با:

$$ \large r e ^ { i \theta } = r ( \cos \theta + i \sin \theta ) $$

همان‌طور که هر دو طرف یک نقطه را در صفحه مختلط نشان می‌دهند. با قراردادن $$\theta = \pi$$ اتحاد معروف زیر حاصل می‌شود:

$$ \large e ^ { i \pi } + 1 = 0 . $$

• مطالب پیشنهادی از مجله فرادرس برای مطالعه:
  • فرمول محیط دایره چیست؟ + حل تمرین و مثال
  • فرمول مساحت دایره چیست؟ — به زبان ساده + حل تمرین و مثال

روز پی

«روز پی» (Pi Day) یک جشن سالانه برای عدد پی است. این روز هر ساله در 14 مارس (۳/۱۴ در قالب روز/ماه میلادی) گرامی داشته می‌شود، زیرا ۳، ۱ و ۴ سه رقم نخست و مهم $$\pi$$ هستند. در سال ۲۰۰۹، مجلس نمایندگان ایالات متحده از تعیین «روز پی» حمایت كرد. همچنین، در چهلمین کنفرانس عمومی یونسکو در نوامبر ۲۰۱۹، روز پی به عنوان روز جهانی ریاضیات معرفی شد.

فیلم آموزش هندسه پایه دهم – هندسه ۱ در فرادرس

کلیک کنید

«روز تقریب پی» (Pi Approximation Day) نیز ۲۲ ماه ژوئیه است (۲۲/۷ در قالب ماه/روز میلادی)، زیرا کسر ۲۲/۷ تقریبی از $$\pi$$ است که تا دو رقم اعشار دقت دارد و ارشمیدس آن را معرفی کرده است.

عدد پی در اکسل

اگر در کارتان به انجام محاسبات هندسی مانند محاسبه مساحت فضای اداری جدید نیاز داشته باشید، باید از عدد پی استفاده کنید. اکسل مقدار $$\pi$$ را تا ۱۵ رقم اعشار ذخیره می‌کند. برای وارد کردن عدد پی در اکسل، مراحل زیر را انجام دهید.

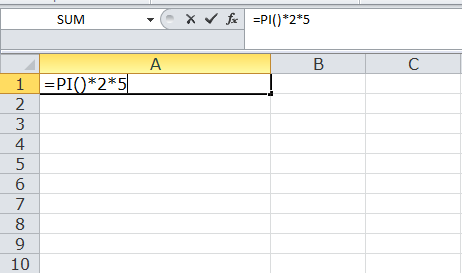
1. اکسل خود را باز کرده و "=" را در یک سلول خالی تایپ کنید تا محتویات آن به عنوان یک فرمول ریاضی برچسب‌گذاری شود.

2. عبارت "PI ()" را تایپ کنید که معادل ۳٫۱۴۱۵۹۲۶۵۳۵۸۹۷۹ در فرمول اکسل است.

3. باقیمانده فرمول خود را تایپ کنید. به عنوان مثال، برای محاسبه محیط یک دایره با شعاع 5 متر، عبارت "۵*۲*" را داخل سلول تایپ کنید.

4. برای اجرای فرمول کلید اینتر را فشار دهید.

عدد پی در متلب

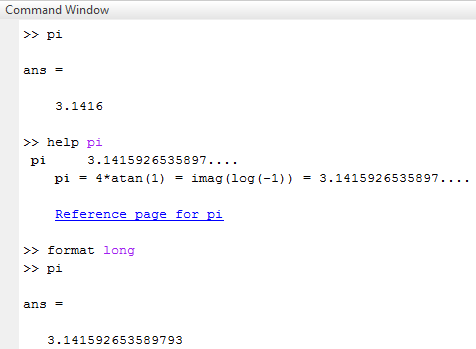
در محاسبات متلب کافی است به جای عدد پی عبارت "pi" را بنویسید. متلب عدد پی را تا ۱۵ رقم اعشار در نظر می‌گیرد. اگر از دستور "format long" استفاده کنید، ۱۵ رقم اعشار نمایش داده می‌شود.

عدد پی در پایتون

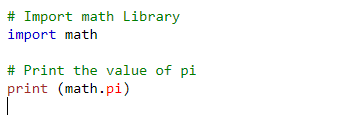
عدد پی در پایتون به صورت "math.pi" تعریف می‌شود. برای مثال، اگر برنامه زیر را بنویسیم، نتیجه آن عدد 3٫141592653589793 خواهد بود.

عدد پی در کیبورد

برای تایپ نماد عدد پی با کیبورد و در یک محیط ادیتور، کافی است ابتدا Num Lock را روشن کنید، سپس با نگه داشتن کلید Alt عدد ۲۲۷ را در قسمت اعداد کیبورد وارد کنید. دقت کنید که با اعداد ردیف بالای حروف در کیبورد نمی‌توانید این کار را انجام دهید.

راز عدد پی

در این بخش، چند مورد جالب را درباره حقایق و رازهای مربوط به عدد پی بیان می‌کنیم.

• علی‌رغم آنچه در تاریخچه عدد پی گفتیم، منشأ دقیق کشف آن هنوز ناشناخته اشت، هرچند آن را به بابلیان یا مصری‌ها نسبت می‌دهند.
• جشن سالانه پی در تاریخ ۳/۱۴ و از ساعت ۱:۵۹ بعد از ظهر آغاز می‌شود. این‌ها در واقع عدد پی را با پنج رقم اعشار می‌سازند: ۳٫۱۴۱۵۹.
• انسان‌ها ۳۵۰۰ سال است که در جست‌وجوی پایان رقم‌های نامحدود عدد پی هستند که هنوز هم با کامپیوتر قابل حل نیست.
• آلبرت انیشتین در روز پی، یعنی ۱۴ مارس ۱۸۷۹ متولد شده است.
• در همه جای جهان عدد پی وجود دارد، حتی در چشمانمان.
• در دادگاه محاکمه «او. جی. سیمپسون» (O. J. Simpson)، قاضی و نماینده FBI سعی کردند با بحث درباره مقدار پی هوشمندی خود را نشان دهند.
• در سال ۲۰۱۰، مهندس سیستم ژاپنی، «شیجرو کوندو» (Shigeru Kondo)، و مهندس کامپیوتر آمریکایی، «الكساندر یی» (Alexander Yee)، ركورد بیشترین رقم‌های محاسبه شده عدد پی را شکستند. آن‌ها این كار را با استفاده رایانه‌های رومیزی، ۲۰ هارد دیسک اکسترنال و نبوغ عجیب و غریب خود انجام دادند و عدد پی را تا پنج تریلیون اعشار تقریب زدند.
• «سورش کومار شرما» (Suresh Kumar Sharma) علاقه‌مند ریاضی اهل هند در حال حاضر رکورد جهانی را برای بیشترین ارقام حفظ شده در اختیار دارد. وی در 17 ساعت و 14 دقیقه، 70 هزار و ۳۰ رقم را گفت.
• رمز مخفی در فیلم «پرده پاره» (Torn Curtain) محصول سال ۱۹۶۶ آلفرد هیچکاک، پی بود.
• رقم‌های بعد از اعشار عدد پی هیچ الگوی منظمی ندارند.