قطر مربع چیست و چگونه بدست می آید؟ – به زبان ساده + حل تمرین و مثال


قطر مربع پارهخطی است که گوشههای روبهرویی مربع را به هم وصل میکند. مربع دو قطر دارد. این قطرها، در محاسبه اندازههای مختلف نظیر ضلع، محیط و مساحت کاربرد دارند. در این آموزش، به معرفی مفهوم، خواص و فرمول قطر مربع به همراه حل چندین مثال متنوع میپردازیم.
مربع چیست؟
مربع، شکلی با چهار ضلع مساوی و چهار گوشه با زاویه قائمه است. به دلیل برابر بودن اندازه ضلعها و زاویههای داخلی، این شکل به عنوان یک چندضلعی منتظم در نظر گرفته میشود.
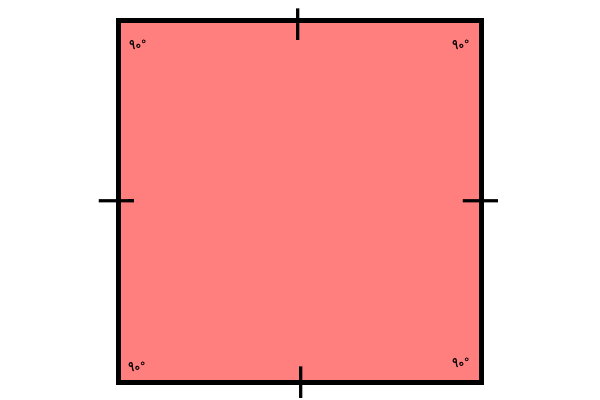
اجزای مربع چه هستند؟
از اجزای اصلی مربع میتوان به ضلع، راس و زاویه داخلی آن اشاره کرد. قطر، یکی از دیگر از اجزای مربع است که در محاسبه اندازههای مختلف نظیر محیط و مساحت مربع مورد استفاده قرار میگیرد.
قطر مربع چیست؟
مربع زیر را در نظر بگیرید. این مربع، از چهار راس یا گوشه تشکیل میشود.

یکی از گوشههای مربع را توسط پارهخط به گوشه مقابل آن وصل میکنیم. این پاره خط، همان قطر مربع است.
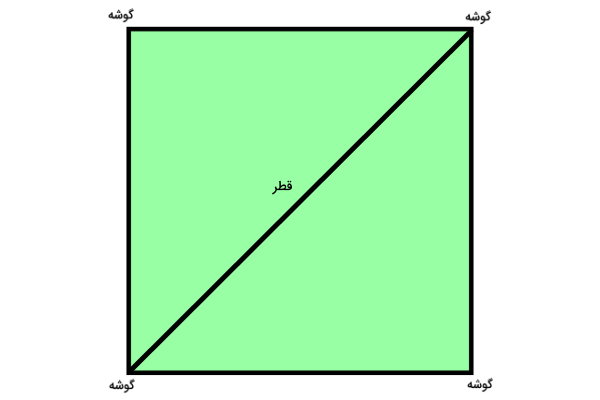
علاوه بر دو گوشه بالا، امکان اتصال دو گوشه دیگر مربع با یک پارهخط نیز وجود دارد.
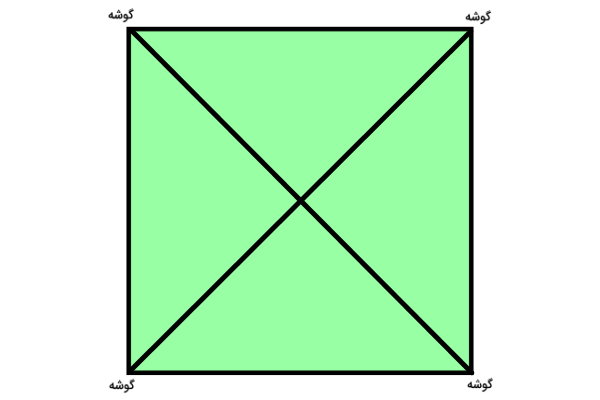
همانطور که مشاهده میکنید، مربع دو قطر دارد. در بخش بعدی، ویژگیها و خواص قطرهای مربع را مورد بررسی قرار میدهیم.
خواص قطر مربع چه هستند؟
قطر مربع دارای ویژگیها و خواص متعددی که در ادامه به معرفی برخی از مهمترین آنها میپردازیم:
- قطرهای مربع یکدیگر را تحت زاویه 90 درجه قطع میکنند.
- اندازه دو قطر مربع برابر است.
- قطرها، مربع را به دو مثلث مساوی تقسیم میکنند.
- اندازه هر قطر مربع از اندازه هر ضلع مربع بزرگتر است.
- قطرهای مربع، زاویه 90 درجه هر گوشه را به دو زاویه 45 درجه تقسیم میکنند (قطرها، نیمساز گوشهها هستند).

قطرهای مربع، آن را به دو مثلث قائم الزاویه متساوی الساقین مساوی تقسیم میکنند. وتر این مثلثهای قائم الزاویه، بر روی قطر و ساقهای آنها، بر روی ضلع مربع منطبق هستند. بر اساس خواص مثلثهای قائم الزاویه، اندازه وتر، همیشه بزرگتر از اندازه هر ساق است. به همین دلیل، قطرهای مربع، همیشه بزرگتر از اضلاع آن خواهند بود.
مثال 1: تعیین اندازه های مربع
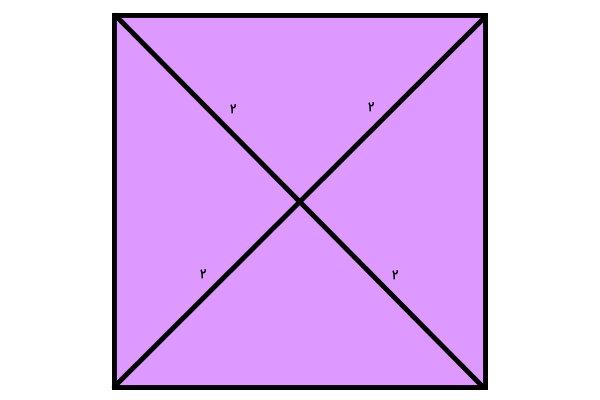
تصویر زیر، یک مربع و قطرهای آن را نمایش میدهد. به جای علامتهای سوال، چه اعدادی را قرار دهیم؟
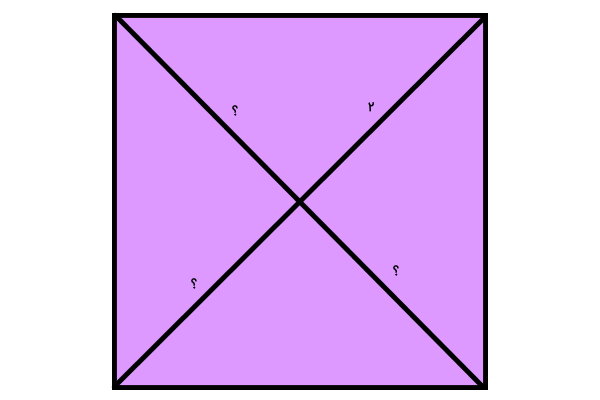
اندازه قسمتی از یک قطر مربع برابر با 2 است. از آنجایی که قطرها یکدیگر را به دو قسمت مساوی تقسیم میکنند، اندازه قسمت دیگر نیز برابر با 2 خواهد بود. دو قطر مربع، اندازه برابر دارند. بنابراین، اندازه بخشهای دیگر نیز 2 خواهد بود.
فرمول اندازه قطر مربع چیست ؟
اندازه قطر مربع برابر با «اندازه یک ضلع ضربدر رادیکال 2» است. فرمول ریاضی محاسبه قطر مربع بر حسب ضلع به صورت زیر نوشته میشود:
- d: قطر مربع
- a: ضلع مربع
مثال 2: محاسبه قطر مربع از روی ضلع
قطر مربعی به ضلع 10 سانتیمتر را حساب کنید. (رادیکال 2 را برابر 1/4 در نظر بگیرید.)
مطابق با فرمول قطر مربع داریم:
- d: قطر مربع
- a: ضلع مربع 10 سانتیمتر
اندازههای معلوم را درون فرمول بالا قرار میدهیم و مطابق با فرض مسئله، به جای رادیکال 2، عدد 1/4 را مینویسیم:
در نتیجه، اندازه قطر مربعی به ضلع 10 سانتیمتر برابر 14 سانتیمتر است.
قطر مربع چگونه بدست می آید ؟
فرمول محاسبه اندازه قطر مربع، بر اساس قضیه فیثاغورس در مثلثهای قائم الزاویه به دست میآید. همانطور که قبلا اشاره کردیم، با رسم یکی از قطرها، مربع به دو مثلث قائم الزاویه تبدیل میشود.
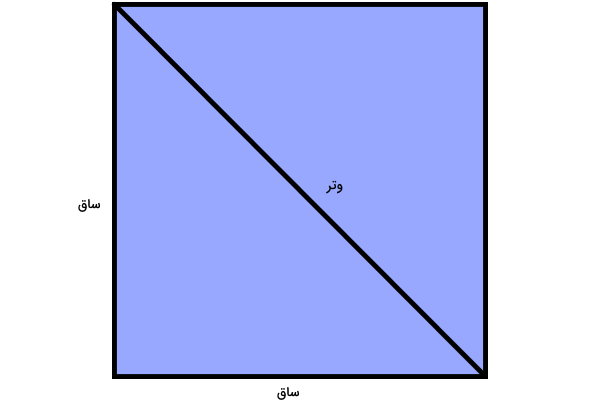
بر اساس قضیه فیثاغورس، وتر و ساقهای مثلث قائم الزاویه دارای رابطه زیر هستند:
- c: وتر
- a: ساق اول
- b: ساق دوم
در مربع، تمام ضلعها با هم برابرند. بنابراین میتوانیم رابطه بالا را به صورت زیر بازنویسی کنیم:
اگر به جای حرف c (وتر مثلث)، حرف d (قطر مربع) را فرار دهیم. رابطه بالا، به همان فرمول محاسبه قطر از روی ضلع مربع تبدیل میشود. علاوه بر این فرمول، امکان محاسبه قطر مربع با استفاده از اندازههای دیگر نظیر مساحت، محیط و غیره نیز وجود دارد. در بخشهای بعدی، به معرفی این فرمولها خواهیم پرداخت.
رابطه بین قطر مربع با مساحت آن
برای نوشتن رابطه مساحت مربع با قطر آن، یک مربع را با رسم قطر به دو مثلث تقسیم میکنیم. قاعده هر مثلث، برابر با اندازه قطر است.

در مرحله بعد، قطر دوم مربع را تا محل برخورد به قطر اول میکشیم. این پاره خط، نصف قطر دوم و ارتفاع نظیر قاعده مثلث است.
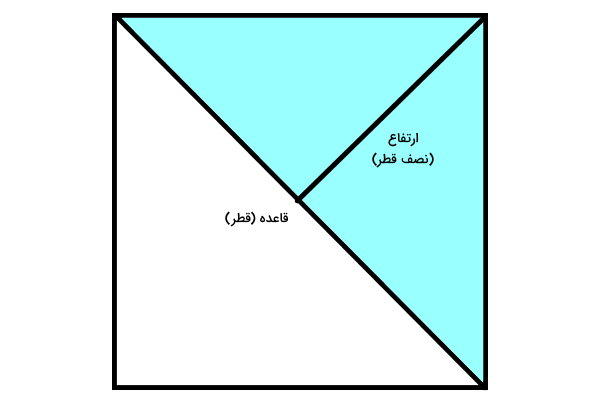
مساحت مثلث از «قاعده در ارتفاع تقسیم بر دو» به دست میآید:
2 ÷ (ارتفاع × قاعده) = مساحت مثلث
به جای قاعده، از عبارت «قطر» و به جای ارتفاع از عبارت «نصف قطر» استفاده میکنیم:
2 ÷ (نصف قطر × قطر) = مساحت مثلث
دو مثلث تشکیلدهنده مربع با هم برابر هستند. مساحت مربع از جمع مساحت این دو مثلث به دست میآید:
مساحت مثلث + مساحت مثلث = مساحت مربع
نصف قطر × قطر = مساحت مربع
2 ÷ (قطر × قطر) = مساحت مربع
عبارت جبری مساحت مربع با قطر، معمولا به صورت زیر نوشته میشود:
- A: مساحت مربع
- d: قطر مربع
مثال 3: محاسبه قطر از روی مساحت آن
مربعی به مساحت 32 متر مربع را در نظر بگیرید. اندازه قطرهای این مربع چند است؟
به منظور محاسبه اندازه قطرهای مربع، فرمول مساحت مربع با قطر را مینویسیم:
2 ÷ (قطر × قطر) = مساحت مربع
- A: مساحت مربع برابر 32 متر مربع
- d: قطر مربع
اندازه مساحت را درون رابطه بالا قرار میدهیم:
در نتیجه، اندازه قطر مربع برابر 8 متر است. فرمول محاسبه مستقیم قطر از روی مساحت به صورت زیر نوشته میشود:
رابطه بین قطر مربع با محیط آن
محیط مربع، از جمع اندازه ضلعهای آن به دست میآید. فرمول محیط مربع به صورت زیر نوشته میشود:
- P: محیط
- a: ضلع
در بخشهای قبلی دیدیم که بین قطر و ضلع مربع، رابطه زیر برقرار است:
- d: قطر
- a: ضلع
اگر رابطه بالا را بر حسب ضلع بنویسیم، خواهیم داشت:
طرف راست این رابطه را درون فرمول محیط قرار میدهیم:
به این ترتیب، اگر اندازه محیط مربع مشخص باشد، امکان تعیین قطر آن فراهم میشود. برای آشنایی با رابطه بین محیط مربع و ضلع آن، مطالعه مطلب «طول ضلع مربع به محیط آن چیست؟ + حل تمرین و مثال» را به شما پیشنهاد میکنیم.
مثال 4: محاسبه قطر از روی محیط
اگر محیط یک مربع برابر 14 میلیمتر باشد، قطر آن چقدر است؟ (رادیکال 2 را برابر 1/4 در نظر بگیرید.)
برای حل این مثال، فرمول محیط مربع بر حسب قطر مینویسیم و اندازههای معلوم را درون آن قرار میدهیم:
- P: محیط برابر 14 میلیمتر
- d: قطر
در نتیجه، اندازه قطر مربع برابر 5 میلیمتر است. فرمول محاسبه مستقیم قطر از روی محیط به صورت زیر نوشته میشود:
رابطه بین قطر مربع و اجزای دایره محیطی و محاطی
دایره محاطی، دایرهای است که داخل یک شکل هندسی قرار میگیرد و به تمام ضلعهای آن شکل مماس میشود. تصویر زیر، نمونهای از دایره محاط در یک مربع را نمایش میدهد.

در دایره محاطی بالا، اندازه قطر دایره با اندازه ضلع مربع برابر است. بنابراین میتوان قطر مربع را با استفاده از اندازه قطر دایره به دست آورد:
- ds: قطر مربع
- dc: قطر دایره محیطی
اگر تمام گوشههای یک شکل هندسی بر روی محیط یک دایره قرار گیرند، به آن دایره، دایره محیطی میگویند. تصویر زیر، یک دایره محیط بر مربع را نمایش میدهد.
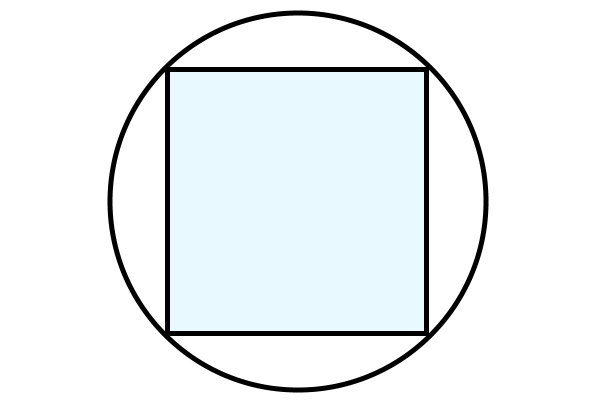
در دایره محیطی، اندازه قطر مربع با اندازه قطر دایره برابر است.
مثال 5: محاسبه ضلع مربع محاطی
قطر یک دایره برابر 21 سانتیمتر است. اندازه ضلع مربع محاط در دایره را حساب کنید. (رادیکال 2 را برابر 1/4 در نظر بگیرید.)
به منظور تعیین اندازه ضلع مربع، به اندازه قطر آن نیاز داریم. از آنجایی که مربع، محاط در دایره است، قطر آن با قطر دایره محیطی برابر (21 سانتیمتر) خواهد بود. رابطه بین قطر و ضلع مربع نیز به صورت زیر نوشته میشود:
- d: قطر برابر 21 سانتیمتر
- a: ضلع
در نتیجه، ضلع مربع برابر 15 سانتیمتر است.
محاسبه آنلاین قطر مربع
از ابزارهای اینترنتی موجود برای محاسبه آنلاین قطر مربع میتوان به موتور جستجوی گوگل (+)، سایت Omni Calculator (+) و سایت Calculator Soup (+) اشاره کرد. از میان این موارد، ماشین حساب سایت Calculator Soup، امکانات بیشتری را در اختیار کاربر قرار میدهد (تصویر زیر).
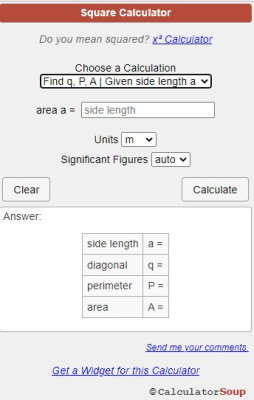
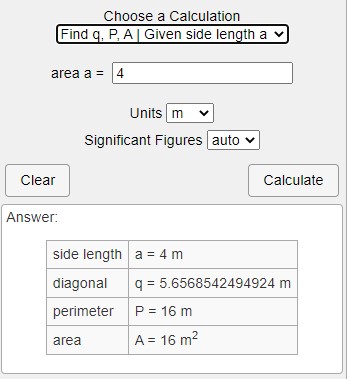
در ماشین حساب اینترنتی بالا، امکان انتخاب اندازههای مربع بر حسب یکی از اندازههای ضلع، قطر، محیط و مساحت فراهم شده است. به عنوان مثال، گزینه پیش فرض (تصویر بالا) را انتخاب کرده و عدد 4 را در کادر خالی وارد میکنیم. با کلیک چپ بر روی گزینه «Calculate»، قطر مربع به همراه محیط و مساحت آن محاسبه میشود. بر اساس خروجی این ماشین حساب، قطر مربع تقریبا برابر 5/66 است.
سوالات متداول در رابطه با قطر مربع
در این بخش، به برخی از سوالات پرتکرار در رابطه با قطرهای مربع به طور خلاصه پاسخ میدهیم.
تعریف قطر مربع چیست ؟
قطر مربع، پاره خطی است که دو راس مقابل را به هم وصل میکند.
مربع چند قطر دارد؟
مربع، دو قطر با اندازههای برابر دارد.
قطرهای مربع چه رابطهای با هم دارند؟
قطرهای مربع، عمود منصف یکدیگرند.
نسبت قطرهای مربع چند است؟
قطرهای مربع با یکدیگر برابر هستند. به عبارت دیگر، نسبت این قطرها برابر 1 است.
آیا قطر مربع با اضلاعش برابر است؟
خیر؛ قطر مربع با اضلاع آن برابر نبوده و همیشه بزرگتر از آن است.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مربع — تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مربع چیست ؟ — تعریف و مفاهیم به زبان ساده (+ فیلم آموزش رایگان)
- قطر مربع چیست و چگونه بدست می آید ؟ — به زبان ساده + حل تمرین و مثال(همین مطلب)
- چگونه محیط مربع را حساب کنیم؟ + فیلم آموزشی و حل تمرین
- مساحت مربع چگونه بدست می آید؟ + فیلم آموزشی و حل تمرین و مثال
- طول ضلع مربع به محیط آن چیست؟ + حل تمرین و مثال
- فرمول محیط مربع چیست ؟ — به زبان ساده + حل تمرین و مثال
- فرمول مساحت مربع چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط مربع به صورت جبری — فرمول های ریاضی + حل تمرین و مثال
- مساحت مربع به صورت جبری — فرمول های ریاضی + حل تمرین و مثال
- مساحت مربع داخل دایره چگونه بدست می آید ؟ — به زبان ساده + تمرین و مثال
- مساحت مربع با قطر چگونه بدست می آید ؟ – به زبان ساده + حل تمرین و مثال











باسلام خدمت شما استاد گرامی یه قطر مربع 40*40سانتی متر قطر دایرش چقدر میشه هر چی حساب میکنم درست در نمیاد اگه لطف کنید بهم پاسخ بدین ممنون میشم
با سلام و عرض ادب و احترام. خسته نباشید. سپاس از مقاله عالی و درجه یک شما خیلی مفید بود. فقط یک سوال داشتم اگر قطر مربع ۱۰cm بود اندازه ضلع آن چه می شود؟
سلام و وقت بخیر؛
اگر اندازه قطر (d) را داشته باشیم، اندازه ضلع (a)، از رابطه a=√(d^2)/2 به دست میآید. برای قطر 10 سانتیمتر، اندازه ضلع برابر با رادیکال 50 خواهد بود.
از همراهی شما با مجله فرادرس سپاسگزاریم. سلامت و موفق باشید.