مساحت مستطیل به زبان ساده + فیلم آموزشی و حل تمرین

مساحت یک مستطیل، برابر با طول ضربدر عرض آن است. البته در صورت مشخص بودن قطر و یکی از ضلعهای مستطیل، میتوان مساحت آن را به کمک قضیه فیثاغورس محاسبه کرد. بسیاری از اجسام اطراف ما، دارای سطح مستطیلی شکل هستند. از اینرو، یادگیری نحوه اندازهگیری مساحت مستطیل میتواند باعث راحتتر شدن برخی از تصمیمگیریها شود. در این آموزش از مجله فرادرس، روشهای تعیین مساحت مستطیل را به همراه چند مثال کاربردی و واقعی توضیح میدهیم.
فیلم آموزشی محاسبه مساحت مستطیل
مساحت مستطیل چیست ؟
مساحت مستطیل، اندازه محدوده و سطحی است که درون ضلعهای مستطیل قرار میگیرد.
در تصویر زیر، بخش آبی رنگ، مساحت مستطیل را نمایش میدهد.

طول و عرض مستطیل چه هستند؟
برای اندازهگیری محدوده داخل محیط مستطیل، به طول، عرض یا قطر مستطیل نیاز دارید. مستطیل، یکی از شکلهای چند ضلعی است که از چهار ضلع و چهار راس تشکیل میشود. ضلعهای رو به رویی این شکل، با هم برابر هستند. به ضلعهای دارای اندازه بیشتر، «طول» میگویند. ضلعهای دارای اندازه کوچکتر نیز با عنوان «عرض» شناخته میشوند.
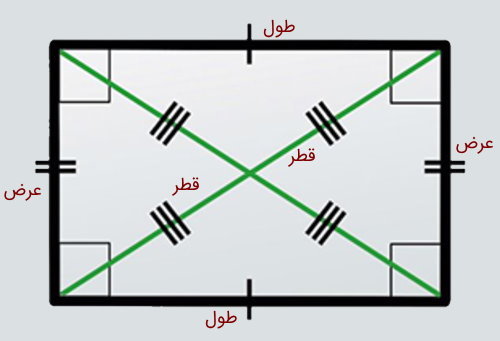
قطر مستطیل، پارهخطی است که دو راس رو به رویی را به یکدیگر متصل میکند. هر مستطیل، دو قطر با اندازههای برابر دارد.
مساحت مستطیل چگونه به دست می آید ؟
مساحت مستطیل، از ضرب طول در عرض مستطیل به دست میآید.
به همین دلیل، برای پیدا کردن مساحت این شکل، ابتدا باید اندازه طول و عرض آن را تعیین کرد.

رابطه مساحت مستطیل را میتوان به صورت زیر نوشت:
عرض طول = مساحت مستطیل
مثال: تعیین مساحت مستطیل
مستطیلی با طول 6 و عرض 5 را در نظر بگیرید. مساحت این مستطیل چقدر است؟
برای محاسبه مساحت مستطیل، رابطه زیر را مینویسیم:
عرض طول = مساحت مستطیل
سپس، اطلاعات مسئله را درون رابطه مساحت جایگذاری میکنیم:
۵ ۶ = مساحت مستطیل
30 = مساحت مستطیل
مساحت مستطیل مورد سوال برابر 30 است.
علامت ریاضی مساحت مستطیل چیست؟
مساحت مستطیل و دیگر شکلهای هندسی، معمولا با حرف انگلیسی A یا a نمایش داده میشود. این حرف، ابتدای کلمه «Area» به معنی «مساحت» است. حرف انگلیسی l یا L، ابتدای کلمه «طول» (Length)، برای نمایش طول مستطیل و حرف انگلیسی w یا W، ابتدای کلمه «عرض» (Width)، به منظور نشان دادن عرض مستطیل مورد استفاده قرار میگیرند.
فرمول مساحت مستطیل چیست ؟
فرمول ریاضی مساحت مستطیل، عبارت است از:
- A: مساحت
- l: طول
- w: عرض
واحد اندازه گیری مساحت مستطیل چیست؟
در سیستم بینالمللی، مساحت مستطیل با واحد میلیمتر مربع، سانتیمتر مربع، متر مربع و غیره بیان میشود.
مساحت مستطیل چه کاربردی دارد؟
در دنیای واقعی، بسیاری از وسایل و سازهها با سطح مستطیلی شکل ساخته میشوند. بخشهای مختلف ساختمان، لوازم خانگی، تجهیزات الکترونیکی و غیره، از مثالهای متداول اجسام مستطیلی شکل هستند. مساحت مستطیل، به عنوان یکی از محاسبات پایهای، در طراحی سازهها و وسایل مستطیلی شکل مورد استفاده قرار میگیرد.

روش های محاسبه مساحت مستطیل چه هستند؟
اندازه سطح داخل مستطیل با استفاده روش طول ضربدر عرض یا به کمک قضیه فیثاغورس محاسبه میشود. در صورت اندازهگیری یا دانستن مقدار طول و عرض، مساحت مستطیل از ضرب این دو مقدار به دست میآید.
در صورت دانستن قطر و یکی از مقادیر طول یا عرض، تعیین مساحت با استفاده از قضیه فیثاغورس انجام میگیرد. البته در صورت دانستن مختصات راسهای مستطیل، امکان پیدا کردن مساحت آن با محاسبات برداری نیز وجود دارد. در بخشهای بعدی، تمام این روشها را توضیح خواهیم داد.
حل مثال های مساحت مستطیل
در این بخش، به منظور آشنایی بهتر با نحوه محاسبه مساحت مستطیلها، به ارائه چند مثال کاربردی میپردازیم.
مثال اول: مساحت ابعاد میز مستطیلی شکل
دانش آموزشی قصد دارد اندازه سطح روی میز مطالعه خود را محاسبه کند. او برای این کار، ابتدا طول و عرض میز را توسط متر اندازه میگیرد. ابعاد اندازهگیری شده در تصویر زیر نمایش داده شدهاند. با توجه به این ابعاد، مساحت سطح میز را محاسبه کنید.
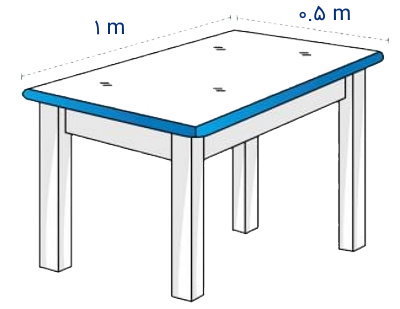
مطابق با رابطه مساحت مستطیل داریم:
عرض طول = مساحت مستطیل
طول میز برابر 1 متر و عرض آن برابر 0.5 متر است. این مقادیر را در رابطه بالا قرار میدهیم:
0.5 1 = مساحت سطح میز
0.5 = مساحت سطح میز
در نتیجه، مساحت سطح میز برابر 0.5 متر مربع است.
مثال دوم: مساحت پارچه مورد نیاز برای پرده
فردی میخواهد برای محدوده پنجره اتاق خود، پرده سفارش دهد. او برای این کار، به یک خیاط پرده مراجعه میکند. خیاط، شکل و ابعاد محدوده پنجره اتاق را از او میپرسد تا پارچه مورد نیاز برای دوخت پرده را تهیه کند. این اطلاعات در تصویر زیر نمایش داده شدهاند. مساحت پارچه مورد نیاز برای دوخت پرده چقدر است؟

مطابق با تصویر بالا، محدوده پنجره اتاق، به شکل مستطیل است. به همین دلیل، مساحت این محدوده از رابطه زیر به دست میآید:
عرض محدوده طول محدوده = مساحت محدوده پنجره
بر اساس اندازههای گرفته شده، طول محدوده برابر 1.8 متر و عرض آن برابر 1.5 متر است. این اعداد را درون رابطه بالا قرار میدهیم:
1.5 1.8 = مساحت محدوده پنجره
2.7 = مساحت محدوده پنجره
مساحت محدوده پنجره اتاق برابر 2.7 متر مربع است. به همین دلیل، خیاط، به بیشتر از 2.7 متر مربع پارچه برای دوخت پرده نیاز دارد. دلیل بیشتر بودن پارچه مورد نیاز، پوشاندن تمام محدوده پنجره است.
مثال سوم: مساحت قسمت رنگ شده مستطیل
تصویر زیر، یک مستطیل کوچک درون یک مستطیل بزرگ را نمایش میدهد. با توجه به اطلاعات نمایش داده شده در تصویر، مساحت قسمت رنگی مستطیل بزرگ را محاسبه کنید.
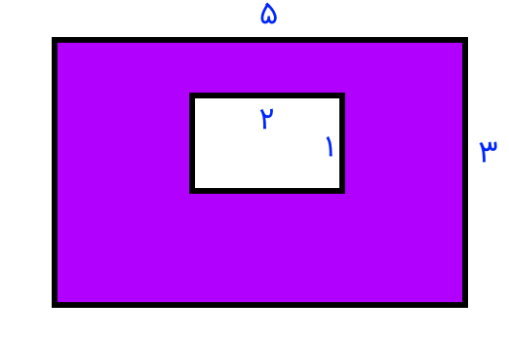
مساحت بخش رنگ شده در تصویر بالا برابر مساحت مستطیل بزرگ منهای مساحت مستطیل کوچک است. اطلاعات نمایش داده شده در این تصویر عبارت هستند از:
- طول مستطیل بزرگ: 5
- عرض مستطیل بزرگ: 3
- طول مستطیل کوچک: 2
- عرض مستطیل کوچک: 1
مساحت مستطیل بزرگ برابر است با:
عرض مستطیل بزرگ طول مستطیل بزرگ = مساحت مستطیل بزرگ
3 5 = مساحت مستطیل بزرگ
15 = مساحت مستطیل بزرگ
به همین ترتیب، مساحت مستطیل کوچک برابر است با:
عرض مستطیل کوچک طول مستطیل کوچک = مساحت مستطیل کوچک
1 2 = مساحت مستطیل کوچک
2 = مساحت مستطیل کوچک
در نتیجه:
مساحت مستطیل کوچک - مساحت مستطیل بزرگ = مساحت قسمت رنگی
2 - 15 = مساحت قسمت رنگی
13 = مساحت قسمت رنگی
مساحت قسمت رنگی برابر 13 است. این مثال در واقعیت کاربردهای گستردهای دارد. به عنوان مثال، اگر درون دیوار اتاق، یک تلویزیون تعبیه شده باشد، مساحت باقیمانده دیوار از تفریق مساحت دیوار و مساحت تلویزیون به دست میآید. به این ترتیب، در صورت تمایل به افزودن وسایل دیگر (مانند قفسه)، تهیه کاغذ دیواری و غیره، مساحت موجود بر روی دیوار مشخص میشود.

مثال چهارم: تعداد شیرینی در سینی
تصویر زیر، یک سینی مستطیلی شکل را نمایش میدهد. اگر بخواهیم این سینی را با شیرینیهای مستطیلی شکل پر کنیم، تعداد شیرینیها چقدر خواهد بود؟

اطلاعات مسئله عبارت هستند از:
- طول سینی: 30 سانتیمتر
- عرض سینی: 10 سانتیمتر
- طول سطح شیرینی: 3 سانتیمتر
- عرض سطح شیرینی: 2 سانتیمتر
تعداد شیرینیهای سینی، از تقسیم مساحت سینی بر مساحت شیرینیها به دست میآید. برای این کار، ابتدا مساحت سینی را محاسبه میکنیم:
عرض سینی طول سینی = مساحت سینی
10 30 = مساحت سینی
300 = مساحت سینی
مساحت سینی برابر 300 سانتیمتر مربع است. اکنون، مساحت سطح پایینی یک عدد شیرینی را به دست میآوریم:
عرض شیرینی طول شیرینی = مساحت شیرینی
2 3 = مساحت شیرینی
6 = مساحت شیرینی
مساحت شیرینی برابر 30 سانتیمتر مربع است. با تقسیم مساحت سینی بر شیرینی، ظرفیت سینی مشخص میشود:
مساحت شیرینی ÷ مساحت سینی = حداکثر تعداد شیرینی در سینی
6 ÷ 300 = حداکثر تعداد شیرینی در سینی
50 = حداکثر تعداد شیرینی در سینی
در نتیجه، میتوان حداکثر 50 شیرینی درون سینی مستطیلی شکل جای داد.
مثال پنجم: تعیین زمین بزرگتر
شخصی قصد دارد از میان دو زمین مستطیلی شکل، بزرگترین زمین را برای ساخت خانه انتخاب کند. اطلاعات این زمینها در ادامه آورده شده است.
- زمین 1
- طول زمین 1: 15 متر
- عرض زمین 1: 10 متر
- زمین 2
- طول زمین 2: 13 متر
- عرض زمین 2: 12 متر
انتخاب این شخص کدام گزینه خواهد بود؟
برای مقایسه اندازه دو زمین، مساحت هر یک از آنها را محاسبه میکنیم:
عرض زمین 1 طول زمین 1 = مساحت زمین 1
10 15 = مساحت زمین 1
150= مساحت زمین 1
مساحت زمین 1 برابر 150 متر مربع است. برای زمین 2، داریم:
عرض زمین 2 طول زمین 2 = مساحت زمین 2
12 13 = مساحت زمین 2
156 = مساحت زمین 2
مساحت زمین 2 برابر 156 متر مربع است. در نتیجه، این زمین انتخاب میشود.
مثال ششم: تعیین مساحت مستطیل با استفاده از محیط
در تصویر زیر، یک مستطیل با محیط 18 و طول 5 نمایش داده شده است. با توجه به این اطلاعات، مساحت سطح داخل محیط را تعیین کنید.
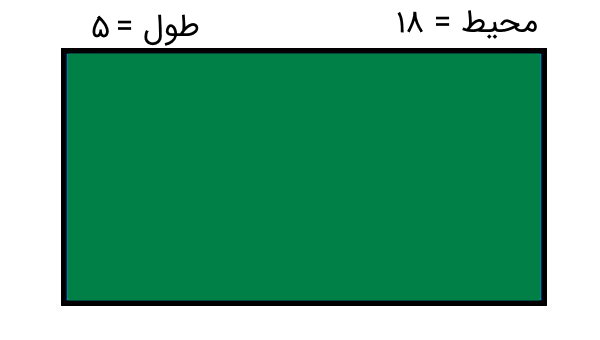
محیط مستطیل برابر مجموع طول و عرض ضربدر دو است. به عبارت دیگر:
(عرض مستطیل + طول مستطیل) 2 = محیط مستطیل
(عرض مستطیل + 5) 2 = 18
عرض مستطیل + 5 = 2 ÷ 18
عرض مستطیل + 5 = 9
عرض مستطیل = 5 - 9
عرض مستطیل = 4
عرض مستطیل برابر 4 است. اکنون، با داشتن مقدار طول و عرض مستطیل، میتوانیم مساحت آن را با استفاده از رابطه زیر تعیین کنیم:
عرض مستطیل طول مستطیل = مساحت مستطیل
4 5 = مساحت مستطیل
20 = مساحت مستطیل
در نتیجه، مساحت مستطیلی با محیط 18 و طول 5، برابر 20 خواهد بود.
مساحت مستطیل با قطر یا قضیه فیثاغورس
محاسبه مساحت مستطیل با قطر و یکی از ضلعهای مستطیل، به کمک قضیه فیثاغورس انجام میگیرد.
در مستطیل، تمام راسها دارای زاویه 90 درجه هستند. به همین دلیل، در صورت رسم قطر، مستطیل به دو مثلث قائم الزاویه تبدیل میشود.
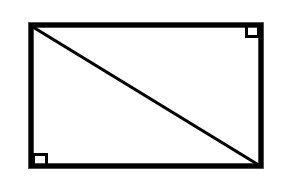
قضیه فیثاغورس در مثلثهای قائم الزاویه، به صورت زیر بیان میشود:
- a: یکی از ساقهای مثلث قائم الزاویه
- b: ساق دیگر مثلث قائم الزاویه
- c: وتر مثلث قائم الزاویه
تصویر زیر، معادل پارامترهای بالا را در یک مستطیل نمایش میدهد.
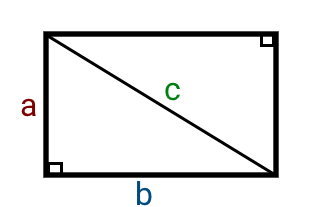
قضیه فیثاغورس برای مستطیل بالا، عبارت است:
2(عرض) + 2(طول) = 2(قطر مستطیل)
در صورت دانستن مقدار قطر و یک از ضلعها، ضلع دیگر مستطیل با استفاده از رابطه بالا، قابل محاسبه خواهد بود. به این ترتیب، مساحت مستطیل مورد نظر با ضرب طول در عرض آن به دست میآید.
فرمول مساحت مستطیل با قطر
در کتابها و منابع آموزشی، قطر اشکال هندسی با حرف انگلیسی d نمایش داده میشود. بر این اساس، فرم ریاضی رابطه بالا به شکل زیر در میآید:
- l: طول مستطیل
- w: عرض مستطیل
- d: قطر مستطیل
اگر رابطه بالا را بر حسب طول بازنویسی کنیم، خواهیم داشت:
فرمول کلی مساحت مستطیلها برابر است با:
فرمول به دست آمده برای طول را در رابطه بالا قرار میهیم:
به همین ترتیب، خواهیم داشت:
رابطههای بالا، به منظور محاسبه مستقیم مساحت مستطیل با طول و یکی از ضلعها مورد استفاده قرار میگیرد.
مثال: محاسبه سطح مستطیل با قطر
مساحت مستطیلی با عرض 3 سانتیمتر و قطر 5 سانتیمتر را محاسبه کنید.
مساحت مستطیلها از ضرب طول در عرض به دست میآید. در صورت سوال، به جای مقدار طول، مقدار قطر بیان شده است. به همین دلیل، دو روش برای تعیین مساحت داریم. در روش اول، ابتدا طول مستطیل به وسیله قضیه فیثاغورس محاسبه میشود. مطابق قضیه فیثاغورس داریم:
- l: طول مستطیل
- w: عرض مستطیل و برابر 3 سانتیمتر
- d: قطر مستطیل و برابر 5 سانتیمتر
مقادیر اطلاعات سوال را درون رابطه بالا قرار میدهیم:
طول مستطیل برابر 4 سانتیمتر است. با جایگذاری این مقدار در رابطه کلی مساحت مستطیل، خواهیم داشت:
مساحت مستطیل مورد سوال برابر 12 سانتیمتر مربع است. در روش دوم، میتوانستیم از رابطه مستقیم برای محاسبه مساحت مستطیل با قطر استفاده کنیم. مطابق این رابطه و اطلاعات مسئله داریم:
- A: مساحت
- d: قطر مستطیل و برابر 5 سانتیمتر
- w: عرض مستطیل و برابر 3 سانتیمتر
مقادیر موجود را درون فرمول جایگذاری میکنیم:
همان طور که مشاهده میکنید، تعداد عملیاتهای محاسباتی مورد نیاز با استفاده از روش دوم کمتر است.
مساحت مستطیل متشابه
نسبت مساحتهای دو مستطیل متشابه، برابر با نسبت ضلعهای منتظر آنها به توان دو است.
مستطیلهای متشابه، مستطیلهای هستند که نسبت عرضها آنها برابر نسبت طول آنها است. دو مستطیل ABCD و EFGH را در نظر بگیرید.
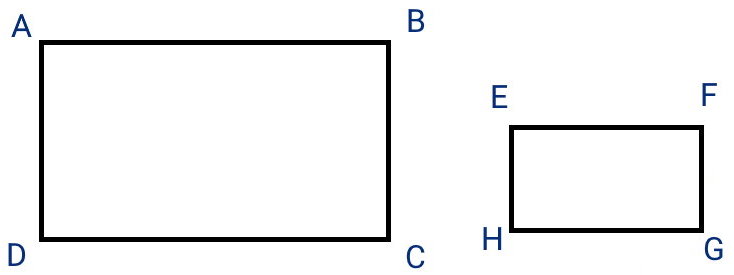
نسبت مساحتهای دو مستطیل با به صورت زیر بیان میشود:
مثال اول: تعیین مساحت مستطیلهای متشابه
تصویر زیر، دو مستطیل متشابه را نمایش میدهد. با توجه به اطلاعات نمایش داده شده، مساحت مستطیل EFGH را محاسبه کنید.
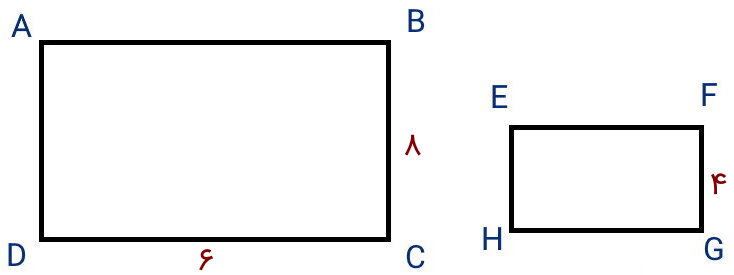
در تصویر بالا، مقدار طول و عرض مستطیل ABCD و مقدار طول مستطیل EFGH بیان شده است. به همین دلیل، فقط میتوانیم مساحت مستطیل ABCD را محاسبه کنیم. مطابق با فرمول مساحت مستطیل، داریم:
فرمول بالا را برای مستطیل ABCD بازنویسی میکنیم:
طول ضلع BC برابر 8 سانتیمتر و طول ضلع CD برابر 6 سانتیمتر است. این عددها را در رابطه بالا قرار میدهیم:
در نتیجه، مساحت مثلث ABCD برابر 48 سانتیمتر مربع است.
طبق رابطه بین مساحتهای دو مستطیل متشابه، داریم:
بر اساس تصویر مسئله، مقدار ضلع FG برابر 4 سانتیمتر است. این مقدار را به همراه مساحت به دست آمده از مرحله قبل و طول ضلع BC در رابطه بالا میگذاریم:
در نتیجه، مساحت مستطیل EFGH برابر 12 سانتیمتر مربع است. همانطور که مشاهده میکنید، با نصف شدن طول ضلعهای متناظر (8 سانتیمتر و 4 سانتیمتر)، مساحت، یک چهارم شد.
مثال دوم: تعیین طول ضلع فرشهای متشابه بر اساس مساحت
دو فرش ماشینی متشابه با مساحتهای 4 متر مربع و 6 متر مربع را در نظر بگیرید. اگر طول فرش 6 متر مربعی برابر 3 متر باشد، طول فرش 4 متر مربعی چقدر خواهد بود؟
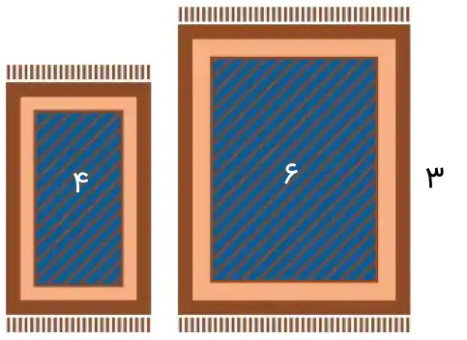
مطابق با رابطه بین مساحتهای دو مستطیل مشابه، داریم:
رابطه بالا را برای بر اساس اطلاعات این مسئله بازنویسی میکنیم:
- A6: مساحت فرش 6 متر مربعی
- A4: مساحت فرش 4 متر مربعی
- l6: طول فرش 6 متر مربعی
- l4: طول فرش 4 متر مربعی
اعداد موجود را در رابطه بالا قرار میدهیم:
رابطه بالا را طرفین و وسطین میکنیم:
اکنون، رابطه را بر حسب طول فرش 4 متری مینویسیم:
بر اساس محاسبات انجام شده، طول فرش 4 متر مربعی برابر 2.45 متر است.
نکته: در واقعیت، مساحت فرشهای معروف به 4 متری، مقداری کمتر از 4 متر مربع بوده و فرض مساحت 4 متر مربع برای سادگی محاسبات در نظر گرفته شده است.
مساحت مستطیل با سه راس
یکی از روشهای محاسبه مساحت یک محدوده مستطیلی شکل، استفاده از مختصات راسهای مستطیل است.
استفاده از این روش، به آشنایی با مفهوم دستگاه مختصات و محاسبات برداری (جمع بردار و اندازه بردار) نیاز دارد. اگر یک مستطیل را بر روی دستگاه مختصات در نظر بگیریم، تمام راسهای آن، مانند یک نقطه، دارای مختصات هندسی در صفحه دو بعدی یا فضای سه بعدی خواهند بود.
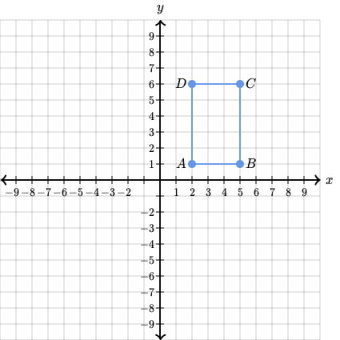
تصویر بالا، یک مستطیل را در دستگاه مختصات دو بعدی نمایش میدهد. به منظور درک بهتر ابعاد، این دستگاه بر روی یک شبکه شطرنجی رسم شده است. راسهای مستطیل ABCD دارای مختصات زیر در دستگاه بالا هستند:
- راس A با مختصات (2,1)
- راس B با مختصات (5,1)
- راس C با مختصات (5,6)
- راس D با مختصات (1,6)
با استفاده از راسهای مجاور، میتوان ابعاد هر یک از ضلعهای مستطیل را محاسبه کرد. به عنوان مثال، ضلع AB را در نظر بگیرید. این ضلع از دو راس A و B تشکیل میشود. مطابق با خانههای شطرنجی، طول ضلع AB برابر 3 است. به منظور تعیین این طول بر اساس مختصات راسها، ابتدا باید بردار منطبق بر روی این دو راس را تعیین میکنیم. این کار به صورت زیر انجام میشود:
- : بردار معرف ضلع AB
- B: مختصات راس B
- A: مختصات راس A
مقادیر را درون رابطه بالا جایگذاری میکنیم:
اندازه این بردار، همان طول ضلع AB است. مطابق با رابطه اندازه بردار، داریم:
در نتیجه، اندازه ضلع AB برابر 3 است. با استفاده از همین روش، اندازه یکی از ضلعهای مجاور را به دست میآوریم. این اندازه در مثال بالا برابر 5 است. به این ترتیب، طول و عرض مستطیل به دست میآید. در نهایت، با ضرب طول در عرض، مساحت مستطیل محاسبه میشود.
مثال: تعیین سطح مستطیل با سه راس
مساحت مستطیلی با راسهای زیر را محاسبه کنید:
- راس اول با مختصات (3-,4-)
- راس دوم با مختصات (4,1-)
- راس سوم با مختصات (3,1)
محل تقریبی راسهای بالا را بر روی محور مختصات مشخص میکنیم. این کار، به منظور تشخیص ضلعها انجام میهیم.

مطابق با تصویر، این مختصاتها میتوانند معرف ضلعهای AB و BC مستطیل مورد سوال باشند. راسهای بالا را به صورت زیر یادداشت میکنیم:
- (3-,4-)A
- (4,1-)B
- (3,1)C
طول ضلع AB به صورت زیر محاسبه میشود:
طول ضلع AB برابر با 4 است. محاسبه طول ضلع BC نیز به صورت زیر انجام میگیرد:
طول ضلع BC برابر 7 است. به این ترتیب، ضلع AB، عرض مستطیل و ضلع BC، طول مستطیل خواهد بود. مطابق با رابطه مساحت مستطیل داریم:
عرض طول = مساحت مستطیل
4 7 = مساحت مستطیل
28 = مساحت مستطیل
مساحت مستطیل برابر 28 است. از کاربردهای اصلی روش محاسبه مساحت با سه راس، میتوان به تعیین مساحت زمینهای مستطیلی شکل با استفاده از مختصات نرم افزارهایی مانند گوگل ارث و گوگل مپ اشاره کرد. برای بررسی این موضوع، میتوانید مساحت زمین خانه خود را با پیدا کردن مختصات گوشههای آن در این نرم افزارها محاسبه کنید.
مساحت مستطیل در محاسبه حجم مکعب مستطیل کاربرد دارد. به منظور آشنایی با این محاسبات، مطالعه مطلب «حجم مکعب مستطیل چیست؟ — به زبان ساده + حل تمرین و مثالهای متنوع» از مجله فرادرس را به شما پیشنهاد میکنیم.
سخن آخر: محاسبه آنلاین مساحت مستطیل
در بخشهای قبلی، روشهای محاسبه دستی مساحت مستطیلها را توضیح دادیم. ابزارهای اینترنتی مختلفی برای انجام این محاسبات وجود دارند.
از شناخته شدهترین سایتهای محاسبه آنلاین مساحت مستطیل میتوان به موارد زیر اشاره کرد:
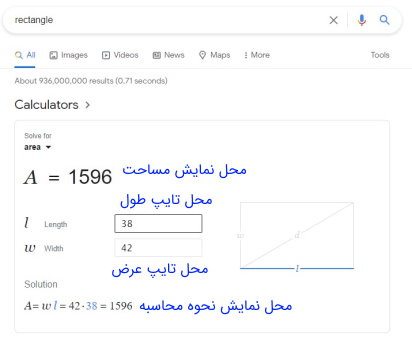
مطابق تصویر زیر، با جستجوی عبارت «rectangle» یا «rectangle area» در سایت گوگل، وارد کردن طول مستطیل در مقابل کادر «l» و وارد کردن عرض آن در مقابل کادر «w»، مساحت مستطیل محاسبه و نمایش داده میشود.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش های بدست آوردن محیط و مساحت مستطیل + حل تمرین و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مستطیل چیست ؟ — تعریف و مفاهیم به زبان ساده + فیلم آموزش رایگان
- طول و عرض مستطیل چیست و چگونه بدست می آید ؟ + حل تمرین و مثال
- قطر مستطیل چیست و چه خواصی دارد؟ — فرمول های محاسبه + حل مثال
- محیط مستطیل چگونه بدست می آید؟ + فیلم آموزشی و حل تمرین و مثال
- مساحت مستطیل به زبان ساده + فیلم آموزشی و حل تمرین(همین مطلب)
- حجم مکعب مستطیل چیست ؟ — به زبان ساده + حل تمرین و مثال های متنوع
- رابطه محیط و مساحت مستطیل — معرفی فرمول ها + حل تمرین و مثال
- فرمول محیط مستطیل چیست ؟ — به زبان ساده + حل مثال
- فرمول مساحت مستطیل چیست ؟ — به زبان ساده + حل مثال
- محیط مستطیل به صورت جبری — فرمول های محیط مستطیل + حل تمرین و مثال
- مساحت مستطیل به صورت جبری — فرمول های ریاضی + حل مثال
- محیط مستطیل کسری چگونه بدست می آید ؟ + حل تمرین و مثال
- مساحت مستطیل کسری چگونه بدست می آید ؟ — حل تمرین و مثال













استاد سراج ممنونم. برایتان موفقیت آرزو دارم.
کاظم.
عالی بود.ممنونم از مدرس ارجمند.
اگه نسبت طول به عرض یه مستطیل 4 به 8 باشه و محیط ان 120
مساحت ان چقدر است ؟
سلام.
احتمالاً منظورتان این است که نسبت طول به عرض ۸ به ۴ است. فرض کنید طول a و عرض b باشد. با توجه به نسبت طول به عرض داریم: ba=48 و این یعنی a=2b. همچنین، با توجه به اینکه محیط را داریم، میتوان نوشت: 2(a+b)=120. بنابراین، رابطه a+b=60 را نیز داریم. اکنون، از دو تساوی a=2b و a+b=60 اندازه طول و عرض را محاسبه میکنیم. با توجه به a=2b، میتوان رابطه 2b+b=3b=60 را نوشت که از آن، b=20 به دست میآید. در نتیجه، a=40 است. در نهایت، مساحت مستطیل برابر است با S=a×b=20×40=800.
موفق باشید.
مساحت مستطیل برابر است با چی؟؟
سلام، وقت شما بخیر؛
بخش مربوط به فرمول مساحت مستطیل را اگر در مطلب مطالعه کنید این موضوع به صورت کامل و به زبان بسیار ساده شرح داده شده است.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.