قطر مستطیل چیست و چه خواصی دارد؟ — فرمول های محاسبه + حل مثال

قطر مستطیل پاره‌خطی است که گوشه‌های روبه‌روی آن را به یکدیگر وصل می‌کند. برای هر مستطیل، می‌توان دو قطر با اندازه‌های برابر رسم کرد. اندازه این قطرها از قضیه فیثاغورس به دست می‌آید. به علاوه، با داشتن این اندازه و اندازه یکی از ضلع‌ها، امکان تعیین محیط و مساحت مستطیل فراهم می‌شود. در این آموزش از مجله فرادرس، به معرفی خواص، فرمول‌ها و اثبات یکی از خواص قطر مستطیل به همراه حل چندین مثال متنوع می‌پردازیم. علاوه بر این، در انتهای آموزش، به برخی از پرتکرارترین سوالات در رابطه با قطر مستطیل پاسخ می‌دهیم.

قطر چیست؟

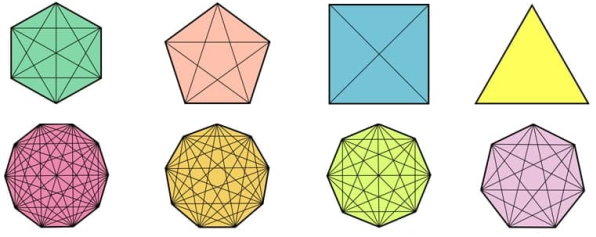
در شکل‌های هندسی چندضلعی مانند مربع، مستطیل، لوزی و غیره، اگر گوشه‌های مقابل را توسط یک پاره‌خط به هم وصل کنیم، قطر شکل به دست می‌آید.

تصویر زیر، قطرهای برخی از چندضلعی‌های منتظم را نمایش می‌دهد.

مستطیل چیست؟

مستطیل، یک شکل چهار ضلعی است. ضلع‌های رو به رویی این شکل با هم‌اندازه هستند. به علاوه، ضلع‌های مجاور، یکدیگر را با زاویه راست قطع می‌کنند. در واقع، مستطیل، متوازی الاضلاعی است که تمام گوشه‌های آن، زاویه 90 درجه دارند.

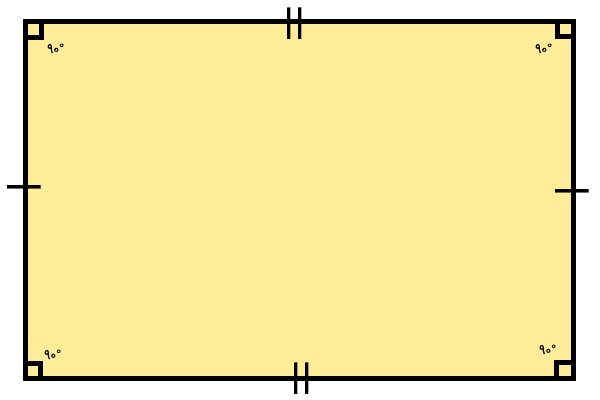
اجزای مستطیل چه هستند؟

از مهم‌ترین اجزای مستطیل در کنار ضلع و گوشه‌های آن می‌توان به زاویه‌های داخلی، زاویه‌های خارجی و قطرها اشاره کرد. این اجزا، به منظور محاسبه اندازه‌های مهم مستطیل نظیر محیط و مساحت آن مورد استفاده قرار می‌گیرند. به طور کلی، طول و عرض (ضلع‌های بزرگ و ضلع‌های کوچک) مستطیل، اندازه‌های اصلی در محاسبه محیط و مساحت هستند. با این وجود، امکان تعیین محیط و مساحت با قطر نیز وجود دارد.

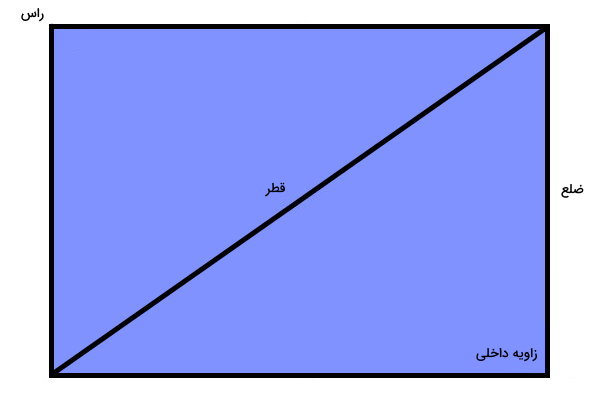
قطر مستطیل چیست؟

پاره‌خطی که دو گوشه غیر مجاور مستطیل را به یکدیگر وصل می‌کند، با عنوان «قطر» شناخته می‌شود. پاره خط (الف ج)، یکی از قطرهای مستطیل است.

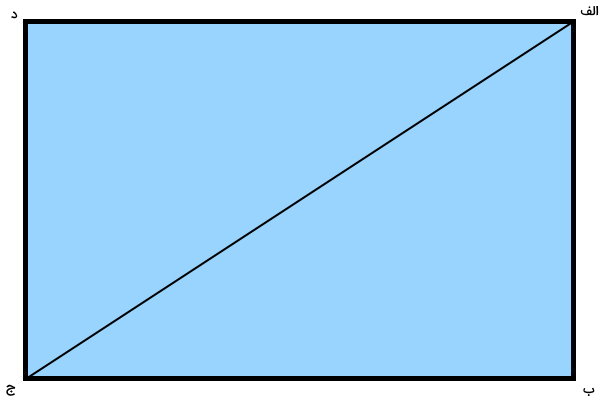
همان‌طور که مشاهده می‌کنید، امکان رسم یک پاره خط دیگر از گوشه (ب) تا گوشه (ج) وجود دارد. این پاره خط، قطر دوم مستطیل خواهد بود. به این ترتیب، هر مستطیل می‌تواند دو قطر داشته باشد. در بخش بعدی، به معرفی ویژگی‌های این دو قطر می‌پردازیم.

ویژگی های قطر مستطیل چه هستند؟

برخی از مهم‌ترین خواص قطرهای مستطیل در زیر آورده شده‌اند:

• اندازه قطرهای مستطیل، برابر است.
• قطرهای مستطیل، یکدیگر را به دو قسمت مساوی تقسیم می‌کنند. به عبارت دیگر، قطرهای مستطیل، منصف یکدیگرند.
• هر قطر مستطیل، آن را به دو مثلث قائم الزاویه مساوی تبدیل می‌کند. به عبارت دیگر، با رسم قطر مستطیل، دو مثلث با مساحت‌های برابر تشکیل می‌شود.
• اندازه قطرهای مستطیل با استفاده از قضیه فیثاغورس به دست می‌آید.
• در محل برخورد قطرهای مستطیل، دو زاویه حاده (کمتر از 90 درجه) و دو زاویه منفرجه (بیشتر از 90 درجه) به وجود می‌آید. به عبارت دیگر، قطرهای مستطیل، همدیگر را با زاویه 90 درجه قطع نمی‌کنند (عمود بر یکدیگر نیستند).
• مستطیلی که قطرهای آن عمود بر یکدیگر هستند، با عنوان مربع شناخته می‌شود.

مثال 1: رسم قطرهای مستطیل

مستطیلی دارای طول 12 سانتی‌متر و عرض 5 سانتی‌متر است. قطرهای مستطیل را رسم کنید.

بهترین ابزار برای رسم مستطیل، گونیا است. با استفاده از این ابزار، امکان رسم دو خط عمود بر هم فراهم می‌شود. به کمک گونیا، مستطیلی را رسم و گوشه‌های آن را نام‌گذاری می‌کنیم.

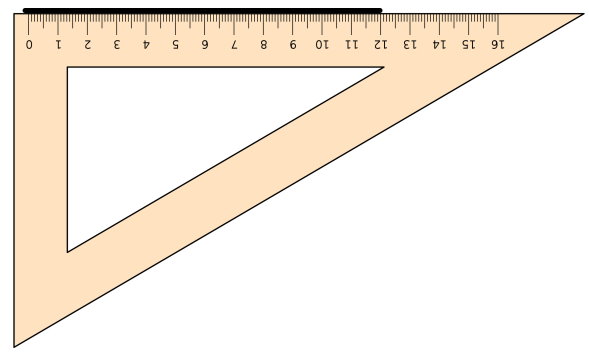
ضلع‌های کوچک (5 سانتی‌متر)، عرض مستطیل و ضلع‌های بزرگ (12 سانتی‌متر)، طول مستطیل را نمایش می‌دهند.

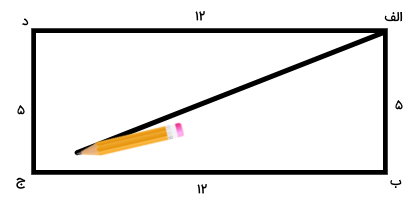
به منظور رسم قطرهای مستطیل، مداد خود را بر روی یکی از گوشه‌ها (مانند گوشه الف) قرار می‌دهیم. سپس، پاره‌خطی را از آن گوشه به گوشه مقابل (مانند گوشه ج) رسم می‌کنیم.

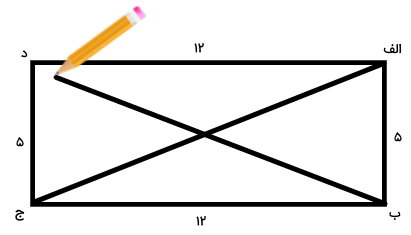
اکنون، مداد را بر روی گوشه (ب) قرار می‌دهیم و یک پاره‌خط تا گوشه (د) می‌کشیم. به این ترتیب، هر دو قطر مستطیل را رسم کردیم.

مثال 2: تعیین اندازه بخش های مختلف قطر مستطیل

مستطیل رسم شده در مثال قبلی را در نظر بگیرید. اندازه قطرهای این مستطیل برابر با 13 سانتی‌متر است. بخش‌های مختلف قطر را با علامت سوال مشخص کرده‌ایم. به جای علامت سوال، عدد مناسب قرار دهید.

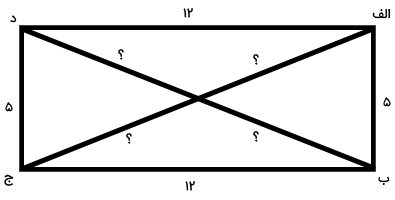
اندازه هر قطر مستطیل بالا برابر 13 سانتی‌متر است. می‌دانیم که قطرهای مستطیل، همدیگر را نصف می‌کنند. بنابراین، اندازه علامت سوال‌های روی هر بخش مستطیل، برابر با نصف قطر، یعنی 6/5 سانتی‌متر است.

قطر مستطیل چگونه محاسبه می شود ؟

قطر مستطیل با استفاده از قضیه فیثاغورس در مثلث‌های قائم الزاویه محاسبه می‌شود. مثلث قائم الزاویه زیر را در نظر بگیرید.

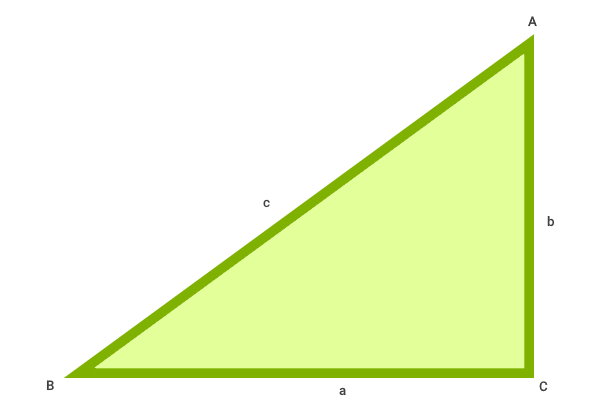
در مثلث بالا، بین وتر و ساق‌های مثلث ABC، رابطه زیر برقرار است:

$$
c^2 = a^2 + b^2
$$

• c: وتر
• a: ساق اول
• b: ساق دوم

به این رابطه، قضیه فیثاغورس می‌گویند. اکنون، مستطیل ABCD را در نظر بگیرد. مطابق با تصویر زیر، قطر AC در این مستطیل را رسم می‌کنیم.

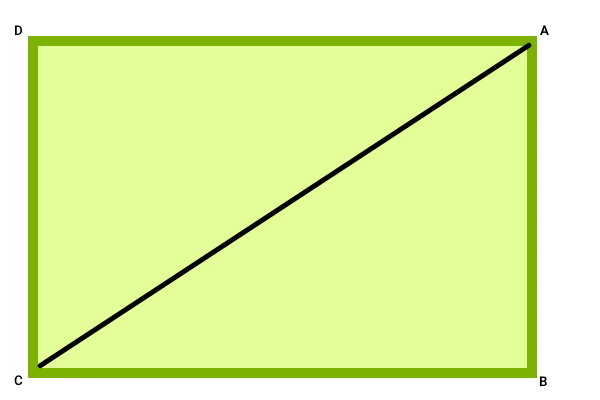
همان‌طور که مشاهده می‌کنید، با رسم قطر AC، مستطیل ABCD به دو مثلث ABC و ADC تبدیل می‌شود. اندازه زاویه گوشه‌های هر مستطیل برابر با 90 درجه است. بنابراین، مثلث‌های تشکیل شده در تصویر بالا، قائم الزاویه هستند و از قضیه فیثاغورس پیروی می‌کنند. به عنوان مثال، رابطه فیثاغورس برای مثلث ABC به صورت زیر خواهد بود:

$$
AC^2 = AB^2 + BC^2
$$

• AC: قطر مستطیل
• AB: عرض مستطیل
• BC: طول مستطیل

در ریاضیات، قطر مستطیل، معمولا با حرف d، عرض مستطیل با حرف w و طول مستطیل با حرف l نمایش داده می‌شود. بر این اساس، فرمول قطر مستطیل عبارت است از:

$$
d^2 = w^2 + l^2
$$

مثال 3: محاسبه قطر مستطیل از روی طول و عرض

طول یک مستطیل برابر با 12 سانتی‌متر و عرض آن برابر 5 سانتی‌متر است. اندازه قطر مستطیل را به دست بیاورید.

برای حل مسئله، رابطه قطر مستطیل با ضلع را می‌نویسیم:

$$
d^2 = w^2 + l^2
$$

• d: قطر مستطیل
• w: عرض مستطیل برابر 5 سانتی‌متر
• l: طول مستطیل برابر 12 سانتی‌متر

$$
d^2 = 5^2 + 12^2
$$

$$
d^2 = 25 + 144
$$

$$
d^2 = 169
$$

$$
d= \sqrt {169}
$$

$$
d= 13
$$

در نتیجه، قطر مستطیل برابر 13 سانتی‌متر است.

محاسبه محیط مستطیل با قطر

محیط مستطیل، با استفاده از فرمول‌های زیر محاسبه می‌شود:

(عرض × 2) + (طول × 2) = محیط مستطیل

(عرض + طول) × 2 = محیط مستطیل

بر اساس فرمول‌های بالا، به منظور محاسبه محیط مستطیل، به اندازه طول و عرض آن نیاز داریم. در بخش قبلی دیدیم که ضلع‌ها و قطرهای مستطیل، از قضیه فیثاغورس پیروی می‌کنند. از این‌رو، اگر اندازه یکی از ضلع‌ها و قطر مستطیل مشخص باشد، می‌توانیم اندازه ضلع دوم و سپس محیط مستطیل را به دست بیاوریم. فرمول ریاضی محیط مستطیل با قطر به صورت زیر نوشته می‌شود:

$$
P=2 a+2 \sqrt{d^{2}-a^{2}}
$$

• P: محیط مستطیل
• a: یکی از ضلع‌های مستطیل
• d: قطر مستطیل

مثال 4: محاسبه طول و محیط مستطیل از روی قطر و عرض

طول مستطیلی به قطر 17 و عرض 8 را حساب کنید. سپس، محیط آن را به دست بیاورید.

به منظور محاسبه عرض مستطیل، قضیه فیثاغورس را می‌نویسیم:

$$
d^2 = w^2 + l^2
$$

• d: قطر برابر 17
• w: عرض برابر 8
• l: طول

$$
17^2 = w^2 + 8^2
$$

$$
289 = w^2 + 64
$$

$$
w^2 = 289 -64
$$

$$
w^2 = 225
$$

$$
w = \sqrt {22}
$$

$$
w = 15
$$

طول مستطیل برابر 15 است. اکنون اندازه‌های طول و عرض را درون فرمول محیط قرار می‌دهیم:

(عرض × 2) + (طول × 2) = محیط مستطیل

(8 × 2) + (15 × 2) = محیط مستطیل

(16) + (30) = محیط مستطیل

46 = محیط مستطیل

در نتیجه، محیط مستطیل برابر 46 است. در این مثال، محیط را به صورت مرحله‌ای به دست آوردیم. در صورت استفاده از فرمول مخصوص محاسبه محیط مستطیل با قطر نیز به همین جواب می‌رسیم.

محاسبه مساحت مستطیل با قطر

در صورت مشخص بودن اندازه طول و عرض مستطیل، مساحت آن با استفاده از فرمول زیر محاسبه می‌شود:

عرض × طول = مساحت مستطیل

اگر اندازه قطر و یکی از ضلع‌های مستطیل را داشته باشیم، می‌توانیم از فرمول زیر برای محاسبه مساحت استفاده کنیم:

$$
A=a \sqrt{d^{2}-a^{2}}
$$

• A: مساحت
• a: یکی از ضلع‌ها
• d: قطر

مشابه فرمول محیط مستطیل از روی قطر، فرمول بالا نیز با کمک قضیه فیثاغورس نوشته شده است.

مثال 5: محاسبه عرض و مساحت مستطیل از روی قطر و طول

قطر یک مستطیل برابر 9 متر و طول آن برابر 7 متر است. مساحت و عرض مستطیل را حساب کنید. (رادیکال 2 را برابر 1/4 در نظر بگیرید.)

به منظور تعیین مساحت مستطیل با قطر، فرمول مخصوص به آن را می‌نویسیم:

$$
A=a \sqrt{d^{2}-a^{2}}
$$

• A: مساحت
• a: یکی از ضلع‌ها برابر 7 متر
• d: قطر برابر * متر

$$
A=7 \times \sqrt{9^{2}-7^{2}}
$$

$$
A=7 \times \sqrt{81-49}
$$

$$
A=7 \times \sqrt{32}
$$

$$
A=7 \times \sqrt{2\times 16}
$$

$$
A=7 \times 4\sqrt{2}
$$

$$
A=28\sqrt{2}
$$

$$
A=28\times 1.4
$$

$$
A=39.2
$$

در نتیجه، مساحت مستطیل برابر 39/2 است.

اثبات برابر بودن قطرهای مستطیل

به منظور اثبات برابر بودن قطرهای مستطیل، از مفهوم هم‌نهشتی مثلث‌ها استفاده می‌کنیم. اگر دو مثلث، دارای اندازه‌های یکسان باشند، به آن دو مثلث، هم‌نهشت می‌گویند.

مستطیل ABCD را در نظر بگیرید. در این مستطیل، یک بار قطر AC و یک بار قطر BD آن را رسم می‌کنیم. برای اثبات برابر بودن قطرهای مستطیل، حالت‌های هم‌نهشتی را برای مثلث‌های ABC و DCB مورد بررسی قرار می‌دهیم.

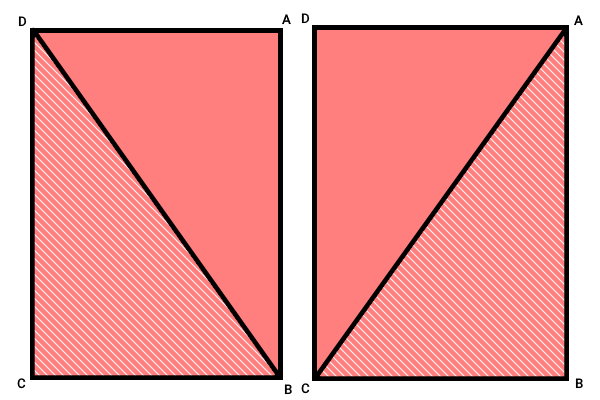
حالت‌های مختلف هم‌نهشتی مثلث‌ها عبارت هستند از:

• سه ضلع (ض ض ض)
• دو ضلع و زاویه بین (ض ز ض)
• دو زاویه و ضلع بین (ز ض ز)
• دو زاویه و یک ضلع (ض ض ز)

اگر هر یک از حالت‌های بالا بین دو مثلث برقرار باشند، آن دو مثلث، هم‌نهشت خواهند بود. در مستطیل ABCD، داریم:

$$
AB_{ ABC } = DC_{ DCB }
$$

$$
BC_{ ABC } = BC_{ DCB }
$$

$$
\hat{B}=\hat{C}=90^{\circ}
$$

به این ترتیب، دو ضلع و زاویه بین در مثلث‌های ABC و DCB با هم برابرند. در نتیجه، این مثلث‌ها، هم‌نهشت هستند. هم‌نهشتی ABC و DCB، نشان‌دهنده برابر بودن AC و DB یا همان قطرهای مستطیل است. بر اساس هم این استدلال و با استفاده از حالت هم نهشتی (ض ز ض) می‌توانیم اثبات کنیم که قطرهای مستطیل همدیگر را نصف می‌کنند.

سوالات متداول در رابطه با قطر مستطیل

در این مطلب از مجله فرادرس فهمیدیم قطر مستطیل چیست و چگونه محاسبه می‌شود. در این بخش، به برخی از سوالات پرتکرار در رابطه با قطرهای مستطیل به طور خلاصه پاسخ می‌دهیم.

مستطیل چند قطر دارد ؟

مستطیل دو قطر دارد.

آیا قطرهای مستطیل با هم برابرند ؟

بله. مستطیل، دارای دو قطر هم‌اندازه است.

چرا قطرهای مستطیل با هم برابرند ؟

بر اساس حالت هم نهشتی دو ضلع و زاویه بین یا (ض ز ض)، قطرهای مستطیل با هم برابر هستند.

آیا قطرهای مستطیل بر هم عمودند ؟

خیر. در حالت کلی، قطرهای مستطیل بر هم عمود نیستند؛ اما اگر قطرهای مستطیل بر هم عمود باشند، به آن مربع می‌گویند.

آیا قطرهای مستطیل منصف یکدیگرند ؟

بله. قطرهای مستطیل، یکدیگر را به دو قسمت مساوی تقسیم می‌کنند.

حالت هم نهشتی برای اثبات منصف بودن قطرهای مستطیل چیست؟

بر اساس حالت هم نهشتی دو ضلع و زاویه بین یا (ض ز ض)، قطرهای مستطیل همدیگر را نصف می‌کنند.

آیا قطرهای مستطیل عمود منصف یکدیگرند ؟

خیر. از آنجایی که زاویه بین قطرهای مستطیل، برابر با 90 درجه نیست، قطرهای مستطیل فقط منصف یکدیگرند و بر هم عمود نیستند.

آیا قطرهای مستطیل نیمساز هستند ؟

خیر.

آیا قطرهای مستطیل محور تقارن آن هستند ؟

خیر. اگر یک مستطیل را از روی قطر آن تا کنیم، دو طرف مستطیل بر روی یکدیگر منطبق نمی‌شوند.

روش محاسبه قطر مستطیل چیست ؟

روش اصلی محاسبه قطر مستطیل، استفاده از قضیه فیثاغورس است.