شعاع چیست؟ — شعاع دایره به زبان ساده (+ فیلم آموزش رایگان)

در آموزش‌های قبلی مجله فرادرس، با برخی شکل‌های هندسی مانند مستطیل، مثلث، مربع، لوزی، بیضی و دایره آشنا شدیم. در این آموزش، می‌خواهیم با یکی از مشخصات مهم دایره، یعنی شعاع دایره آشنا شویم. پیش از مطالعه این مطلب و برای آشنایی بیشتر با دایره، پیشنهاد می‌کنیم به آموزش «دایره چیست؟ — تعریف و مفاهیم به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.

فیلم آموزش شعاع چیست؟ — شعاع دایره به زبان ساده (+ فیلم آموزش رایگان)

دایره چیست؟

دایره مجموعه‌ای از نقاط روی یک صفحه دو بعدی است که فاصله یکسانی از نقطه‌ای به نام مرکز دارند.

این فاصله نقاط از مرکز دایره، شعاع نامیده می‌شود. اندازه دایره با تغییر طول شعاع تغییر می‌کند.

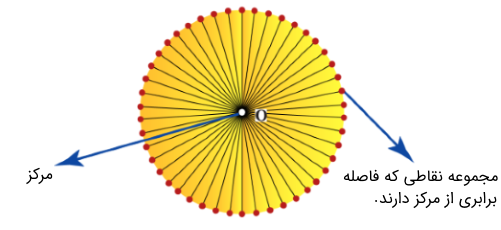
شعاع چیست ؟

تعریف دقیق شعاع دایره، طول یک پاره‌خط از مرکز دایره تا نقطه‌ای روی محیط یا همان مرز آن است. شعاع را معمولاً با $$r$$ نمایش می‌دهند که حرف اول معادل انگلیسی شعاع، یعنی Radius است.

به شکل زیر توجه کنید:

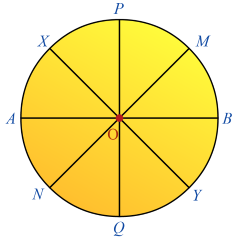
نقاط $$ A $$، $$B$$، $$M$$، $$N$$، $$P$$، $$Q$$، $$X$$ و $$Y$$ روی مرز دایره قرار داشته و فاصله یکسانی از مرکز $$O$$ دارند:

$$ \large OA=OB=OM=ON=OP=OQ=OX=OY $$

برای آشنایی بیشتر با اشکال مختلف هندسی، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه فیلم‌های آموزش دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.

شعاع دایره و قطر دایره

قطر بزرگ‌ترین وتر دایره است. وتر پاره‌خطی است که دو نقطه روی محیط دایره را به هم وصل می‌کند. در واقع، می‌توان چنین گفت که قطر پاره‌خطی است که دو نقطه دایره را به هم وصل می‌کند و از مرکز دایره نیز عبور می‌کند. از تعریف شعاع دایره می‌توان برای درک قطر دایره استفاده کرد.

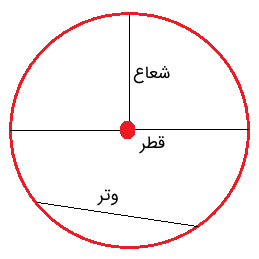
قطر دو برابر شعاع است. قطر را معمولاً با $$ D $$ نشان می‌دهیم که حرف اول معادل انگلیسی آن، یعنی Diameter است.

$$ D = 2  r $$

شعاع و محیط دایره

محیط دایره همان مرز دایره است و آن را با $$ C $$ که ابتدای معادل انگلیسی Circumference است، نشان می‌دهند. فرمول محیط دایره به صورت زیر بیان می‌شود:

$$ \large C = 2\pi r $$

که در آن، $$ C $$ محیط دایره، $$ r $$ شعاع دایره و $$ \pi $$ عدد ثابت و اندازه تقریبی آن $$ 3.14 $$ است.

برای آشنایی بیشتر با محیط دایره، به مطلب «محیط دایره — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید. همچنین، برای آشنایی با عدد پی، توصیه می‌کنیم مطلب «عدد پی (Π) و کاربردهای آن — به زبان ساده» را مطالعه کنید.

شعاع و مساحت دایره

مساحت دایره فضایی است که دایره در بر می‌گیرد. مساحت را معمولاً با $$A$$ که حرف اول کلمه Area است نشان می‌دهند و برابر است با:

$$A= \large \pi r ^ 2 $$

که در آن، $$ r $$ شعاع دایره و $$ \pi $$ همان عدد پی و مقدار تقریبی‌اش $$ 3. 14 $$ است.

برای آشنایی بیشتر با مساحت دایره، پیشنهاد می‌کنیم به مطلب «مساحت دایره — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.

فرمول‌های شعاع دایره

شعاع دایره را می‌توان با داشتن قطر، محیط یا مساحت دایره به دست آورد. با توجه به فرمول‌هایی که در بالا گفتیم، این کار امکان‌پذیر است.

شعاع دایره برحسب قطر ($$ D $$) دایره به صورت زیر به دست می‌آید:

$$ \large \boxed {r = \frac D 2 }$$

شعاع دایره برحسب محیط ($$C$$) دایره به صورت زیر به دست می‌آید:

$$ \large \boxed{r = \frac { C } { 2 \pi}} $$

شعاع دایره از مساحت دایره به صورت زیر محاسبه می‌شود:

$$ \large \boxed{r = \sqrt { \small {A}/{\pi}}}$$

شعاع یک قطعه

قسمت زرد شکل زیر، یک قطعه از دایره را نشان می‌دهد. شعاع این قطعه، شعاع دایره‌ای است که این قطعه بخشی از آن دایره است.

فرمول یافتن شعاع، وقتی وتر قاعده قطعه ($$ w $$) و ارتفاع ($$H$$) عمود بر وتر را در نقطه میانی قاعده کمان داریم، به صورت زیر خواهد بود:

$$ \large \text{r}= \frac{\text{H}}{2} +\frac{\text{W}^2}{8\text{H}} $$

مثال‌های شعاع دایره

در این بخش، چند مثال را از شعاع دایره حل می‌کنیم.

مثال اول شعاع دایره

مساحت دایره‌ای برابر با $$ 12.56\: \text{cm}^2 $$ است. قطر این دایره را به دست آورید ($$ \pi = 3.14$$).

حل: از فرمول مساحت دایره استفاده کرده و شعاع را به دست می‌آوریم:

$$ \large \begin {align}
A &= \pi r ^ 2 \\
\therefore 12.56 & = ( \pi \times r ^ 2 ) \\
12.56 & = \text {r} ^ 2 \times 3.14 \\
r ^ 2 & = \frac {12.56} {3.14} \\
r & = \sqrt { \frac {12.56} {3.14} } \\
r & = \sqrt { 4 } \\
r & = 2 \: \text {cm}
\end {align} $$

اکنون که اندازه شعاع را می‌دانیم، می‌توانیم قطر دایره را محاسبه کنیم:

$$ \large \begin{align} D & = 2 r \\
& = 2 \times 2 \\
& = 4 \: \text {cm}
\end {align} $$

مثال دوم شعاع دایره

قطر دایره‌ای برابر با $$ D = 55 \; \text{cm}$$ است. اندازه شعاع این دایره چقدر است؟

حل: همان‌طور که می‌دانیم، اندازه شعاع یک دایره، نصف اندازه قطر آن است. بنابراین، شعاع برابر است با:

$$ \large r = \frac D 2 = \frac {55}{2} = 27.5 \; \text{cm}$$

مثال سوم شعاع دایره

با توجه به شکل زیر، شعاع منحنی را محاسبه کنید.

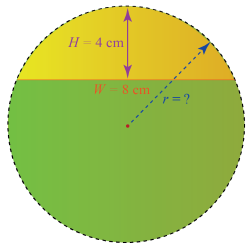
حل: شعاع منحنی به صورت زیر محاسبه می‌شود:

$$ \large r = \frac { \text {H}} { 2 } +\frac { \text {W} ^ 2 }{ 8 \text {H}} $$

با توجه به شکل، مقادیر زیر را داریم:

$$ \large \begin{align}
\text{W} &= 8\\
\text{H}&=4
\end{align} $$

با جایگذاری این مقادیر در فرمول، خواهیم داشت:

$$ \large \begin {align}
r & = \frac { { 4 } } { 2 } + \frac { 8 ^ 2 } { 8 \times \text {4} } \\
& = 2 + \frac { 6 4 } { 3 2 } \\
& = 2 + 2 \\
& = 4 \end {align} $$

معرفی فیلم آموزش هندسه پایه دهم (هندسه ۱) فرادرس

برای آشنایی بیشتر با مباحث اشکال هندسی، پیشنهاد می‌کنیم به فیلم آموزش هندسه پایه دهم (هندسه ۱) مراجعه کنید که توسط فرادرس تهیه شده است. این آموزش ویدیویی که مدت زمان آن ۴ ساعت و ۳ دقیقه است، شامل چهار درس می‌شود.

در درس اول این آموزش، موضوعات ترسیم‌های هندسی و استدلال بیان شده‌اند. مباحث درس دوم، به قضیه تالس و تشابه مثلث‌ها و کاربردهای آن‌ها اختصاص یافته است. در درس سوم، مباحث مربوط به چندضلعی‌ها و ویژگی‌هایی از آن‌ها و همچنین، مساحت و کاربردهای آن مورد بیان شده است. در نهایت، موضوع درس چهارم، تجسم فضایی است که خط، نقطه و صفحه و همچنین تفکر تجسمی را شامل می‌شود.

• برای مشاهده فیلم آموزش هندسه پایه دهم (هندسه ۱) + اینجا کلیک کنید.

برای یادگیری اشکال مختلف هندسی و محاسبه محیط، مساحت و حجم آن‌ها، توصیه می‌کنیم آموزش‌های مجله فرادرس را که در این زمینه تهیه شده‌اند، مطالعه کنید:

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس دبیرستان و پیش‌دانشگاهی
• آموزش هندسه پایه دهم (هندسه ۱)
• مجموعه آموزش‌های دروس ریاضیات
• آموزش فیزیک پایه یازدهم
• اعداد با توان کسری | به زبان ساده
• فرمول های محیط و مساحت اشکال هندسی (+ فیلم و PDF رایگان)
• محاسبه درصد آزمون | درصد گیری در کنکور و تست — به زبان ساده

بر اساس رای 7 نفر

آیا این مطلب برای شما مفید بود؟