تقارن محوری چیست؟ — به زبان ساده + مثال و فیلم آموزشی

اگر بتوان شکل یا جسمی را به دو یا چند قسمت مساوی تقسیم کرد، بهطوری که بخشی از یک تصویر سازمانیافته را بسازند، میگوییم با هم تقارن دارند. در این آموزش از مجله فرادرس، با یکی از انواع تقارن در هندسه، یعنی تقارن محوری آشنا میشویم. برای آشنایی با تقارن مرکزی، به آموزش «تقارن مرکزی چیست؟ — به زبان ساده + مثال و فیلم آموزشی» مراجعه کنید.
فیلم آموزشی تقارن محوری
تقارن چیست؟
اگر به فرهنگ لغت عمید مراجعه کنیم، میبینیم که برای واژه تقارن که در اصل کلمهای عربی است، این معانی آمده است: «قرینه بودن و تطابق دو شکل در دو سوی یک نقطه.» اما، در ریاضی و هندسه، وقتی از تقارن نام میبریم، منظور این است که وقتی یک شکل جابهجا، چرخانده یا بازتاب شود، مشابه شکل دیگر خواهد شد. همین موضوع را میتوان برای دو بخش از یک شکل واحد نیز بیان کرد. در ریاضیات و هندسه مدرسه، بیشتر بر تقارن دو بخش یک شکل تأکید میشود. بنابراین، ما نیز در این آموزش بر همین موضوع تمرکز میکنیم. در واقع، شکلی متقارن است که بتوان آن را به دو بخش مشابه تقسیم کرد.
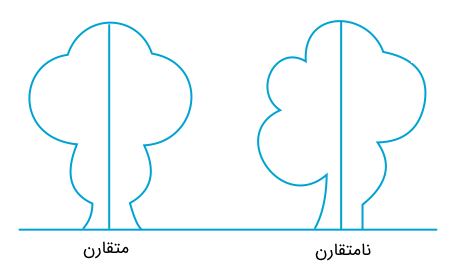
تقارن را بهراحتی میتوان با چشم تشخیص داد. برای مثال، شکل بالا نمونهای از یک شکل متقارن و یک شکل نامتقارن را نشان میدهد.
تقارن محوری چیست؟
تقارن محوری یکی از انواع تقارن است که نمونههای آن در اطرافمان بهوفور یافت میشود. وقتی شکلی نسبت به یک خط (یا محور) متقارن باشد، میگوییم تقارن نوع محوری دارد. شکل سمت چپ تصویر بخش قبل یک تقارن نوع محوری را نشان میدهد.
با یک مثال، تقارن محوری را بیشتر توضیح میدهیم. شکل زیر را در نظر بگیرید.
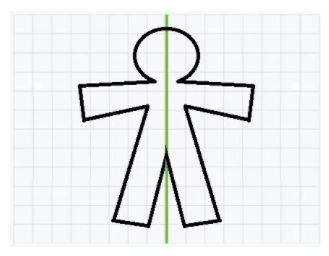
از میان سه عمل جابهجایی، چرخش و بازتاب، تقارن نوع محوری با عمل «بازتاب» تعریف میشود. برای وجود تقارن نوع محوری، باید خطی وجود داشته باشد بازتاب بخشی از شکل نسبت به آن، بخش دیگرش را بسازد. اما بازتاب چیست؟ عمل بازتاب را میتوان با یک تصور ساده درک کرد. برای مثال، آدمک شکل بالا را در نظر بگیرید. فرض کنید این آدمک را روی کاغذ رسم میکنیم. اگر کاغذ را دقیقاً روی خط سبز نشاندادهشده در شکل تا کنیم، میبینیم که دو نیمه آن دقیقاً بر هم منطبق خواهند شد. این همان مفهموم بازتاب است.

بنابراین، برای آنکه بفهمیم شکلی تقارن از نوع محوری دارد یا نه، کافی است ببینیم که آیا میتوان خطی پیدا کرد که با تا کردن شکل روی آن، دو بخش کاملاً بر هم نطبق شوند یا نه.
در ادامه، با محور تقارن آشنا میشویم.
برای آشنایی با مباحث ریاضیات مدرسه، پیشنهاد میکنیم به مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
خط تقارن محوری یا محور تقارن چیست؟
خطی که شکل را به دو قسمت مساوی تقسیم میکند یا برش میدهد، بهگونهای که تقارن محوری بهوجود بیتید، «محور تقارن» نامیده میشود. محور تقارن را «خط تقارن» یا «خط تقارن محوری» نیز مینامند. میتوان گفت که محور تقارن اشکال را به دو قسمت تقسیم میکند که بازتاب یکدیگر هستند. شکل زیر محور تقارن یک تصویر متقارن را نشان میدهد.
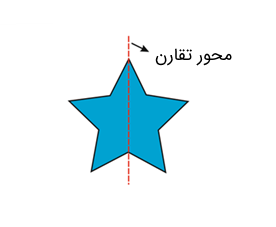
انواع محور تقارن
محور تقارن را میتوان بر اساس قرارگیریاش به سه نوع اصلی تقسیم کرد:
- خط افقی تقارن
- خط عمودی تقارن
- خط مایل یا مورب تقارن
محورهای تقارن در اشکال هندسی مختلف در شکل زیر نشان داده شده است.
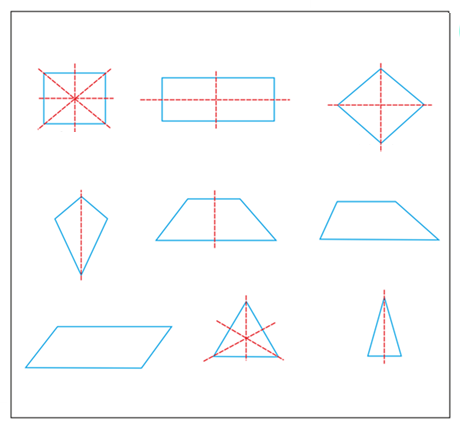
محور افقی تقارن
وقتی شکلی را به صورت افقی، یعنی از چپ به راست یا راست به چپ، تقسیم کنیم یا برش دهیم و بازتاب قسمتهای تشکیل شده یکسان باشند، گفته میشود که آنها تقارن نوع محوری دارند و محور تقارن را افقی مینامیم.
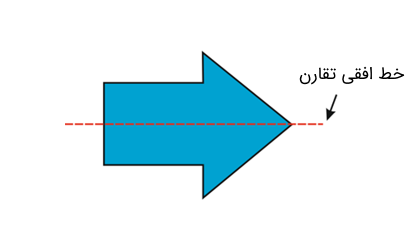
اگر شکل زیر را روی کاغذ رسم کنیم، سپس به صورت افقی از چپ به راست برش دهیم، خواهیم دید که اگر کاغذ را از خط تقارن تا کنیم، قسمتهای بالا و پایین خط تقارن روی هم قرار میگیرند و یکسان هستند. بنابراین خط تقارن به خط افقی تقارن معروف است.
محور عمودی تقارن
خط عمودی تقارن اشکال یا تصاویر را به دو قسمت یکسان در سمت چپ و راست تقسیم میکند یا برش میدهد و بازتاب میدهد. خود خط از بالا به پایین رسم میشود.
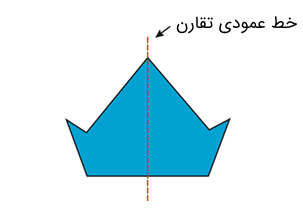
برای مثال، شکل زیر را به صورت عمودی به سمت پایین برش دادهایم. وقتی خط تقارن عمودی است، شکلها در سمت چپ و راست خط تقارن به دو بخش یکسان تقسیم میشوند. بنابراین، خط تقارن به عنوان خط عمودی تقارن شناخته میشود.
محور مورب تقارن
وقتی شکلی را در امتداد یک خط مورب به دو قسمت یکسان تقسیم کنیم یا برش دهیم و دو بخش بازتاب یکدیگر باشند، خط تقارن را خط تقارن مورب میگویند. خط مورب تقارن شکل را به صورت مورب قطع میکند.
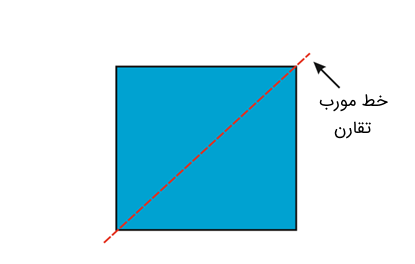
برای مثال، هنگامی که شکل زیر به صورت مورب بریده میشود، هر دو قسمت از دو طرف مورب (خط تقارن) بازتاب هم هستند.
تقارن محوری و قرینه یک نقطه نسبت به یک خط
دقت کنید که تقارن نوع محوری محدود به شکلها نمیشود، بلکه برای نقطه یا نقاط مختلف نیز بیان میشود. در واقع، اگر نقطه یا نقاطی، چه بهصورت منفرد و چه بهعنوان بخشی از یک شکل داشته باشیم نیز میتوان تقارن محوری را بررسی کرد.
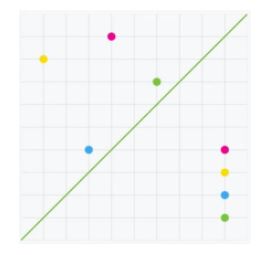
تصویر زیر مثال خوبی برای بررسی تقارن است. به خط تقارن سبز دقت کنید که مورب است. اگر به دو سمت این خط دقت کنیم، میبینیم که تنها نقطههای آبی متقارن هستند و تقارن نوع محوری دارند. برای درک بهتر، به فاصله نقاط دو طرف از محور تقارن دقت کنید.
شکل هایی با یک تقارن محوری
برخی از شکلها فقط یک محور تقارن دارند. خط تقارن این شکلها را به دو قسمت مساوی تقسیم میکند. یک خط تقارن ممکن است عمودی، افقی یا مورب باشد.
برای مثال، حرف انگلیسی A فقط یک خط تقارن دارد. این خط تقارن عمودی است.

شکل هایی با دو تقارن محوری
بعضی از شکلها بهگونهای هستند که میتوان برای آنها دو محور تقارن مختلف رسم کرد. این محورها میتوانند یکی از سه نوع عمودی، افقی و قطری یا همان مورب باشند.
برای مثال، برای حرف انگلیسی X میتوان دو محور تقارن افقی و عمودی رسم کرد.
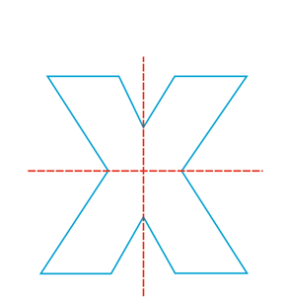
شکل هایی با سه تقارن محوری
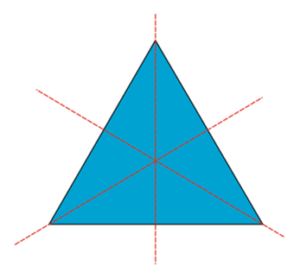
شکلهایی نیز وجود دارند که سه محور تقارن دارند. برای مثال، مثلث متساویالاضلع شکل زیر از هر سه نوع عمودی و افقی و مورب یک محور تقارن دارد.
شکل هایی با چهار تقارن محوری
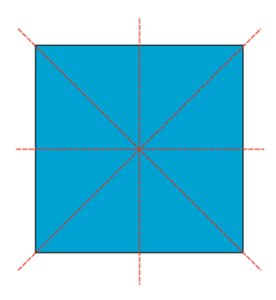
اما شکلهایی با چهار محور تقارن و بیشتر از آن نیز وجود دارند. برای مثال، مربع شکل زیر چهار محور تقارن دارد که یکی از آنها عمودی، یکی افقی و دوتایشان مورب است.
شکل هایی با بیش از چهار تقارن محوری
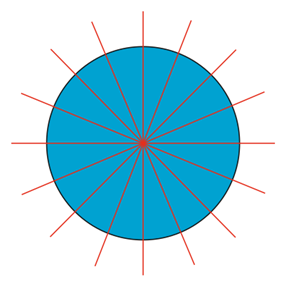
شکلهایی نیز وجود دارند که میتوان برای آنها محورهای تقارن بیشتری رسم کرد. برای مثال، دایره یکی از شکلهایی است که بینهایت محور تقارن دارد.
مثال های تقارن محوری
در این بخش، چند مثال را از تقارن محوری بررسی میکنیم.
مثال اول تقارن محوری
شکل زیر چند محور تقارن دارد؟ نوع آن را مشخص کنید.

جواب: همانطور که میبینیم، برای این شکل نمیتوان بیش از یک محور تقارن رسم کرد که این محور عمودی است.

مثال دوم تقارن محوری
در یک مثلث متساویالاضلاع چند خط تقارن وجود دارد؟ آنها را رسم کنید.
جواب: مثلث متساویالاضلاع مثلثی است که سه ضلع آن برابر باشد. خطی که از رأس به سمت ضلع مقابل مثلث کشیده شده است، آن را به دو نیمه مساوی تقسیم میکند. بنابراین، میانه یا ارتفاع مثلث متساویالاضلاع، خط تقارن است که شکل را بهصورت تصاویر آینهای یا بازتابی برش میدهد.

سه رأس در مثلث متساویالاضلاع وجود دارد. بنابراین، مجموع خطوط تقارن در مثلث متساویالاضلاع 3 است.
مثال سوم تقارن محوری
تصویر زیر تاج محل هند را نشان میدهد. آیا خط رسمشده یک محور تقارن بازتابی است؟

جواب: میدانیم که در تقارن بازتابی، نیمی از جسم یا شکل، نیمی دیگر را منعکس میکند و اگر آن رو روی کاغذ چاپ کنیم، باید با تا کردن از محل محور تقارن، این دو شکل روی هم بیفتند. در اینجا، خط قرمز تصویر تاج محل را به دو نیمه مساوی تقسیم میکند و هر نیمه تصویر آینهای است.
بنابراین، تقارن نشان داده شده در تصویر تاج محل، تقارن بازتابی است.
مثال چهارم تقارن محوری
مشخص کنید که کدامیک از تصاویر زیر متقارن هستند.
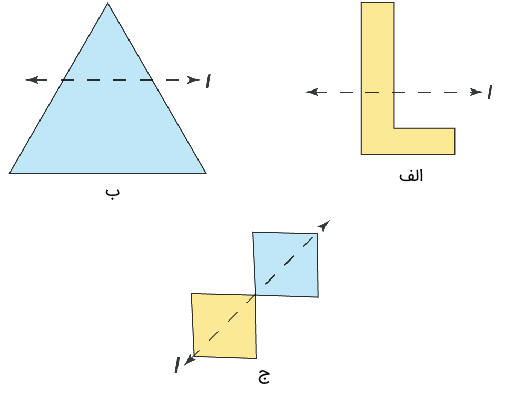
جواب: همانطور که میدانیم، زمانی که بتوان یک شکل را حول محور به دو قسمت تقسیم کرد که بازتاب داشته باشند، آن محور محور تقارن است. از شکلهای دادهشده در بالا، تنها شکل (ج) دارای تقارن است.
مثال پنجم تقارن محوری
شکل زیر داده شده است. شکلی رسم کنید که با این شکل تقارن نوع محوری داشته باشد. محور تقارن مشخص شده است.

جواب: کافی است نقاطی را روی محیط شکل مشخص و بارتاب آنها را نسبت به محور عمودی رسم کنیم. در نهایت، شکل سمت راست ایجاد میشود که میتوانیم آن را رنگآمیزی کنیم.
مثال ششم تقارن محوری
همانطور که در شکل زیر مشخص است، دو محور تقارن وجود دارد و یک شکل رسم شده است. شکلهایی رسم کنید که نسبت به محورهای رسمشده با شکل اصلی تقارن داشته باشند.
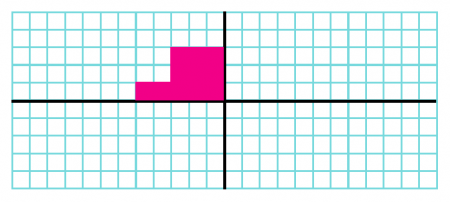
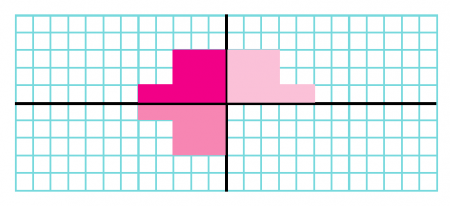
جواب: دو شکل رسم میکنیم که نسبت به شکل اصلی تقارن عمودی و افقی داشته باشند.
مثال هفتم تقارن محوری
به شکل زیر دقت کنید. آن را بهگونهای تکمیل کنید که نسبت به محور افقی داری تقارن نوع محوری باشد.
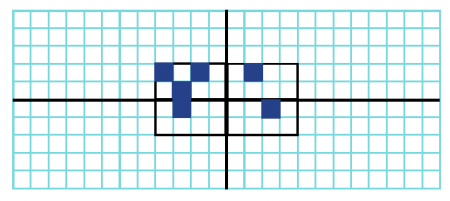
جواب: شکل زیر جواب این مثال است.
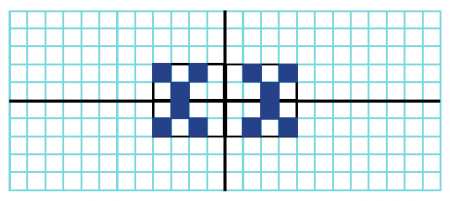
مثال هشتم تقارن محوری
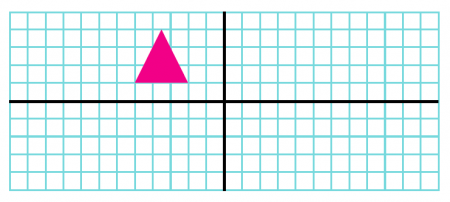
همانطور که در شکل زیر مشخص است، دو محور تقارن وجود دارد و یک مثلث رسم شده است. شکلهایی رسم کنید که نسبت به محورهای رسمشده با شکل اصلی تقارن داشته باشند.
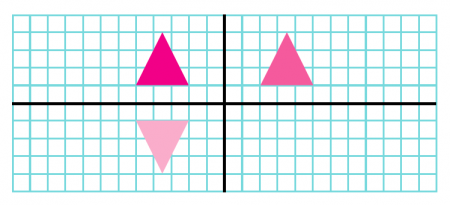
جواب: دو مثلث دارای تقارن با مثلث اصی در شکل زیر رسم شده اند.
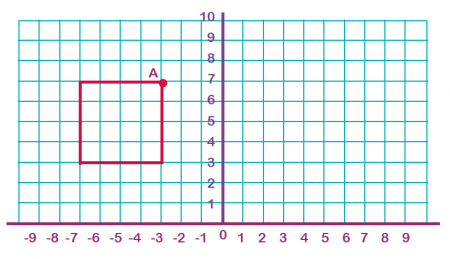
مثال نهم تقارن محوری
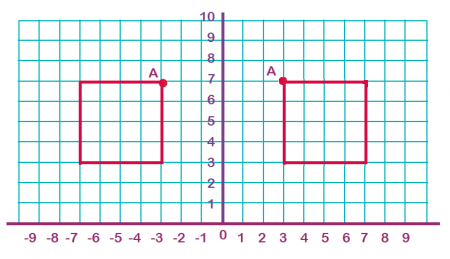
به شکل زیر دقت کنید. سعی کنید این شکل را با دقت روی کاغذ رسم کنید و مربع متقارن نسبت به مربع اصلی را نسبت به محور عمودی رسم کنید.
جواب: تصویر زیر جواب این مثال است.
جمعبندی
در این آموزش از مجله فرادرس، با تقارن نوع محوری آشنا شدیم و دیدیم که سه نوع تقارن محوری عمودی، افقی و مورب وجود دارد. همچنین، مثالهایی را از تقارن نوع محوری در برخی اشکال هندسی بیان کردیم.












