محاسبه قطر متوازی الاضلاع — فرمول های محاسبه + حل تمرین و مثال
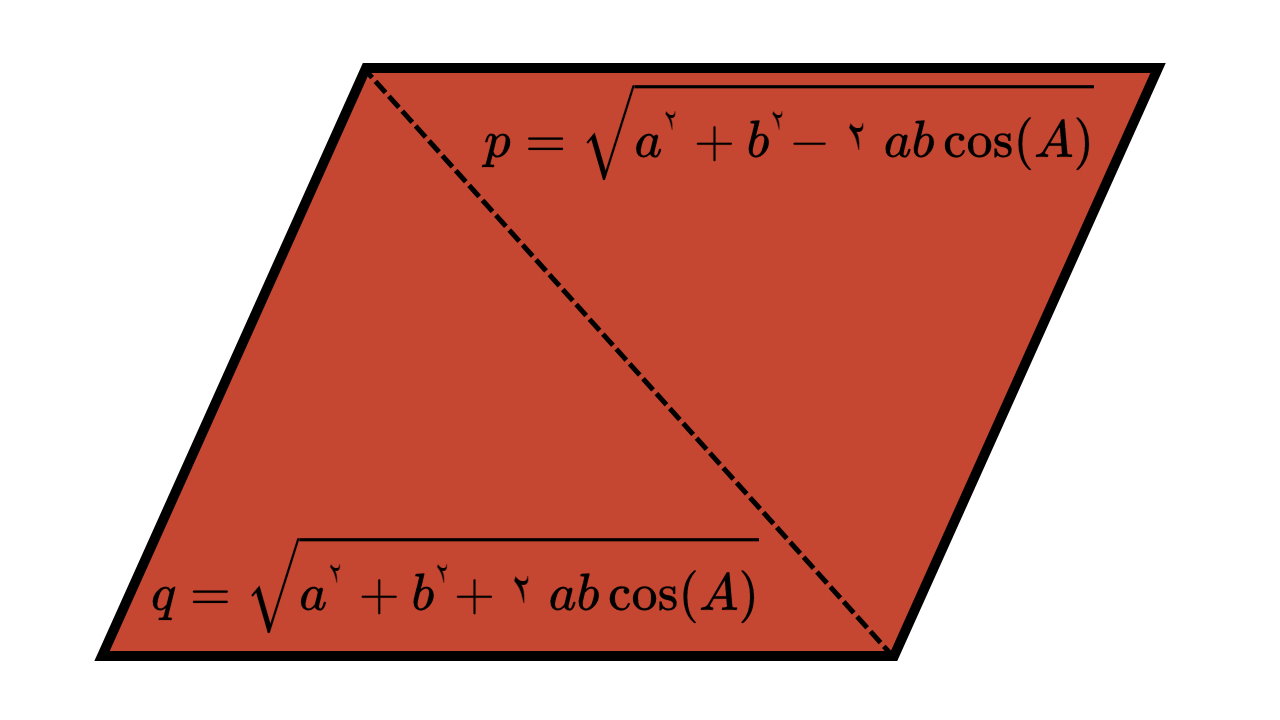
قطر متوازیالاضلاع، پارهخطی است که بین دو گوشه غیر مجاور این چهارضلعی رسم میشود. متوازیالاضلاع، دو قطر دارد. محاسبه اندازه این قطرها با توجه به اندازه ضلعها و زاویه بین آنها انجام میگیرد. در این آموزش، روشها و فرمولهای محاسبه قطر متوازی الاضلاع را به همراه حل چند مثال توضیح میدهیم.
قطر متوازی الاضلاع چیست و چگونه رسم میشود؟
قطر متوازیالاضلاع، فاصله بین راسهای مقابل آن است.
متوازیالاضلاع زیر را در نظر بگیرد.
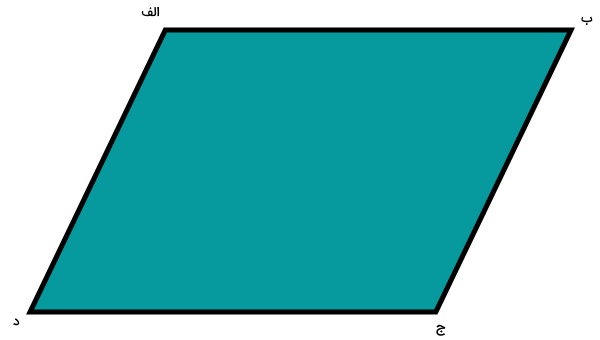
اگر دو راس روبهرویی مانند راسهای ب و د را توسط یک پارهخط به یکدیگر وصل کنیم، یکی از قطرهای متوازیالاضلاع رسم میشود.
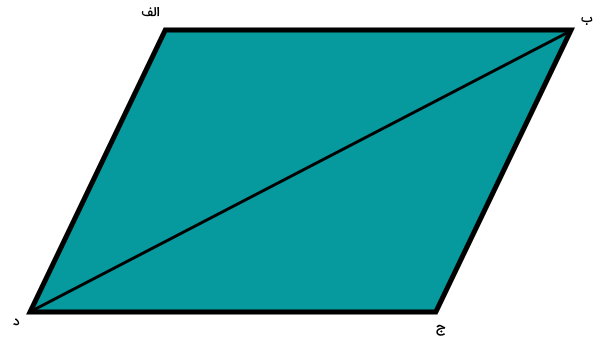
متوازیالاضلاع دو قطر دارد. قطرهای متوازیالاضلاع، همدیگر را نصف میکنند. به علاوه، با رسم هر قطر، متوازیالاضلاع به دو مثلث همنهشت تبدیل میشود.
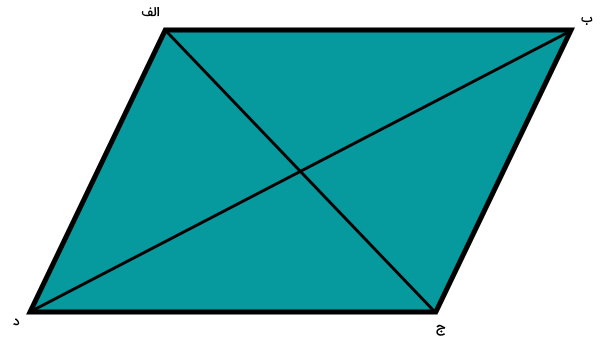
اندازه قطرها، معمولا به منظور محاسبه محیط و مساحت متوازیالاضلاع مورد استفاده قرار میگیرند.
فرمول مساحت متوازی الاضلاع با قطر
فرمول مساحت متوازیالاضلاع با قطر به صورت زیر نوشته میشود:
$$
S = \frac {۱}{۲} pq \sin {\alpha}
$$
- S: مساحت متوازیالاضلاع
- p: اندازه یکی از قطرها
- q: اندازه قطر دیگر
- α: اندازه زاویه بین دو قطر
در صورت نمایش برداری قطرها، فرمول بالا به شکل زیر در میآید:
$$
S = \frac {۱}{۲} \overrightarrow {p} \times \overrightarrow {q}
$$
فرمول محیط متوازی الاضلاع با قطر
محیط متوازیالاضلاع با قطر از فرمول زیر به دست میآید:
$$
P = ۲a +\sqrt{۲p^۲+۲q^۲-۴a^۲}
$$
رابطه بین قطر و ضلع متوازی الاضلاع
رابطه بین قطر و ضلع متوازی الاضلاع عبارت است از:
$$
p^{۲}+q^{۲}= ۲ (a^{۲}+ b^{۲})
$$
رابطه بالا، مبنای فرمولهای محاسبه قطر متوازی الاضلاع است.
محاسبه قطر متوازی الاضلاع چگونه انجام میشود؟
محاسبه قطر متوازی الاضلاع با استفاده از اندازه ضلعها و زاویه بین آنها انجام میگیرد.
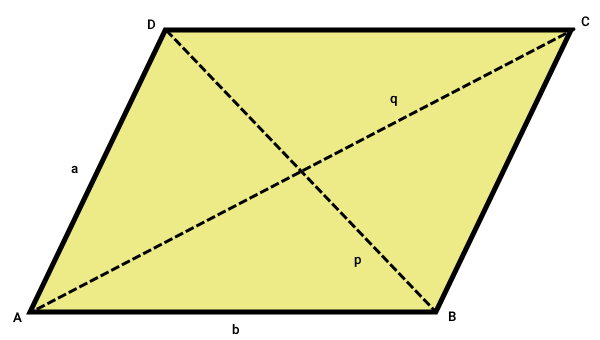
متوازیالاضلاع بالا را در نظر بگیرید. بر اساس اندازههای مشخص شده در این متوازیالاضلاع، فرمول محاسبه قطر متوازی الاضلاع به صورت زیر نوشته میشود:
$$
p=\sqrt{a^{۲}+b^{۲}-۲ a b \cos (A)}
$$
$$
= \sqrt{a^{۲}+b^{۲}+۲ a b \cos (B)}
$$
$$
q=\sqrt{a^{۲}+b^{۲}+۲ a b \cos (A)}
$$
$$
=\sqrt{a^{۲}+b^{۲}-۲ a b \cos (B)}
$$
فرمولهای بالا، با استفاده از قواعد مثلثات به دست میآیند. به تغییر علامت ضریب کسینوس در حالتهای مختلف دقت کنید. هنگام محاسبه قطر مقابل به زاویه مورد نظر، علامت ضریب کسینوس منفی خواهد بود.
مثال 1: محاسبه قطر متوازی الاضلاع با دو ضلع و زاویه بین
ضلعهای مجاور متوازیالاضلاعی برابر 3 و 5 سانتیمتر هستند. اگر زاویه بین این دو ضلع برابر 120 درجه باشد، اندازه قطر مقابل به زاویه معلوم چقدر است؟
بر اساس فرمول قطر متوازیالاضلاع، داریم:
$$
p=\sqrt{a^{2}+b^{2}-2 a b \cos (A)}
$$
- p: قطر متوازیالاضلاع
- a: یکی از ضلعها برابر 3 سانتیمتر
- b: ضلع دیگر برابر 5 سانتیمتر
- A: زاویه مقابل قطر p برابر 120 درجه
اندازههای معلوم را درون فرمول بالا قرار میدهیم:
$$
p=\sqrt{۳^{۲}+۵^{۲}-(۲\times ۳ \times ۵ \times \cos ۱۲۰^{\circ})}
$$
کسینوس زاویه 120 درجه برابر 0/5- است:
$$
p=\sqrt{۹+۲۵-(۳۰ \times (-۰/۵))}
$$
$$
p=\sqrt{۹+۲۵-(-۱۵)}
$$
$$
p=\sqrt{۹+۲۵+۱۵}
$$
$$
p=\sqrt{۴۹}
$$
$$
p=۷
$$
مثال 2: محاسبه قطر متوازی الاضلاع با دو ضلع و زاویه مجاور
طول q را حساب کنید.
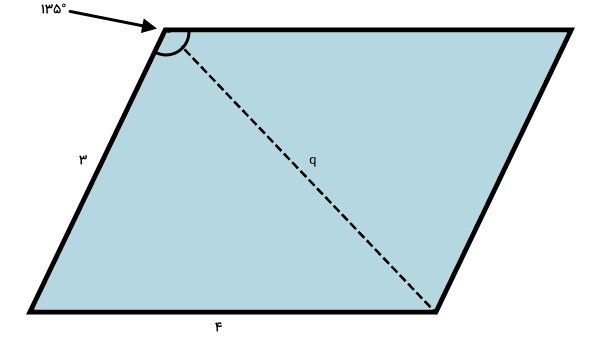
در متوازیالاضلاع بالا، اندازه دو ضلع و زاویه مجاور آنها داده شده است. صورت سوال، طول قطر مجاور زاویه معلوم را از ما میخواهد. برای به دست آوردن این اندازه، فرمول زیر را مینویسیم:
$$
q=\sqrt{a^{۲}+b^{۲}+۲ a b \cos (A)}
$$
- q: قطر متوازیالاضلاع
- a: یکی از ضلعها برابر 3
- b: ضلع دیگر برابر 4
- A: زاویه مجاور قطر q برابر 135 درجه
$$
q=\sqrt{۳^{۲}+۴^{۲}+ (۲ \times ۳ \times ۴ \times \cos ۱۳۵^{\circ})}
$$
کسینوس زاویه 135 درجه، حدودا برابر 0/71- است:
$$
q=\sqrt{۲۵+ (۲۴ \times (-۰/۷۱))}
$$
$$
q=\sqrt{۲۵-۱۷/۰۴}
$$
$$
q=\sqrt{۷/۹۶}
$$
$$
q=۲/۸۲
$$
طول q، برابر 2/82 است.
مثال 3: محاسبه قطر متوازی الاضلاع با دو ضلع و قطر دیگر
اندازه دو ضلع و یک قطر متوازیالاضلاعی به ترتیب برابر 6، 10 و 14 متر است. اندازه قطر دیگر را حساب کنید.
بین قطرها و ضلعهای یک متوازیالاضلاع، رابطه زیر برقرار است:
$$
p^{۲}+q^{۲}= ۲ (a^{۲}+ b^{۲})
$$
- p: اندازه یکی از قطرها برابر 14 متر
- q: اندازه قطر دیگر
- a: اندازه یکی از ضلعها برابر 6 متر
- b: اندازه ضلع دیگر برابر 10 متر
با قرار دادن اندازههای معلوم در رابطه بالا، اندازه قطر مجهول به دست میآید:
$$
۱۴^{۲}+q^{۲}= ۲ (۶^{۲}+ ۱۰^{۲})
$$
$$
۱۹۶+q^{۲}= ۲ (۳۶+ ۱۰۰)
$$
$$
۱۹۶+q^{۲}= ۲ (۱۳۶)
$$
$$
۱۹۶+q^{۲}= ۲۷۲
$$
$$
q^{۲}= ۲۷۲ - ۱۹۶
$$
$$
q^{۲}= ۷۶
$$
$$
q= \sqrt {۷۶}
$$
$$
q= ۸/۷۲
$$
در نتیجه، اندازه قطر مجهول برابر 8/72 متر است.
مثال 4: محاسبه قطر متوازی الاضلاع با مساحت
اندازه ضلعهای یک متوازیالاضلاع برابر ۱۲ و 8 میلیمتر است. اگر مساحت متوازیالاضلاع برابر ۴۸ میلیمتر مربع باشد، اندازههای قطرهای متوازیالاضلاع چقدر خواهد بود؟
برای حل این مسئله، باید با فرمول محاسبه مساحت متوازیالاضلاع با ضلع و زاویه آشنایی داشته باشید. بر اساس این فرمول، مساحت متوازیالاضلاع برابر است با:
$$
S = ab \sin {\alpha}
$$
- S: مساحت برابر ۴۸ میلیمتر مربع
- a: اندازه یکی از ضلعها برابر ۱۲ میلیمتر
- b: اندازه ضلع دیگر برابر 8 میلیمتر
- α: زاویه بین a و b
این فرمول به ما کمک میکند تا بتوانیم زاویه بین دو ضلع متوازیالاضلاع را به دست بیاوریم. به این منظور، اندازههای معلوم را درون فرمول قرار میدهیم:
$$
۴۸ = ۱۲ \times ۸ \times \sin {\alpha}
$$
$$
۴۸ = ۹۶ \times \sin {\alpha}
$$
$$
\sin {\alpha} = \frac {۴۸}{۹۶}
$$
$$
\sin {\alpha} = \frac {۱}{۲}
$$
$$
\sin {\alpha} = ۰/۵
$$
سینوس زاویه 30 درجه برابر 0/5 است. بنابراین، زاویه بین دو ضلع معلوم برابر 30 درجه است. اکنون تمام اندازههای مورد نیاز برای محاسبه قطر متوازی الاضلاع را داریم. یکی از قطرهای متوازیالاضلاع به کم فرمول زیر محاسبه میشود:
$$
p=\sqrt{a^{۲}+b^{۲}-۲ a b \cos (A)}
$$
- p: قطر متوازیالاضلاع
- a: یکی از ضلعها ۱۲ میلیمتر
- b: ضلع دیگر برابر ۸ میلیمتر
- A: زاویه مقابل قطر p برابر ۳۰ درجه
$$
p=\sqrt{۱۲^{۲}+۸^{۲}-(۲ \times ۱۲ \times ۸ \times \cos ۳۰^{\circ})}
$$
کسینوس زاویه 30 درجه، تقریبا برابر 0/87 است:
$$
p=\sqrt{۱۴۴+۶۴-(۲ \times ۱۲ \times ۸ \times ۰/۸۷)}
$$
$$
p=\sqrt{۲۰۸-(۱۹۲ \times ۰/۸۷)}
$$
$$
p=\sqrt{۲۰۸-۱۶۷/۰۴}
$$
$$
p=\sqrt{۴۰/۹۶}
$$
$$
p=۶/۴
$$
یکی از قطرهای متوازیالاضلاع برابر ۶/۴ میلیمتر است. برای محاسبه قطر اول، فرض کردیم این قطر در مقابل زاویه معلوم (30 درجه) قرار دارد. به همین دلیل، قطر دیگر، باید مجاور این زاویه باشد. بنابراین داریم:
$$
q=\sqrt{a^{۲}+b^{۲}+۲ a b \cos (A)}
$$
- q: قطر متوازیالاضلاع
- a: یکی از ضلعها برابر ۱۲
- b: ضلع دیگر برابر ۸
- A: زاویه مجاور قطر q برابر ۳۰ درجه
$$
q=\sqrt{۱۲^{۲}+۸^{۲}+ (۲ \times ۱۲ \times ۸ \times \cos ۳۰^{\circ})}
$$
$$
p=\sqrt{۲۰۸+۱۶۷/۰۴}
$$
$$
p=\sqrt{۳۷۵/۰۴}
$$
$$
p=۱۹/۳۷
$$
به این ترتیب، اندازه قطر دوم متوازیالاضلاع برابر 19/37 به دست آمد.
سوالات مرتبط با قطر متوازی الاضلاع و محاسبه آن
در این بخش به برخی از سوالات پرتکرار در رابطه با قطر متوازیالاضلاع و نحوه محاسبه آن پاسخ میدهیم.
تعریف قطر متوازی الاضلاع چیست؟
قطر متوازیالاضلاع، پارهخطی اتصالدهنده گوشههای روبهرویی متوازیالاضلاع است.
طول قطر متوازیالاضلاع چگونه محاسبه میشود؟
قطر متوازیالاضلاع با استفاده از اندازه دو ضلع و یکی از زاویههای متوازیالاضلاع محاسبه میشود.
آیا قطر متوازی الاضلاع نیمساز است ؟
خیر. قطرهای متوازیالاضلاع، مگر در حالتهای خاص (مربع و لوزی)، نیمساز زاویه راسها نیستند.
آیا قطرهای متوازی الاضلاع با هم برابرند ؟
خیر. فقط قطرهای مربع (یکی از انواع متوازیالاضلاع) با هم برابرند.
آیا قطرهای متوازی الاضلاع منصف هستند ؟
بله. قطرهای متوازیالاضلاع، یکدیگر را به دو قسمت مساوی تقسیم میکنند.
آیا قطرهای متوازی الاضلاع بر هم عمودند ؟
خیر. فقط قطرهای لوزی و مربع (دو حالت خاص از متوازیالاضلاع) بر هم عمودند.
آیا در متوازی الاضلاع قطر ها عمود منصف یکدیگرند ؟
خیر. قطرهای متوازیالاضلاع، فقط منصف یکدیگرند و بر هم عمود نیستند.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت متوازی الاضلاع — هر آنچه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- متوازی الاضلاع چیست ؟ — تعریف و مفاهیم به زبان ساده
- محیط متوازی الاضلاع چیست ؟ — به زبان ساده + حل تمرین و مثال
- فرمول محیط متوازی الاضلاع چیست ؟ — معرفی انواع فرمول ها + حل مثال
- مساحت متوازی الاضلاع چیست ؟ — فیلم آموزش رایگان + حل تمرین و مثال
- محاسبه قطر متوازی الاضلاع — فرمول های محاسبه + حل تمرین و مثال(همین مطلب)
- محیط متوازی الاضلاع به صورت جبری — فرمول های ریاضی + حل مثال
- فرمول مساحت متوازی الاضلاع چیست ؟ — تمامی فرمول ها + حل تمرین و مثال
- مساحت متوازی الاضلاع به صورت جبری — انواع فرمول ها + حل مثال
- نمونه سوال مساحت متوازی الاضلاع با جواب — حل تمرین های متنوع
- مساحت متوازی الاضلاع با قطر چگونه بدست می آید ؟ + حل مثال
- مساحت متوازی الاضلاع با سینوس — به زبان ساده + حل مثال










