محیط چیست؟ — به زبان ساده + حل مثال های تصویری

محیط، مسافت دور شکلهای هندسی بسته است. محیط در کنار مساحت و حجم، از کمیتهای مهم در دنیای هندسه به شمار میروند. اندازه دور شکل، معمولا برای شکلهای دوبعدی نظیر دایره، مثلث، مربع و غیره تعریف میشود. با این وجود، شکلهای سهبعدی نظیر چندوجهیها نیز دارای محیط هستند. در این مقاله، روشهای محاسبه محیط انواع شکلهای هندسی دوبعدی و سهبعدی را به همراه حل مثال آموزش داده و به سوال «محیط چیست ؟» پاسخ میدهیم.
محیط چیست؟
اندازه دور هر شکل، با عنوان محیط آن شکل شناخته میشود.
در تصویر متحرک زیر، خط سیاه بر روی محیط یک دایره حرکت میکند. مسافت طی شده توسط خط سیاه، اندازه محیط دایره است.

تصویر زیر، یک شکل نامنظم را نمایش میدهد. مفهوم محیط در این شکل، هیچ تفاوتی با مفهوم محیط در دایره ندارد. در اینجا نیز، اندازه دور شکل، محیط آن است.
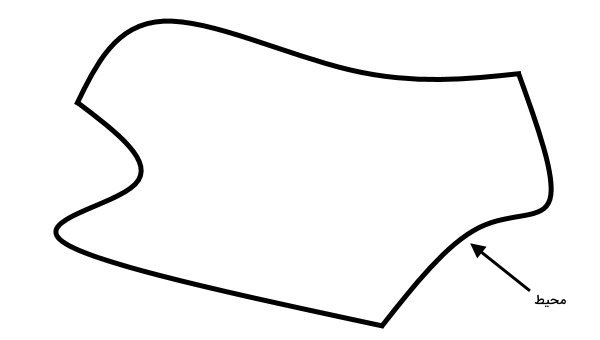
محیط چه کاربردی دارد ؟
محیط، از مفاهیمی است که کاربرد آن در زندگی روزمره هر کسی احساس میشود. در ریاضیات، این کمیت به منظور نمایش اندازه دور شکلهای هندسی مورد استفاده قرار میگیرد. در جغرافیا، محیط، مرزهای اطراف یک منطقه یا حتی یک کشور را نشان میدهد.

تعیین طول فنس مورد نیاز برای حصارکشی، محاسبه مسافت دور محدودههای زمین، نقشهبرداری و مسیریابی، از جمله کاربردهای محیط در زندگی روزمره هستند. در کنار این موارد، محیط، از پارامترهای مورد استفاده برابر تعیین حجم اجسام سهبعدی نیز محسوب میشود.
مثال ۱: محاسبه محیط یک چندضلعی
تصویر زیر، شکل یک چندضلعی و اندازه هر یک از ضلعهای آن را نمایش میدهد. محیط چندضلعی را به دست بیاورید.
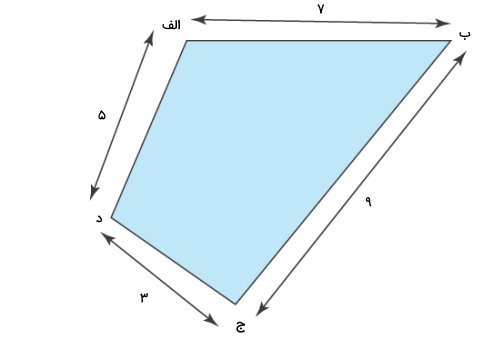
بر اساس تعریف، محیط یک شکل بسته، مسافت دور آن است. چندضلعی بالا، چهار ضلع به اندازههای ۵، ۷، ۹ و ۳ دارد. خود را بر روی گوشه (الف) در نظر بگیرید. با حرکت از روی گوشه (الف) تا گوشه (ب)، مسافت ۷ واحد را طی میکنید. از گوشه (ب) تا گوشه (ج)، به اندازه ۹ واحد، از گوشه (ج) تا گوشه (د)، به اندازه ۳ واحد و از گوشه (د) تا گوشه (الف)، به اندازه ۵ واحد به مسافت طی شده اضافه میشود.
هنگامی که دوباره به نقطه شروع (گوشه الف) میرسید، در واقع به اندازه محیط شکل جابجا شدهاید. مسافت طی شده در این مسیر برابر است با:
د تا الف + ج تا د + ب تا ج + الف تا ب = مسافت دور چندضلعی
به جای هر یک از مسیرها، اندازه آنها را قرار میدهیم:
۵ + ۳ + ۹ + ۷ = مسافت دور چندضلعی
۲۴ = مسافت دور چندضلعی
بنابراین، مسافت دور چندضلعی برابر با ۲۴ واحد است.
یکای محیط چیست ؟
محیط، دارای واحد طول است. به عنوان مثال، اگر مرزهای خاکی و آبی اطراف یک کشور را به عنوان محیط آن در نظر بگیریم، محیط ایران برابر با ۵۸۹۴ کیلومتر یا ۳۶۶۲ مایل خواهد بود. در کشور ما، محیط، بر اساس سیستم یکاهای بینالمللی (SI) بیان میشود. جدول زیر، رایجترین واحدهای بیان محیط را نمایش میدهد.
| یکای بیان محیط در سیستم SI | نماد یکای محیط |
| میلیمتر | mm |
| سانتیمتر | cm |
| متر | m |
| دکامتر | dam |
| هکتومتر | hm |
| کیلومتر | km |
سیستم یکاهای آمریکایی، از واحدهایی نظیر اینچ، فوت، یارد و مایل برای بیان محیط استفاده میکند. برای آشنایی با نحوه تبدیل این یکاها به یکاهای بینالمللی، مطالعه مطلب «تبدیل واحد | تمام فرمولها | راهنمای کامل و سریع» را به شما پیشنهاد میکنیم.
نماد محیط چیست ؟
در عبارتهای جبری، محیط چندضلعیها (مثلث، مربع و غیره) را با حرف انگلیسی P (ابتدای کلمه Perimeter) و محیط منحنیهای بسته (دایره، بیضی و غیره) را با حرف انگلیسی C (ابتدای کلمه Circumference) نمایش میدهند.
جدول محیط تمام شکل های هندسی
محیط تمام شکلهای هندسی شناختهشده را در قالب جدول زیر آوردهایم.
| شکل هندسی | فرمول محیط | توضیحات |
| مثلث |
a: اندازه ضلع اول b: اندازه ضلع دوم c: اندازه ضلع سوم | |
|
a: اندازه ضلع اول b: اندازه ضلع دوم γ: زاویه بین a و b | ||
|
γ: زاویه اول β: زاویه دوم a: ضلع بین γ و β | ||
| مثلث متساویالاضلاع |
a: اندازه یک ضلع | |
| مثلث متساویالساقین |
l: اندازه ساق b: اندازه قاعده | |
| مثلث قائمالزاویه |
a: اندازه یکی از ساقها b: اندازه ساق دیگر c: اندازه وتر | |
| مربع |
a: ضلع مربع | |
|
d: قطر مربع | ||
| مستطیل |
l: طول مستطیل w: عرض مستطیل | |
| دایره |
d: قطر دایره | |
|
r: شعاع دایره | ||
| نیمدایره |
r: شعاع دایره | |
|
d: قطر دایره | ||
| قطاع دایره |
r: شعاع دایره l: طول کمان | |
| ذوزنقه |
a: اندازه یکی از قاعدهها b: اندازه یکی از ساقها c: اندازه قاعده دیگر d: اندازه ساق دیگر | |
| لوزی |
a: ضلع لوزی | |
| متوازیالاضلاع |
a: اندازه یکی از ضلعها b: اندازه ضلع مجاور a | |
|
a: یکی از ضلعها x: قطر اول y: قطر دوم | ||
|
a: یکی از ضلعها h: ارتفاع نظیر a θ: یکی از زایههای داخلی | ||
| بیضی (تقریب دایره) |
a: شعاع بزرگ بیضی b: شعاع کوچک بیضی | |
| چندضلعی منتظم |
n: تعداد ضلعها s: اندازه هر ضلع | |
| چندضلعی نامنتظم | - |
مجموع ضلعها |
| مکعب مربع |
a: اندازه یکی از لبهها | |
| مکعب مستطیل |
l: اندازه طول w: اندازه عرض h: اندازه ارتفاع | |
| منشور |
p: محیط قاعده منشور H: ارتفاع وجههای جانبی | |
| استوانه |
d: قطر h: ارتفاع | |
|
r: شعاع قاعده | ||
| کره |
r: شعاع کره | |
| هرم |
p: محیط قاعده s: مجموع ساقهای وجههای جانبی | |
|
p: محیط قاعده | ||
| مخروط |
r: شعاع قاعده |
محیط شکل های هندسی دوبعدی چیست ؟
محیط، طول خط یا منحنی تشکیلدهنده شکلهای بسته دوبعدی بسته است. در این بخش، قصد داریم به معرفی فرمولهای محاسبه محیط شکلهای دوبعدی شناختهشده نظیر مثلث، مربع، مستطیل، دایره و غیره بپردازیم.
محیط مثلث چیست ؟
مثلث، شکلی است که از سه ضلع تشکیل میشود. بر اساس تعریف، محیط مثلث از مجموع اندازه سه ضلع آن به دست میآید. فرمول محیط مثلث به صورت زیر نوشته میشود:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
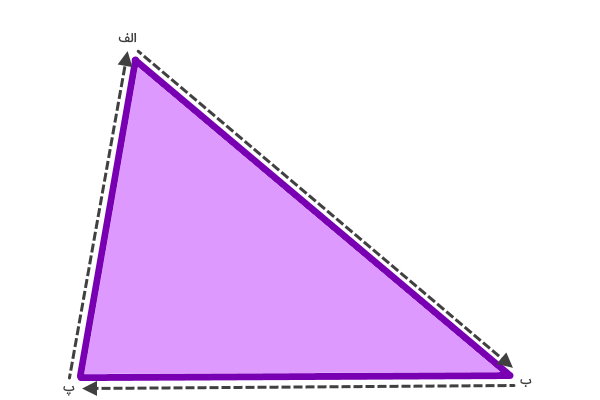
در تصویر بالا، مسیر دور یک مثلث مختلفالاضلاع (مثلث الف ب پ) نمایش داده شده است. با توجه به فرمول محیط مثلث داریم:
(پ الف) + (ب پ) + (الف ب) = محیط مثلث (الف ب پ)
عبارت جبری محیط مثلث برابر است با:
- P: محیط مثلث
- a: اندازه ضلع اول
- b: اندازه ضلع دوم
- c: اندازه ضلع سوم
مثلثها، انواع مختلفی دارند که از مهمترین آنها میتوان به مثلث متساویالساقین، مثلث متساویالاضلاع و مثلث قائمالزاویه اشاره کرد. در حالت کلی، محاسبه محیط این مثلثها با فرمول محیط مثلث مختلفالاضلاع (رابطه بالا) انجام میگیرد. با این وجود، روشهای دیگری نیز برای حالتهای خاص مثلث وجود دارد.
محیط مثلث متساوی الاضلاع چیست ؟
مثلث متساویالاضلاع، مثلثی با ضلعهای هماندازه است. بنابراین، فرمول محیط متساویالاضلاع به صورت زیر نوشته میشود:
ضلع + ضلع + ضلع = محیط مثلث متساویالاضلاع
ضلع × ۳ = محیط مثلث متساویالاضلاع
- P: محیط مثلث متساویالاضلاع
- a: اندازه یک ضلع
محیط مثلث متساوی الساقین چیست ؟
مثلث متساویالساقین، مثلثی است که دو ضلع هماندازه دارد. به این ضلعها، ساق و به ضلع سوم، قاعده میگویند. محیط مثلث متساوی الساقین از فرمول زیر به دست میآید:
قاعده + ساق + ساق = محیط مثلث متساویالساقین
قاعده + (ساق × ۲) = محیط مثلث متساویالساقین
- P: محیط مثلث متساویالساقین
- l: اندازه ساق
- b: اندازه قاعده
محیط مثلث قائم الزاویه چیست ؟
مثلث قائمالزاویه، مثلثی با یک زاویه ۹۰ درجه است. در این مثلث، با دانستن اندازه دو ضلع، امکان تعیین ضلع سوم و در نتیجه محاسبه محیط فراهم میشود. به ضلعهای زاویه ۹۰ درجه، ساق و به ضلع مقابل به این زاویه، وتر میگویند. بر این اساس، فرمول محیط مثلث قائمالزاویه به صورت زیر نوشته میشود:
یا
- P: محیط مثلث قائمالزاویه
- a: اندازه یکی از ساقها
- b: اندازه ساق دیگر
- c: اندازه وتر
اگر مثلث قائمالزاویه دارای دو ساق هماندازه باشد، فرمول محاسبه محیط آن به شکل زیر در میآید:
- P: محیط مثلث قائمالزاویه
- a: اندازه یکی از ساقها
مثلث، یکی از مهمترین شکلهای هندسی به شمار میرود. تمام چندضلعیها را میتوان به صورت مجموعهای از چند مثلث بهمچسبیده نمایش داد. از اینرو، بهترین شکل برای یادگیری مبحث محیط، مثلث خواهد بود.
مجموعه مقالات مرتبط با این بخش:
مثال ۲: محاسبه محیط مثلث
محیط مثلث زیر را تعیین کنید. (واحدها بر حسب سانتیمتر هستند.)
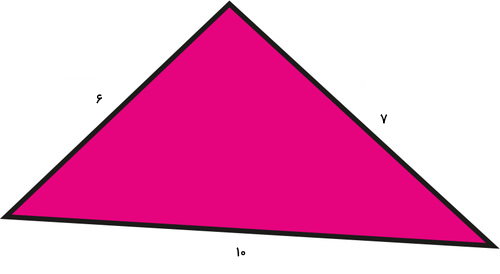
محیط مثلث، از مجموع طول سه ضلع آن به دست میآید. فرمول محیط این شکل به صورت زیر نوشته میشود:
ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث
۶ + ۱۰ + ۷ = محیط مثلث
۲۳ = محیط مثلث
در نتیجه، محیط مثلث برابر با ۲۳ سانتیمتر است.
محیط مربع چیست ؟
مربع، یکی از انواع چندضلعیهای منتظم است که از چهار ضلع با اندازههای برابر تشکیل میشود. به دلیل برابر بودن ضلعهای این شکل، فقط با داشتن اندازه یکی از ضلعها میتوان محیط آن را به دست آورد. فرمول محیط مربع به صورت زیر نوشته میشود:
ضلع + ضلع + ضلع + ضلع = محیط مربع
ضلع × ۴ = محیط مربع

در تصویر بالا، خط سیاه بر روی محیط مربع حرکت میکند. اگر اندازه هر ضلع این مربع را برابر با a در نظر بگیریم، عبارت جبری محیط مربع به صورت زیر خواهد بود:
- P: محیط مربع
- a: ضلع مربع
اندازه ضلعهای مربع با اندازه قطرهای آن رابطه دارد. بر اساس قضیه فیثاغورس، قطر مربع برابر با برابر ضلع آن است. به این ترتیب، فرمول محیط مربع را میتوان بر حسب قطر نیز نوشت:
- P: محیط مربع
- d: قطر مربع
مجموعه مقالات مرتبط با این بخش:
مثال ۳: محاسبه محیط مربع
محیط مربعی به ضلع ۱۲/۵ میلیمتر را محاسبه کنید.
در مربع، اندازه تمام ضلعها با یکدیگر برابر هستند. بنابراین، محیط این شکل از ضرب تعداد ضلعهای آن در اندازه یکی از ضلعها به دست میآید:
اندازه یک ضلع × ۴ = محیط مربع
۱۲/۵ × ۴ =
۵۰ =
در نتیجه، محیط مربع برابر با ۵۰ میلیمتر است.
محیط مستطیل چیست ؟
مستطیل، یک چهارضلعی غیر منتظم است که چهار زاویه ۹۰ درجه دارد. ضلعهای روبهرویی این شکل، با یکدیگر موازی و مساوی هستند. به ضلعهای مستطیل، طول و عرض میگویند. با توجه به این موضوع، فرمول محیط مستطیل به صورت زیر نوشته میشود:
عرض + طول + عرض + طول = محیط مستطیل
(عرض × ۲) + (طول × ۲) = محیط مستطیل
(عرض + طول) × ۲ = محیط مستطیل

در ریاضیات، معمولا طول اشکال هندسی را با حرف انگلیسی l و عرض آنها را با حرف انگلیسی w نمایش میدهند. بر این اساس، عبارت جبری محیط مستطیل برابر خواهد بود با:
- P: محیط مستطیل
- l: طول مستطیل
- w: عرض مستطیل
استفاده از اندازه قطر برای محاسبه محیط مستطیل مرسوم نیست. با این حال، در صورت دانستن این اندازه و یکی از اندازههای طول یا عرض، امکان تعیین محیط با استفاده از فرمول زیر فراهم میشود:
- P: محیط مستطیل
- l: طول مستطیل (یا عرض مستطیل)
- d: قطر مستطیل
مجموعه مقالات مرتبط با این بخش:
مثال ۴: محاسبه محیط مستطیل
شخصی قصد دارد دور یک زمین ورزشی مستطیلی، پیادهروی کند. طول این زمین برابر با ۴۳ متر و عرض آن برابر با ۲۷ متر است. این شخص پس از یک دور کامل، چه مسافتی را طی میکند؟
منظور از دور زمین ورزشی، محیط آن است. با پیادهروی به اندازه یک دور کامل، شخص مسافتی معادل با محیط زمین ورزشی را طی میکند. این زمین به شکل مستطیل است. بنابراین، محیط آن را با استفاده از فرمول محیط مستطیل به دست میآوریم:
(عرض + طول) × ۲ = محیط مستطیل
(عرض زمین + طول زمین) × ۲ = محیط زمین
(۲۷ + ۴۳) × ۲ =
(۷۰) × ۲ =
۱۴۰ =
در نتیجه، محیط زمین ورزشی برابر با ۱۴۰ متر است. به عبارت دیگر، شخص با زدن یک دور کامل، مسافتی معادل ۱۴۰ متر را طی میکند.
محیط دایره چیست ؟
دایره، یکی دیگر از شکلهای اصلی و پایه هندسی است. برخلاف دیگر شکلهای پایه، دایره از یک منحنی بسته تشکیل میشود. شعاع و قطر دایره، اهمیت بسیار بالایی در محاسبه محیط آن دارند. علاوه بر این اندازهها، عدد پی (۳/۱۴) نیز تقریبا در تمام محاسبات این شکل مورد استفاده قرار میگیرد.
فرمول محیط دایره به صورت زیر نوشته میشود:
قطر × ۳/۱۴ = محیط دایره
شعاع × ۳/۱۴ × ۲ = محیط دایره
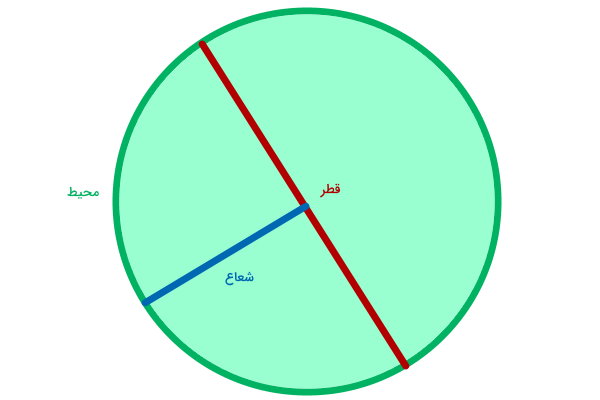
در تصویر بالا، مداد بر روی محیط دایره حرکت میکند. در ریاضیات، معمولا شعاع دایره را با حرف انگلیسی r، قطر آن را با حرف انگلیسی d و عدد پی را با حرف یونانی π نمایش میدهند. برخلاف چندضلعیها، نماد محیط در دایره، حرف انگلیسی C (ابتدای کلمه Circumference) است. به این ترتیب، عبارت جبری محیط دایره به صورت زیر نوشته میشود:
- C: محیط دایره
- π: عدد ثابت ۳/۱۴
- d: قطر دایره
- r: شعاع دایره
مجموعه مقالات مرتبط با این بخش:
مثال ۵: محاسبه قطر دایره از روی محیط
محیط دایره زیر برابر با ۹/۴۲ متر است. اندازه قطر آن را به دست بیاورید.
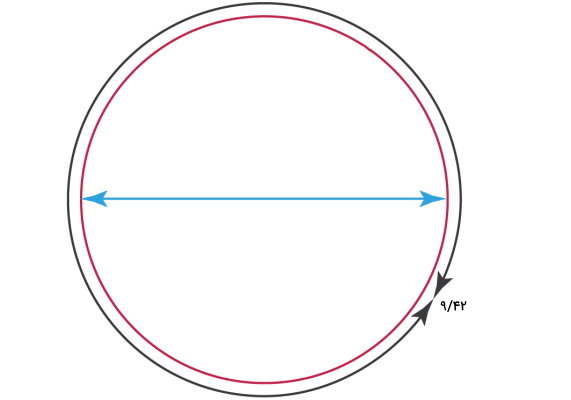
محیط دایره از فرمول زیر محاسبه میشود:
قطر × عدد پی = محیط دایره
قطر × ۳/۱۴ = ۹/۴۲
۳/۱۴ ÷ ۹/۴۲ = قطر
۳ = قطر
در نتیجه، قطر دایره برابر با ۳ متر است.
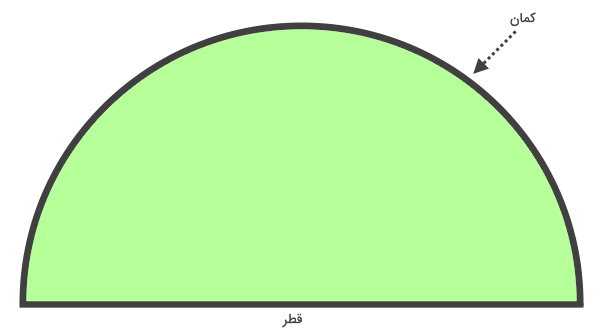
محیط نیم دایره چیست ؟
قطر دایره، این شکل را به دو قسمت مساوی تقسیم میکند. به هر یک از این قسمتها، نیمدایره میگویند. این شکل، از یک کمان و یک قطر تشکیل میشود. اندازه کمان نیمدایره برابر با نصف محیط دایره است. به این ترتیب، محیط نیمدایره از فرمول زیر به دست میآید:
قطر + نصف محیط دایره کامل = محیط نیمدایره
عبارت جبری محیط نیمدایره به صورت زیر نوشته میشود:
یا
- CS: محیط نیمدایره
- π: عدد ثابت ۳/۱۴
- r: شعاع دایره
- d: قطر دایره
- π: عدد ثابت ۳/۱۴
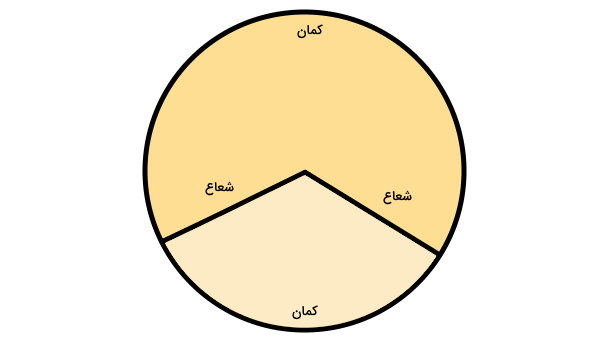
محیط قطاع دایره چیست ؟
قطاع، بخشی از یک دایره کامل است که از یک کمان و دو شعاع تشکیل میشود. نیمدایره (یکدوم دایره) و ربعدایره (یکچهارم دایره)، از قطاعهای شناختهشده هستند. محیط این شکل هندسی از جمع طول کمان و دو شعاع دایره به دست میآید:
(شعاع × ۲) + کمان = محیط قطاع
عبارت جبری محیط قطاع دایره به صورت زیر نوشته میشود:
- CSe: محیط قطاع دایره
- l: طول کمان
رابطه طول کمان دایره نیز عبارت است از:
- l: طول کمان
- r: شعاع دایره
- θ: زاویه کمان بر حسب رادیان
تبدیل واحد درجه به رادیان با استفاده از فرمول زیر انجام میشود:
۱۸۰ ÷ (π × درجه) = رادیان
محیط ذوزنقه چیست ؟
ذوزنقه، چهارضلعی است که فقط دو ضلع آن با هم موازی باشند. به ضلعهای موازی این شکل، قاعده و به ضلعهای غیر موازی آن، ساق میگویند. محیط ذوزنقه از فرمول زیر به دست میآید:
ساق دوم + قاعده دوم + ساق اول + قاعده اول = محیط ذوزنقه
(مجموع قاعدهها) + (مجموع ساقها) = محیط ذوزنقه
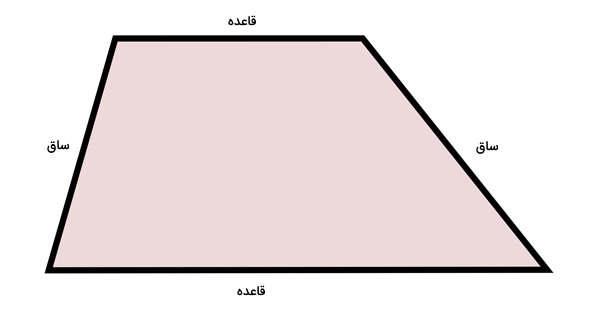
عبارت جبری محیط ذوزنقه به صورت زیر نوشته میشود:
- P: محیط ذوزنقه
- a: اندازه یکی از قاعدهها
- b: اندازه یکی از ساقها
- c: اندازه قاعده دیگر
- d: اندازه ساق دیگر
ذوزنقه، انواع مختلفی دارند. در تصویر بالا، نوع مختلفالاضلاع این شکل را مشاهده کردید. محیط ذوزنقه مختلفالاضلاع برای تمام ذوزنقهها قابل استفاده است.
محیط ذوزنقه متساوی الساقین چیست ؟
اگر ساقهای یک ذوزنقه با یکدیگر برابر باشند، به آن ذوزنقه متساویالساقین میگویند. محیط این ذوزنقه از فرمول زیر به دست میآید:
(مجموع قاعدهها) + (ساق × ۲) = محیط ذوزنقه متساوی الساقین
محیط ذوزنقه قائم الزاویه چیست ؟
ذوزنقه قائمالزاویه، یک زاویه راست دارد. در صورت دانستن اندازه سه ضلع این شکل، امکان محاسبه اندازه ضلع چهارم و محیط آن فراهم میشود. فرمول محیط ذوزنقه قائمالزاویه، عبارت است از:
- P: محیط ذوزنقه
- a: اندازه یکی از قاعدهها
- b: اندازه یکی از ساقها
- c: اندازه قاعده دیگر
- h: ساق قائمه
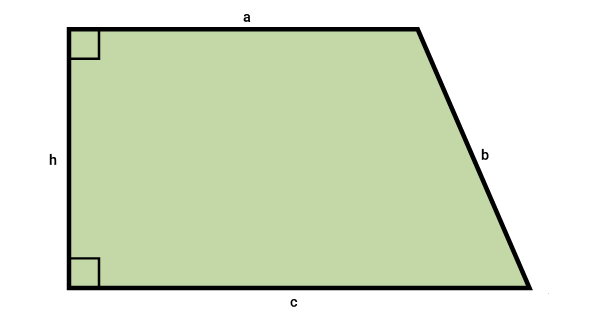
اندازه ساق قائمه به کمک قضیه فیثاغورس نوشته میشود:
- h: ساق قائمه
- a: قاعده کوچک
- b: قاعده بزرگ
- c: ساق دیگر
مثال ۶: محاسبه محیط ذوزنقه
یک ذوزنقه متساویالساقین به ساق ۷ سانتیمتر، قاعده بزرگ ۱۵ سانتیمتر و قاعده کوچک ۱۲ سانتیمتر را در نظر بگیرید. محیط این ذوزنقه چقدر است؟
ذوزنقه، چهار ضلع دارد. در ذوزنقه متساویالساقین، اندازه ساقها با یکدیگر برابرند. محیط این نوع ذوزنقه با استفاده از فرمول محاسبه میشود:
(مجموع قاعدهها) + (ساق × ۲) = محیط ذوزنقه
(۱۲ + ۱۵) + (۷ × ۲) =
(۲۷) + (۱۴) =
۴۱ =
در نتیجه، محیط ذوزنقه متساویالساقین برابر با ۴۱ سانتیمتر است.
محیط لوزی چیست ؟
لوزی، نوعی چهارضلعی با ضلعهای برابر است که دو زاویه منفرجه و دو زاویه حاده دارد.
محیط این شکل نیز مانند محیط مربع، از ضرب اندازه یک ضلع در عدد ۴ به دست میآید:
ضلع × ۴ = محیط لوزی
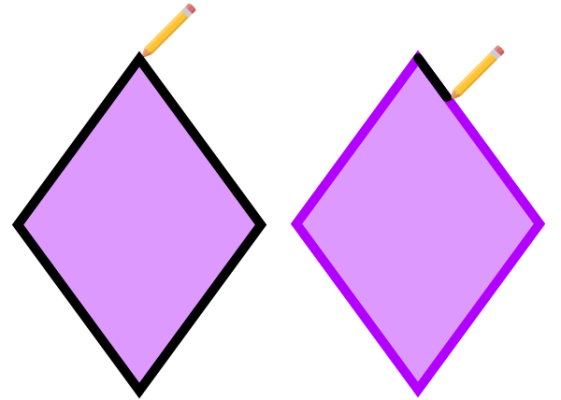
عبارت جبری محیط لوزی به صورت زیر نوشته میشود:
- P: محیط لوزی
- a: ضلع لوزی
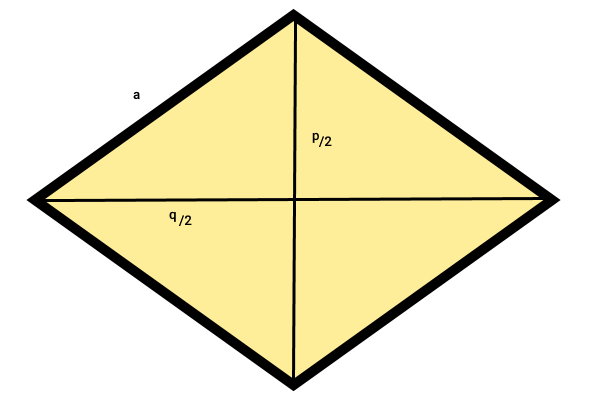
فرمول محیط لوزی با قطر، عبارت است از:
- P: محیط لوزی
- p: اندازه یکی از قطرها
- q: اندازه قطر دیگر
مجموعه مقالات مرتبط با این بخش:
مثال ۷: محاسبه محیط لوزی
اندازه ضلع یک لوزی با محیط ۳۹/۴۴ واحد طول را تعیین کنید.
محیط لوزی از رابطه زیر به دست میآید:
ضلع × ۴ = محیط لوزی
اندازههای معلوم را درون رابطه بالا قرار میدهیم:
ضلع × ۴ = ۳۹/۴۴
۴ ÷ ۳۹/۴۴ = ضلع
۹/۸۶ = ضلع
در نتیجه، اندازه هر ضلع لوزی برابر با ۹/۸۶ واحد طول است.
محیط متوازی الاضلاع چیست ؟
متوازیالاضلاع، یک نوع چهارضلعی است که ضلعهای آن دو به دو با هم موازی و مساوی هستند. فرمولهای محیط متوازیالاضلاع، به فرمولهای محیط مستطیل شباهت دارند:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط متوازیالاضلاع
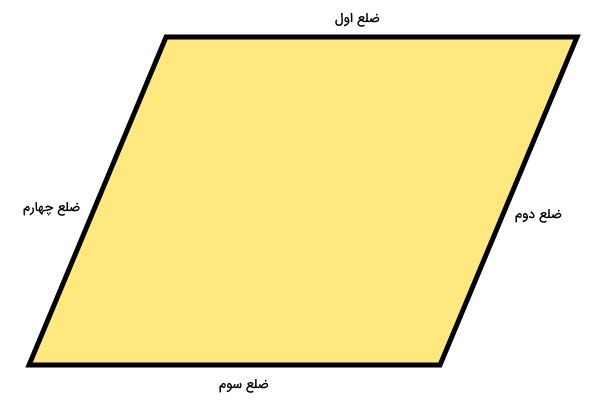
(ضلع دوم × ۲) + (ضلع اول × ۲) = محیط متوازیالاضلاع
(ضلع دوم + ضلع اول) × ۲ = محیط متوازیالاضلاع
(مجموع دو ضلع مجاور) × ۲ = محیط متوازیالاضلاع
عبارت جبری محیط متوازیالاضلاع عبارت است از:
- P: محیط
- a: اندازه یکی از ضلعها
- b: اندازه ضلع مجاور a
مجموعه مقالات مرتبط با این بخش:
مثال ۸: محاسبه محیط متوازیالاضلاع
تصویر زیر، اندازه دو ضلع مجاور یک متوازیالاضلاع را نمایش میدهد. محیط این متوازیالاضلاع را به دست بیاورید.
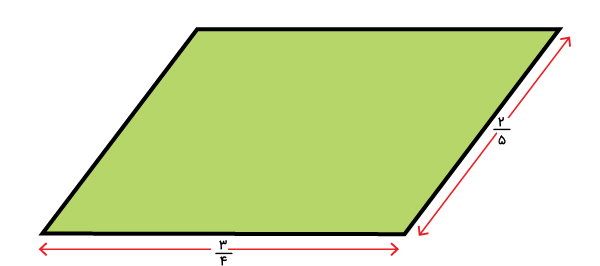
فرمول محیط متوازیالاضلاع عبارت است از:
- P: محیط
- a: اندازه یکی از ضلعها
- b: اندازه ضلع مجاور a
به جای a و b، مقادیر نمایش داده شده در تصویر را درون فرمول قرار میدهیم:
برای عبارتهای کسری، از آنها مخرج مشترک میگیریم:
در نتیجه، محیط متوازیالاضلاع برابر با ۲/۳ است.
محیط بیضی چیست ؟
بیضی، منحنی بستهای است که به یک دایره کشیده یا فشرده شده شباهت دارد. البته برخلاف دایره، بیضی دارای دو نقطه کانونی است. مجموع تمام نقاط روی محیط بیضی از این دو کانون، یک عدد ثابت میشود. محیط بیضی از روشهای تقریبی به دست میآید.
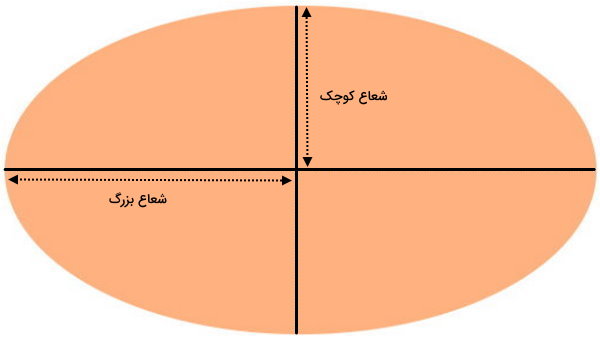
سادهترین تقریب محیط بیضی عبارت است از:
- P: محیط بیضی
- a: شعاع بزرگ بیضی
- b: شعاع کوچک بیضی
این فرمول، برای محاسبه محیط بیضیهای شبیه به دایره کاربرد دارد. انتگرال زیر، بهترین فرمول محیط بیضی است:
البته برای رسیدن به یک جواب مشخص، باید فرم پارامتری انتگرال بالا را بنویسیم:
تا کنون، چندین تقریب برای محاسبه محیط بیضی ارائه شدهاند. دقت هر یک از این تقریبها در شرایط مختلف با یکدیگر تفاوت دارد. به علاوه، برخی از آنها به قدری پیچیده هستند که برای حلشان فقط از کامپیوتر استفاده کرد.
مجموعه مقالات مرتبط با این بخش:
محیط چندضلعی منتظم چیست ؟
به چندضلعیهایی که اندازه تمام ضلعها و زاویههای آنها با یکدیگر برابر است، چندضلعی منتظم میگویند. در بخشهای قبلی، دو مورد از شناختهشدهترین چندضلعیهای منتظم، یعنی مثلث متساویالاضلاع و مربع را معرفی کردیم.
محیط این شکلها از ضرب اندازه ضلعها در تعداد ضلعها به دست میآمد. محیط دیگر چندضلعیهای منتظم نیز به همین شکل محاسبه میشود:
اندازه ضلع × تعداد ضلع = محیط چندضلعی منتظم
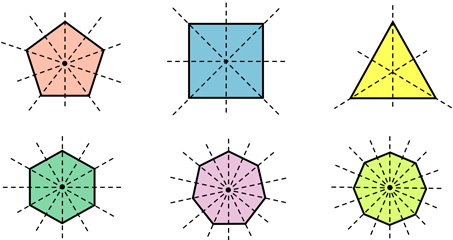
عبارت جبری محیط چندضلعی منتظم برابر است با:
- P: محیط چندضلعی منتظم
- n: تعداد ضلعهای چندضلعی منتظم
- s: اندازه هر ضلع
مجموعه مقالات مرتبط با این بخش:
مثال ۹: محاسبه محیط چندضلعی منتظم
محیط یک هشتضلعی منتظم به طول ضلع ۸ سانتیمتر را حساب کنید.
محیط چندضلعیهای منتظم از ضرب تعداد ضلعها در اندازه یک ضلع به دست میآید. به زبان ریاضی داریم:
- P: محیط هشتضلعی منتظم
- n: تعداد ضلعها برابر با ۸
- s: اندازه هر ضلع برابر با ۸ سانتیمتر
در نتیجه، محیط یک هشتضلعی منتظم به ضلع ۸ سانتیمتر برابر با ۶۴ سانتیمتر است.
محیط چندضلعی نامنظم چیست ؟
شکلهای نامنظم یا غیر منتظم، شکلهایی هستند که تمام ضلعهای آنها با یکدیگر برابر نیستند. در بخشهای قبلی، نحوه محاسبه محیط برخی از شکلهای نامنظم نظیر مثلث، مستطیل، ذوزنقه و متوازیالاضلاع را توضیح دادیم. این شکلها، با وجود نامنظم بودن، ویژگیهایی داشتند که امکان تعریف فرمول مخصوص برای تعیین محیط آنها را فراهم میکرد. با این حال، تمام شکلهای نامنظم به این صورت نیستند. به عنوان مثال، شکلهای زیر را در نظر بگیرید.
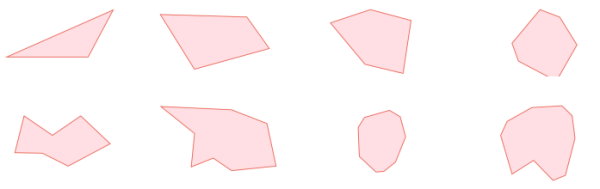
تعریف کلی محیط برای شکلهای بالا، هیچ تفاوتی با تعریف محیط با شکلهای منظم ندارد. محیط شکلهای نامنظم، اندازه یا مسافت دور آنها است. در نتیجه، برای محاسبه محیط این شکلها باید اندازه تمام ضلعها را با هم جمع کرد.
مثال ۱۰: محاسبه محیط چندضلعی نامنظم
محیط شکل نامنظم زیر را پیدا کنید. (قسمت منحنی شکل، یک نیمدایره است.)
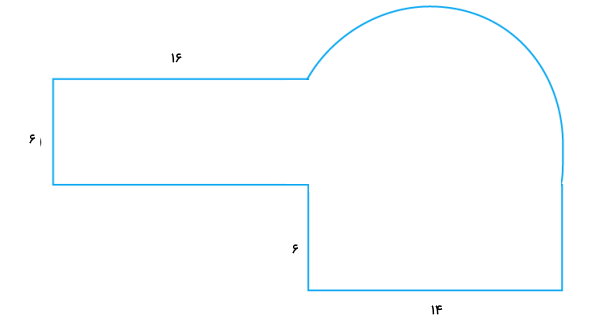
محیط شکلهای نامنظم، از جمع اندازه ضلعها و یا منحنیها تشکیلدهنده آنها به دست میآید. به منظور تعیین محیط شکل بالا، ابتدا آن را به چندین شکل شناختهشده تقسیم میکنیم و سپس اندازههای معلوم را بر روی بخشهای مختلف مینویسیم.
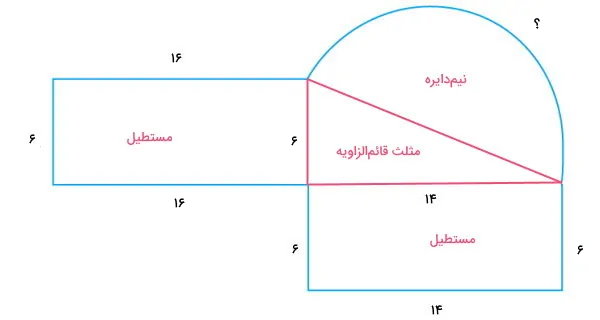
مجموع طول خطوط آبی، اندازه محیط شکل است. از بین اندازههای مورد نیاز، طول کمان نیمدایره را نداریم. برای محاسبه این اندازه، باید شعاع یا قطر آن را به دست بیاوریم. بر اساس شکل بالا، وتر مثلث قائمالزاویه، همان قطر نیمدایره است. با استفاده از اندازه ساقها و قضیه فیثاغورس میتوان اندازه این وتر (قطر نیمدایره) را محاسبه کنیم:
- c: وتر مثلث قائمالزاویه
- a: اندازه یکی از ساقها برابر با ۶
- b: اندازه ساق دیگر برابر با ۱۴
طول کمان نیمدایره، برابر با نصف محیط دایره کامل است. محیط دایره کامل به صورت زیر محاسبه میشود:
قطر × ۳/۱۴ = محیط دایره کامل
۱۵/۲۳ × ۳/۱۴ =
۴۷/۸۲ =
بنابراین:
۲ ÷ ۴۷/۸۲ = محیط نیمدایره
۲۳/۹۱ =
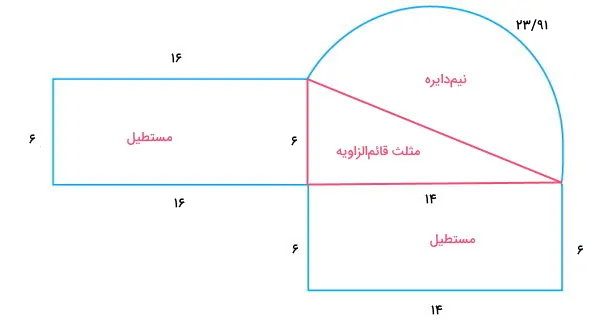
اکنون، تمام اندازههای مورد نیاز برای محیط شکل را داریم. از اینرو، طول تمام خطوط آبی را با هم جمع میکنیم:
۲۳/۹۱ + ۶ + ۱۴ + ۶ + ۱۶ + ۶ + ۱۶ = محیط شکل
۸۷/۹۱ =
در نتیجه، محیط شکل نامنظم برابر با ۸۷/۹۱ واحد طول است.
محیط شکل های هندسی سه بعدی چیست ؟
محیط، به عنوان اندازه دور شکلهای دوبعدی در نظر گرفته میشود. از اینرو، تعریف محیط در شکلهای سهبعدی، تفاوت دارد. در چندوجهیها، به مجموع طول لبههای شکل، محیط میگویند. در برخی از موارد نیز، اندازه دور تصویر شکل سهبعدی بر روی صفحه را به عنوان محیط در نظر میگیرند. در ادامه، به معرفی نحوه محاسبه محیط برخی از شکلهای سهبعدی میپردازیم.
محیط مکعب مربع چیست ؟
مکعب مربع، یک شکل سهبعدی است که از شش وجه مربعی شکل و برابر تشکیل میشود. این شکل، ۱۲ لبه هماندازه دارد. محیط مکعب مربع، از جمع طول این ۱۲ لبه به دست میآید. فرمول محیط مکعب مربع عبارت است از:
اندازه یک لبه × ۱۲ = محیط مکعب
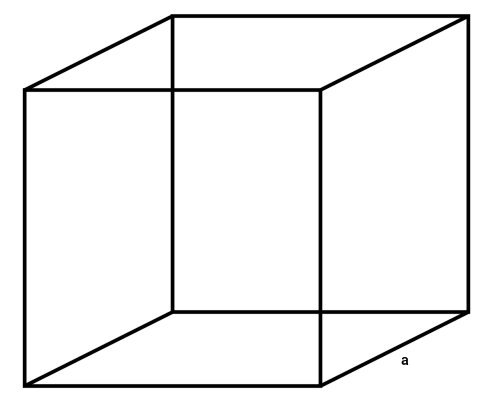
عبارت جبری محیط مکعب مربع به صورت زیر نوشته میشود:
- P: محیط مکعب مربع
- a: اندازه یکی از لبهها
توجه داشته باشید که برای تعیین محیط چندوجهیها، جمع کردن ضلعهای وجهها اشتباه است؛ چراکه وجهها دارای ضلعهای مشترک هستند. بنابراین، در محاسبه محیط باید طول لبهها (فاصله بین گوشهها) را در نظر گرفت.
محیط مکعب مستطیل چیست ؟
مکعب مستطیل، یک شش وجهی مستطیلی شکل است. محاسبه محیط این شکل سهبعدی نیز مانند محاسبه محیط مکعب مربع، با جمع طول لبهها انجام میگیرد. مکعب مستطیل دارای سه اندازه اصلی طول، عرض و ارتفاع است. با توجه به این موضوع، محیط این شکل از رابطه زیر به دست میآید:
(ارتفاع + عرض + طول) × ۴ = محیط مکعب مستطیل
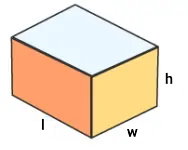
عبارت جبری محیط مکعب مستطیل به صورت زیر نوشته میشود:
- P: محیط مکعب مستطیل
- l: اندازه طول
- w: اندازه عرض
- h: اندازه ارتفاع
محیط منشور چیست ؟
منشور، شکلی است که از دو قاعده n ضلعی مشابه و n وجه کناری به شکل متوازیالاضلاع/مستطیل تشکیل میشود. تعداد لبههای هر منشور، برابر با ۳n است. محیط این شکل، از جمع طول این لبهها به دست میآید. البته در برخی از موارد، محیط قاعده، به عنوان محیط منشور در نظر گرفته میشود. فرمول محیط منشور عبارت است از:
(ارتفاع منشور × تعداد ضلعهای قاعده) + (محیط قاعده × ۲) = محیط منشور
تصویر زیر، نمونهای از یک منشور مثلثی را نمایش میدهد.
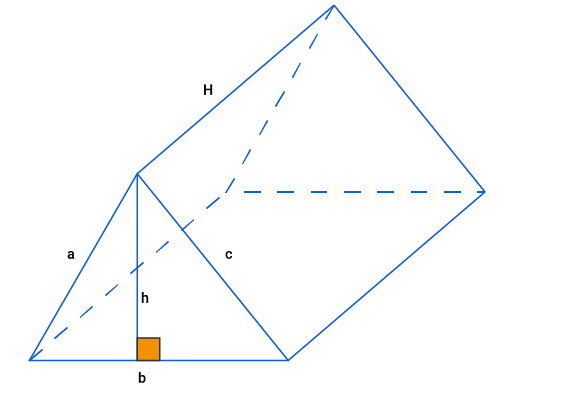
بر اساس اندازههای نمایش داد شده، محیط شکل بالا به صورت زیر محاسبه میشود:
عبارت جبری محیط منشور را میتوانیم به صورت زیر بنویسیم:
- P: محیط منشور
- p: محیط قاعده منشور
- H: ارتفاع وجههای جانبی منشور
محیط استوانه چیست ؟
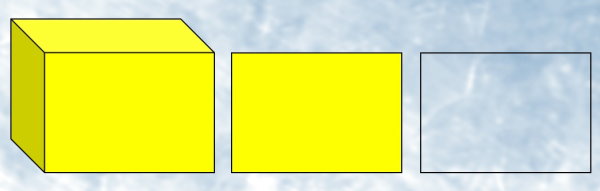
استوانه، شکلی است که از گسترش یک دایره در بعد سوم به وجود میآید. برخلاف چندوجهیها، امکان جمع کردن لبههای این شکل برای به دست آوردن محیط آن وجود ندارد؛ چراکه استوانه هیچ لبهای ندارد. با این حال، اگر استوانه را به بر روی یک صفحه تصویر کنیم، امکان محاسبه محیط فراهم میشود.

شکل بالا، تصویر استوانه بر روی صفحه افقی و عمودی را نمایش میدهد. در شکل سمت راست، مستطیلی به طول برابر با ارتفاع استوانه و عرض برابر با قطر قاعده به وجود آمده است. محیط استوانه در این حالت از رابطه زیر به دست میآید:
(ارتفاع × ۲) + (قطر قاعده × ۲) = محیط استوانه
در شکل سمت چپ، تصویر استوانه یه شکل یک دایره درآمده است. محیط استوانه در این حالت به صورت زیر محاسبه میشود:
شعاع قاعده × عدد پی × ۲ = محیط استوانه
در مجموع، به خاطر داشته باشید که شکلهای سهبعدی، مخصوصا سطوح منحنی نظیر استوانه و کره، محیط ندارند. بنابراین در اغلب موارد، منظور از محیط این شکلها، محیط تصویر یا قاعده آنها است.
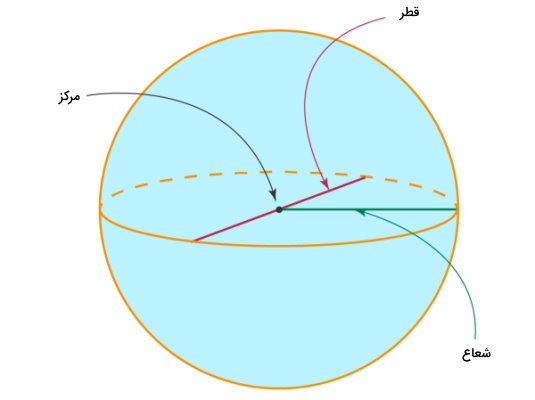
محیط کره چیست ؟
کره، مجموعه نقاطی در فضای سهبعدی است که از یک نقطه ثابت، به اندازه برابر فاصله دارند. منظور از محیط کره، معمولا محیط بزرگترین دایرهای است که میتوان در اطراف آن کشید. این دایره، همان تصویر دوبعدی کره بر روی یک صفحه سهبعدی است. بنابراین، فرمول محیط کره به صورت زیر نوشته میشود:
شعاع کره × عدد پی × ۲ = محیط کره
محیط هرم چیست ؟
هرم، شکلی است که از اتصال یک قاعده چندضلعی به نقطهای در خارج از آن (راس) تشکیل میشود. بر اساس تعریف محیط در چندوجهیها، محیط هرم برابر با مجموع طول لبههای آن است. به این ترتیب، فرمول محیط هرم به صورت زیر نوشته میشود:
مجموع ساقهای وجههای کناری + محیط قاعده = محیط هرم
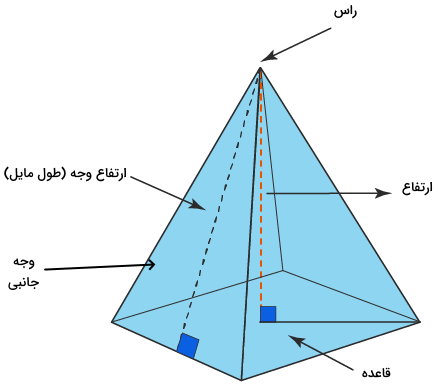
در برخی از مواقع، منظور از محیط هرم، محیط قاعده آن است. قاعده هرم میتواند مثلث، مربع، مستطیل، ذوزنقه و هر چندضلعی منتظم یا غیر منتظمی باشد.
محیط مخروط چیست ؟
مخروط، شکلی مشابه هرم و با قاعده دایره است. این شکل، وجه کناری ندارد و نمیتوان محیط آن را با جمع اندازه لبهها به دست آورد. به همین دلیل، در اغلب موارد، منظور از محیط مخروط، محیط قاعده آن است. این محیط توسط فرمول محیط دایره محاسبه میشود:
شعاع × عدد پی × ۲ = محیط مخروط
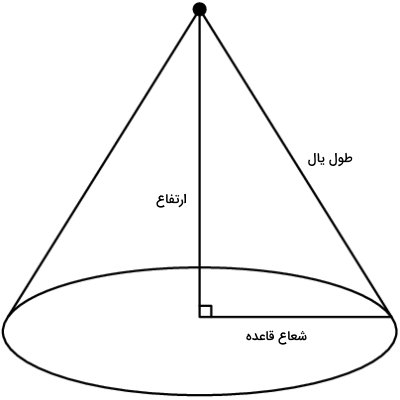
در برخی از موارد، اندازه دور مقطع طولی (برش عمودی) مخروط را به عنوان محیط آن در نظر میگیرند. در این حالت، محیط مخروط برابر است با:
(شعاع قاعده + یال) × ۲ = محیط مخروط
تفاوت محیط با مساحت و حجم چیست ؟
محیط، مساحت و حجم، از مفاهیم پرکاربرد در هندسه هستند. تفاوتهای واضحی بین این مفاهیم وجود دارد که در جدول زیر به معرفی برخی از آنها پرداختهایم.
| محیط | مساحت | حجم |
| کمیت یکبعدی | کمیت دوبعدی | کمیت سهبعدی |
| مرز یا مسافت دور اطراف اشکال بسته دوبعدی | سطح یا محدوده درون اشکال بسته دوبعدی | ظرفیت یا فضای اشغال شده توسط اشکال سهبعدی |
| واحد طول (m) | مربع واحد طول (m۲) | مکعب واحد طول (m۳) |
عملیاتهای ریاضی و تعداد متغیرهای مورد استفاده برای محاسبه محیط، مساحت و حجم، مطابق با بُعد آنها است. به عنوان مثال، محیط یک شکل هندسی، معمولا با جمع چندین متغیر دارای واحد طول یا ضرب یک متغیر دارای واحد طول انجام میگیرد.
جدول زیر، برخی از فرمولهای محیط، مساحت و حجم را با هم مقایسه میکند.
| شکل | محیط | مساحت | حجم |
| مربع | - | ||
| مکعب مربع | - | - | |
| مستطیل | - | ||
| مکعب مستطیل | - | - | |
| دایره | - | ||
| استوانه | - | - |
محاسبه آنلاین محیط شکل های هندسی
استفاده از محاسبهگرهای آنلاین، یکی از روشهای مناسب برای تعیین محیط شکلهای مختلف و یادگیری نحوه انجام محاسبات مربوط به آن است. سایتهای متعددی، امکان تعیین محیط را برای کاربران فراهم میکنند. از بهترین ماشینحسابهای محاسبه محیط آنلاین، میتوان به موتور جستجوی گوگل (+) و سایت Omni Calculator (+) اشاره کرد.
ماشین حساب محیط گوگل چیست ؟
کار کردن با محاسبهگر محیط گوگل، بسیار ساده است. در حال حاضر، برای استفاده از این ابزار باید عبارت انگلیسی شکلها را بلد باشید. به عنوان مثال، با جستجوی عبارت «Circumference» در موتور جستجوی گوگل، کادری مشابه تصویر زیر در ابتدای صفحه نتایج به نمایش درمیآید.
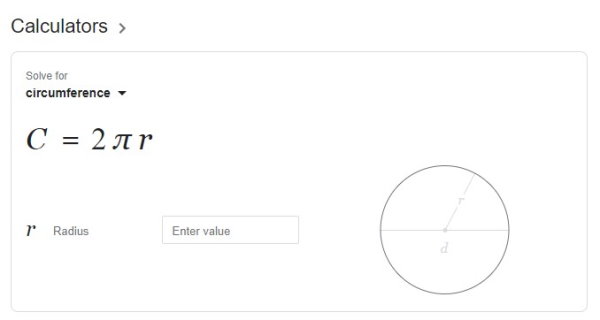
محاسبهگر محیط دایره در گوگل، با وارد کردن اندازه شعاع کار میکند. به این ترتیب، در صورت تایپ عدد شعاع، محیط دایره محاسبه شده و روند حل آن نشان داده میشود.
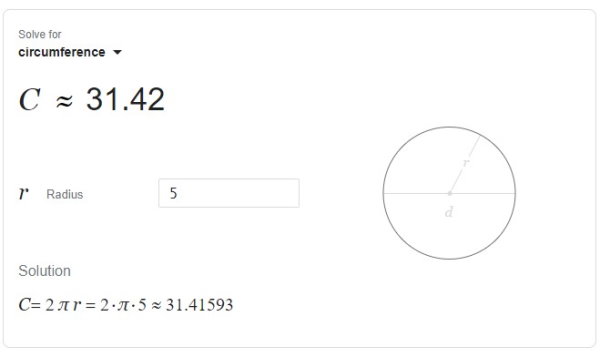
برای دسترسی به ماشینحساب محیط دیگر شکلها، در کنار عبارت مربوط به آنها (مثلا square برای مربع یا rectangle برای مستطیل)، از عبارت «perimeter» استفاده کنید.
ماشین حساب محیط Omni Calculator چیست ؟
سایت Omni Calculator، یک سایت تخصصی در زمینه ارائه ماشینحسابهای آنلاین است. ماشینحساب محیط Omni Calculator (+)، امکان انتخاب شکل مورد نظر و محاسبه محیط آن را فراهم میکند. با ورود به صفحه این ماشینحساب آنلاین، کادری مشابه تصویر زیر به نمایش در میآید.
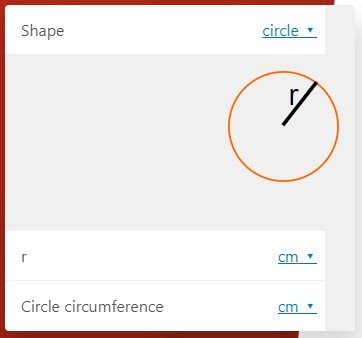
با کلیک بر روی منوی بازشونده مقابل عنوان «Shape»، فهرستی از شکلهای شناختهشده هندسی نشان داده میشود. به عنوان مثال، در اینجا برای محاسبه محیط مثلث، گزینه «triangle» را انتخاب میکنیم.
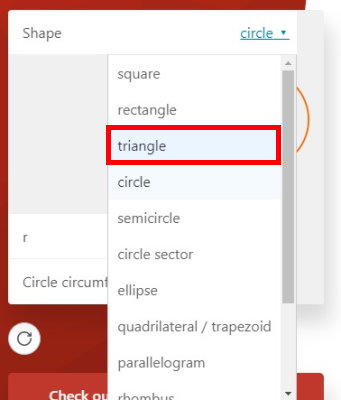
ماشینحساب محیط مثلث در Omni Calculator، گزینههای متعددی را در اختیار کاربران قرار میدهد. در تصویر زیر، محیط یک مثلث با استفاده از اندازه سه ضلع محاسبه شده است.
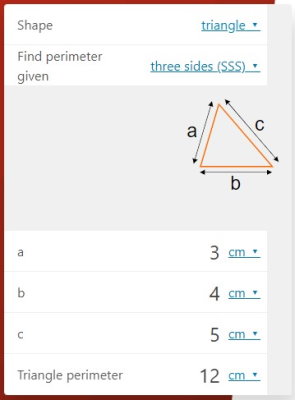
با تغییر گزینه مقابل عنوان «Find perimeter given»، امکان محاسبه محیط مثلث بل دو ضلع و زاویه بین و دو زاویه و ضلع بین نیز فراهم میشود.
اندازه گیری محیط با ابزارهای تخصصی
محیط، از مفاهیم کاربردی و محیط در حوزههای مهندسی و جغرافیایی است. در این بخش، نحوه محاسبه محیط توسط ابزارهای تخصصی این حوزهها را آموزش میدهیم.
اندازه گیری محیط در اتوکد
اتوکد، محبوبترین نرمافزار طراحی به کمک کامپیوتر است. این نرمافزار به منظور ترسیم المانهای دوبعدی و سهبعدی مورد استفاده قرار میگیرد. چندین روش برای اندازهگیری محیط شکلهای دوبعدی در اتوکد وجود دارد. سادهترین روش برای انجام این کار، اجرای دستور «MEASUREGEOM» یا همان ابزار «Area» در زبانه «Home»، بخش «Utilities» است. پس از اجرای این دستور و تعیین محدوده مورد نظر، اطلاعات مربوط به مساحت و محیط محدوده در بالای نوار خط فرمان به نمایش درمیآید.
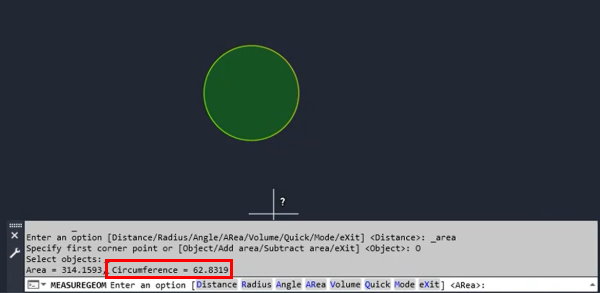
در تصویر بالا، محیط یک شی دایرهای محاسبه شده است. عدد مقابل عنوان «circumference»، مقدار محیط را نشان میدهد. اگر محدوده انتخابی، یک چندضلعی بود، اندازه محیط در مقابل عبارت «perimeter» نمایش داده میشد. برای شکلهای نامنظم و ترکیبی، اندازه مقابل عبارت «length»، محیط شکل است.
مطالب مرتبط با این مبحث:
اندازه گیری محیط در گوگل مپ
گوگل مپ، از شناختهشدهترین ابزارهای اینترنتی برای مشاهده نقشهها و تصاویر ماهوارهای است. یکی از قابلیتهای این ابزار، تعیین محیط محدودههای روی زمین است. تصویر زیر، نمای از بالای یک زمین ورزشی را نمایش میدهد. میخواهیم محیط این زمین را توسط ابزارهای اندازهگیری گوگل به دست بیاوریم.

بر روی یکی از گوشههای زمین کلیک راست کرده و گزینه «Measure distance» را انتخاب میکنیم.

با این کار، یک نقطه بر روی نقشه نمایش داده میشود.

بر روی گوشههای دیگر میرویم و مرحله قبل را تکرار میکنیم.

در صورت نیاز میتوان با نگه داشتن کلیک چپ بر روی نقاط و کشیدن آنها، موقعیت آنها را تنظیم کرد. در انتها بر روی نقطه اول کلیک میکنیم تا محدوده بسته شود.

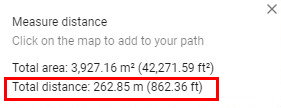
در پایین صفحه، کادری وجود دارد که اطلاعات محدوده بسته را نمایش میدهد. عدد مقابل عبارت «Total distance»، محیط زمین را نمایش میدهد.
سوالات متداول در رابطه با محیط
در این بخش، به برخی از سوالات پرتکرار در رابطه با محیط به طور خلاصه پاسخ میدهیم.
محیط یعنی چه ؟
به اندازه خط یا منحنی دور یک شکل بسته، محیط آن شکل میگویند.
واحد محیط چیست ؟
محیط با یکای طول مانند میلیمتر، سانتیمتر، متر و غیره بیان میشود.
تفاوت محیط با مساحت و حجم چیست ؟
محیط طول یا مسافت را نمایش میدهد؛ در حالیکه مساحت، بیانگر اندازه سطح (درون محیط) و حجم، نشاندهنده ظرفیت (فضای اشغال شده) است.
محیط ایران چند کیلومتر است ؟
محیط ایران برابر با ۵۸۹۴ کیلومتر است.












