زاویه داخلی و محاسبات آن در اشکال چندضلعی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در این مطلب به بحث پیرامون زوایای داخلی در شکلهای هندسی پرداخته شده است.
فیلم آموزشی زاویه داخلی در چند ضلعیها
هر یک از زوایای درونی یک شکل هندسی زاویه داخلی نامیده میشود.

مثالی از زاویه داخلی:

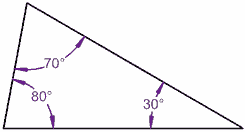
مثلث
مجموع زوایای داخلی هر مثلثی 180 درجه است. مثلث نشان دادهشده در شکل زیر را مشاهده کنید:

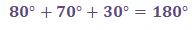
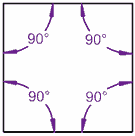
چهارضلعی (مربع و اشکال دیگر)
مجموع زوایای داخلی هر مربعی 360 درجه است. مربع نشان دادهشده در شکل زیر را مشاهده کنید:
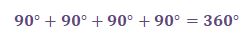
همانطور که مشاهده میکنید قضیه ذکر شده در مورد این مربع صدق میکند. اکنون یکی از اضلاع آن را به میزان 10 درجه منحرف مینماییم:


همانطور که مشاهده مینمایید هنوز هم اصل ذکر شده پابرجاست. برای اثبات شهودی این اصل، تصاویر زیر را مشاهده کنید. هر چهارضلعی را میتوان به دو مثلث تقسیم نمود.
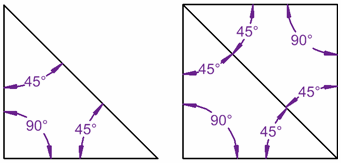
مجموع زوایای داخلی هر مثلثی 180 درجه است و چون هر چهارضلعی از دو مثلث تشکیل شده است بنابراین مجموع زوایای داخلی هر چهارضلعی برابر 360 درجه می باشد. برای مطالع بیشتر در زمینه چهارضلعیها به مطلب «چهار ضلعی ها — به زبان ساده» مراجعه کنید.
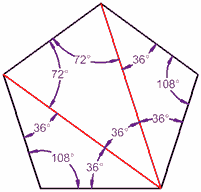
پنج ضلعی
هر پنج ضلعی دارای پنج وجه میباشد که میتوان آن را به سه مثلث تقسیم نمود بنابراین همانطور که میدانید مجموع زوایای داخلی آن 540 میباشد و زمانی که پنج ضلعی منتظم باشد (تمامی زوایا برابر باشد) هر زاویه برابر 108 = 5 / 540 میباشد.
قانون کلی
هربار که یک ضلع به هندسه موردنظرمان میافزاییم (مثلث به چهارضلعی، چهارضلعی به پنج ضلعی و ...)، به مجموع زوایای داخلی آن 180درجه افزوده میشود:
| هندسه | اضلاع | مجموع زوایای داخلی | شکل | اندازه هر زاویه |
| مثلث | 3 | 180 |  | 60 |
| چهارضلعی | 4 | 360 |  | 90 |
| پنج ضلعی | 5 | 540 |  | 108 |
| شش ضلعی | 6 | 720 |  | 120 |
| هفت ضلعی | 7 | 900 |  | 128.57 |
| هشت ضلعی | 8 | 1080 |  | 135 |
| نه ضلعی | 9 | 1260 |  | 140 |
| ... | ... | ... | ... | ... |
| nضلعی | n |  | 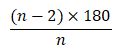 |
پس قاعده کلی به شکل زیر است:
مجموع زوایای داخلی

اندازه هر زاویه (برای یک چندضلعی منتظم)
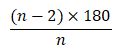
این مثال برای درک بهتر موضوع میتواند به شما کمک کند:
مثال : اندازه هر زاویه یک ده ضلعی منتظم چقدر است؟
مجموع زوایای داخلی: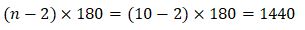
و چون هندسه موردنظر یک ده ضلعی منتظم است، اندازه هر زاویه داخلی آن:













بابا، شما را به خدا یکی راه حل پیدا کردن تعداد زوایای قائم یک هشت ضلعی رو شرح بدهههههه، لطفااااا!
اگه هشت ضلعی منتظم باشه ۸تا زاویه قائمه داره همین
هشت ضلعی شبیه چهار ضلعی استش فقط یجای چهار ضلع هشت ضلع بزن
خیلی ممنون از مقاله کاملتون
عالی و مورد استفاده
اندازه هریک از زوایای 1۶ ضلعی منتظم رو قرار بدید☹️
باسلام به همگی
برای زاویه خارجی می توان از رابطه 180 منهای ( 360 تقسیم بر تعداد اضلاع ) هم راحت بدست می آید
سلام خیلی ممنون عالی بود خیلی ازتون تشکر میکنم بابت زحمتتون
مجموع زوایای یک ۱۸ ضلعی چند درجه بیشتر از مجموع زوایای یک ۱۰ ضلعی است؟ (با راه حل)
واقعا مفید بود من تا به حال تو عمرم اینقدر از ریاضی خوشم نیومده بود ♥️♥️??
و یک چیز دیگر بگم و برم به نظر من هرچی که ریاضی رو بلد باشه براش آسونه
و هرکس که بلد نباشه براش سخته?
اندازه زاویه خارجی مثلث متساوی الضلاع چندی؟
سلام. اندازه زاویه خارجی مثلث متساویالاضلاع ۱۲۰=۶۰-۱۸۰ درجه است.
از همراهیتان با مجله فرادرس خوشحالیم.
۱۲۰=۶÷(۱۸۰×(۶-۲))
میشه اندازه هر زاویه یه ۶ ضلعی منتظم
زاویه خارجیشم میشه
۶۰=(زاویه داخلی)۱۲۰-۱۸۰
بی تی اس??☠
اندازه هر زاویه یک ۶ ضلعی منتظم چند درجه است؟???
۱۲۰=۶÷۷۲۰=(۶-۲)×۱۸۰
پس اندازه هر زاویه داخلی یه شش ضلعی ۱۲۰ درجه است
(6_2)×180=720÷6=120
اندازه هر زاویه یک ۶ ضلعی منتظم چند درجه است؟من اینو نفهمیدم?یا گفته بودید مجموع زوایای داخلی ، و یا گفته بودید مجموع زوایای خارجی?لطفا یکی راهنماییم کنه????????
120
اندازه هر ضلع ۱۲۰درجه هست شما میتونستین از مجموع زوایای داخلی که۷۲۰ درجه هست رو تقیسم بر ۶کنید میاد ۱۲۰
نمیدونم والا
دستتون درد نکند خیلی ممنون
عالی
عالی خیلی ممنون.
ببخشید متوازی الاضلاع هم ۳۶۰ هست یا ۱۸۰
اندازه هر زاویه داخلی یک هجده ضلعی منتظم چند میشه؟
۴ضلعیه دیگه
پس ۳۶۰
با درود فراوان
نوشته اید:
پنج ضلعی
هر پنج ضلعی دارای پنج وجه میباشد (است) که میتوان آن را به سه مثلث تقسیم نمود بنابراین همانطور (از این رو همانگونه)که میدانید مجموع زوایای زاویه های داخلی (درونی) آن 540 درجه میباشد (است) و زمانی که پنج ضلعی منتظم باشد (تمامی زوایا( همه زاویه ها) برابر باشد) هر زاویه برابر 108 = 5 / 540 درحه میباشد (است).
مگر نه اینکه وجه (روی) را برای جسم های هندسی بکار می بریم؟ مانند، مکعب جسمی هندسی و 6 وجهی (رویه) است.و
پس درست است بگوییم، هر پنج ضلعی پنج ضلع (پهلو) دارد.
فرهنگ سخن هم بجای ضلع واژه وجه را نوشته است.
با سپاس از کوشش های شما.
سپاس گذارم از شما که این همه مطلب خوب دارین ???دوستان منم از این سایت استفاده می کنن این سایت خیلی خوب همه چیو آموزش میده.ممنونم بابت همه چی!
اگرمجموع زوایای داخلی یکnضلعی برابر mباشد. مجموع زوایای داخلی یکn-3ضلعی چنددرجه است؟ لطفا توضیح دهید
عالی و مورد استفاده و به اندازه
عالی توضیح میدید .ممنون.بعد از سالها دوری از درس و مدرسه بدیهیات هم از ذهنم رفته بود.دراینجا به زبان ساده مرور میکنم.موفق باشید
سلام خیلی ممنون عالی بود خیلی ازتون تشکر میکنم
خیلی خوب و بهدردبخور بود
مرسی 😀
بسیار عالی با تشکر از زحمات شما