ریاضی عمومی ۱ – مفاهیم پایه به زبان ساده

ریاضی عمومی ۱ یکی از مهم‌ترین دروس پایه برای دانشجویان رشته‌های علوم پایه و مهندسی است که در آن مباحثی مانند مجموعه اعداد، مفهوم تابع، حد و پیوستگی، مشتق و کاربردهای آن، انواع انتگرال‌ شامل انتگرال معین، نامعین و ناسره در سطحی پیشرفته‌تر نسبت به دروس ریاضی در مقطع متوسطه مطرح می‌شوند. مباحث ریاضی عمومی ۱، در مباحث پیشرفته‌تری مانند ریاضی مهندسی مورد استفاده قرار می‌گیرند. این مطلب از مجله فرادرس به معرفی این مباحث اختصاص دارد و سعی شده است کلیه تعاریف، قضایا، قواعد و فرمول‌‌های مرتبط با هر بخش تا حد امکان ارائه شود.

مجموعه اعداد

اولین مبحثی که در ریاضی عمومی ۱ مطرح می‌شود، تعریف و بررسی ویژگی‌های انواع مختلف «مجموعه اعداد» (Sets of Numbers) است. کنار هم قرار گرفتن تعدادی عدد که دارای ویژگی مشترکی هستند، یک مجموعه اعداد تشکیل می‌دهد. به هر کدام از اعدادی که در یک مجموعه اعداد قرار می‌گیرند، یک عضو مجموعه گفته می‌شود. مجموعه اعداد مختلف می‌توانند تعداد اعضای متناهی یا نامتناهی داشته باشند. تمام اعضای یک مجموعه اعداد، داخل دو نماد به شکل $$\left\{ \right\}$$ قرار می‌گیرند.

در همین راستا، فیلم آموزش ریاضی عمومی ۱ – مرور و حل مساله فرادرس می‌تواند مسیر یادگیری این مبحث را برای شما هموارتر کند. لینک مشاهده این فیلم آموزشی در ادامه آورده شده است:

برای اینکه بتوانیم ویژگی‌های مشترک مجموعه‌های مختلف را بهتر تحلیل کنیم یا ببینیم چگونه می‌توان مجموعه‌ها را با هم جمع کرد، در شاخه‌ دیگری از ریاضیات به نام نظریه مجموعه‌، مفاهیمی مانند اجتماع ($$\cup$$)، اشتراک ($$\cap$$)، «نمودار ون» (Venn Diagram) و قوانین دمورگان مطرح می‌شوند. برای مثال، فرض کنید دو مجموعه عددی به شکل زیر داریم:

$$A = \left\{ 2,3,5 \right\}$$

$$B = \left\{ 4,5,6 \right\}$$

در این صورت اجتماع این دو مجموعه برابر است با مجموعه جدیدی به شکل زیر که در آن تمام اعضای دو مجموعه وجود دارند و اعضای تکراری فقط یکبار در نظر گرفته شده‌اند:

$$A \cup B = \left\{ 2,3,4,5,6\right\}$$

انواع مختلف مجموعه اعداد در ریاضی عمومی ۱ به‌صورت زیر دسته‌بندی می‌شوند:

در ادامه این بخش، به توضیح ویژگی‌ها، اعضا و نحوه نمایش هر کدام از این مجموعه‌ها می‌پردازیم.

مجموعه اعداد طبیعی

اولین مجموعه اعدادی که در ریاضی عمومی ۱ معرفی می‌شود، مجموعه اعداد طبیعی (Natural Numbers) است که با نماد $$N$$ نشان داده شده می‌شوند. مجموعه اعداد طبیعی اعدادی هستند که برای شمارش استفاده می‌کنیم، بنابراین تمام اعضای آن اعدادی مثبت هستند:

$$N = \left\{ 1,2,3,... \right\}$$

همان‌طور که ملاحظه می‌کنید، مجموعه اعداد طبیعی بی‌نهایت عضو دارد.

مجموعه اعداد کامل

با توجه به اینکه عدد صفر در شمارش استفاده نمی‌شود، پس باید دقت کنیم مجموعه اعداد طبیعی شامل عدد صفر نیست و همان‌طور که گفتیم فقط تمام اعداد مثبت را شامل می‌شود. اما اگر بخواهیم به مجموعه اعداد طبیعی عدد صفر را هم اضافه کنیم، در این صورت مجموعه اعداد کامل یا Whole Numbers را داریم که به‌صورت زیر نشان داده می‌شود:

$$\left\{ 0,1,2,3,... \right\}$$

بنابراین تمام اعضای مجموعه اعداد کامل و اعداد طبیعی مانند هم هستند، به استثنای $$0$$ که در مجموعه اعداد کامل فقط وجود دارد. به این ترتیب می‌توانیم بگوییم مجموعه اعداد طبیعی یک زیرمجموعه از مجموعه اعداد کامل است.

مجموعه اعداد صحیح

مجموعه اعداد صحیح یا Integers، شامل تمام اعداد مثبت، منفی و صفر است. اگر محور اعداد را به شکل زیر در نظر بگیریم، تمام اعدادی که در سمت چپ صفر قرار دارند، اعداد منفی و تمام اعدادی که در سمت راست صفر قرار دارند، اعداد مثبت هستند:

اگر دقت کنید، اعداد مثبت و منفی کاملا به شکل قرینه‌ای در دو سمت صفر قرار دارند. پس مجموعه اعداد صحیح که با نماد $$Z$$ نشان داده می‌شود، برابر است با:

$$Z = \left\{...,-3,-2,-1, 0,1,2,3,... \right\}$$

همچنین با توجه به تعریف مجموعه اعداد طبیعی و مجموعه اعداد کامل در بخش قبل، می‌توانیم نتیجه‌گیری کنیم که این دو مجموعه هر دو زیر مجموعه‌هایی از مجموعه اعداد صحیح محسوب می‌شوند.

مجموعه اعداد گویا

در ادامه معرفی انواع مجموعه اعداد، مجموعه اعداد گویا یا Rational Numbers را داریم که با نماد $$Q$$ نشان داده می‌شود. واقعیت این است که بین هر کدام از اعدادی که در بخش قبل روی محور اعداد صحیح مشاهده کردید، تعداد بی‌نهایت عدد دیگر وجود دارد. به عبارت دیگر، بین هر دو عدد صحیح بی‌نهایت عدد دیگر داریم که عدد صحیح محسوب نمی‌شوند، اما جزئی از مجموعه اعداد گویا هستند. مجموعه اعداد طبیعی، اعداد کامل و اعداد صحیح همگی زیرمجموعه‌هایی از مجموعه اعداد گویا محسوب می‌شوند.

یک عدد گویا عددی است که بتوان آن را به‌صورت نسبتی از دو عدد صحیح بیان کرد. به بیان دقیق‌تر هر عددی به‌صورت $$\frac{m}{n}$$ که در آن $$m, n \in Z$$ (یعنی $$m$$ و $$n$$ عضوی از مجموعه اعداد صحیح هستند)، طوری که $$n \neq 0$$، یک عدد گویا در نظر گرفته می‌شود. در واقع هر عدد گویا را می‌توانیم هم به‌صورت نسبتی از دو عدد صحیح و هم به شکل یک عدد اعشاری با تعداد ارقام اعشار متناهی یا نامتناهی (تکرار ارقام اعشار) بنویسیم. پس می‌توانیم تمام اعداد کسری و اعداد اعشاری را اعداد گویا در نظر بگیریم. تصویر زیر جایگاه چند عدد گویا را روی محور اعداد نشان می‌دهد:

اعداد اعشاری

طبق تعریفی که ریاضی عمومی ۱ برای اعداد گویا ارائه می‌دهد، می‌توانیم بگوییم تمام اعداد اعشاری عدد گویا محسوب می‌شوند، برای مثال، اعدادی مانند $$7.3$$ یا $$-1.268542$$. برای اینکه بتوانیم این اعداد را به عدد گویا تبدیل کنیم و در قالب کسر بنویسیم، کافی است ارزش مکانی آخرین رقمی را که پس از علامت اعشار قرار دارد، در نظر بگیریم.

برای مثال در مورد عدد اعشاری $$-1.268542$$، ارزش مکانی این رقم برابر است با $$1000000$$. پس شکل گویای این عدد اعشاری برابر است با:

$$-1.268542 = \frac{-1268542}{1000000}$$

همچنین می‌توانیم هر عدد گویا را به شکل یک عدد اعشاری بنویسیم و فرقی نمی‌کند که ارقام اعشار عدد اعشاری متناهی باشد یا نامتناهی. برای مثال، عدد گویای $$\frac{1}{3}$$ معادل است با عدد اعشاری $$0.3333 \ ...$$ یا $$0.\bar{3}$$. علامت بار روی عدد $$3$$، به معنای تکرار بی‌نهایت این عدد است.

اعداد گنگ

دیدیم تعریف اعداد گویا در ریاضی عمومی ۱ بر مبنای این است که بتوانیم آن‌ها را به صورت کسری از دو عدد صحیح بنویسیم. اما مجموعه‌ای از اعداد وجود دارند که این امکان در مورد آن‌ها فراهم نیست، یعنی نمی‌توانیم آن‌ها را به‌صورت نسبت دو عدد صحیح بنویسیم. این اعداد را «گنگ یا اصم» (Irrational) می‌نامیم. پس هر عددی که گویا نباشد، عدد گنگ است. دو نمونه از معروف‌ترین اعداد گنگی که قطعا در محاسبات خود زیاد با آن‌ها مواجه شده‌اید عبارت‌اند از عدد پی یا $$\pi$$ و $$\sqrt{2}$$.

مجموعه اعداد حقیقی

اگر مجموعه اعداد گویا و مجموعه اعداد گنگ را با هم جمع کنیم، به مجموعه جدیدی از اعداد به نام مجموعه اعداد حقیقی می‌رسیم که در ریاضی عمومی ۱ با نماد $$R$$ از سایر مجموعه‌ها متمایز می‌شود. مجموعه اعداد حقیقی به نوعی مجموعه مادر برای تمام مجموعه‌ها (به‌جز اعداد مختلط و موهومی) محسوب می‌شود. تمام مجموعه‌هایی که تا اینجا معرفی کردیم، زیر مجموعه‌ای از مجموعه اعداد حقیقی هستند. به بیان دقیق‌تر، هر نقطه روی محور اعدادی که در بخش‌‌های قبل دیدید، معادل است با یک عدد حقیقی.

جدول بالا مجموعه اعداد حقیقی و زیرمجموعه‌های آن را نشان می‌دهد.

مجموعه اعداد مختلط

در نهایت آخرین مجموعه‌ای که معرفی می‌کنیم، مجموعه اعداد مختلط یا Complex Numbers یا مجموعه $$C$$ است. هر عددی که بتوان آن را به فرم کلی $$a+ib$$ نوشت، یک عدد مختلط نام دارد. در این تعریف $$a$$ و $$b$$ اعداد حقیقی هستند و $$i$$ به‌صورت زیر تعریف می‌شود:

$$i = \sqrt{-1}$$

در حقیقت می‌توانیم یک عدد مختلط را مجموع دو بخش در نظر بگیریم که بخش اول آن، یک عدد حقیقی و بخش دوم یک عدد موهومی است. در ادامه توضیح می‌دهیم عدد موهومی چیست.

 عدد موهومی + عدد حقیقی = عدد مختلط

اعداد موهومی

عدد موهومی یا Imaginary Number، از حاصل‌ضرب یک عدد حقیقی در $$i$$ به‌دست می‌آید و با نماد $$I$$ نشان داده می‌شود. برای مثال اگر عدد حقیقی به‌‌صورت $$-7$$ در نظر بگیریم، عدد $$-7 i$$ قطعا یک عدد موهومی است. چنانچه $$-7 i$$ با یک عدد حقیقی جمع شود، حاصل این جمع حتما یک عدد مختلط است. یکی از مهم‌ترین کاربردهای تعریف $$i = \sqrt{-1}$$ این است که برای مثال، می‌توانیم حاصل $$\sqrt{-9}$$ را به‌صورت $$3i$$ بنویسیم. پس $$\sqrt{-9}$$ یک عدد موهومی محسوب می‌شود.

نمایش اعداد مختلط در دستگاه مختصات دکارتی و قطبی

در بخش‌های قبل با انواع مجموعه‌ اعداد آشنا شدیم و در نهایت دیدیم که کلی‌ترین مجموعه یا مجموعه مادر، مجموعه اعداد مختلط است. در این بخش می‌خواهیم توضیح دهیم اعداد مختلط را به چند روش می‌توان نمایش داد. مرسوم‌ترین دستگاه‌های مختصات برای نمایش اعداد عبارت‌اند از محور اعداد، دستگاه مختصات دکارتی، دستگاه مختصات قطبی و دستگاه مختصات کروی. با شیوه نمایش اعداد روی محور اعداد در بخش‌های قبل آشنا شدیم. نمایش عدد مختلط $$z$$ در مختصات دکارتی به‌صورت زیر است:

$$z=x+iy$$

همان‌طور که گفتیم، $$x$$ بخش حقیقی و $$y$$ بخش موهومی این عدد مختلط است. بخش حقیقی عدد مختلط روی محور افقی و بخش موهومی آن روی محور قائم در صفحه مختلط قرار می‌گیرند. برای مثال تصویر زیر نشان‌دهنده نمایش عدد مختلط $$-4-i$$ در نمایش دکارتی است:

اما اگر بخواهیم همین عدد را در قالب یک عدد و نه ترکیبی از بخش‌های حقیقی و موهومی گزارش کنیم، کافی است قدر مطلق یا اندازه عدد مختلط را محاسبه کنیم. اندازه عدد مختلط $$z=x+iy$$ که همان فاصله مختصات این نقطه از مبدا صفحه است و با $$|z|$$ نشان داده می‌شود، برابر است با:

$$|z| = \sqrt{x^2+y^2}$$

در نمایش قطبی می‌توانیم هر عدد مختلط را که معادل است با یک نقطه با مختصات مشخص در صفحه مختلط، توسط دو مولفه به نام شعاع ($$r$$) یا فاصله نقطه از مبدا و زاویه ($$\theta$$) که همان آرگومان یا زاویه بین شعاع و محور افقی است، توصیف کنیم. فرض کنید عدد مختلطی با فرم کلی $$z=x+iy$$ داریم. ارتباط بین بخش‌های حقیقی و موهومی این عدد مختلط با شعاع و زاویه‌ای که معرفی کردیم، توسط فرمول‌ها و شکل زیر مشخص می‌شود:

$$x= r \cos\theta$$

$$y= r \sin\theta$$

$$r = \sqrt{x^2+y^2}$$

بنابراین اندازه عدد مختلط با مختصاتی به شکل بالا برابر است با:

$$z= x+iy= r \cos\theta +i r \sin\theta =r( \cos\theta +i \sin\theta)$$

پس اگر بخواهیم نمایش قطبی یک عدد مختلط را به نمایش دکارتی آن تبدیل کنیم، کافی است از فرمول زیر استفاده کنیم:

$$x+iy = r(\cos \theta + i \sin \theta)$$

عکس روند بالا، یعنی تبدیل نمایش دکارتی یک عدد مختلط به نمایش قطبی آن، با فرمول‌‌های زیر انجام می‌شود:

$$r = \sqrt{x^2+y^2}$$

$$\theta = \tan^{-1}( {\frac{y}{x}})$$

نمایش دکارتی در مواردی که نیاز داریم چهار عمل اصلی یعنی جمع، تفریق، ضرب و تقسیم را روی اعداد مختلط انجام دهیم، مفید است. در این مواقع کافی است عملگرهای دو عمل اصلی جمع و تفریق روی بخش‌های حقیقی و موهومی اعداد مختلط به‌صورت جداگانه اعمال شوند. همچنین در ضرب اعداد مختلط نیز لازم است تک تک جملات در هم ضرب شوند. تقسیم اعداد مختلط با ضرب و تقسیم کردن کسر حاصل در مزدوج مخرج حل می‌شود.

قضیه دموآور

پس از اینکه آموختیم چگونه می‌توان اعداد مختلط را در ریاضی عمومی ۱ در دستگاه مختصات قطبی نمایش داد، حالا نوبت به این می‌رسد که یاد بگیریم چگونه عملگرهای مختلفی مانند جمع یا ضرب روی این اعداد عمل می‌کنند. ابتدا فرمول‌هایی را در این راستا معرفی می‌کنیم که اولین بار توسط ریاضیدان فرانسوی به نام «آبراهم دموآور» (Abraham de Moivre) مطرح شد. یادگیری این فرمول‌ها به شما کمک می‌کند تا با اعداد مختلط در نمایش قطبی راحت‌تر کار کنید. فرض کنید دو عدد مختلط به شکل زیر داریم:

$$z_1= r_1( \cos \theta_1 +i \sin \theta_1)$$

$$z_2= r_2( \cos \theta_2 +i \sin \theta_2)$$

در این صورت حاصل‌ضرب این دو عدد برابر است با:

$$z_1z_2= r_1r_2[ \cos (\theta_1+\theta_2) +i \sin (\theta_1+\theta_2)]$$

همچنین حاصل‌ تقسیم این دو عدد نیز به‌ شکل زیر محاسبه خواهد شد:

$$\frac{z_1}{z_2}= \frac{r_1}{r_2}[ \cos (\theta_1-\theta_2) +i \sin (\theta_1-\theta_2)] , z_2\neq 0$$

قضیه دموآور به منظور ساده‌سازی روند پیدا کردن توان‌های اعداد مختلط در نمایش قطبی بکار می‌رود. طبق این قضیه، اگر توان $$‌n$$ در عدد مختلط توان‌داری به شکل $$‌z^n$$ یک عدد صحیح و مثبت باشد، در این صورت حاصل این عدد توانی برابر است با توان $$‌n$$ام شعاع $$‌r$$ و آرگومان‌هایی که $$‌n$$ برابر شده‌اند:

$$‌z^n = r^n ( \cos n\theta +i \sin n\theta)$$

قضیه ریشه nام

موضوع قضیه ریشه $$‌n$$ام در ریاضی عمومی ۱ یافتن ریشه‌های اعداد مختلط در نمایش قطبی است. این قضیه که در حقیقت زیرمجموعه‌ای از قضیه دموآور محسوب می‌شود، بیان می‌کند $$‌n$$امین ریشه  از یک عدد مختلط در نمایش قطبی به شکل زیر به‌دست می‌آید:

$$‌z^{\frac{1}{n}} = r^{\frac{1}{n}} [\cos (\frac{\theta}{n}+\frac{2k\pi}{n} )+i \sin (\frac{\theta}{n}+\frac{2k\pi}{n} )]$$

در این رابطه $$k = 0,1,2,3, ...,n-1$$ است. همچنین $$‌\frac{2k\pi}{n}$$ به $$‌\frac{\theta}{n}$$ اضافه شده است تا ریشه‌های تناوبی در این محاسبات در نظر گرفته شوند.

چگونه ریاضی عمومی ۱ را با فرادرس بهتر یاد بگیریم؟

در این بخش قصد داریم چند دوره آموزشی از مجموعه فرادرس را با موضوع ریاضی عمومی ۱ و مباحث مطرح شده در آن، به شما معرفی کنیم. مشاهده این فیلم‌های آموزشی به شما کمک می‌کند تا یادگیری خود را در این زمینه تکمیل کنید، به‌ویژه اینکه دسترسی برخی از این فیلم‌ها ‌به‌صورت رایگان است و در هر کدام روی یک مبحث خاص تمرکز شده است تا بتوانید با تمرین و توضیح بیشتر، کاملا به آن بخش تسلط پیدا کنید:

1. فیلم آموزش ریاضی عمومی ۱ – مرور و حل مساله فرادرس
2. فیلم آموزش ریاضی عمومی ۱ + مرور و حل تست کنکور کارشناسی ارشد فرادرس
3. فیلم آموزش رایگان حد و پیوستگی ریاضی عمومی ۱ + مثال‌های کاربردی فرادرس
4. فیلم آموزش رایگان قضیه فشردگی یا ساندویچ + مثال‌های کاربردی فرادرس
5. فیلم آموزش رایگان روابط اساسی مشتق + حل مثال فرادرس
6. فیلم آموزش رایگان مشتق پارامتری و زنجیری + حل مثال فرادرس
7. فیلم آموزش رایگان روش حل مشتق ضمنی + حل مثال‌‎‌های مختلف فرادرس
8. فیلم آموزش رایگان روش حل انتگرال تغییر متغیر + به زبان ساده با مثال فرادرس

مفهوم تابع

در بخش قبل یاد گرفتیم مجموعه اعداد چیست و با مهم‌ترین مجموعه اعداد در ریاضی عمومی ۱ آشنا شدیم. در این بخش می‌خواهیم ببینیم چگونه می‌شود بین مجموعه‌‌های مختلف ارتباط برقرار کرد. تابع ابزاری است که به کمک آن می‌توانیم مجموعه‌ شماره یک یعنی مجموعه $$a,b,c$$ در تصویر زیر را به مجموعه شماره دو یا $$x,y,z$$ ربط دهیم. مجموعه اول دامنه یا Domain و مجموعه دوم برد یا Range تابع نامیده می‌شود.

دامنه و برد تابع

وزن نوزادی را فرض کنید که همراه با زمان در حال تغییر است و قصد دارید این تغییرات را توسط یک نمودار نمایش داده و سپس تحلیل کنید. اگر نمودار وزن بر حسب زمان را رسم کنید، در حقیقت نمودار تابعی را رسم کرده‌اید که طبق آن، وزن با زمان تغییر می‌کند. در این مثال، زمان مجموعه اول یا دامنه این تابع و وزن نوزاد، مجموعه دوم یا برد تابع است. بنابراین می‌توانیم تابع را مجموعه‌ای در نظر بگیریم که اعضای آن جفت‌ اعداداند، به گونه‌ای که ترتیب قرار گرفتن هر دو عدد جفت شده مهم است. در مثالی دیگر، تابعی را در نظر بگیرید که با مجموعه‌ای به شکل زیر توصیف شده است. اگر دقت کنید، رابطه بین عدد اول و دوم در هر جفت عدد به این صورت است که عدد دوم، دو برابر عدد اول است:

$$\left\{ (1,2),(2,4),(3,6),(4,8),(5,10)\right\}$$

در این تابع مجموعه اعداد دامنه برابر است با:

$$\left\{ 1,2,3,4,5\right\}$$

و برد نیز به شکل زیر است:

$$\left\{ 2,4,6,8,10\right\}$$

هر کدام از اعضای دامنه در واقع همان ورودی تابع هستند. ورودی تابع مقادیر مستقل در تابع هستند که عموما با $$x$$ نمایش داده می‌شوند. در حالی که مقادیر خروجی یا برد تابع مقادیر وابسته‌اند و با $$y$$ نشان داده می‌شوند. بنابراین تابعی مانند $$f$$، هر عضو از مجموعه دامنه را به یک عضو از مجموعه برد ربط می‌دهد. نکته مهمی که در تشخیص تابع باید به آن دقت کنیم این است که مقادیر دامنه یا $$x$$ نباید تکراری باشند. به مثال‌هایی که در تصویر زیر نشان داده شده است، توجه کنید:

در اولین تصویر از سمت راست، دو مقدار $$y$$ و $$z$$ در مجموعه برد، به یک مقدار از دامنه یعنی $$q$$ متناظر شده‌اند. چنین چیزی مطابق تعریف تابع نیست. اما عکس آن، ممکن است. در تصویر (a) دو مقدار $$q$$ و $$r$$ در دامنه هر دو با یک مقدار از برد یعنی $$n$$ متناظر شده‌اند. بنابراین اگر بخواهیم ببینیم آیا رابطه بین هر دو مجموعه‌ای که به ما داده می‌شود، تابع محسوب می‌شود یا نه، بهتر است به روش زیر عمل کنیم:

• مشخص کردن دامنه یا ورودی تابع
• مشخص کردن برد یا خروجی تابع
• اگر هر ورودی فقط و فقط به یک خروجی مربوط شود، تابع داریم.
• اگر ورودی داشته باشیم که به دو یا تعداد بیشتری از خروجی‌ها مربوط باشد، تابع نداریم.

نمودار تابع

پس از اینکه با مفهوم تابع، دامنه و برد در ریاضی عمومی ۱ آشنا شدیم، می‌خواهیم ببینیم چگونه می‌توان تابع را به زبان ریاضی نمایش داد. برای نشان دادن هر تابعی مانند $$f$$ با دامنه $$x$$ و برد $$y$$، به‌صورت زیر عمل می‌کنیم:

$$y = f (x)$$

روش‌های دیگر نمایش تابع، استفاده از جدول یا رسم نمودار تابع است. نمودار یک تابع، مجموعه نقاطی به‌صورت $$(x,y)$$ در صفحه هستند که در معادله $$y = f(x)$$ صدق می‌کنند. در همین راستا، یکی از آسان‌ترین روش‌های تست تابع بودن یک نمودار این است که خط عمودی روی آن رسم کنیم. اگر رسم خط عمودی در هر بخش از نموداری، آن را در دو یا تعداد بیشتری از دو نقطه قطع کند، آن نمودار توصیف کننده یک تابع نیست. شکل زیر را در نظر بگیرید:

در اولین نمودار از سمت راست و نمودار وسطی، خطوط عمودی در دو نقطه نمودار را قطع کرده‌اند. این بدین معنا است که یک ورودی با دو خروجی متناظر شده است و همان‌طور که توضیح دادیم، تعریف تابع این نیست.

انواع تابع

یکی دیگر از مباحث مربوط به ریاضی عمومی ۱، دسته‌بندی انواع مختلف توابع بر اساس ویژگی‌های آن‌ها است. معروف‌ترین و پرکاربردترین توابع ریاضیاتی عبارت‌اند از:

• تابع یک به یک
• تابع ثابت
• تابع خطی یا همانی
• تابع مربعی یا درجه دو
• تابع مکعبی یا درجه سه
• تابع قدر مطلق
• تابع رادیکالی
• تابع نمایی
• تابع مثلثاتی
• تابع لگاریتمی
• تابع جزء صحیح یا پله‌ای

به جهت گستردگی موضوع انواع تابع و ويژگی‌های آن‌ها، در بخش‌های بعد تنها به توضیح برخی از این توابع همراه با رسم نمودار و فرمول توصیف کننده آن‌ها خواهیم پرداخت. اما اگر تمایل دارید با ویژگی‌های انواع توابع بیشتر آشنا شوید، می‌توانید به مطلبی که در انتهای این بخش لینک آن قرار داده شده است، مراجعه کنید. همچنین اگر علاقه‌مند هستید تا مراحل رسم نمودار توابع مثلثاتی سینوس و کسینوس را بیاموزید، مطالعه مطلب «رسم نمودار سینوس و کسینوس – به زبان ساده با مثال و تمرین» از مجله فرادرس می‌تواند راهنمای بسیار خوبی برای شما در این زمینه باشد. یادگیری مشخصات انواع توابع در حل مسائل مشتق‌گیری، حدگیری و انتگرال‌گیری بسیار مفید است.

تابع یک به یک

اگر مجددا به شکلی که در بخش دامنه و برد توضیح دادیم، دقت کنید، تصویر (b) یک تابع یک به یک محسوب می‌شود، در حالی که تصویر (a) نشان دهنده یک تابع یک به یک نیست. در واقع اگر در تابعی خروجی با دو یا تعداد بیشتری ورودی متناظر شود، در این صورت می‌گوییم این تابع یک به یک نیست. در توابع یک به یک هر خروجی فقط و فقط با یک ورودی متناظر است.

برای مثال، اگر مساحت یک دایره را به‌عنوان تابعی از شعاع آن در نظر بگیریم، آیا این تابع یک تابع یک به یک است؟ پاسخ مثبت است. چون تغییرات مساحت با شعاع به شکل زیر است:

$$f(r) = \pi r^2$$

تابع مساحت دایره، یک تابع مشخص و متمایز است، به این معنا که برای هر مقدار از $$r$$ یک مساحت متمایز داریم. پس برای هر ورودی، یک خروجی وجود دارد و یک به یک بودن برقرار است. مشابه آزمون خط عمودی که برای مشخص کردن تابع بودن یا تابع نبودن یک نمودار معرفی شد، در این بخش هم آزمون مشابهی به نام آزمون خط افقی داریم تا بتوانیم یک به یک بودن یک تابع را تعیین کنیم. اگر هر گونه خط افقی و موازی با محور افقی که روی نمودار تابع رسم می‌کنیم، آن را در بیش از یک نقطه قطع کند، در این صورت آن تابع یک به یک نیست. به‌عنوان مثال، نمودار زیر طبق آزمون خط عمودی نمودار یک تابع محسوب می‌شود، اما این تابع یک به یک نیست، چون خط افقی وجود دارد که آن را در دو نقطه قطع کرده است:

تابع ثابت

تابع ثابت همان‌طور که از نامش مشخص است، به تابعی گفته می‌شود که به ازای تمام مقادیر ورودی، همواره خروجی برابر با یک عدد ثابت است. پس برد یک تابع ثابت همیشه دارای یک عضو است و این مقدار بر اساس ورودی تغییر نمی‌کند. به این ترتیب نمودار تابع ثابت، همواره یک خط راست و موازی با محور افقی است. اینکه این خط، متناظر با چه مقداری از $$y$$ است، توسط معادله تابع مشخص می‌شود:

$$y = f(x) = constant$$

تصویر بالا، نمونه‌ای از یک تابع ثابت با فرمول $$f(x) = 2$$ را نشان می‌دهد. همان‌طور که در جدول مقادیر مشخص است، با تغییر $$x$$، برد تابع یعنی $$f(x)$$ همواره ثابت و برابر با $$2$$ است.

تابع خطی، درجه دو و درجه سه

نوع دوم از انواع توابع که در ریاضی عمومی ۱ معرفی می‌کنیم، توابعی هستند که در آن‌ها تغییرات خروجی با ورودی به صورت خطی (درجه یک یا همانی)، درجه دو یا مربعی، درجه سه یا مکعبی است. اگر یک عبارت جبری بر حسب $$x$$، فقط شامل توان‌های اول از $$x$$ باشد، می‌گوییم این عبارت خطی یا درجه یک است. اما اگر چنین عبارتی شامل توان‌های دوم از $$x$$ هم باشد، می‌گوییم عبارت جبری ما درجه دو است و به همین ترتیب برای توان‌های بالاتر. بنابراین تابع خطی فرمولی به‌ شکل زیر دارد:

$$y = f(x) = ax+b$$

در این فرمول $$a$$ و $$b$$ اعداد ثابت هستند. برای مثال، نمودار زیر یک تابع خطی را نشان می‌دهد که در آن $$a = 1$$ و $$b = 0$$ است. چنین تابعی از مبدا مختصات عبور می‌کند و در آن همواره مقادیر $$x$$ و $$y$$ برابر هستند. به بیان دقیق‌تر، در این نوع تابع دامنه و برد با هم برابر هستند، به همین علت آن را تابع همانی هم نام‌گذاری می‌کنند.

اما ممکن است معادله جبری تابع، شامل توان‌های بالاتری از $$x$$ مانند توان دوم و سوم و ... هم باشد. در این صورت چنین تابعی خطی محسوب نمی‌شود و نام‌گذاری آن بر اساس بالاترین توانی از $$x$$ که در معادله جبری تابع دیده می‌شود، انجام خواهد شد. به این ترتیب فرمول کلی تابع درجه دو به شکل زیر است:

$$y = f(x) =ax^2 + bx+ c$$

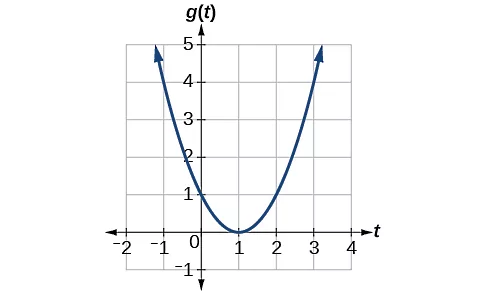
اگر در این فرمول فرض شود که $$a = 1$$ و $$b = c = 0$$ است، در این صورت فرمول و نمودار تابع درجه دوم ما به شکل زیر خواهد شد:

$$y = f(x) =x^2$$

همچنین فرمول کلی برای یک تابع جبری از درجه سوم به شکل زیر است:

$$y = f(x) =dx^3+ax^2 + bx+ c$$

که با در نظر گرفتن ثوابتی به شکل $$d = 1$$ و $$a= b = c = 0$$، نمودار آن به این صورت خواهد شد:

تابع قدر مطلق

اگر با مفهوم قدر مطلق آشنا باشید، می‌دانید که قدر مطلق هر عددی مانند $$-a$$ به صورت $$|-a|$$ نشان داده می‌شود و همواره برابر است با $$a$$:

$$|-a| = |a| = a$$

تابع قدر مطلق در ریاضی عمومی ۱ نیز بر همین اساس تعریف می‌شود. اگر فرمول تابع قدر مطلق به شکل زیر باشد، با در نظر گرفتن مقادیری مانند $$-2$$، $$0$$ و $$2$$ برای $$x$$، مقادیر $$y$$ این تابع طبق جدول زیر به‌دست خواهد آمد:

$$y = f(x) =|x|$$

تابع رادیکالی

یکی دیگر از مهم‌ترین توابع در ریاضی عمومی ۱، توابع رادیکالی هستند. در این بخش به ساده‌ترین نوع این تابع، یعنی تابعی به شکل $$y = f(x) =\sqrt{x}$$ می‌پردازیم. اگر برای مقادیر ورودی این تابع مطابق جدول زیر، $$0$$، $$1$$ و $$2$$ را انتخاب کنیم، با محاسبه رادیکال این مقادیر، خروجی تابع به‌دست می‌آید و در نتیجه مقادیر $$y$$ بر حسب $$x$$ به‌ شکل زیر رسم می‌شوند:

در مورد توابع رادیکالی نکته مهمی که وجود دارد مقادیر مجاز ورودی یا دامنه است. همان‌طور که در جدول‌های بالا و پایین مشاهده می‌کنید، مقادیر زیر رادیکال هیچ‌گاه نمی‌توانند منفی باشند. همچنین توابع رادیکالی می‌توانند فرجه‌های متفاوتی داشته باشند. نمودار بالا شکل یک تابع رادیکالی با فرجه $$2$$ بود، اما نمودار زیر یک تابع رادیکالی با عبارت مشابه زیر رادیکال اما با فرجه $$3$$ را نشان می‌دهد:

ترکیب توابع

یکی از روش‌های ایجاد یک تابع جدید این است که دو یا چند تابع را با هم ترکیب کنیم. فرآیند ترکیب توابع، به گونه‌ای که خروجی یک تابع با ورودی تابع دیگر برابر شود را ترکیب توابع می‌نامیم و به‌صورت زیر نشان می‌دهیم:

$$fog(x) = f(g(x))$$

پس سمت چپ این رابطه به‌صورت ترکیب تابع $$f$$ با $$g$$ در $$x$$ خوانده می‌شود. در حالت کلی، $$fog(x)$$ با $$gof(x)$$ برابر نیست.

متوسط نرخ تغییرات یک تابع

یکی دیگر از مهم‌ترین ویژگی‌های یک تابع، روند تغییرات آن و در نتیجه‌، صعودی یا نزولی بودن آن است. دانستن این مفهوم ریاضی عمومی ۱ در محاسبه مشتق‌های اول و دوم یک تابع بسیار کمک کننده است. در این بخش ابتدا نشان می‌دهیم چگونه می‌توانیم متوسط نرخ تغییرات یک تابع را پیدا کنیم. سپس توضیح می‌دهیم چگونه می‌توان با بررسی نمودار یک تابع مشخص کرد که آیا این تابع در حال افزایش است یا کاهش. همچنین در ادامه به نحوه تعیین نقاطی با بیشترین یا کمترین مقادیر خواهیم پرداخت. منظور ما از متوسط نرخ تغییرات یک تابع در ریاضی عمومی ۱، تغییرات خروجی آن تابع نسبت به تغییرات ورودی آن است. اگر مقادیر ورودی و خروجی را به ترتیب به‌صورت $$x$$ و $$y = f(x)$$ در نظر بگیریم، متوسط نرخ تغییرات برابر است با:

$$\frac{f(x_2)-f(x_1)}{x_2-x_1} = \frac{y_2-y_1}{x_2-x_1} = \frac{\triangle y}{\triangle x}$$

نماد مهمی که برای نشان دادن تغییرات به‌کار می‌رود، حرف یونانی $$\triangle$$ است. پس اگر مقادیر یک تابع را در نقاط مختلف داشته باشیم یا بتوانیم این مقادیر را محاسبه کنیم، برای یک بازه مشخص از مقادیر $$x$$ می‌توانیم متوسط نرخ تغییرات تابع را به شیوه بالا به‌دست آوریم. همچنین گاهی ممکن است نمودار تابع را در اختیار داشته باشیم و با توجه به آن بتوانیم این متوسط را حساب کنیم. به مثال زیر توجه کنید:

فرض کنید تابع $$g(t)$$ نموداری به شکل بالا دارد و می‌خواهیم متوسط نرخ تغییرات آن را در بازه $$[-1,2]$$ پیدا کنیم. برای اینکه فرمول بالا را استفاده کنیم، اولین قدم این است که مختصات نقاط ابتدا و انتهای بازه خواسته شده را دقیقا مشخص کنیم. در ابتدای بازه، $$x= -1$$ است و مقدار تابع در این ورودی طبق شکل برابر است با $$g(-1)= 4$$. نقطه انتهای بازه داده شده برابر است با $$x= 2$$ که مقدار $$y$$ متناظر با آن می‌شود $$g(2)= 1$$.

حالا طبق فرمول داده شده عمل می‌کنیم تا متوسط نرخ تغییرات به‌دست آید:

$$\frac{\triangle y}{\triangle x}= \frac{g(x_2)-g(x_1)}{x_2-x_1} = \frac{1-4}{2-(-1)} =\frac{-3}{3} =-1$$

اگر دقت کنید، ترتیبی که نقاط را در فرمول قرار می‌دهیم، حائز اهمیت است.

صعودی یا نزولی بودن تابع

صعودی یا نزولی بودن یک تابع را می‌توانیم از روی نمودار آن تعیین کنیم. اگر تابعی در یک بازه مشخص روند افزایشی داشته باشد، به این معنا که مقادیر $$y = f(x)$$ آن همراه با افزایش $$x$$ زیاد شوند، در این صورت می‌گوییم این تابع یک تابع صعودی است. اما اگر مقادیر $$y = f(x)$$ تابعی در یک بازه مشخص همزمان با افزایش $$x$$ کم شوند، در این صورت این تابع یک تابع نزولی محسوب می‌شود. بنابراین با توجه به مبحث بخش قبل، می‌توانیم بگوییم متوسط نرخ تغییرات برای یک تابع صعودی همواره مثبت است، در حالی که برای یک تابع نزولی، این مقدار همواره منفی است.

شکل بالا این توضیحات را روی نمودار یک تابع فرضی نشان می‌دهد. مورد خاصی داریم که در آن متوسط نرخ تغییرات تابع برابر با صفر است، یعنی همزمان با افزایش مقادیر $$x$$، مقادیر $$y = f(x)$$ تابع تغییری نمی‌کند و همواره ثابت می‌ماند، در این حالت تابع نه نزولی است و نه صعودی.

جدول بالا نشان می‌دهد روند تغییرات برخی از انواع توابعی که معرفی کردیم، به چه صورت است.

اکسترمم نسبی یا اکسترمم محلی

بررسی صعودی یا نزولی بودن یک تابع در بازه‌های مختلف به ما کمک می‌کند تا بتوانیم نقاط اکسترمم محلی آن تابع را تعیین کنیم. نقطه‌ای که در آن تغییرات تابع از حالت صعودی به نزولی تغییر می‌کند، ماکزیمم یا بیشینه محلی نامیده می‌شود. اگر در نقطه‌ای روند تغییرات تابع از نزولی به صعودی تغییر کند، در این صورت این نقطه مینیمم یا کمینه محلی است.

برای یک تابع فرضی ممکن است در بازه‌های مختلف روند تغییرات نمودار صعودی یا نزولی باشد، بنابراین بخش‌های صعودی و نزولی آن به هم تبدیل می‌شوند و در نتیجه ممکن است چند نقطه ماکزیمم یا مینیمم محلی یا به‌طور کلی چند نقطه اکسترمم محلی داشته باشیم. نکته مهم در مورد نقاط اکسترمم محلی این است که این نقاط فقط در بازه مشخصی که بخشی از کل دامنه تابع است، اکسترمم محسوب می‌شوند. برای مثال، در مورد نمودار تابعی که در بخش قبل دیدیم، دو نقطه اکسترمم محلی داریم:

نقطه‌ای با مختصات $$(-2, 16)$$ معادل مینیمم محلی و نقطه $$(2, -16)$$ معادل است با ماکزیمم محلی برای این تابع. بنابراین تابعی مانند $$f$$ زمانی دارای یک ماکزیمم محلی در نقطه $$b$$ از بازه باز $$(a,c)$$ است که همواره برای هر $$x$$ مقدار $$f(b)$$ بزرگتر یا مساوی $$f(x)$$ باشد. به عکس، تابعی مانند $$f$$ زمانی دارای یک مینیمم محلی در نقطه $$b$$ از بازه باز $$(a,c)$$ است که همواره برای هر $$x$$ مقدار $$f(b)$$ کوچکتر یا مساوی $$f(x)$$ باشد.

به مثال زیر توجه کنید. می‌خواهیم تمام نقاط ماکزیمم و مینیمم تابع زیر را در بازه نشان داده شده در شکل پیدا کنیم. در نقطه‌ای با مختصات $$(1,2)$$، روند تغییرات نمودار از صعودی به نزولی تغییر می‌کند. پس این نقطه معادل است با یک اکسترمم یا به بیان دقیق‌تر، یک ماکزیمم محلی. همچنین در نقطه $$(-1,-2)$$ نیز تغییرات نمودار را از حالت نزولی به صعودی داریم. پس این نقطه هم معادل می‌شود با یک مینیمم محلی.

به نقطه $$(0,0)$$ دقت کنید. در این نقطه نمودار در حالت صعودی باقی ‌می‌ماند. پس این نقطه یک اکسترمم محسوب نمی‌شود. در بخش‌های بعد راجع‌به ویژگی‌های این نقطه صحبت خواهیم کرد.

نظریه مقدار حدی و اکسترمم مطلق

در بخش‌های قبل اشاره کردیم که پیدا کردن نقاطی با بیشترین یا کمترین مقادیر برای یک تابع ممکن است در ناحیه مشخصی از یک بازه باز انجام شود یا در کل دامنه تابع. اگر موقعیت اول را بررسی کنیم، اکسترمم‌های محلی را برای یک تابع در ریاضی عمومی ۱ مشخص کرده‌ایم اما اگر کل دامنه تابع را در نظر بگیریم، اکسترمم مطلق تابع را تعیین کرده‌ایم. به این ترتیب بیشترین مقدار تابع در کل دامنه آن معادل است با ماکزیمم مطلق و کمترین مقدار تابع در دامنه می‌شود مینیمم مطلق آن.

برای نمونه، تابعی به شکل بالا را در نظر بگیرید که در آن تشخیص نقاط ماکزیمم و مینیمم مطلق واضح است. برخلاف نمودار توابعی که در بخش قبل داشتیم (ابتدا و انتهای توابع با علامت پیکان در شکل به معنای بی‌نهایت مشخص شده بود)، در اینجا نقاط ابتدایی و انتهایی دامنه مشخص هستند. بنابراین می‌توانیم تعاریف زیر را برای اکسترمم‌های مطلق تابعی مانند $$f$$ در نظر بگیریم:

• ماکزیمم مطلق تابعی مانند $$f$$ در نقطه‌ای مانند $$x= c$$ برابر است با $$f(c)$$، اگر برای تمام مقادیر $$x$$ در دامنه $$f$$ همواره داشته باشیم $$f(c)\geq f(x)$$.
• مینیمم مطلق تابعی مانند $$f$$ در نقطه‌ای مانند $$x= c$$ برابر است با $$f(c)$$، اگر برای تمام مقادیر $$x$$ در دامنه $$f$$ همواره داشته باشیم $$f(c)\leq f(x)$$.

در همین زمینه قضیه‌ای با عنوان نظریه مقدار حدی یا Extreme Value Theorem داریم که به تعریف دقیق‌تر اکسترمم‌ مطلق یک تابع می‌پردازد. در این نظریه فرض می‌شود اگر تابع $$f$$ روی بازه بسته‌ای به شکل $$[a,b]$$ پیوسته باشد، در این صورت نقطه‌ای در این بازه وجود دارد، به گونه‌ای که تابع $$f$$ در آن نقطه یک ماکزیمم مطلق دارد و نقطه دیگری هم در همین بازه داریم، طوری که تابع $$f$$ در آن یک مینیمم مطلق داشته باشد.

انواع تقارن در نمودار توابع

یکی دیگر از مهم‌ترین مفاهیم در مورد توابع مختلف این است که بتوانیم تقارن در آن‌ها را تشخیص دهیم. یکی از آسان‌ترین روش‌های تشخیص نوع تقارن توابع، توجه به نمودار آن‌ها است. به‌طور کلی در ریاضی عمومی ۱ سه نوع تقارن برای توابع تعریف می‌شود:

• تقارن نسبت به محور yها
• تقارن نسبت به محور xها
• تقارن نسبت به مبدا مختصات

تقارن تابع نسبت به محور قائم یا محور yها به این صورت است که برای هر نقطه‌ای مانند $$(a,b)$$ روی نمودار تابع، نقطه‌ متناظری با مختصات $$(-a,b)$$ وجود دارد، به گونه‌ای که داریم:

$$f(x,y)= f(-x,y)$$

در این نوع تقارن محور قائم مانند یک آینه برای نمودار تابع عمل می‌کند. در مقابل، تقارن نسبت به محور افقی یا محور xها را داریم که در آن برای هر نقطه‌ای مانند $$(a,b)$$، نقطه متناظری به‌صورت $$(a,-b)$$ روی نمودار تابع وجود دارد. به عبارت دیگر، برای یک تابع متقارن نسبت به محور x همواره این رابطه صادق است:

$$f(x,y)= f(x,-y)$$

اگر تابعی نسبت به محور xها متقارن باشد، محور افقی مانند آینه‌ای برای نمودار آن عمل می‌کند. اما در تقارن یک تابع نسبت به مبدا، باید رابطه زیر برای هر نقطه از نمودار تابع برقرار باشد:

$$f(x,y)= f(-x,-y)$$

توابع زوج و فرد

یادگیری مفهوم تقارن در توابع، به ما کمک می‌کند تا بتوانیم تشخیص دهیم کدام تابع زوج است و کدام فرد. طبق تعریف، اگر برای تابعی $$f(x)= f(-x)$$ برقرار باشد، می‌گوییم آن تابع زوج است. به عبارت دیگر، توابع زوج نسبت به محور قائم متقارن‌اند. تمام توابع توانی شامل توان‌های زوج $$x$$ مانند $$x^2$$ و $$x^8$$ یا تابع مثلثاتی کسینوس، زوج هستند.

از طرفی، اگر با منفی شدن $$x$$، داشته باشیم $$f(-x)= -f(x)$$، در این صورت تابع $$f$$ یک تابع فرد است. تمام توابع توانی شامل توان‌های فرد $$x$$ مانند $$x^3$$ و $$x^5$$ و تابع مثلثاتی سینوس، فرد هستند.

تابع معکوس

آخرین مبحثی که در بخش توابع از ریاضی عمومی ۱ توضیح می‌دهیم، تابع معکوس است. اهمیت نحوه محاسبه تابع معکوس یا معکوس یک تابع، در بخش مشتق‌‌گیری و حل انتگرال‌ها بیشتر مشخص می‌شود. تابعی مانند $$g(x)$$، معکوس تابع $$f(x)$$ نامیده می‌شود اگر همواره داشته باشیم:

$$f(g(x))=g(f(x) = x$$

عموما معکوس تابع $$f(x)$$ را با $$f^{-1}(x)$$ نشان می‌دهند. در ادامه با حل مثال نشان می‌دهیم مراحل محاسبه معکوس یک تابع به چه صورت است. فرض کنید می‌خواهید معکوس تابع زیر را پیدا کنید:

$$f(x) = y = 3x^3-5$$

اولین قدم این است که جای متغیرها را عوض کنیم، یعنی $$y = 3x^3-5$$ می‌شود $$x = 3y^3-5$$. در نتیجه داریم:

$$x +5 = 3y^3 \Rightarrow \frac{x+5}{3} = y^3$$

$$\Rightarrow [\frac{x+5}{3}]^{\frac{1}{3}} = y$$

$$\Rightarrow f^{-1}(x) = y = [\frac{x+5}{3}]^{\frac{1}{3}}$$

حد و پیوستگی

پس از اینکه یاد گرفتیم مفهوم تابع در ریاضی عمومی ۱ چیست، حالا می‌توانیم مبحث حد و پیوستگی را شروع کنیم. فرض کنید تابعی به شکل $$f(x)$$ داریم و ورودی آن یعنی $$x$$ را تا مقدار ثابت $$a$$ افزایش می‌دهیم. چنانچه در این فرآیند خروجی این تابع یعنی $$f(x)$$ نیز به مقدار مشخصی مانند $$L$$ نزدیک شود، در این صورت می‌گوییم حد یا لیمیت تابع $$f(x)$$ وقتی $$x$$ به سمت $$a$$ میل می‌کند برابر است با $$L$$. این توضیحات به‌صورت خلاصه و به کمک ریاضیات به شکل زیر نشان داده می‌شود:

$$\lim_{x \rightarrow a} f(x) = L$$

حدگیری یکی از ضروری‌ترین ابزارهای مطالعه و تحلیل در ریاضی عمومی ۱ محسوب می‌شود که پیش زمینه یادگیری آن، آشنایی با مفهوم تابع و کاربرد آن در بررسی پیوستگی توابع، مشتق‌گیری و محاسبه انواع انتگرال‌ها است. برای مثال، تابعی به شکل $$f(x) = \frac{x^2 - 1 }{x - 1}$$ را در نظر بگیرید. از توضیحاتی که در مورد دامنه تابع دادیم، می‌توان نتیجه گرفت که در اینجا $$x = 1$$ جزء دامنه این تابع نیست. با این وجود، می‌خواهیم ببینیم این تابع دقیقا در نزدیکی نقطه $$x = 1$$ یا در همسایگی آن چه رفتاری دارد.

اولین قدم این است که جدولی از مقادیر به‌صورت زیر در نظر بگیریم. همان‌طور که ملاحظه می‌کنید، شش نقطه مختلف برای مقداردهی به $$x$$ انتخاب کرده‌ایم، به‌گونه‌ای که سه نقطه کمی کوچکتر از $$x = 1$$ و سه نقطه کمی بزرگتر از $$x = 1$$هستند. به عبارت دیگر، نقاط حول نقطه $$x = 1$$ یا همسایگی آن را انتخاب کرده‌ایم تا بتوانیم تحلیل درستی از رفتار تابع حول این نقطه داشته باشیم. با قرار دادن هر کدام از این مقادیر به‌جای $$x$$، خروجی یا $$f(x)$$ متناظر به‌صورت زیر به‌دست خواهد آمد:

با دقت در مقادیر $$f(x)$$ می‌توانیم به این نتیجه برسیم که همزمان با افزایش مقادیر $$x$$ تا نزدیکی مقدار $$1$$، مقادیر $$f(x)$$ متناظر به عدد $$2$$ نزدیک می‌شوند. بنابراین اگر مقادیر $$x$$ به اندازه کافی به $$1$$ نزدیک شوند، حد تابع $$f(x)$$ برابر است با $$2$$:

$$\lim_{x \rightarrow 1} f(x) = 2$$

نکته: در تعریف حد به شکل $$\lim_{x \rightarrow a} f(x) = L$$، لازم است مقادیر $$x$$ به اندازه کافی به $$a$$ نزدیک شوند. جهت نزدیک شدن مقادیر $$x$$ به $$a$$ می‌تواند از سمت مقادیر کمتر یا بیشتر از $$a$$ باشد. اما $$x$$ هیچ گاه با $$a$$ برابر نمی‌شود. بنابراین همان‌طور که در مثال بالا دیدید، در تعریف حد عددی که مقادیر $$x$$ به سمت آن میل می‌کنند، ممکن است حتی جزء دامنه تابع موردنظر ما نباشد، چون در حدگیری مقدار تابع وقتی که $$x$$ به سمت $$a$$ میل می‌کند، مهم است، نه مقدار آن دقیقا در نقطه $$x= a$$.

جمع‌بندی مطالبی که تا اینجا در مورد مفهوم حد در ریاضی عمومی ۱ بیان شد، به این صورت می‌شود که اگر $$x$$ به سمت $$a$$ میل کند، حد یا لیمیت تابع $$f(x)$$ زمانی برابر با $$L$$ می‌شود که حد راست و چپ این تابع با هم برابر باشند. یعنی زمانی $$\lim_{x \rightarrow a} f(x) = L$$ برقرار است که تساوی $$\lim_{x \rightarrow a^+} f(x) = \lim_{x \rightarrow a^-} f(x) = L$$ را داشته باشیم.

تعریف دقیق‌ حد

تعریفی که تا اینجا برای حد ارائه شد، بیشتر جنبه کاربردی داشت. اگر بخواهیم حد تابعی را طبق اصول ریاضی عمومی ۱ دقیق‌تر تعریف کنیم، بهتر است به این شیوه عمل کنیم. اگر برای هر $$\epsilon > 0$$، فاصله کوچک و مثبتی به نام $$\delta$$ داشته باشیم، به گونه‌ای که هرگاه $$0 < |x-a| < \delta$$، درستی عبارت $$|f(x)-L| < \epsilon$$ برقرار باشد، در این صورت می‌توانیم بگوییم:

$$\lim_{x \rightarrow a} f(x) = L$$

دقت این تعریف برمبنای تعریف دو پارامتر بی‌نهایت کوچک به نام $$\epsilon$$ و $$\delta$$ است. این تعریف با تعریف بخش قبل کاملا معادل است، $$|f(x)-L| < \epsilon$$ به این معنا است که تابع $$f$$ خیلی خیلی به $$L$$ نزدیک می‌شود زمانی که $$0 < |x-a| < \delta$$ برقرار باشد، یعنی $$x$$ به سمت $$a$$ میل کند. در این تعریف هم به حالتی که $$|x-a| = 0$$ است، اشاره‌ای نمی‌شود.  به مثالی در این زمینه توجه کنید:

حد یک طرفه

پس از اینکه با مفهوم حد آشنا شدیم، می‌خواهیم ببینیم وضعیت حد تابعی مانند $$f$$ با نموداری به شکل زیر در دو حالت فرضی چگونه است:

• اگر مقادیر $$x$$ را بزرگتر از $$1$$ در نظر بگیریم.
• اگر مقادیر $$x$$ را کوچکتر از $$1$$ در نظر بگیریم.

به سمت راست نمودار تابع توجه کنید. همزمان با کاهش $$x$$ و نزدیک شدن آن به $$1$$، مقدار تابع $$f(x)$$ به عدد $$2$$ نزدیک می‌شود. در حالی که در سمت چپ نمودار و همزمان با تغییرات $$x$$ و دور شدن آن از $$1$$، مقدار تابع $$f(x)$$ به عدد $$1$$ نزدیک می‌شود. این دو حالت همان حد راست و چپ تابع $$f$$ هستند که به‌ ترتیب به‌صورت زیر نشان داده می‌شوند:

$$\lim_{x \rightarrow 1^+} f(x) = 2$$

$$\lim_{x \rightarrow 1^-} f(x) = 1$$

مشاهده می‌کنید که حد راست و چپ این تابع با هم برابر نشد. بنابراین اگر برای نشان دادن حد تابعی عبارت کلی به شکل $$x \rightarrow a^+$$ داشتیم، یعنی حد یک طرفه (حد راست) از ما خواسته شده است، در حالی که $$x \rightarrow a^-$$ نشان دهنده حد چپ است. پس با در نظر گرفتن این نکته که در حدگیری $$\lim_{x \rightarrow a} f(x) = L$$، هیچ‌گاه $$x$$ با $$a$$ برابر نیست، حدود یک طرفه به شکل زیر تعریف می‌شوند:

• در حد راست، $$x$$ از $$a$$ بزرگتر است (همسایگی راست).
• در حد چپ $$x$$ از $$a$$ کوچکتر است (همسایگی چپ).

قضایا و قواعد حدگیری

در این بخش قضایای حد در ریاضی عمومی ۱ را معرفی می‌کنیم. تسلط به این قواعد به شما کمک می‌کند تا در حدگیری و حل مسائل مرتبط که در بخش محاسبه جبری حد خواهید دید، سریعتر عمل کنید. در ادامه موضوع هر کدام از این قضایا را به اختصار و بدون اثبات توضیح می‌دهیم.

حد یک عدد ثابت

حد یک عدد ثابت همواره با خود آن عدد برابر است. پس برای هر عدد حقیقی مانند $$k$$ داریم:

$$\lim_{x \rightarrow a} k = k$$

حد حاصل‌ضرب عدد ثابت در تابع

به‌عنوان اولین قضیه حد، باید بدانیم اگر عدد ثابتی مانند $$k$$ در تابعی مانند $$f$$ ضرب شود، با فرض اینکه $$\lim_{x \rightarrow a} f(x) = L$$ است، حد این حاصل‌ضرب به‌صورت زیر محاسبه می‌شود:

$$\lim_{x \rightarrow a} kf(x) =k \lim_{x \rightarrow a} f(x) = kL$$

حد حاصل‌جمع و تفریق دو تابع

دومین قضیه حد نشان می‌دهد اگر حد دو تابع به‌صورت $$\lim_{x \rightarrow a} f(x) = L$$ و $$\lim_{x \rightarrow a} g(x) = M$$ باشد، در این صورت حد حاصل‌جمع یا تفریق این دو تابع به شکل زیر محاسبه می‌شود:

$$\lim_{x \rightarrow a}(f(x)\pm g(x))=\lim_{x \rightarrow a}f(x)\pm\lim_{x \rightarrow a}g(x)=L\pm M$$

حد حاصل‌ضرب دو تابع

فرض کنید برای حد دو تابع داریم: $$\lim_{x \rightarrow a} f(x) = L$$ و $$\lim_{x \rightarrow a} g(x) = M$$. در این صورت حد حاصل‌ضرب این دو تابع در همسایگی مشابه برابر است حاصل‌ضرب حد هر کدام از این توابع، یعنی داریم:

$$\lim_{x \rightarrow a} f(x)g(x) = \lim_{x \rightarrow a} f(x). \lim_{x \rightarrow a} g(x) = LM$$

حد تقسیم دو تابع

مشابه قضیه حد حاصل‌ضرب دو تابع، با داشتن $$\lim_{x \rightarrow a} f(x) = L$$ و $$\lim_{x \rightarrow a} g(x) = M$$، حد تقسیم این دو تابع در همسایگی مشابه برابر است تقسیم حد هر کدام از این توابع:

$$\lim_{x \rightarrow a} \frac{f(x)}{g(x)} = \frac{\lim_{x \rightarrow a} f(x)}{\lim_{x \rightarrow a} g(x)}= \frac{L}{M}$$

برقراری این قضیه منوط به صفر نبودن $$M$$ است، یعنی باید $$M\neq0$$.

حد توابع توان‌دار

با در نظر گرفتن $$n$$ به‌عنوان یک عدد حقیقی، همواره رابطه زیر برای حد یک تابع به توان $$n$$ برقرار است:

$$\lim_{x \rightarrow a}[f(x) ]^n =[\lim_{x \rightarrow a}f(x) ]^n$$

حد ترکیب دو تابع

در بخش توابع، توضیح دادیم که چگونه می‌توانیم ترکیب دو تابع را محاسبه کنیم. اگر داشته باشیم $$\lim_{x \rightarrow a} g(x) = L$$ و $$\lim_{x \rightarrow L} f(x) = f(L)$$، در این صورت حد ترکیب دو تابع $$f$$ و$$g$$ به شکل $$fog$$، برابر است با:

$$\lim_{x \rightarrow a} f(g(x)) = f(L)$$

حد یک تابع رادیکالی

با در نظر گرفتن این نکته که $$n$$ یک عدد صحیح و مثبت است، حد تابع رادیکالی زیر با این فرض که اگر $$n$$ زوج باشد، $$a$$ یک عدد مثبت است، برابر می‌شود با:

$$\lim_{x \rightarrow a} \sqrt[n]{x} = \sqrt[n]{a}$$

محاسبه حد از روی نمودار

محاسبه حد در ریاضی عمومی ۱ بسته به اینکه چه نوع اطلاعاتی در اختیار دارید، به دو روش انجام می‌شود. اگر نمودار تابع داده شده باشد، به روشی که در این بخش توضیح می‌دهیم می‌توان حد را به‌دست آورد. برای مثال، فرض کنید نمودار تابع $$f(x)$$ به شکل زیر داده شده است و می‌خواهیم رفتار این تابع را در همسایگی نقاط $$x = -5$$ و $$x = -2$$ و $$x = -1$$ و $$x =0$$ و $$x = 4$$ بررسی کنیم.

• ابتدا همسایگی راست و چپ نقطه $$x = -5$$ را در نظر می‌گیریم:

چون مقدار تابع در این نقطه یعنی $$f(-5)$$ با یک دایره توخالی نشان داده شده، نتیجه می‌گیریم که تابع در این نقطه تعریف نشده است. نکته دیگری که می‌توانیم در همسایگی چپ این نقطه با توجه به نمودار خطی شکل تابع داده شده نتیجه‌گیری کنیم این است که هر چه $$x$$ به $$-5$$ نزدیک و نزدیک‌تر شود، مقدار $$f$$ به $$2$$ نزدیک‌تر می‌شود. عبارت دقیق‌ ریاضیاتی در قالب حد یک طرفه یا حد چپ به شکل زیر نوشته می‌شود:

$$\lim_{x \rightarrow {-5‌‌}^-} f(x) = 2$$

از طرفی با نزدیک‌تر شدن $$x$$ از سمت راست به $$-5$$، باید نمودار منحنی شکل را در نظر بگیریم. همسایگی راست نقطه $$x = -5$$ به ما حد راستی را به‌صورت زیر می‌دهد:

$$\lim_{x \rightarrow {-5‌‌}^+} f(x) = -3$$

دقت کنید چون حد راست و چپ در این نقطه با هم برابر نیستند، در نقطه $$x = -5$$ حد نداریم.

• سپس همسایگی راست و چپ نقطه $$x = -2$$ را در نظر می‌گیریم:

مقدار تابع در این نقطه یعنی $$f(-2)$$ با یک دایره توپر روی محور xها نشان داده شده است که نشان دهنده صفر بودن مقدار تابع در این نقطه است. در همسایگی چپ این نقطه مشاهده می‌کنیم هر چه $$x$$ به $$-2$$ نزدیک و نزدیک‌تر شود، مقدار $$f$$ به $$3.5$$ نزدیک‌تر می‌شود. پس حد چپ این تابع به شکل زیر است:

$$\lim_{x \rightarrow {-2}^-} f(x) = 3.5$$

از طرفی با نزدیک‌تر شدن $$x$$ از سمت راست به $$-2$$، همسایگی راست نقطه $$x = -2$$  را داریم که به ما حد راستی به‌صورت زیر می‌دهد:

$$\lim_{x \rightarrow {-2}^+} f(x) = 3.5$$

حد راست و چپ در این نقطه با هم برابر شد، پس در نقطه $$x = -2$$ حد تابع $$f$$ برابر است با $$3.5$$. دقت کنید در این نقطه با اینکه مقدار تابع برابر است با صفر، اما حد آن مخالف صفر شد. در حقیقت در این نقطه برای تابع $$f$$ ناپیوستگی داریم که در بخش‌های بعد راجع‌به آن صحبت خواهیم کرد.

• حالا می‌رویم سراغ همسایگی راست و چپ نقطه $$x = -1$$:

مقدار تابع $$f$$ در این نقطه برابر است با $$-2$$. با در نظر گرفتن همسایگی چپ و راست، حد چپ و راست این نقطه به‌ترتیب برابراند با:

$$\lim_{x \rightarrow {-1}^-} f(x) = 0$$

$$\lim_{x \rightarrow {-1}^+} f(x) = -2$$

نابرابری حد چپ و راست نشان می‌دهد در این نقطه تابع $$f$$ حد ندارد.

• در ادامه همسایگی راست و چپ نقطه $$x =0$$ را بررسی می‌کنیم:

با توجه به اینکه $$f(0) = -2$$، حد چپ و راست هم در این نقطه همین مقدار می‌شود:

$$\lim_{x \rightarrow {0}^-} f(x) = -2$$

$$\lim_{x \rightarrow {0}^+} f(x) = -2$$

پس در این نقطه حد تابع $$f$$ برابر است با $$-2$$.

• آخرین نقطه‌ای که باید بررسی کنیم، $$x =4$$ است:

ابتدا مقدار تابع را در این نقطه پیدا می‌کنیم که به‌صورت $$f(4) = 0$$ است. دانستن مقدار تابع برای محاسبه حد لازم نیست. هدف ما از پیدا کردن مقدار تابع در هر نقطه این است که به تفاوت حد چپ و راست و مقدار تابع در هر نقطه توجه کنید. حد راست تابع برای این نقطه برابر است با بی‌نهایت، در حالی که حد چپ مقدار متناهی دارد. پس در این نقطه حد نداریم:

$$\lim_{x \rightarrow {4}^-} f(x) = -2$$

$$\lim_{x \rightarrow {4}^+} f(x) = \infty$$

روش جبری محاسبه حد

پس از اینکه آموختیم چگونه حد یک تابع را از روی نمودار آن تعیین کنیم، در این بخش روش محاسبه جبری حد را توضیح می‌دهیم. برای محاسبه حد اولین قدم این است که به قضایای حد کاملا مسلط باشید که در بخش‌های قبل آ‌ن‌ها را کامل توضیح دادیم. قضایای حد در کنار هم کمک می‌کنند که به عبارت ساده‌ای مانند $$\lim_{x \rightarrow a} x = a$$ برسیم و پاسخ نهایی را به‌آسانی به‌دست آوریم.

حد در بی‌ نهایت

یکی از مهم‌ترین مباحثی که در حدگیری مطرح می‌شود این است که اگر متغیر $$x$$ برای تابعی مانند $$f(x)$$ به سمت بی‌نهایت میل کند یا بدون مرز بزرگ شود، حدگیری چگونه انجام خواهد شد. در این شرایط می‌گوییم باید حد در بی‌نهایت را حساب کنیم که به‌ شکل $$\lim_{x \rightarrow \infty} f(x)$$ نشان داده می‌شود. با وجود اینکه در این نوع حدگیری $$x$$ به سمت بی‌نهایت میل می‌کند، اما ممکن است مقدار حدی تابع در این بازه عددی متناهی مانند $$L$$ شود:

$$\lim_{x \rightarrow \infty} f(x) = L$$

حد بی‌ نهایت

باید به تفاوت حد بی‌نهایت و حد در بی‌نهایت در ریاضی عمومی ۱ کاملا دقت کنید. در بخش قبل برای محاسبه حد در بی‌نهایت، مقدار متغیر $$x$$ به سمت بی‌نهایت میل می‌کرد در حالی که در این بخش، مقدار حد تابع $$f(x)$$ برابر با بی‌نهایت است. در این نوع حدود، حد تابع $$f(x)$$ در نقطه‌ای مانند $$x = a$$ وجود ندارد، یعنی مقدار تابع با نزدیک شدن $$x$$ به $$a$$ از چپ یا راست، بی‌نهایت زیاد یا کم می‌شود.  البته ممکن است حاصل حدی در بی‌نهایت هم بی‌نهایت شود.

مقایسه نرخ رشد

یکی دیگر از مباحث مطرح شده در مورد حد بی‌نهایت مقایسه نرخ رشد توابعی است که حد آن‌ها بی‌نهایت می‌شود. برای مثال فرض کنید می‌خواهیم ببینیم اگر $$m$$ و $$n$$ هر دو عدد صحیح و مثبت باشند و بدانیم که $$m$$ از $$n$$ بزرگتر است، در این صورت همزمان با $$x \rightarrow +\infty$$، چندجمله‌ای $$P_m(x)$$ سریعتر رشد می‌کند یا $$P_n(x)$$. برای این کار کافی است نسبت این دو چندجمله‌ای را بنویسیم و حد آن را در بی‌نهایت پیدا کنیم:

$$\lim_{x \rightarrow +\infty} \frac{P_m(x)}{P_n(x)} = \lim_{x \rightarrow +\infty} \frac{x^m+a_{m-1}x^{m-1}+ ...}{x^n+b_{n-1}x^{n-1}+ ...}$$

اگر صورت و مخرج رابطه بالا را بر $$x^n$$ تقسیم کنیم، خواهیم داشت:

$$= \lim_{x \rightarrow +\infty} \frac{x^{m-n}+a_{m-1}x^{m-n-1}+ ...}{1+\frac{b_{n-1}}{x}+ ...}$$

$$= \lim_{x \rightarrow +\infty} x^{m-n} (\frac{1+\frac{a_{m-1}}{x}+ ...}{1+\frac{b_{n-1}}{x}+ ...}) =+\infty$$

در واقع در آخرین رابطه حد عبارت داخل پرانتز برابر است با واحد، اما حد عبارت توانی بی‌نهایت می‌شود. پس در مقایسه نرخ رشد دو تابع چند جمله‌ای، مهم این است که بیشترین توان یا درجه برای کدام چند جمله‌ای از دیگری بزرگتر است. در این مثال فرض کرده بودیم $$m$$ از $$n$$ بزرگتر است. پس $$P_m(x)$$ سریعتر از $$P_n(x)$$ با $$x \rightarrow +\infty$$ به سمت بی‌نهایت میل می‌کند.

در ادامه چند رابطه مهم را در تکمیل مباحث بیان شده اضافه می‌کنیم:

• اگر $$m$$ یک عدد صحیح و مثبت بزرگتر از $$n$$ باشد، $$\lim_{x \rightarrow +\infty} \frac{x^m}{x^n} =\lim_{x \rightarrow +\infty} x^{m-n} =+\infty$$.
• اگر $$m$$ یک عدد صحیح و مثبت کوچکتر از $$n$$ باشد، $$\lim_{x \rightarrow +\infty} \frac{x^m}{x^n} =\lim_{x \rightarrow +\infty} x^{m-n} =0$$.
• اگر $$P(x)$$ یک چند جمله‌ای باشد، $$\lim_{x \rightarrow +\infty} \frac{P(x)}{e^x} = 0$$.
• $$\frac{1}{0^+}=+\infty$$ و $$\frac{1}{0^-}=-\infty$$
• $$\lim_{x \rightarrow +\infty} \frac{a^x}{x^n} =\lim_{x \rightarrow +\infty} \frac{e^x}{x^n} =+\infty$$
• $$\lim_{x \rightarrow +\infty} \frac{x^n}{a^x} =\lim_{x \rightarrow +\infty} \frac{x^n}{e^x} =0$$
• $$\lim_{x \rightarrow -\infty} \frac{e^x}{x^n} =0$$

رفع ابهام حد

یکی از نکات مهم در مورد حدهای بی‌نهایت این است که باید دقت کنیم آیا می‌شود آن‌ها را رفع ابهام کرد یا نه. در این بخش نشان می‌دهیم روش‌های رفع ابهام حد چگونه است. انواع ابهامات در حدگیری عبارت‌اند از:

• $$\frac{0}{0}$$
• $$\frac{\infty}{\infty}$$

اولین مرحله برای رفع ابهام حد این است که نوع ابهام را تشخیص دهیم. برای مثال، در رفع ابهام $$\frac{0}{0}$$ ممکن است دو تابع مانند $$f$$ و $$g$$ داشته باشیم که هر دو در نقطه‌ای مانند $$a$$ دارای حدی برابر با صفر هستند. بنابراین اگر این دو تابع را بر هم تقسیم کنیم، حاصل حد $$\frac{f}{g}$$ در همین نقطه برابر است با $$\frac{0}{0}$$. رفع ابهام این تابع، به معنای حذف عوامل صفر شونده از صورت و مخرج در این تابع کسری است.

در مورد رفع ابهام $$\frac{\infty}{\infty}$$ نیز می‌توان فرض کرد که دو تابع $$f$$ و $$g$$ در نقطه‌ای مانند $$a$$ دارای حد بی‌نهایت هستند. در این صورت حاصل حد $$\frac{f}{g}$$ در همین نقطه برابر است با $$\frac{\infty}{\infty}$$. به همین ترتیب حالت‌های مختلفی مانند $$1^ {\infty}, \infty ^0, 0\times \infty , \infty-\infty$$ ممکن است در مسائل حدگیری داشته باشیم که در تمامی این موارد بهتر است سعی کنیم ابتدا مسئله را به رفع ابهام‌های $$\frac{0}{0}$$ یا $$\frac{\infty}{\infty}$$ تبدیل کرده و سپس رفع ابهام را انجام دهیم.

در همین زمینه یکی از بهترین و آسان‌ترین ابزارهای رفع ابهام در حدگیری، استفاده از قاعده هوپیتال است. کاربرد این قاعده مستلزم آشنایی با مفهوم مشتق است، به همین دلیل توضیح این مبحث را در بخش مشتق خواهیم داشت. در ادامه با مثال نشان می‌دهیم چگونه می‌توان به کمک سایر روش‌های جبری مانند کاربرد اتحادها، رفع ابهام حدود را اجرا کرد.

انواع مجانب

بلافاصله پس از اینکه با مفهوم حد بی‌‌نهایت در ریاضی عمومی ۱ آشنا شدیم، می‌توانیم انواع مجانب را برای یک تابع تعیین کنیم. سه نوع مجانب برای توابع تعریف می‌شود که عبارت‌اند از:

• مجانب قائم
• مجانب افقی
• مجانب مایل

در ادامه هر کدام را به‌صورت مختصر توضیح می‌دهیم.

مجانب قائم

خط $$x = a$$ را مجانب قائم تابع $$f(x)$$ می‌نامیم، زمانی که حد این تابع در همسایگی نقطه $$x = a$$ بی‌نهایت شود. بنابراین یکی از راه‌های پیدا کردن مجانب قائم یک تابع این است که ببینیم در کدام نقطه حد آن بی‌نهایت می‌شود.

مجانب افقی

خط $$y = L$$ را می‌توانیم مجانب افقی تابعی مانند $$y = L$$ در نظر بگیریم، اگر داشته باشیم:

$$\lim_{x \rightarrow +\infty} f(x) = L$$

یا

$$\lim_{x \rightarrow -\infty} f(x) = L$$

به عبارت دیگر، برای پیدا کردن مجانب افقی یک تابع کافی است حد در بی‌نهایت را برای آن بررسی کنیم.

مجانب مایل

برخی از توابع ممکن است مجانبی داشته باشند که نه با تعریف مجانب افقی همخوانی دارد و نه با تعریف مجانب قائم. خط $$y‌= mx+b$$ مجانب مایل تابع $$f(x)$$ محسوب می‌شود، اگر یکی از دو تساوی زیر برقرار باشد:

$$\lim_{x \rightarrow +\infty} [f(x) - (mx+b)] = 0$$

$$\lim_{x \rightarrow -\infty} [f(x) - (mx+b)] = 0$$

قضیه فشردگی (قضیه ساندویچ)

در ادامه بررسی روش‌های محاسبه حد در ریاضی عمومی ۱، در این بخش قضیه مهمی به نام قضیه فشردگی یا Squeeze Theorem را توضیح می‌دهیم. فرض کنید می‌خواهیم $$\lim_{x \rightarrow 0} \frac{\ sinx}{x}$$ را حساب کنیم. اگر به روش محاسبه حد از روی نمودار عمل کنیم، با اینکه نقطه $$x = 0$$ جزء دامنه این تابع نیست (در این نقطه مقدار تابع با یک دایره توخالی نشان داده شده است)، اما می‌توانیم حد این تابع را وقتی که $$x$$ به $$0$$ نزدیک می‌شود، پیدا کنیم. طبق نمودار، این حد برابر است با $$1$$.

اگر بخواهیم به‌صورت جبری و فرمولی این حد را محاسبه کنیم، می‌توانیم از قضیه فشردگی استفاده کنیم. کافی است دو تابع به نام‌های $$g$$ و $$h$$ پیدا کنیم، به گونه‌ای که این تابع بزرگتر مساوی $$g$$ و کوچکتر مساوی $$h$$ باشد و همواره داشته باشیم $$\lim_{x \rightarrow 0} g(x) = \lim_{x \rightarrow 0} h(x)$$. برای مثال، $$‌ g (x) = \cos x$$ و $$‌ h (x) = \frac{1}{\cos x}$$ انتخاب‌های مناسبی برای تابع $$f (x) = \frac{\ sinx}{x}$$ هستند. با توجه به اینکه $$\lim_{x \rightarrow 0} \ cos x = \lim_{x \rightarrow 0} \frac{1}{\cos x}=1$$، می‌توانیم نتیجه‌گیری کنیم که $$\lim_{x \rightarrow 0} \frac{\ sinx}{x}$$ نیز برابر است با $$1$$.

پس قضیه فشردگی به این صورت تعریف می‌شود:

اگر تابعی مانند $$f$$ داشته باشیم، طوری که برای تمام $$x$$‌های نزدیک $$a$$ (و نه مساوی با $$a$$) داشته باشیم $$‌ g(x) \leq f(x) \leq h(x)$$، در این صورت اگر $$\lim_{x \rightarrow a} g(x) = \lim_{x \rightarrow a} h(x) = L$$، آن‌گاه $$\lim_{x \rightarrow a} f(x) = L$$. شکل زیر تعریف این قضیه را نشان می‌دهد. همان‌طور که مشاهده می‌کنید، تابع $$f$$ در حقیقت بین دو تابع $$g$$ و $$h$$ گیر افتاده است. همچنین در نزدیکی نقطه $$x = a$$ هر دو تابع $$g$$ و $$h$$ به یک مقدار نزدیک می‌شوند.

نکته: $$\lim_{x \rightarrow 0} \frac{\ sinnx}{nx} = 1$$

پیوستگی و تابع پیوسته

مفهوم پیوستگی توابع با توجه به نمودار آن‌ها کاملا واضح بنظر می‌رسد. برای مثال در شکل زیر تابع سمت راست دارای ناپیوستگی در نقطه $$x= 1$$ است،در حالی که تابع سمت چپ در این نقطه پیوسته است. اما تعریف دقیق‌تر پیوستگی در ریاضی عمومی ۱ به این صورت است: تابع $$f$$ در نقطه $$a$$ پیوسته است، اگر داشته باشیم $$\lim_{x \rightarrow a} f(x) = f(a)$$.

اگر می‌خواهید پیوستگی تابع$$f(x)$$ در نقطه‌ای مانند $$a$$ مشخص شود، بهتر است سه شرط زیر را بررسی کنید:

1. $$f(a)$$ وجود داشته باشد، به این معنا که $$a$$ متعلق به دامنه $$f(x)$$ است.
2. حد تابع $$f(x)$$ وجود داشته باشد، به این معنا که حد چپ و راست برای این تابع در این نقطه با هم مساوی هستند.
3. برابری نکته اول و دوم یا $$\lim_{x \rightarrow a} f(x) = f(a)$$.

تصویر زیر حالت‌های مختلفی که ممکن است در بررسی پیوستگی نقطه $$a$$ با آن‌ها مواجه شوید را نشان می‌دهد:

طبق این تصویر، می‌توانیم بگوییم ناپیوستگی انواع مختلفی دارد:

• ناپیوستگی رفع‌شدنی
• ناپیوستگی جهشی
• ناپیوستگی نامتناهی

ناپیوستگی رفع‌شدنی زمانی رخ می‌دهد که علی‌رغم برقراری شرط اول و دوم، شرط آخر برقرار نیست. ناپیوستگی جهشی از نابرابری حد چپ و راست ناشی می‌شود، یعنی حد چپ و راست وجود دارند، اما با هم برابر نیستند. تابع علامت یا Sign نمونه معروف یک تابع ناپیوسته با ناپیوستگی جهشی است. همچنین اگر یکی از حدود چپ و راست بی‌نهایت شوند، در این صورت ناپیوستگی نامتناهی داریم.

در ادامه تعاریف مهم پیوستگی، بد نیست به این نکته اشاره کنیم که اگر $$\lim_{x \rightarrow a^-} f(x) = f(a)$$ برقرار باشد، می‌گوییم تابع $$f$$ از چپ در نقطه $$a$$ پیوسته است، در حالی که اگر $$\lim_{x \rightarrow a^+} f(x) = f(a)$$ برقرار باشد، می‌گوییم تابع $$f$$ از راست در این نقطه پیوسته است. در حقیقت $$f$$ زمانی در نقطه $$a$$ پیوسته است که هم از راست و هم از چپ در این نقطه پیوسته باشد.

همچنین تابع $$f$$ در یک بازه بسته مانند $$[a,b]$$ زمانی پیوسته است که:

1. در تمام نقاط بازه باز $$(a, b)$$ پیوسته باشد.
2. در نقطه $$a$$ از چپ پیوسته باشد، یعنی $$\lim_{x \rightarrow a^-} f(x) = f(a)$$.
3. در نقطه $$b$$ از راست پیوسته باشد، یعنی $$\lim_{x \rightarrow b^+} f(x) = f(b)$$.

برای مثال، تابعی به شکل $$f(x) = \sqrt{4-x}$$، روی بازه‌‌ای به شکل $$(-\infty, 4]$$ پیوسته است. اغلب توابع چند جمله‌ای، توابع مثلثاتی، نمایی و لگاریتمی توابعی پیوسته هستند. به‌علاوه اگر دو تابع $$f$$ و $$g$$ در نقطه $$a$$ پیوسته باشند، حاصل‌جمع، تفریق، ضرب و تقسیم (به‌شرط $$g(a) \neq 0$$) آن‌ها نیز توابعی پیوسته خواهند بود. در همین راستا، پیوستگی دو تابع $$f$$ و $$g$$ در نقطه $$a$$ باعث می‌شود ترکیب این دو تابع نیز در همین نقطه پیوسته باشد.

قضیه حد مرکزی

یکی از معمول‌ترین سوالاتی که در ریاضیات مطرح می‌شود این است که آیا معادلاتی مانند $$e^x +x^2 = 0$$ یا $$e^x +x = 0$$ دارای جواب هستند یا خیر. در مورد معادله اول، با توجه به اینکه می‌دانیم $$e$$ همان عدد نپر و همواره مثبت است، پس $$e^x$$ نیز همواره مثبت است. $$x^2$$ نیز همیشه مثبت است. پس کل عبارت $$e^x +x^2$$ همواره برابر با یک عدد مثبت و بزرگتر از صفر است و هیچ‌گاه صفر نمی‌شود. به این ترتیب اولین معادله پاسخی ندارد. در مورد دومین معادله پاسخ دادن کمی مشکل است. اگر سعی کنیم با عدددهی نمودار تابع $$f(x) = e^x +x$$ را رسم کنیم، شکلی به‌صورت زیر به‌دست خواهیم آورد:

با توجه به اینکه هر دوی $$e^x$$ و $$x$$ توابعی پیوسته هستند، پس مجموع این دو تابع نیز یک تابع پیوسته است. بنابراین با وام گرفتن از مفهوم پیوستگی، می‌توانیم نتیجه بگیریم که این تابع قطعا در یک نقطه‌ محور افقی یا محور x را قطع می‌کند. پس این معادله دارای جواب است و قضیه حد مرکزی یا به اختصار IVT به ما کمک می‌کند تا این نقطه را پیدا کنیم. طبق این قضیه، با در نظر گرفتن بازه‌ی کوچکتری مانند $$(-0.4, -0.6)$$ و با توجه به اینکه $$f(-0.4)$$ منفی و $$f(-0.6)$$ مثبت است، می‌توانیم نتیجه بگیریم که حتما نقطه‌ای مانند $$x$$ در این بازه وجود دارد که برای آن $$f(x)=0$$ برقرار است. به‌طور دقیق‌تر این نقطه برابر است با $$x = -0.567$$.

بنابراین اگر تابعی مانند $$f$$ روی بازه بسته‌ای به صورت $$[a,b]$$ پیوسته باشد و $$N$$ مقداری بین $$f(a)$$ و $$f(b)$$ باشد ($$f(a) \neq f(b)$$)، طبق قضیه حد مرکزی همواره عددی مانند $$c$$ وجود دارد به گونه‌ای که $$f(c)= N$$. این قضیه تضمین می‌کند که اگر تابع $$f(x)$$ پیوسته بوده و $$N$$ مقداری بین $$f(a)$$ و $$f(b)$$ باشد، همواره خطی مانند $$y = N$$ داریم که نمودار این تابع را در نقطه‌ای مانند $$x=c$$ قطع می‌کند.

مشتق

شاید مهم‌ترین مبحث در ریاضی عمومی ۱، مشتق و کاربردهای آن است، چرا که در بخش‌های قبل مقدمات یادگیری این مبحث بیان شد و در بخش‌های بعد نیز، مفاهیمی مانند انواع انتگرال را داریم که درک آن‌، مستلزم تسلط به مفهوم مشتق است. در این بخش به تشریح مفهوم مشتق و نحوه محاسبه آن برای توابع مختلف خواهیم پرداخت و در بخش بعد با کاربردهای آن آشنا خواهیم شد.

تعریف مشتق

می‌دانیم شیب یک خط برابر است با نسبت تغییرات مقادیر $$y$$ به $$x$$. اگر تغییرات هر مقدار را با حرف یونانی \triangle نشان دهیم، می‌توانیم تعریف شیب خط را به زبان ریاضیات به شکل زیر بیان کنیم:

$$m = \frac{\triangle y}{\triangle x}= \frac{y_2-y_1}{x_2-x_1}$$

بنابراین شیب یا $$m$$ نشان دهنده میزان حساسیت یا وابستگی تغییرات $$y$$ همزمان با تغییر $$x$$ است. در همین راستا، خط سکانت (Secant) را داریم. این خط نمودار تابع را در دو نقطه قطع می‌کند. پس شیب آن، نشان‌دهنده متوسط تغییرات تابع است. برای مثال، فرض کنید طبق شکل زیر خط سکانتی با رنگ سبز روی نمودار تابع $$y=f(x)$$ رسم شده و آن را در دو نقطه $$Q$$ و $$P$$ قطع کرده است. شیب این خط با توجه به تغییرات $$x$$ روی نمودار برابر است با:

$$m = \frac{\triangle y}{\triangle x}= \frac{f(x+\triangle x) - f(x)}{\triangle x}$$

در مقابل خط سکانت، خط مماس بر نمودار را داریم که فقط و فقط در یک نقطه نمودار را قطع می‌کند. بنابراین شیب این خط را نمی‌توانیم با فرمول بالا محاسبه کنیم، چون در این فرمول باید حداقل مختصات دو نقطه از خط را داشته باشیم. اگر $$\triangle x$$ را کوچک و کوچک‌تر کنیم، در حدی که بتوان فرض کرد $$\triangle x \rightarrow 0$$، در این صورت شیب خط سکانت به شیب خط مماس نزدیک و نزدیک‌تر می‌شود. پس با بهره‌گیری از مفهوم حد، شیب خط مماس بر نمودار که بیانگر تغییرات لحظه‌ای تابع در نقطه‌ای مانند $$P$$ با مختصات $$(x,f(x))$$ است، به‌صورت زیر محاسبه می‌شود:

$$m = \lim_{\triangle x \rightarrow 0} \frac{f(x+\triangle x) - f(x)}{\triangle x}$$

به این ترتیب مشتق تابعی مانند $$f(x)$$ در نقطه $$x$$، طبق مراحل زیر محاسبه و تعریف می‌شود:

1. محاسبه شیب خط سکانت که در دو نقطه $$P=(x, f(x))$$ و $$Q=(x+ \triangle x, f(x+\triangle x))$$ منحنی تابع را قطع می‌کند.
2. محاسبه حد شیب بالا، با فرض اینکه $$\triangle x$$ به سمت صفر میل می‌کند.
3. اگر حد بالا وجود داشته باشد، مشتق تابع $$f(x)$$ در نقطه $$x$$ نیز وجود دارد و برابر با این حد است.

$$f'(x) = \lim_{\triangle x \rightarrow 0} \frac{f(x+\triangle x) - f(x)}{\triangle x}$$

$$f'(x)$$ با فرمول بالا، توصیف کننده مشتق تابع $$f(x)$$ نسبت به متغیر $$x$$ است. یک راه دیگر برای نمایش مشتق، استفاده از نماد $$\frac{d}{dx}$$ به‌جای قرار دادن علامت پریم روی تابع $$f(x)$$ است. نمادهای زیر همه یک مفهوم را منتقل می‌کنند:

$$y' = f'(x) =\frac{dy}{dx}=\frac{df}{dx}=\frac{d}{dx}f(x)$$

مفهوم مشتق‌پذیری

اگر برای تابعی مانند $$f(x)$$ در نقطه $$a$$ مشتقی به‌صورت $$f'(a)$$ وجود داشته باشد، در این صورت می‌گوییم $$f(x)$$ در این نقطه مشتق‌پذیر است. برای نمونه، به شکل‌های زیر توجه کنید. در نقاط $$x_1,x_2 ,x_3$$  ناپیوستگی داریم. پس در این نقاط حد وجود ندارد و مشتق‌ناپذیراند.

همچنین در نقطه $$x_4$$ برای شکل زیر، شیب خط مماس بر نمودار بی‌نهایت است که به معنای بی‌نهایت بودن مشتق یا در واقع مشتق‌ناپذیری است.

نکته: اگر تابع $$f(x)$$ در نقطه $$a$$ مشتق‌پذیر باشد، حتما در این نقطه پیوسته نیز هست. اما اگر تابع $$f(x)$$ در نقطه $$a$$ پیوسته باشد، نمی‌توانیم بگوییم حتما در این نقطه مشتق‌پذیر هم هست.

روش های جبری محاسبه مشتق

اگر بخواهیم مشتق تابع $$y = f(t )= t^2$$ را با استفاده از تعریف مشتق در ریاضی عمومی ۱ محاسبه کنیم، راه‌حل کوتاهی نخواهیم داشت:

$$y' = \lim_{\triangle t \rightarrow 0} \frac{f(t+\triangle t) - f(t)}{\triangle t}$$

$$y' = \lim_{\triangle t \rightarrow 0} \frac{(t+\triangle t)^2 - t^2}{\triangle t}=\lim_{\triangle t \rightarrow 0} \frac{t^2+2t\triangle t +\triangle t^2 - t^2}{\triangle t}$$

$$y' = \lim_{\triangle t \rightarrow 0} \frac{2t\triangle t +\triangle t^2 }{\triangle t}=\lim_{\triangle t \rightarrow 0} 2t +\triangle t =2t$$

حاصل مشتق‌گیری برابر شد با $$2t$$. یک راه‌حل سریعتر برای محاسبه مشتق توابع چندجمله‌ای مانند این تابع با فرم کلی $$f(x) =ax^n$$ استفاده از فرمول زیر است:

$$f'(x) =nax^{n-1}$$

به این ترتیب بسته به نوع تابع، می‌توانیم از فرمول مناسب برای مشتق‌گیری استفاده کنیم. برای مثال، در مورد توابع مثلثاتی با توجه به اینکه در بخش حدگیری توضیح دادیم همواره $$\lim_{x \rightarrow 0} \frac{\ sin x}{x} = 1$$ و $$\lim_{x \rightarrow 0} \frac{\ cos x - 1}{x} = 0$$ برقرار است، می‌توانیم به فرمول‌ مناسب برای محاسبه مشتق این توابع دست پیدا کنیم. همچنین اگر معکوس تابعی مانند $$‌ ‌f(x)$$ را با $$‌ ‌f^{-1}(x)$$ نشان دهیم، در این صورت مشتق معکوس این تابع در نقطه $$‌ ‌a$$ برابر است با:

$$‌ ‌[f^{-1}]'(a)=\frac{1}{f' [f^{-1}(a)]}$$

در جدول بالا خلاصه‌ای از مهم‌ترین فرمول‌های مشتق‌گیری برای توابع معروف آورده شده است. جهت آشنایی با فرمول‌ مشتق توابع پیچیده‌تری مانند توابع هایپربولیک، می‌توانید به مطلب «مشتق توابع هذلولوی و معکوس آن‌ها – از صفر تا صد» از مجله فرادرس مراجعه کنید.

قوانین مشتق‌گیری

به‌علاوه قوانین مشتق‌گیری را داریم که در محاسبه مشتق توابع پیچیده به ما کمک می‌کنند. برای مثال، اگر تابع $$f$$ یک تابع مشتق‌پذیر و $$c$$ یک عدد ثابت باشد، در این صورت داریم:

$$\frac{d}{dx}[cf(x)]=c \frac{d}{dx}f(x)$$

همچنین اگر هر دو تابع $$f$$ و $$g$$ مشتق‌پذیر باشند، روابط زیر برای جمع، تفریق، ضرب و تقسیم این توابع برقرار است:

$$\frac{d}{dx}[f(x)\pm g(x)]= \frac{d}{dx}f(x) \pm\frac{d}{dx} g(x)$$

$$\frac{d}{dx}[f(x). g(x)]= f(x) \frac{d}{dx}g(x) +g(x)\frac{d}{dx} f(x)$$

$$\frac{d}{dx}[\frac{f(x)}{g(x)} ]= \frac{g(x)\frac{d}{dx} f(x) - f(x) \frac{d}{dx}g(x)}{g(x)^2}$$

در مورد مشتق حاصل‌ضرب دو تابع، به رابطه $$\frac{d}{dx}[f(x). g(x)]\neq \frac{d}{dx}f(x) \frac{d}{dx} g(x)$$ دقت کنید.

مشتق مرتبه دوم و مراتب بالاتر

اگر تابع $$f$$ یک تابع مشتق‌پذیر باشد و مشتق آن یعنی $$'f$$ نیز مشخصات یک تابع را داشته باشد، در این صورت می‌توانیم مشتق $$'f$$ را نیز محاسبه کنیم. مشتق جدید، مشتق مرتبه دوم تابع $$f$$ است که با $$"f$$ نشان داده می‌شود:

$$y ''= f''(x) =\frac{d^2y}{dx^2}=\frac{df'}{dx}=\frac{d}{dx}(\frac{dy}{dx})$$

به همین ترتیب می‌توانیم مشتق مراتب بالاتر را در صورت وجود برای تابع $$f$$ محاسبه کنیم. $$n$$امین مشتق تابع $$f$$ را با $$f^{(n)}$$ نشان می‌دهیم که به‌صورت زیر تعریف می‌شود:

$$y^{(n)}= f^{n}(x) =\frac{d^ny}{dx^n}$$

مشتق زنجیره‌ ای

اگر $$g$$ یک تابع مشتق‌پذیر در $$x$$ و $$‌f$$ نیز در $$g(x)$$ مشتق‌پذیر باشد، در این صورت ترکیب این دو تابع یعنی $$h=fog = f (g(x))$$ در $$x$$ مشتق‌پذیر است و  $$h'(x)$$ به‌ شکل زیر نمایش داده می‌شود:

$$h'(x) = f'(g(x)).g'(x)$$

آنچه توضیح دادیم، قاعده زنجیره‌ای در مشتق‌گیری نام دارد. با در نظر گرفتن اینکه $$f'(g(x)) = \frac{df}{dg}$$ و $$g'(x) = \frac{dg}{dx}$$، مشتق زنجیره‌ای به شکل زیر محاسبه می‌شود:

$$\frac{df}{dx} =\frac{df}{dg} \frac{dg}{dx}$$

نکته: $$f(g(x)) \neq g(f(x))$$ و $$\frac{d}{dx} (f(g(x))) \neq \frac{d}{dx} (g(f(x)))$$.

مشتق ضمنی

در این بخش با مفهومی به نام مشتق ضمنی در ریاضی عمومی ۱ آشنا می‌شویم. فرض کنید تابعی به‌صورت $$‌f (x,y) = k$$ دارید که در آن $$‌ k$$ یک عدد ثابت است. فرآیند مشتق‌گیری ضمنی برای این تابع طبق مراحل زیر انجام می‌شود:

1. عملگر مشتق‌گیری $$‌\frac{d}{dx}$$ را در هر دو سمت معادله $$‌f (x,y) = k$$ اعمال کنید.
2. با در نظر گرفتن این نکته که $$‌y$$ تابعی است از $$‌x$$، مشتق‌گیری را با استفاده از قاعده زنجیره‌ای انجام دهید.
3. معادله را برای $$‌\frac{dy}{dx}$$ حل کنید.

کاربردهای مشتق

پس از اینکه با تعریف مشتق در ریاضی عمومی ۱ کاملا آشنا شدیم، در این بخش قواعد و قضایایی مانند قاعده هوپیتال، قضایای رول، کوشی و لاگرانژ را می‌آموزیم که در تمام آن‌ها از مشتق‌گیری با هدف خاصی استفاده شده است. همچنین، قضیه دیگری به نام قضیه تیلور یا Taylor's Theorem نیز در همین زمینه مطرح شده است که به دلیل طولانی شدن مطلب در این نوشته توضیح داده نشده است و می‌توانید جهت مطالعه این موضوع، به مطلب «قضیه تیلور – به زبان ساده» از مجله فرادرس مراجعه کنید. پیش از بیان این قضایا، ابتدا به بررسی ارتباط بین اکسترمم‌های یک تابع و مشتق آن خواهیم پرداخت.

نقطه بحرانی و اکسترمم‌ها

در بخش تابع و مفهوم آن با تعاریف اکسترمم‌های یک تابع که شامل نقاط ماکزیمم و مینیمم آن می‌شود، کاملا آشنا شدیم. در این بخش نشان می‌دهیم چگونه می‌توان با استفاده از مشتق، اکسترمم‌های هر تابع داده شده را تعیین کرد. ابتدا بهتر است نقطه بحرانی را تعریف کنیم. نقطه بحرانی نقطه‌ای مانند $$c$$ در دامنه تابع $$f$$ است که برای آن $$f'(c)$$ یا برابر است با صفر و یا تعریف نشده است.

بنابراین اگر تابع $$f$$ در نقطه $$x=c$$ اکسترمم نسبی داشته باشد، در این صورت نقطه $$c$$ حتما نقطه بحرانی تابع است. این نتیجه‌گیری، موضوع قضیه‌ای به نام قضیه فرما یا Fermat’s Theorem است. اما عکس این توضیح همیشه برقرار نیست. برای مثال، در تصویر بالا نقاطی را مشاهده می‌کنید که تعریف نقطه بحرانی برای آن‌ها صادق است، اما اکسترمم نسبی تابع محسوب نمی‌شوند.

قاعده هوپیتال

در بخش حدگیری اشاره کردیم که یکی از بهترین ابزارهای رفع ابهام در حد استفاده از قاعده هوپیتال است. در این قاعده به کمک مشتق‌گیری می‌توانیم نشان دهیم که حدود تعریف نشده دارای مقدار تعریف شده‌ای هستند و در نتیجه آن مقدار را به آسانی به‌دست می‌آوریم. فرض کنید می‌خواهیم حد تابعی به شکل زیر را پیدا کنیم:

$$\lim_{x \rightarrow a} \frac{f(x)}{g(x)}$$

در حالی که $$f$$ و $$g$$ به‌ شکل زیر تعریف شده‌اند:

$$\lim_{x \rightarrow a} f(x) = L_1$$

$$\lim_{x \rightarrow a} g(x) = L_2\neq 0$$

در این حالت خواهیم داشت:

$$\lim_{x \rightarrow a} \frac{f(x)}{g(x)} = \frac{L_1}{L_2}$$

اما اگر شرایط زیر را داشته باشیم، در این صورت با ابهام $$\frac{0}{0}$$ روبرو هستیم:

$$\lim_{x \rightarrow a} f(x) = \lim_{x \rightarrow a} g(x) = 0$$

در این شرایط $$\lim_{x \rightarrow a} \frac{f(x)}{g(x)}$$ تعریف نشده است و نمی‌توانیم رفتار دقیق این تابع را زمانی که $$x \rightarrow a$$ تعیین کنیم. در حدگیری‌هایی مانند $$\lim_{x \rightarrow 2} \frac{x^2 - 4 }{x-2}$$ یا $$\lim_{x \rightarrow 0} \frac{\sin x}{x}$$ دقیقا همین موقعیت را خواهیم داشت. اگر خاطرتان باشد، توضیح دادیم که برای مثال در مورد رفع ابهام $$\lim_{x \rightarrow 2} \frac{x^2 - 4 }{x-2}$$ می‌توانیم با باز کردن اتحادی که در صورت کسر داریم، عبارت کسری را ساده کرده و در نهایت به پاسخ تعریف شده برسیم.

در این بخش روش محاسبه این نوع حدگیری را با یک تکنیک راحت به نام قاعده هوپیتال توضیح می‌دهیم. ایده اصلی اثبات این قانون، کاربرد تقریب خطی است. قاعده هوپیتال در حالتی که ابهام یا تعریف‌نشدگی $$\frac{0}{0}$$ را داریم، به شکل زیر است:

اگر $$f$$ و $$g$$ دو تابع مشتق‌پذیر روی بازه بازی شامل نقطه $$a$$ باشند، در صورتی که $$\lim_{x \rightarrow a} f(x) = \lim_{x \rightarrow a} g(x) = 0$$، داریم:

$$\lim_{x \rightarrow a} \frac{f(x)}{g(x)} = \lim_{x \rightarrow a} \frac{f'(x)}{g'(x)}$$

به همین ترتیب قاعده هوپیتال در حالتی که ابهام یا تعریف‌نشدگی $$\frac{\infty}{\infty}$$ را داریم، به شکل مشابهی تعریف می‌شود. اگر $$f$$ و $$g$$ دو تابع مشتق‌پذیر روی بازه بازی شامل نقطه $$a$$ باشند، در صورتی که $$\lim_{x \rightarrow a} f(x) = \lim_{x \rightarrow a} g(x) =\pm \infty$$، داریم:

$$\lim_{x \rightarrow a} \frac{f(x)}{g(x)} = \lim_{x \rightarrow a} \frac{f'(x)}{g'(x)}$$

نکته: اگر تعریف‌نشدگی یا ابهام نداشته باشیم، استفاده از قاعده هوپیتال اشتباه است. همچنین در مورد سایر ابهامات لازم است طوری معادله تابع را تغییر دهیم که حتما به یکی از دو ابهام $$\frac{\infty}{\infty}$$ یا $$\frac{0}{0}$$ برسیم تا بتوانیم از قاعده هوپیتال استفاده کنیم.

قضیه مقدار میانگین یا قضیه لاگرانژ

در زمینه کاربردهای مشتق، چند قضیه مهم در ریاضی عمومی ۱ داریم که در این قسمت و بخش‌های بعد به معرفی و توضیح آن‌ها خواهیم پرداخت، مانند قضیه رول و قضیه مقدار مرکزی لاگرانژ یا به اختصار MVT که برای حل مسائل مختلف استفاده می‌شوند. قضیه رول در حقیقت یک زیرمجموعه از قضیه مقدار مرکزی یا قضیه لاگرانژ است. این دو قضیه مقدار میانگین توابع را محاسبه می‌کنند.

قضیه لاگرانژ برای پیدا کردن مقدار میانگین هر نوع تابعی در یک بازه تعریف شده بکار می‌رود. به‌عبارت دیگر، برای هر تابعی مانند $$f$$ که روی بازه بسته‌ای مثل $$[a,b]$$ تعریف شده، قضیه مقدار میانگین لاگرانژ قابل استفاده است اگر دو شرط زیر درست باشند:

• تابع $$f$$ روی بازه بسته‌ $$[a,b]$$ پیوسته باشد.
• تابع $$f$$ روی بازه باز $$(a,b)$$ مشتق‌پذیر باشد.

در این حالت حداقل یک نقطه مانند $$c$$ در بازه $$(a,b)$$ وجود دارد طوری که مشتق $$f$$ در آن نقطه برابر است با:

$$f'(c) =\frac{f(b)-f(a)}{b-a}$$

برای اینکه با مفهوم این قضیه بهتر آشنا شوید، حتما ابتدا بخش «قضیه حد مرکزی» در همین مطلب را مطالعه کنید. از نظر هندسی نیز اگر بخواهیم این قضیه را بررسی کنیم، می‌دانیم مشتق تابع در نقطه $$c$$ معادل است با شیب خط مماس بر نمودار در آن نقطه. این قضیه بیان می‌کند باید نقطه‌ای مانند $$c$$ بین $$a$$ و $$b$$ وجود داشته باشد، طوری که شیب خط مماس بر نمودار در این نقطه با شیب خط متصل کننده نقاط $$a$$ و $$b$$ برابر است:

قضیه رول

قضیه رول یا یا Rolle’s Theorem حالت خاصی از قضیه لاگرانژ است و بیان می‌کند که اگر تابع $$f$$ یک تابع پیوسته روی بازه بسته‌ای مانند $$[a,b]$$ بوده و روی بازه باز $$(a,b)$$ نیز مشتق‌پذیر باشد، در این صورت به شرط برقراری تساوی $$f(a) =f(b)$$ حداقل یک نقطه مانند $$c$$ در بازه $$(a,b)$$ وجود دارد طوری که مشتق $$f$$ در آن نقطه برابر است با صفر یا $$f'(c) =0$$.

کاربرد قضیه رول در پیدا کردن مقدار میانگین یک تابع در یک بازه تعریف شده است، به‌ویژه زمانی که مقدار تابع در ابتدای بازه با مقدار آن در انتهای بازه برابر باشد. طبق شکل بالا، صفر شدن مشتق تابع در نقطه‌ای مانند $$c$$ به این معنا است که خط مماس بر نمودار در این نقطه با محور xها موازی است.

نکته: عکس قضیه رول لزوما برقرار نیست، یعنی اگر در نقطه‌ $$c$$ عبارت $$f'(c) =0$$ برقرار بود، نمی‌توانیم بگوییم تمام پیش‌فرض‌های قضیه رول برقرار هستند.

قضیه مقدار میانگین کوشی

قضیه مقدار میانگین کوشی یا Cauchy’s Mean Value Theorem رابطه‌ای بین تغییرات دو تابع و مشتق‌ آن‌ها را در یک بازه مشخص و ثابت ارائه می‌دهد. این قضیه حالت خاصی از قضیه مقدار میانگین لاگرانژ محسوب می‌شود و به همین دلیل، آن را قضیه مقدار میانگین دوم هم می‌نامند. در قضیه کوشی فرض می‌کنیم اگر هر دو تابعی مانند $$f(x)$$ و $$g(x)$$ شرایط زیر را داشته باشند:

• روی بازه بسته‌ $$[a,b]$$ پیوسته باشند.
• روی بازه باز $$(a,b)$$ مشتق‌پذیر باشند.
• برای تمام $$x$$های متعلق به بازه $$(a,b)$$، همواره $$g'(x) \neq 0$$ برقرار باشد.

در این صورت نقطه‌ای مانند $$c$$ در بازه $$(a,b)$$ وجود دارد، به گونه‌ای که داریم:

$$\frac{f'(c)}{g'(c)}=\frac{f(b)-f(a)}{g(b)-g(a)}$$

دیفرانسیل

در آخرین مبحث از کاربردهای مشتق، مفهوم دیفرانسیل در ریاضی عمومی ۱ را توضیح می‌دهیم. اگر تابعی مانند $$y =f(x)$$ را در نظر داشته باشیم، در این صورت $$dy$$ و $$dx$$ دیفرانسیل نامیده می‌شوند و رابطه بین آن‌ها به‌صورت زیر است:

$$dy = f'(x) dx$$

دقت کنید اگر در تعریف تابع $$f$$ فقط $$f(x)$$ را بدون $$y$$ داشته باشیم، در این صورت دیفرانسیل‌های ما به‌صورت $$df$$ و $$dx$$ خواهند بود:

$$df = f'(x) dx$$

به این ترتیب می‌توانیم بگوییم مشتق تابع $$f$$ نسبت به $$x$$ برابر است با دیفرانسیل $$y$$ تقسیم بر دیفرانسیل $$x$$ ($$f'(x) = \frac{dy}{dx}$$). پس اگر تابع $$y =f(x)$$ یک تابع مشتق‌پذیر باشد، نتایج زیر را در مورد دیفرانسیل‌ها خواهیم داشت:

1. $$\triangle x$$ نشان‌دهنده یک تغییر خیلی خیلی کوچک و مخالف صفر در مقدار $$x$$ است.
2. $$dx$$ هم نشان‌دهنده یک تغییر خیلی خیلی کوچک و مخالف صفر در مقدار $$x$$ است.
3. $$\triangle y$$ نشان‌دهنده تغییرات $$y$$ همراه با تغییرات $$x$$ است.
4. رابطه $$\triangle y = f(x+\triangle x)-f(x)$$ برقرار است.
5. رابطه $$dy = f'(x) dx$$ نیز برقرار است.

کاربرد دیفرانسیل‌گیری در پیدا کردن مقدار تقریبی یک تابع یا تقریب زدن مقادیر خطا است.

مسیر کاربردی ریاضی عمومی ۱ با فرادرس

پیش از پرداختن به آخرین بخش از این مطلب از مجله فرادرس و در راستای کاربرد مباحثی که در ریاضی عمومی ۱ آموخته‌اید، مشاهده فیلم‌های آموزشی زیر از مجموعه فرادرس را به شما پیشنهاد می‌کنیم:

1. فیلم آموزش ریاضی مهندسی فرادرس
2. فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد فرادرس
3. فیلم آموزش ریاضیات و کاربرد آن در حسابداری، مدیریت و اقتصاد فرادرس
4. فیلم آموزش الگوریتم سینوس کسینوس SCA و پیاده سازی آن در متلب MATLAB فرادرس

انتگرال‌

در این بخش می‌آموزیم مفهوم انتگرال در ریاضی عمومی ۱ به چه معنا است. انتگرال روشی است برای جمع کردن تعداد زیادی جزء کوچک. به همین دلیل می‌توان از انتگرال در ساده‌ترین حالت برای محاسبه مساحت و حجم استفاده کرد. برای مثال، اگر بخواهیم مساحت زیر یک منحنی را به‌دست آوریم، می‌توانیم انتگرال تابعی که توصیف‌کننده این منحنی است را به‌دست آوریم. از طرفی انتگرال را «ضد مشتق یا پاد مشتق» هم می‌نامند، به این مفهوم که عملیاتی که عملگر انتگرال روی یک تابع انجام می‌دهد، کاملا عکس فرآیندی است که مشتق‌گیری روی یک تابع اجرا می‌کند.

انتگرال نامعین

اگر تابعی مانند $$‌F$$ را به‌عنوان پاد مشتق تابع $$‌f$$ در بازه $$‌I$$ در نظر بگیریم، در این صورت عبارت صحیح برای پاد مشتق $$‌f$$ روی این بازه $$‌‌F(x) + C$$ است که در آن $$‌‌ C$$ یک ثابت حقیقی است. به این ترتیب، مجموعه تمام پاد مشتق‌های تابع $$‌‌f(x)$$، انتگرال نامعین $$‌‌f(x)$$ نسبت به $$‌‌x$$ نام دارد که به شکل زیر نمایش داده می‌شود:

$$‌\int f(x)dx = F(x) + C$$

در عبارت بالا تابع $$‌‌f(x)$$ انتگرالده و $$‌‌dx$$ متغیر انتگرال‌گیری است. بنابراین حاصل انتگرال نامعین به فرم یک تابع است.

فرمول‌ها و قواعد انتگرال‌گیری

محاسبه انتگرال نامعین در ریاضی عمومی ۱ به کمک فرمول‌های مشخصی انجام می‌شود که با توجه به نوع تابع زیر انتگرال یا نوع انتگرالده متفاوت است. در ادامه بخشی از این فرمول‌های مهم برای شما قرار داده شده است:

$$‌\int kdx = kx + C$$

$$‌\int x^ndx = \frac{x^{n+1}}{n+1} + C, n \neq -1$$

$$‌\int \frac{1}{x}dx =\ln |x| + C, x \neq 0$$

$$‌\int a^{kx}dx =\frac{a^{kx}}{k \ ln a} + C, x \neq 0$$

$$‌\int \sin xdx =-\cos x + C$$

$$‌\int \cos xdx =\sin x + C$$

$$‌\int \sec^2 xdx =\tan x + C$$

$$‌\int \sec x \tan x dx =\sec x + C$$

$$‌\int \csc^2 xdx =-\cot x + C$$

$$‌\int \csc x \cot xdx =\csc x + C$$

$$‌\int \frac{dx}{1+x^2} =arctan x + C$$

$$‌\int \frac{dx}{\sqrt{1-x^2}} =arcsin x + C$$

همچنین یک سری قوانین برای محاسبه انتگرال حاصل‌ضرب یک عدد ثابت در تابع یا انتگرال مجموع و تفریق توابع داریم که لازم است در محاسبات رعایت شوند:

$$‌\int kf(x)dx = k\int f(x)dx$$

$$‌\int [f(x)\pm g(x) ] dx = \int f(x)dx \pm \int g(x)dx$$

نکته: در مورد انتگرال حاصل‌ضرب و تقسیم توابع روابط زیر را باید در نظر داشته باشید:

$$‌\int f(x). g(x)dx \neq \int f(x)dx \int g(x)dx$$

$$‌\int \frac{f(x)}{g(x)} dx \neq \frac{\int f(x)dx }{ \int g(x)dx}$$

انتگرال معین

تفاوت انتگرال معین با نامعین در حدود انتگرال‌گیری است. زمانی که در انتگرال‌گیری حدود انتگرال مشخص باشد، انتگرال معین داریم. بنابراین تابعی که به‌عنوان پاسخ در انتگرال نامعین به‌دست می‌آید، با عدددهی به یک عدد تبدیل می‌شود و پاسخ انتگرال معین یک عدد خواهد بود.

قضیه اساسی حسابان

با توجه به مفهوم انتگرال معین در ریاضی عمومی ۱ و با در نظر گرفتن این نکته که اگر $$f(x)$$ یک تابع پیوسته روی بازه بسته‌ $$[a,b]$$ باشد، می‌توانیم بنویسیم:

$$‌\int_{a}^{b} f(x)dx = F(x) |_{a}^{b} = F(b) - F(a)$$

که در آن $$F$$ پاد مشتق تابع $$f$$ است. این رابطه، قضیه اساسی حسابان نامیده می‌شود. دقت کنید لازم است دو پیش‌فرض اصلی یعنی پیوستگی تابع $$f$$ و بسته بودن بازه $$[a,b]$$ هر دو برقرار باشند تا بتوانیم از این قضیه استفاده کنیم. در این صورت، $$‌\int_{a}^{b} f(x)dx$$ نشان‌دهنده مساحت برآیند زیر نمودار تابع $$‌ f(x)$$ از $$‌a$$ تا $$‌b$$ است. به مثال زیر که در مورد لزوم بررسی این دو شرط اولیه است، توجه کنید.

انتگرال ناسره و آزمون همگرایی

مثال انتهای بخش قبل، ما را به گروهی از انتگرال‌ها به نام انتگرال‌های ناسره می‌رساند. این نوع انتگرال‌ها که در واقع نوعی انتگرال‌ معین محسوب می‌شوند، یک منطقه نامحدود را پوشش داده و شامل دو دسته‌اند:

• انتگرال‌هایی که در آن‌ها حداقل یکی از حدود انتگرال بی‌نهایت است.
• انتگرال‌‌هایی که دارای حدود متناهی یا تعریف شده‌اند، اما تابع زیر انتگرال در حداقل یک یا دو نقطه ناپیوسته است.

در مورد گروه اول، اگر تابع $$f(x)$$ یک تابع پیوسته روی بازه $$(a,\infty]$$ باشد، در این صورت انتگرال ناسره این تابع روی این بازه برابر است با:

$$‌\int_{a}^{\infty} f(x)dx =\lim_{R \rightarrow \infty} \int_{a}^{R} f(x)dx$$

به همین ترتیب، اگر تابع $$f(x)$$ روی بازه $$(-\infty,b]$$ پیوسته باشد، در این صورت انتگرال ناسره این تابع روی همین بازه برابر می‌شود با:

$$‌\int_{-\infty}^{b} f(x)dx =\lim_{R \rightarrow -\infty} \int_{R}^{b} f(x)dx$$

در روابط بالا اگر حد وجود داشته باشد و برابر با یک عدد متناهی شود، در این صورت می‌گوییم انتگرال ناسره ما همگرا شده است. در غیر این صورت، با $$‌\pm \infty$$ حاصل حدود بالا، انتگرال ناسره همگرایی ندارد. اما در مورد گروه دوم از انتگرال‌‌های ناسره، در نظر داریم که اگر تابع $$f(x)$$ در نقطه $$x=c$$ که جزء بازه $$[a,b]$$ است، ناپیوسته باشد، در این صورت خواهیم داشت:

$$‌\int_{a}^{b} f(x)dx= \int_{a}^{c} f(x)dx + \int_{c}^{b} f(x)dx$$

پس برای تعریف انتگرال ناسره از مفهوم حد در کنار قضیه اساسی حسابان استفاده کردیم. یکی از مهم‌ترین کاربردهای انتگرال‌های ناسره در مباحث آماری مانند توزیع احتمال است، چرا که تعیین برخی مقادیر مانند توزیع تجمعی یا مقدار انتظاری اغلب نیازمند محاسبه انتگرال‌هایی با حدود بی‌نهایت است.

روش تغییر متغیر در حل انتگرال

یکی از پرکاربردترین روش‌های حل انتگرال در ریاضی عمومی ۱ استفاده از روش جایگزینی یا تغییر متغیر است. این روش اغلب جهت حل انتگرال‌های نامعین استفاده می‌شود. اگر $$‌ u =g(x)$$ یک تابع انتگرال‌پذیر باشد که دامنه آن بازه‌ای مانند $$‌ I$$ است و $$‌ f$$نیز یک تابع پیوسته روی $$‌ I$$ باشد، در این صورت داریم:

$$‌\int f(g(x))g'(x)dx =\int f(u)du$$

معادلات دیفرانسیل و ثابت انتگرال‌گیری

معادله‌ای که شامل مشتق‌های یک تابع است و قصد داریم با حل آن به تابع اولیه برسیم، معادله دیفرانسیل نامیده می‌شود. برای مثال، $$‌f'(x) =2x$$ یک معادله دیفرانسیل با راه‌حل کلی $$‌f(x) =x^2+C$$ است. راه‌حل جزئی این معادله برای مشخص کردن مقادیر ممکن برای ثابت $$‌C$$ در شکل زیر نشان داده شده‌‌اند:

همان‌طور که ملاحظه می‌کنید، تعداد بی‌نهایت پاسخ وجود دارد که در این معادله دیفرانسیل صادق است. اما اگر فقط یک نقطه روی نمودار به نام «مقدار اولیه» داشته باشیم، می‌توانیم $$‌f(x)$$ را به‌طور کامل تعیین کنیم. چنین مسئله‌ای، مسئله مقدار اولیه در ریاضی عمومی ۱ نام دارد.