مشتق زنجیره ای — به زبان ساده
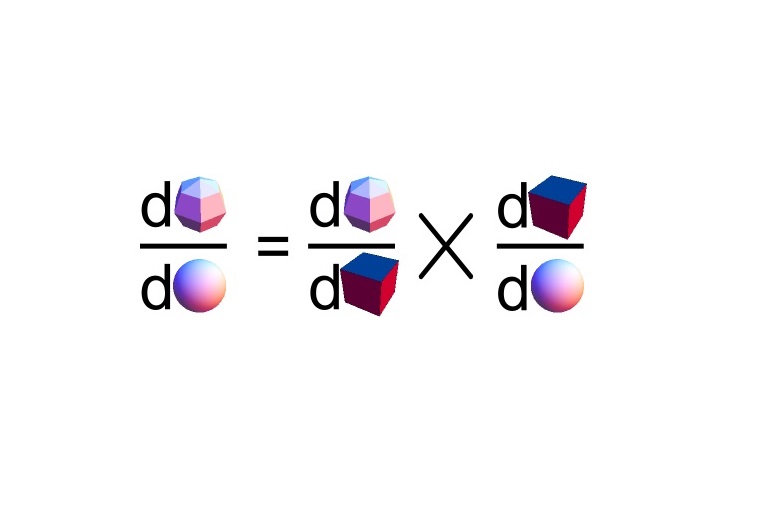
در آموزشهای قبلی مجله فرادرس، درباره مشتق و روشهای مشتقگیری بحث کردیم. در این آموزش، یک روش بسیار کارآمد و ساده را معرفی میکنیم که در فرایند مشتقگیری به ما کمک خواهند کرد.
احتمالاً مشتق توابعی مانند $$\sin (x)$$، $$x^8$$ و $$e^x$$ را بهخاطر دارید. اما درباره توابعی مانند $$\sin(2x-1)$$، $$(3x^2-4x+1)^8$$ یا $$e^{-x^2}$$ چه میتوانید بگویید؟ چگونه میتوانیم مشتق ترکیب توابع را بهدست آوریم؟ «قاعده زنجیرهای» (Chain Rule) ابزاری است که به ما این توانایی را میدهد از اطلاعات قبلی خود در زمینه مشتق توابع سادهتر $$f(x)$$ و $$g(x)$$، استفاده کرده و مشتق توابع ترکیبی $$f(g(x))$$ را محاسبه کنیم.
قضیه: اگر $$g(x)$$ یک تابع مشتقپذیر در x بوده و $$f(x)$$ در $$g(x)$$ مشتقپذیر باشد. با درنظر گرفتن $$y=f(g(x))$$ و $$u=g(x)$$، رابطه زیر برقرار است:
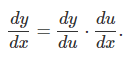
یا با یک نمادگذاری دیگر:

اثبات: فرض کنید $$g(x)$$ یک تابع مشتقپذیر در x بوده و $$f(x)$$ در $$g(x)$$ مشتقپذیر باشد. با درنظر گرفتن $$y=f(g(x))$$ و $$u=g(x)$$، از این واقعیت استفاده میکنیم که اگر $$y=f(x)$$ در x مشتقپذیر باشد، آنگاه
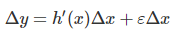
که در آن، وقتی $$\Delta x \rightarrow 0$$، $$\varepsilon \rightarrow 0$$. میتوان نوشت:

با جایگذاری $$\Delta u$$ از معادله اول در معادله دوم، داریم:
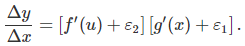
با در نظر گرفتن $$\Delta x \rightarrow 0$$، به عبارت زیر میرسیم و اثبات کامل میشود:
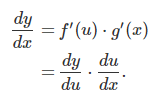
مثال 1
برای مشتقگیری از تابع $$\sin (2x-1)$$، عبارت $$u=2x-1$$ را در نظر میگیریم. بنابراین،
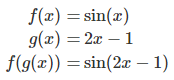
در نتیجه:

مثال 2
توابع f و g برای مشتقگیری از $$\left( 3x^{2} - 4x + 1 \right)^{8}$$ بهصورت زیر هستند:
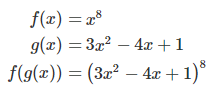
و مشتق بهراحتی محاسبه میشود:

مثال 3
مشتق تابع $$e^{-x^2}$$ با محاسبات زیر بهدست میآید:
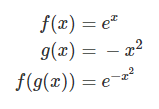
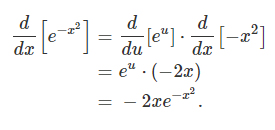
گاهی لازم است برای مشتقگیری یک تابع، چند بار از قاعده زنجیرهای استفاده کنیم. مثال زیر این مورد را بهخوبی نشان میدهد.
مثال 4
میخواهیم مشتق تابع $$\sqrt{\sin^{2} (3x) + x}$$ را محاسبه کنیم. در هر مرحله نشان داده شده که f چگونه انتخاب شده است.
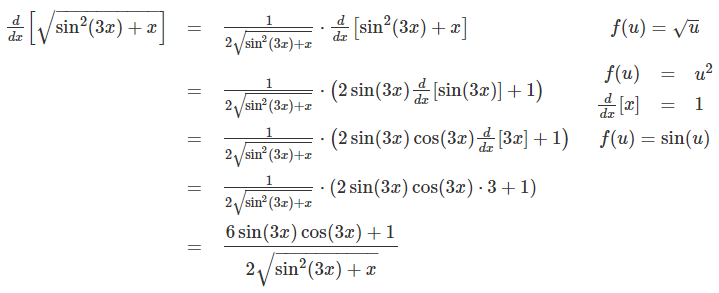
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- مجموعه آموزشهای ریاضیات و فیزیک پایه
- مجموعه آموزشهای دروس دبیرستان و پیشدانشگاهی
- مجموعه آموزشی جامع ریاضی دبیرستان – علوم تجربی
- مشتق جزئی — به زبان ساده
- مشتق ضمنی — به زبان ساده
^^











من ویدیو رو ندیدم ولی توضیحاتی رو که خوندم قشنگ فهمیدمش
ایولا دمتون گرم
کاش از یه صداپیشهٔ حرفهای استفاده میکردین 🙁
در نـهـایـتِ احترام، ایشون صداش و نحوهٔ گفتارش مناسب آموزش نیست 🙁