حد در ریاضی و محاسبه آن — به زبان ساده

ریاضیات همچون زنجیری است که تمامی حلقههای آن در هم تنیده است. برای مثال جهت درک مفهوم انتگرال بایستی بدانید که مشتق چیست. از طرفی بدون دانستن مفهوم حد (Limit) نمیتوان درکی از مشتق پیدا کرد. در وبلاگ فرادرس قصد داریم تا شما را با این حلقهها آشنا کنیم. بنیادیترین بخش به منظور درک حساب دیفرانسیل، مفهوم حد است. حساب دیفرانسیل از مفاهیم پرکاربرد ریاضیات است که حتی در علوم انسانی نیز مورد استفاده قرار میگیرد.

شاید بهترین مثال جهت توضیح حد را بتوان با استفاده از سرعت میانگین و یا سرعت نسبی بیان کرد. فرض کنید که میخواهید از نقطه A به نقطه B به نحوی حرکت کنید که مجبور باشید از نقطه C نیز بگذرید. در این حالت واضح است که با تقسیم کردن مسافت پیموده شده به زمان طی شدن این مسیر، سرعت متوسط بدست میآید.
فرض کنید در حالت واقعی پلیسی در نقطه C قرار گرفته و وظیفه او جریمه کردن است. در حقیقت برای او سرعت نسبی مهم نیست و فقط سرعت در نقطه C را برای نوشتن جریمه مد نظر قرار داده. این سرعت در واقع عددی است که شما در لحظه عبور از C ثبت میکنید، به همین دلیل به آن سرعت لحظهای در نقطه C گفته میشود.
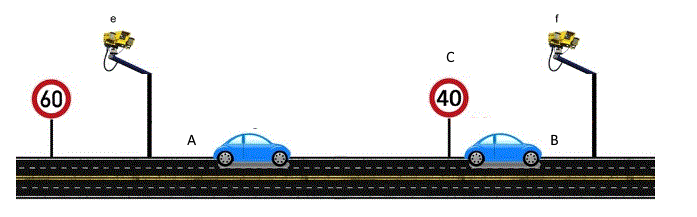
به نظر شما چطور میتوان سرعت دقیق را در لحظهای که در نقطه C قرار گرفتهایم، محاسبه کرد؟ لازم است بدانید که در حالت کلی پاسخ به این سوال آسان نیست. یکی از راهحلها این است که سرعت متوسط را در لحظهای بیابیم که بینهایت به نقطه C نزدیک هستیم. در این حالت دو نقطهای که سرعت متوسط را میان آنها محاسبه کردهایم، بسیار به هم نزدیک هستند (به شکل زیر توجه کنید). در حقیقت فاصله این دو نقطه نزدیک به صفر است. همچنین زمانی که طول میکشد تا متحرک بین این دو نقطه جابجا شود نیز بسیار اندک است. در حقیقت سرعت متوسط بین این دو نقطه از حاصل تقسیم دو عدد نزدیک به صفر بدست میآید. به نظر شما چگونه میتوان این حاصل تقسیم را محاسبه کرد؟ در ادامه به شما خواهیم گفت که چطور پلیس سرعت لحظهای شما را در نقطه C محاسبه کرده است.
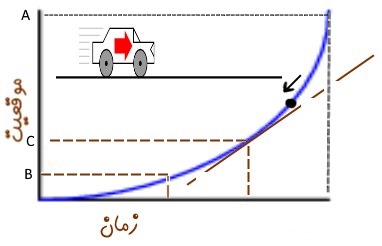
حال اجازه دهید تا مفهوم بالا را در قالب ریاضیات بیان کنیم. فرض کنید که تابع (s(t نشان دهنده مکان متحرک در هر لحظه است. همچنین فرض کنید که متحرک مفروض در زمان t0 در نقطه C قرار گرفته. در زمان t+Δt این متحرک در نقطهای بسیار نزدیک به C قرار میگیرد. بنابراین میتوان سرعت نسبی بین این دو نقطه را با استفاده از رابطه زیر محاسبه کرد.
![]()
اگر زمان Δt را به صفر نزدیک کنیم، مقدار دقیق سرعت در نقطه C بدست آمده است. این دقیقا مفهوم حد را نشان میدهد. بنابراین میتوان گفت سرعت لحظهای در نقطه C برابر است با:
![]()
برای نمونه تابع زیر را در نظر بگیرید.
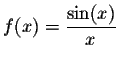
به نظر شما زمانی که x در نقطهای بسیار نزدیک به صفر انتخاب شود، مقدار این تابع به چه عددی میل میکند. شاید در ابتدا گیج شوید، چرا که حاصل مخرج این تابع برابر با صفر است. اجازه دهید که به صورت عددی مقدار x را به صفر نزدیک کنیم و به ازای آن تابع (f(x را بدست آوریم. در جدول زیر این کار انجام شده.
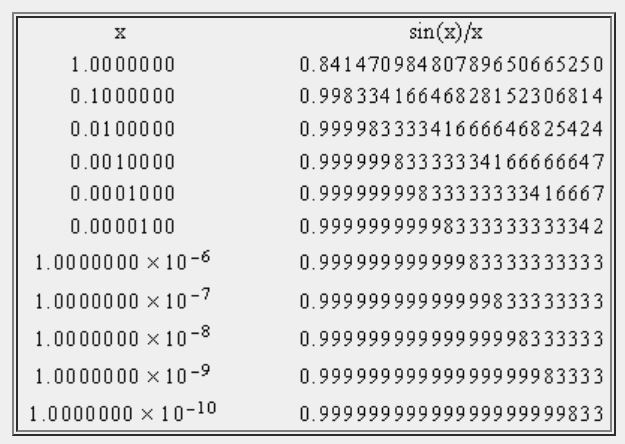
نتایج جدول جالب نیست؟ هرچه x به صفر نزدیک میشود، مقدار تابع به عدد ۱ میل میکند. بنابراین میتوان گذاره زیر را بیان کرد:
حد تابع هنگامی که x به صفر میل میکند، برابر با ۱ است.
در ریاضیات، بیان بالا را به صورت زیر نشان میدهند.
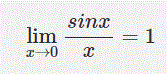
در شکل زیر تابع مفروض به ازای مقادیر نزدیک به ۱ رسم شده است. همانطور که در آن میبینید با نزدیک شدن متغیر x به صفر نمودار تابع به ۱ نزدیک میشود.
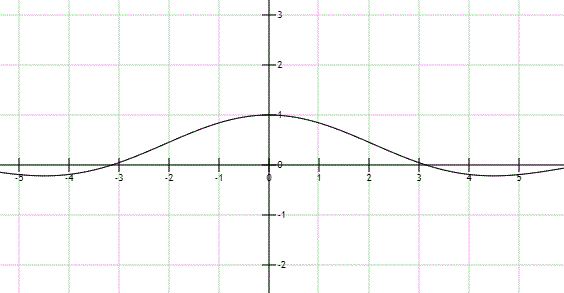
در هنگام محاسبه حد بایستی بسیار دقت کنید. در بعضی از موارد مقدار تابع به عددی خاص میل میکند اما ناگهان دچار پرش شده و مقدار آن عوض میشود. در ادامه مثالهایی را برای درک بهتر این موضوع بیان میکنیم.
بنابراین متوجه شدیم که با میل دادن x به صفر، مقدار تابع به ۱ نزدیک میشود. تعریف حد میگوید که شما هر اندازه که بخواهید بایستی بتوانید به ۱ نزدیک شوید. به بیانی ریاضیاتی میتوان گفت:
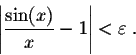
به نظر شما عبارت «xهای بسیار نزدیک به صفر» را در قالب ریاضیات چگونه بیان کنیم؟ این عبارت را میتوان به صورت زیر بیان کرد:
دلتایی (δ) بیشتر از صفر وجود دارد که با انتخاب آن عبارت صادق است.
تجربه نشان داده قبل از مطالعه ادامه مطلب، بهتر است به مدت ۵ دقیقه در مورد جمله بالا فکر کنید. دست به قلم شدن در هنگام اتصال به اینترنت، از شرایط لازم یادگیری حد است! بنابراین به ازا هر مقدار دلخواهی از ε بایستی بتوان δای پیدا کرد که همواره در نامساوی بالا صدق کند.
به نظر میرسد زمان آن رسیده تا تعریف جامعی از مفهوم حد ارائه دهیم. تابع (f(x را فرض کنید. تصور کنید که حد این تابع در نزدیکی نقطه c برابر با L است و یا به بیانی ریاضیاتی:
![]()
رابطه بالا به این معنا است که برای هر مقدار دلخواهی از ε بایستی δای وجود داشته باشد که در رابطه صدق کند و یا به عبارتی دیگر:
![]()
مقدار L، حد تابع (f(x در زمانی است که x به سمت c میل میکند. در بعضی موارد تابع (f(x دقیقا در نقطه c تعریف نشده، اما در مقادیر کمتر و یا بیشتر از آن تعریف شده است. از این رو میتوان از مقداری کمتر از c و یا بیشتر از c به تابع نزدیک شد. در این حالت است که مفهوم حد چپ و راست تعریف میشود. برای درک بهتر، تابعی را در نظر بگیرید که شکل آن به صورت زیر است.
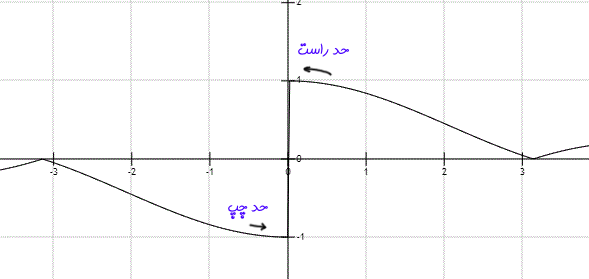
نمودار بالا تابع را نشان میدهد. اگر دقت کنید با توجه به نمودار اگر از سمت راست به نقطه x=0 نزدیک شویم تابع (f(x به ۱ میل میکند؛ اما اگر از سمت چپ به نقطه x=0 نزدیک شویم تابع به ۱- نزدیک میشود. از این رو برای یک تابع دو حد به صورت زیر تعریف میشود.
![]()
رابطه بالا حد راست تابع (f(x را در نقطه x=c نشان میدهد. از طرفی عبارت بیان شده در پایین حد چپ این تابع را در نقطه x=c بیان میکند.
![]()
زمانی که حاصل حد چپ و راست یک تابع در نقطهای خاص برابر باشند، میتوان گفت:
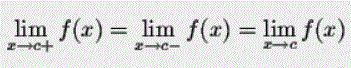
برای نمونه حاصل حد چپ و راست تابع را میتوان به شکل محاسبه کرد.
![]()
از آنجایی که حاصل حد چپ و راست این دو تابع با یکدیگر برابر نیست، پس بایستی گفت حد تابع (f(x در نقطه x=0 موجود نیست.
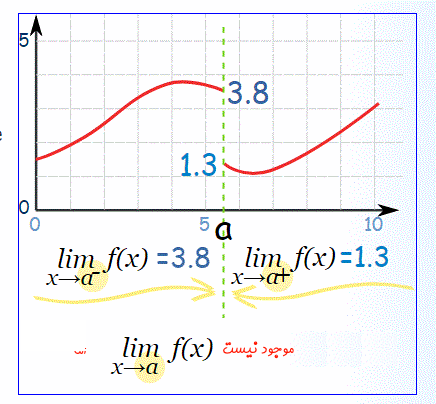
در شکل نشان داده شده که حد چپ و راست یک تابع در نقطه فرضی a موجود است اما با توجه به برابر نبودن آن دو، حد کلی تابع f وجود ندارد.
مثال ۱
حد تابع را در نقطه x=0 بیابید. پس از محاسبه مقادیر تابع در نزدیکی نقطه صفر، میتوان جدول زیر را ارائه کرد.

همانطور که میبینید با نزدیک شدن مقدار x به سمت صفر، تابع f در این نقطه به عدد مشخصی نزدیک نمیشود. از این رو این تابع در این نقطه حد ندارد. توجه کنید که برای مسائل حد نیاز نیست همواره ماشین حساب به همراه خود داشته باشید! چرا که در ادامه روشهایی را برای محاسبه حد توابع مختلف ارائه میکنیم.
مثال ۲
حد تابع x2 در نقطه x=2 چقدر است؟
به راحتی و با جایگذاری x در این رابطه میتوان حد آن را به صورت زیر محاسبه کرد.
![]()
فرض کنید میخواهیم این پاسخ را با استفاده از تعریف حد، اثبات کنیم.
در ابتدا بایستی به اندازه کافی به ۲ نزدیک شویم. بنابراین فرض میکنیم که متغیر x بین ۱ و ۳ قرار گرفته است. در نتیجه میتوان گفت:
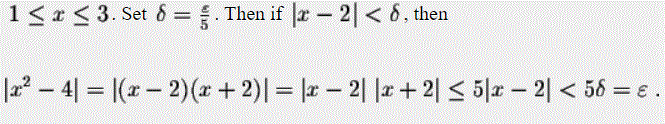
بنابراین اگر بخواهیم به اندازه ε به تابع f نزدیک شویم، بایستی به اندازه δ به متغیرش (x) نزدیک شویم.
مثال ۳
حد تابع را در نقطه x=۹ بیابید. با جایگذاری مقدار x در این تابع، بدیهی است که حد آن برابر با ۳ خواهد بود. اما اگر بخواهیم با استفاده از تعریف، جواب بدست آمده را اثبات کنیم. بایستی با فرض اینکه به اندازه δ به x نزدیک شویم، بایستی مقداری برای ε نیز یافت.
از این رو در ابتدا عبارت زیر را فرض میکنیم.
![]()
از طرفی میتوان نوشت:
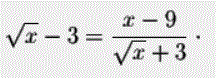
بنابراین بیان زیر درست است.
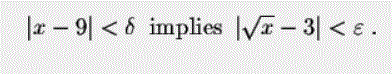
مثال ۴
حد زیر را بیابید.
با قرار دادن عدد در عبارت درون حد، به جواب زیر میرسیم:
در نتیجه:
مثال ۵
اگر به معنای باشد، کدامیک از گزینههای زیر درست است؟
سوال را میتوانیم با توجه به مفهوم قدر مطلق، به صورت زیر بازنویسی کنیم:
اگر
در نتیجه
چنین چیزی فقط در گزینه قابل مشاهده است.
بینهایت
یک عدد بزرگ را در ذهن خود تصور کنید؟ بینهایت عددی است که از آن بزرگتر است. به همین سادگی!

به نظر شما مقدار یک به روی بینهایت () معادل با چقدر است؟
پاسخ به این سوال در ابتد مشکل به نظر میرسد، چرا که بینهایت عدد مشخصی نیست که با معکوس کردن آن بتوان به مقدار خاصی رسید. تنها میتوان گفت که این عبارت شبیه به عبارات (زشت/۱) یا (بلند/۱) است. میتوان به طور تقریبی گفت که حاصل برابر با صفر است. اما این استدلال نیز دارای مشکل است. چرا که با تقسیم کردن ۱ به بینهایت نمیتوان به عدد دقیقی دست یافت. در حقیقت تعریف نشده است.
پاسخ حدی
اگرچه مقدار تعریف نشده است، اما میتوان پاسخی حدی برای آن یافت. در ادامه، شکل تابع و همچنین مقادیر آن برای چندین x که به صورت صعودی انتخاب شدهاند، نشان داده شده است.
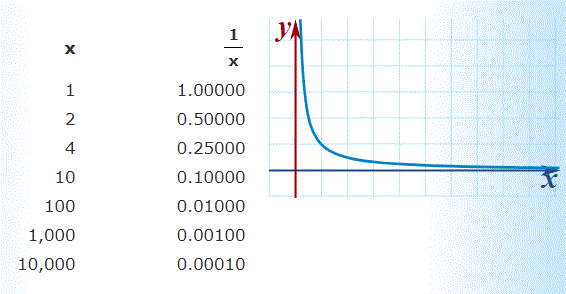
همانطور که میتوان دید با افزایش مقادیر x، مقدار تابع f به صفر نزدیک میشود. جالب است!
- نمیتوان مقدار را دقیقا تعیین کرد.
- مقدار تابع با افزایش x به صفر نزدیک میشود.
در حالت کلی حاصل تقسیم عدد ثابت a روی بینهایت برابر با صفر است. همچنین برای توابع چندجملهای همواره حاصل حد در بینهایت برابر با بینهایت است. برای نمونه حد تابع y=2x در بینهایت را میتوان به صورت زیر بیان کرد:
![]()
در خود تابع نیز اگر مقادیر x را جایگزین کنیم، میبینیم که تابع y به سمت بینهایت میل میکند. در ادامه میتوانید مقدار تابع را برای مقادیر صعودی x ببینید.
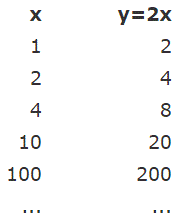
قانون بزرگترین توان
به منظور محاسبه حد در بینهایت میتوان بزرگترین توان موجود در تابع را در نظر گرفت. به مثالی که در ادامه آمده توجه کنید.
مثال ۶
حد تابع 2x2-5x را در بینهایت محاسبه کنید.
همانطور که در بالا بیان شد، برای محاسبه حد بینهایت یک چند جملهای، بزرگترین توان موجود در تابع در نظر گرفته میشود. بنابراین میتوان گفت:
![]()
شاید در مثال ۵ واضح بود که تابع به بینهایت میل میکند، اما در حالاتی که دو چند جملهایی به یکدیگر تقسیم شدهاند کار اندکی مشکلتر است. با استفاده از این قانون میتوان حد چنین توابعی را محاسبه کرد. منظور ما توابعی به شکل زیر است.
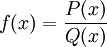
مثال ۷
حد تابع زیر را بیابید.
![]()
با استفاده از قانون بیشترین توان، میتوان جمله x3 را در صورت و 6x۳ را در مخرج نگه داشت. بنابراین حاصل حد برابر است با:
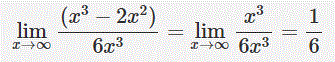
مثال ۸
حد تابع زیر را در بینهایت بیابید.
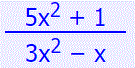
با نگه داشتن بیشترین توان موجود در صورت و مخرج خواهیم داشت:
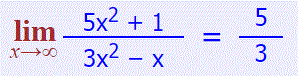













سلام مطالب مفید بودن خیلی ممنون
الان اگر یک مقدار به توان x بود و xبه بی نهایت میل میکرد چواب چی میشه
سلام ……………..
اثبات اینکه چه طوری قواعد ضزب و جمع و دیگر قواعد حد صادق ات اثبات این قوانین چیه ؟؟ اصن اثباتی داره یا به عنوان تعرف پذیرفتیمش
خیلی آموزنده است. از آقای بهنام محمدیان سپاسگزارم.
آقا کاربرد حد توی چیه
مثلاً مشتق در فیزیک خیلی خیلی استفاده میشود
حد چطوره کجاها استفاده میشود؟؟
ممنون
همین که مشتق در اصل از طریق حد بدست میاد فکر می کنم کافی باشه
سلام ممنون
سلام … در مثال شماره ۲ ، ۵ از کجا اومد؟
طرفین معادله منهای 2 شد