فرادرس
پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده
تابع در ریاضیات کاربردهای زیادی دارد. خصوصیات تابع از جمله «پیوستگی» (Continuity) نیز در شناخت توابع پر اهمیت است زیرا رفتار چنین توابعی، قابل پیش‌بینی بوده و در بیان بسیاری از پدیده‌های طبیعی می‌توان از آن‌ها استفاده کرد. در این نوشتار به معرفی «تابع پیوسته» (Continuous Function) پرداخته و به کمک مثال‌هایی با این دسته از توابع آشنا می‌شویم.
تابع پیوسته
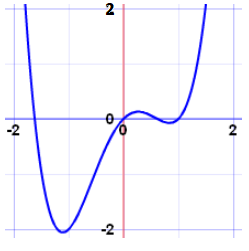
ابتدا برای تعریف تابع پیوسته، از منحنی تابع کمک می‌گیریم. اگر هنگام رسم منحنی تابع $$f(x)$$ هیچ انقطاعی وجود نداشته باشد و نمودار تابع بدون نقطه پرش باشد، تابع $$f(X)$$ را پیوسته می‌گویند. البته این توضیح می‌تواند یک تعریف غیر رسمی برای پیوستگی باشد ولی کمک می‌کند که ایده اصلی را درک کنیم. در تصویر زیر، منحنی یک تابع پیوسته دیده می‌شود.
نکته: این تابع می‌تواند یک چندجمله‌ای درجه ۴ باشد به شکل $$f(x)=ax^4+bx^3+cx^2+dx+e$$ باشد، زیرا به نظر می‌رسد در چهار نقطه محور افقی را قطع کرده است، یعنی چهار ریشه دارد. طبق یک قاعده کلی، چندجمله‌ای‌ها، پیوسته هستند.
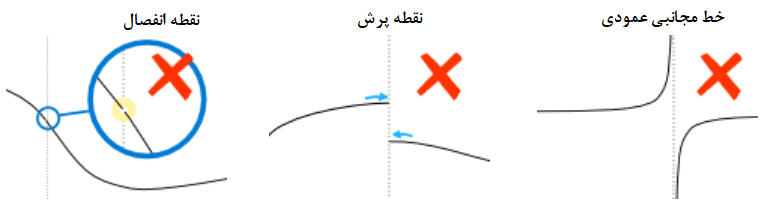
با استفاده از تعریف ارایه شده در بالا، شاید شناسایی «توابع گسسته» (Discontinues) راحت باشد. به این ترتیب تابع گسسته، تابعی خواهد بود که نمودار آن دارای انقطاع، بریدگی و یا پرش باشد. در نتیجه برای شناسایی چنین توابعی باید به دنبال نقاط انفصال بریدگی و یا پرش باشیم. نمودار توابع زیر پیوسته نیستند و دارای یک نقطه «انفصال» (Hole)، «پرش» (Jump) یا «خط مجانبی عمودی» (Vertical Asymptotic) هستند. در اینجا منظورمان از بریدگی همان خط مجانبی عمودی است.
برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
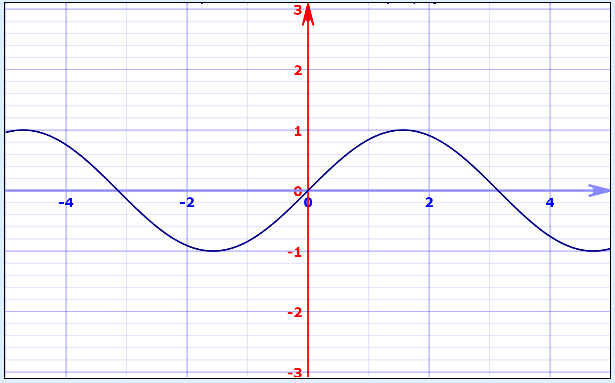
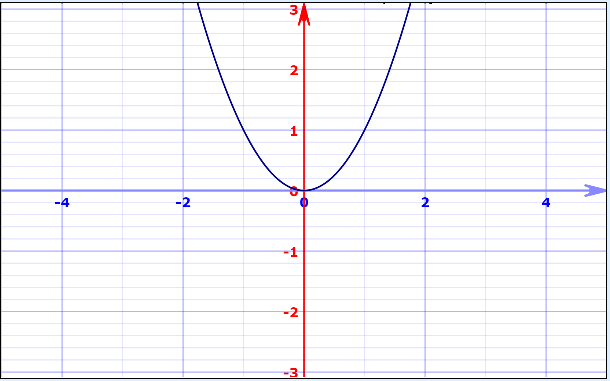
با توجه به این موضوع می‌توان پیوستگی و ناپیوستگی (گسستگی) توابع زیر را به کمک نمودار بررسی کرد. منحنی تابع $$sin(x)$$ و $$X^2$$ که در تصویرهای زیر به ترتیب دیده می‌شوند، نشان از پیوستگی تابع مورد نظر دارد. زیرا هیچ نقطه انفصال یا پرش یا خط مجانبی عمودی در آن‌ها دیده نمی‌شود.
در عوض تابعی مانند $$\frac{x^2-1}{x-1}$$ دارای نقطه انفصال است. نمودار این تابع در تصویر زیر دیده می‌شود. نقطه انفصال این تابع بوسیله دایره خاکستری نمایش داده شده است.
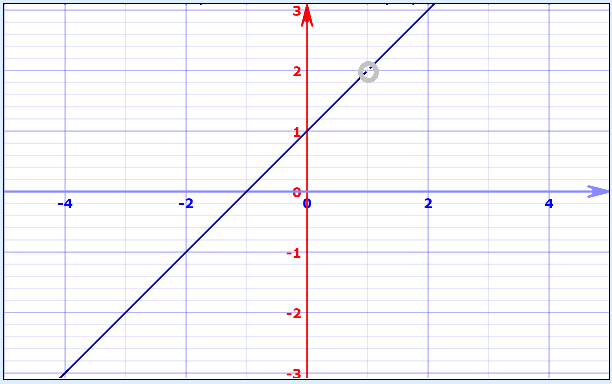
همینطور در تصویر زیر، نمودار مربوط به تابع $$\frac{1}{x-1}$$ رسم شده است که یک تابع گسسته محسوب می‌شود. روی نمودار نیز خط مجانبی عمودی با رنگ خاکستری دیده می‌شود. این خط، موازی محور عمودی است و از نقطه x=1 نیز می‌گذرد.
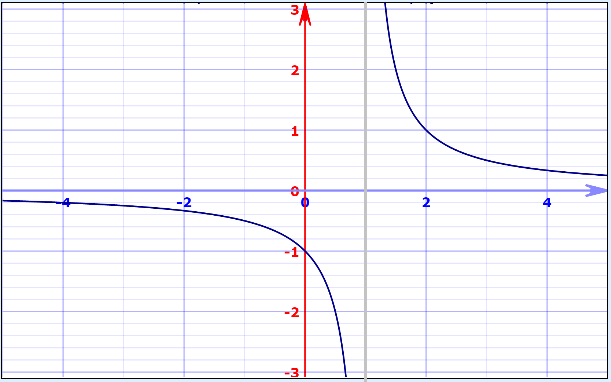
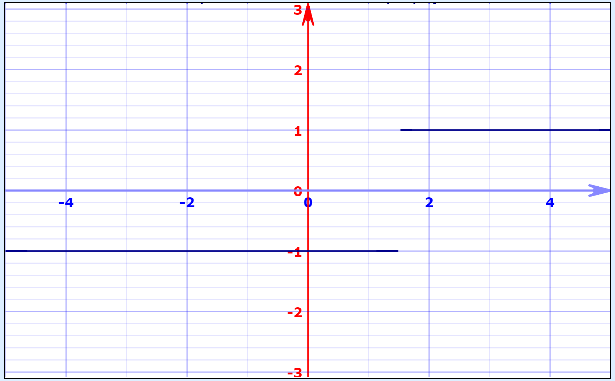
همچنین تابع $$sign(x-1.5)$$ نیز با پرشی با ارتفاع ۲ واحد در نقطه x=1.5، از گروه توابع گسسته است. تصویر زیر برای نمایش نمودار این تابع ترسیم شده.
نکته: منظور از تابع Sign آن است که اگر مقدار متغیر تابع (x) مثبت باشد، مقدار تابع برابر با ۱ و در غیراینصورت ۱- خواهد بود.
$$\large f(x)=sign(x)=\begin{cases}-1 & x < 0\\\;\;\;1 & x \geq 0\end{cases}$$
دامنه (Domain) و برد (Range) تابع
قبل از آنکه تعریف رسمی پیوستگی تابع را بررسی کنیم، باید با مفهوم دامنه و برد تابع آشنا شویم.
دامنه: مجموعه مقایری که به عنوان متغیر به تابع داده می‌شود و مقدار تابع به ازاء آن‌ها قابل محاسبه است، دامنه تابع نامیده می‌شود. دامنه تابع را با حرف D نشان می‌دهیم.
برد: مجموعه مقادیری که حاصل محاسبه تابع به ازاء اعضای مجموعه دامنه است، برد تابع گفته می‌شود. برد تابع را با حرف R نشان می‌دهیم.
بر این اساس می‌توان رابطه بین دامنه و برد تابع را توسط نمودار زیر نشان داد. پس یک تابع ممکن است برحسب دامنه آن پیوسته یا گسسته باشد.
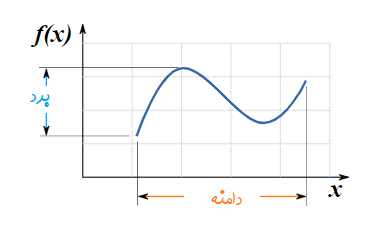
برای مثال اگر تابع $$\frac{1}{x-1}$$ را در نظر بگیرید، دامنه این تابع برابر است با:
$$\large D=\Re -\{1\}$$
که منظور اعداد حقیقی بدون مقدار ۱ است. زیرا مخرج این کسر به ازاء x=1 صفر شده و تابع قابل محاسبه نیست. پس می‌توان به این ترتیب گفت که این تابع در دامنه خود پیوسته است. بنابراین:
تابع که روی دامنه‌اش پیوسته باشد، تابع پیوسته نامیده می‌شود
تعریف اصلی پیوستگی براساس حد تابع
«حد» (Limit) یکی از مفاهیم اصلی و مهم در ریاضیات محسوب می‌شود که کاربردهای متعددی نیز دارد. برای مثال برای محاسبه انتگرال و یا مشتق از تعریف حد استفاده می‌شود تا فرمول‌های مربوط به نحوه محاسبه انتگرال و یا مشتق اثبات شوند. همچنین تعریف اصلی پیوستگی براساس مفهوم حد صورت می‌گیرد. بنابراین بهتر است ابتدا مطلب حد در ریاضی — به زبان ساده را مطالعه کرده باشید.
تعریف پیوستگی: تابع f را پیوسته گویند اگر برای هر مقدار از دامنه‌اش (مانند c)، داشته باشیم.
$$\large lim_{x \rightarrow c} f(x)=f(c), \;\;\;\; \forall c\in D$$
این رابطه بیان می‌کند زمانی که x به سمت c نزدیک می‌شود، تابع $$f(x)$$ نیز به $$f(c)$$ نزدیک و نزدیک‌تر می‌شود. البته باید توجه داشت که نزدیک شدن x به c هم از سمت مقدارهای کوچکتر از c و هم مقدارهای بزرگتر از c صورت می‌گیرد.
حد چپ: گر مقدار متغیر از سمت مقدارهای کوچکتر از c به آن نزدیک شود، حد چپ محاسبه شده است. در تصویر زیر حد چپ برای تابع نمایش داده شده است.
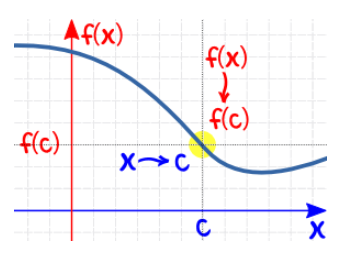
حد راست: همچنین اگر متغیر از سمت راست (یعنی مقادیر بزرگتر) به مقدار c نزدیک شود، حد راست محاسبه می‌شود. در تصویر زیر نیز حد راست برای تابع f دیده می‌شود.
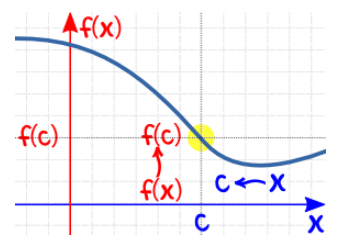
به این ترتیب می‌توان پیوستگی تابع را در نقطه c با توجه به سنجش سه شرط زیر بررسی کرد:
- تابع در نقطه c تعریف شده باشد یا c در دامنه تابع باشد.
- تابع در نقطه c دارای حد باشد. فرض کنید مقدار این حد برابر با L باشد.
- مقدار تابع در نقطه c با حد تابع در آن نقطه برابر باشند. یعنی $$f(c)=L$$
نکته: برای آنکه تابع f در نقطه c دارای حد باشد، باید حد راست و حد چپ تابع در نقطه c برابر باشند.
بنابراین برای آنکه بدانیم آیا تابع f در دامنه‌اش پیوسته است، باید برای همه نقاط دامنه سه شرط بالا را چک کنیم. که ممکن است کار سختی به حساب آید. ولی با استفاده از روش‌هایی مانند مشتق‌پذیری تابع می‌توان پیوستگی آن را بررسی کرد. البته در این مطلب هدف آشنایی با مفهوم پیوستگی است پس به چنین مواردی نخواهیم پرداخت. برای آشنایی بیشتر با توابع پیوسته به بررسی چند مثال می‌پردازیم.
مثال ۱
پیوستگی تابع $$\frac{x^2-1}{x-1}$$ را در روی اعداد حقیقی بررسی می‌کنیم. با توجه به نمودار شماره ۲، مشخص است که نقطه 1 متعلق به دامنه تابع نیست. ولی از آنجایی که بررسی پیوستگی روی همه اعداد حقیقی باید بررسی شود، می‌توان نتیجه گرفت که این تابع پیوسته نیست.
حال فرض کنید که ناحیه‌ای که قرار است پیوستگی تابع را در آن بررسی کنیم به مجموعه اعداد حقیقی کوچکتر از ۱ تغییر یافته باشد. از آنجایی که نمودار مربوطه در این ناحیه هیچ نقطه انفصالی ندارد، تابع $$\frac{x^2-1}{x-1}$$ روی مجموعه $$(-\infty, 1)$$ پیوسته است.
قواعد پیوستگی برای چندجمله‌ای‌ها
با توجه به مثال بالا می‌توان زمانی که تابع ما با استفاده از عملیات جبری روی چند جملهایها ساخته می‌شود، قواعد کلی زیرا برای پیوستگی آن‌ها در نظر گرفت:
- چند جمله‌ای ها روی دامنه‌شان یعنی اعداد حقیقی، پیوسته هستند.
- جمع و تفریق دو یا چند عبارت چندجمله‌ای نیز روی اشتراک دامنه‌هاشان (باز هم اعداد حقیقی) پیوسته است.
- ضرب چند جملهایها روی اشتراک دامنه‌هاشان پیوسته هستند.
- تقسیم دو چند جمله‌ای روی اشتراک دامنه‌هایشان (یعنی اعدادی حقیقی) پیوسته است به جز مقدارهایی که مخرج را صفر می‌کند. زیرا دامنه توابع حاصل از تقسیم دو چندجمله‌ای، همه اعداد حقیقی به جز ریشه‌های مخرج است.
- توابع حاصل از به توان رساندن چندجمله‌های با توان صحیح روی اعداد حقیقی پیوسته است.
- توابع حاصل از گرفتن ریشه زوج از یک چندجمله‌ای روی همه اعداد حقیقی به جز مقدارهایی که چند جمله‌ای را منفی می‌کنند پیوسته هستند.
در مثال بالا تقسیم دو چندجمله‌ای بررسی شد که در ریشه مخرج پیوسته نبود. این حکم با توجه به قواعدی که گفته شده به راحتی مشخص می‌شود.
مثال ۲
تابع دو ضابطه‌ای $$h(x)$$ را در نظر بگیرید. قرار است، یپوستگی این تابع را روی مجموعه اعداد حقیقی بررسی کنیم.
$$\large h(x)=\begin{cases}2 & x\leq 1\\x & x > 1\end{cases}$$
نمودار این تابع در زیر رسم شده است.
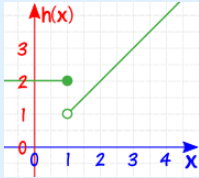
با توجه به تعریفی که برای پیوستگی توسط مفهوم حد بیان شد، نمی‌توان این تابع را پیوسته در نظر گرفت. زیرا حد راست آن در نقطه x=1 برابر با 1 و حد چپ در همان نقطه برابر با ۲ است. بنابراین این تابع در نقطه x=1 حد ندارد پس پیوسته نیست. در نتیجه نمی‌توان پیوستگی تابع را روی همه اعداد حقیقی در نظر گرفت.
مثال ۳
تابع قدر مطلق نیز یک تابع دو ضابطه‌ای است که به صورت زیر تعریف می‌شود:
$$\large |x|=\begin{cases}-x & x\leq0 \\x & x > 0 \end{cases}$$
در نقطه x=0 تابع به شدت تغییر می‌کند ولی هیج نقطه انفصال یا گسستگی در تابع دیده نمی‌شود. این تابع در نقطه x=0 پیوسته است، زیرا مقدار صفر در دامنه تابع بوده و حد تابع در این نقطه نیز با مقدار تابع برابر است.
$$\large \lim _{x \rightarrow 0}|x|=0 $$
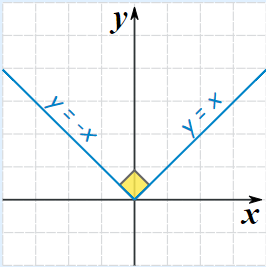
نکته: با توجه به مفهوم حد راست و چپ، نماد نمایش این دو گونه حد به صورت زیر است.
$$\large \lim _{x \rightarrow c^+}f(x) $$:حد راست
$$\large \lim _{x \rightarrow c^-}f(x) $$:حد چپ
معرفی فیلم آموزش ریاضی و آمار (۱) – پایه دهم علوم انسانی
یکی از آموزش‌های ویدیویی دوره دبیرستان فرادرس، «آموزش ریاضی و آمار (۱) – پایه دهم علوم انسانی» است که به طور ویژه مربوط به دانش‌آموزان رشته علوم انسانی است. این آموزش ویدیویی در قالب چهار درس و در زمان ۶ ساعت و ۱۹ دقیقه تدوین شده است. در درس یکم، معادله درجه دوم مورد بحث قرار گرفته که شامل مطالب اصلی درس، نکات مهم و مثال‌های حل شده است. در درس دوم، موضوع مهم تابع ارائه شده و در آن، به موارد مهمی از قبیل تعریف ضابطه و تابع، رسم آن، دامنه و برد تابع و… پرداخته شده است. کار با داده‌های آماری موضوع درس سوم است. در نهایت، در درس چهارم به طور کامل، مطالب کتاب درسی درباره نمایش داده‌ها ارائه شده است.
- برای مشاهده فیلم آموزش ریاضی و آمار (۱) – پایه دهم علوم انسانی + اینجا کلیک کنید.
معرفی فیلم آموزش ریاضی پایه دانشگاهی
یکی از آموزش‌هایی که برای آشنایی بیشتر با مبحث اتحاد و تجزیه می‌توانید به آن مراجعه کنید، آموزش ریاضی پایه دانشگاهی است. این آموزش که مدت آن ۱۲ ساعت و ۴۶ دقیقه است، در قالب ۱۰ درس تهیه شده است.
در درس اول، مجموعه‌ها، مجموعه اعداد، توان، ب.م.م و ک.م.م معرفی شده‌اند. موضوعات درس دوم، چندجمله‌ای‌ها و اتحاد و تجزیه است. در درس سوم، نامساوی‌ها، نامعادلات، طول پاره‌خط، ضریب زاویه و معادله خط مورد بحث قرار گرفته‌اند. مثلثات موضوع مهم درس چهارم است. تصاعد حسابی و هندسی در درس پنجم بررسی شده‌اند. تابع و دامنه و برد آن موضوعات مهم درس ششم هستند. در درس هفتم، تساوی دو تابع، اعمال جبری روی تابع و ترکیب توابع ارائه شده‌اند. در درس هشتم به توابع زوج و فرد، تابع یک به یک و تابع وارون پرداخته شده است. انواع توابع از قبیل تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق و تابع جزء صحیح موضوع درس نهم هستند. در نهایت، در درس دهم توابع نمایی و لگاریتمی مورد بحث قرار گرفته‌اند.
- برای مشاهده فیلم آموزش ریاضی پایه دانشگاهی + اینجا کلیک کنید.
معرفی فیلم آموزش ریاضی پایه (مرور و حل تست کنکور ارشد)
فیلم آموزش ریاضی پایه (مرور و حل تست کنکور ارشد) در ۵ ساعت و ۱۶ دقیقه و در قالب ۴ درس تهیه شده است. درس یکم این آموزش درباره مجموعه‌ها، چندجمله‌ای‌ها، اتحاد و تجزیه، نامساوی و نامعادلات است. در درس دوم، معادله درجه 2 مورد بررسی قرار گرفته است. موضوع درس سوم مثلثات است. در نهایت، در درس چهارم به تابع، دامنه و برد آن، تساوی دو تابع، اعمال جبری روی تابع، ترکیب توابع، توابع زوج و فرد، توابع یک به یک، وارون تابع، تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق، تابع جزء صحیح، تابع نمایی و تابع لگاریتمی پرداخته شده است.
- برای مشاهده فیلم آموزش ریاضی پایه (مرور و حل تست کنکور ارشد) + اینجا کلیک کنید.
اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
سلام. در یک متنی خواندم
(ریشه های چندجمله ای نسبت به ضرایب ان پیوسته هستند.)
لطفا توضیح می دهید منظور چی بوده؟