مختصات قطبی — از صفر تا صد

دستگاه مختصات، مفهومی است که با استفاده از آن مکان نقاط در یک صفحه تعیین می‌شوند. معمولا در فیزیک و ریاضیات دو یا سه محور عمود بر هم در نظر گرفته شده و فاصله نقطه‌ی مفروض از محور‌ها به‌عنوان مختصات نقطه در نظر گرفته می‌شود. به چنین دستگاه مختصاتی، دستگاه مختصات کارتزینی (Cartesian Coordinate System) گفته می‌شود. احتمالا تاکنون با این نوع از دستگاه مختصات آشنا شده‌اید. از این رو در این مطلب قصد داریم تا دستگاه مختصاتی پرکاربرد، تحت عنوان مختصات قطبی را معرفی کنیم.

بیان نقطه در مختصات قطبی

همان‌طور که احتمالا می‌دانید،‌ در دستگاه مختصات کارتزینی، فاصله افقی تا محور y را x و فاصله عمودی تا محور x را y می‌نامند. در شکل زیر این فواصل نشان داده شده‌اند.

فیلم آموزش ریاضی مهندسی در فرادرس

کلیک کنید

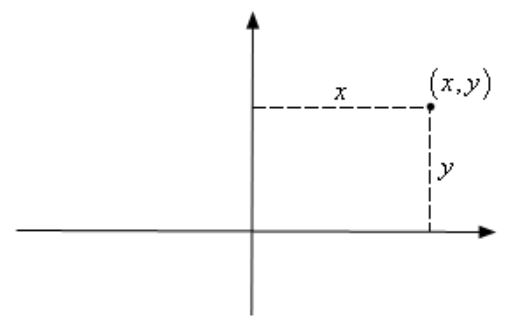
از طرفی می‌توان نقطه بالا را به شکلی متفاوت نیز نشان داد. در این روش مختصات نقطه را با استفاده از دو پارامتر نشان می‌دهند. این دو پارامتر، فاصله از مرکز مختصات و زاویه با محور افقی هستند. در شکل زیر مختصات قطبی نقطه، فاصله و زاویه آن نشان داده شده‌اند.

برای نمونه مختصات دو نقطه‌ی نشان داده شده در شکل زیر به‌ترتیب برابر با $$(2,\pi /6)$$ و $$(2,7\pi /6)$$ هستند. همان‌طور که احتمالا متوجه شده‌اید، عدد سمت چپ، فاصله از مبدا مختصات و عدد سمت راست، زاویه خط متصل‌کننده مبدا و نقطه، با محور افقی است. توجه داشته باشید که زمانی r و θ هم‌علامت هستند که هر دو در یک ربع قرار گیرند. برای نمونه در شکل زیر نقطه مربوط به خط‌چین را می‌توان به‌صورت $$(2,7\pi /6)$$ نیز بیان کرد. در حقیقت در این حالت زاویه و اندازه به‌شکل زیر در نظر گرفته ‌شده‌اند.

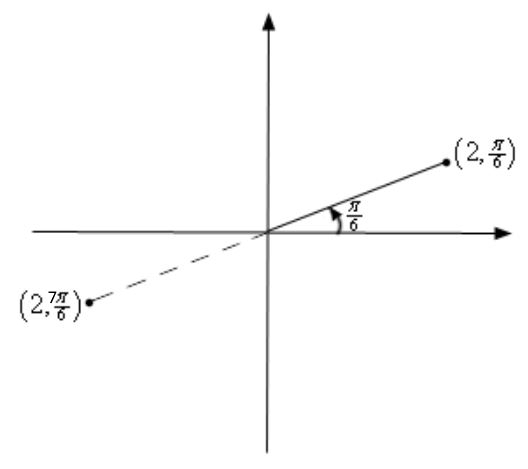
در حالت کلی یک نقطه در دستگاه مختصات قطبی را می‌توان به ۴ طریق بیان کرد. برای نمونه نقطه‌‌ی زیر را در نظر بگیرید.

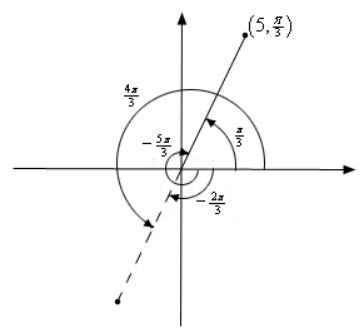
همان‌طور که در شکل بالا نیز مشخص شده زاویه این نقطه با محور افقی برابر با ۶۰ درجه و فاصله نقطه تا مبدا برابر با ۵ است. از این رو مختصات نقطه فوق برابر با $$(5,\pi /3)$$ در نظر گرفته می‌شود. اما در حالت کلی نقطه‌ی مفروض را می‌توان به فرم‌های زیر نمایش داد.

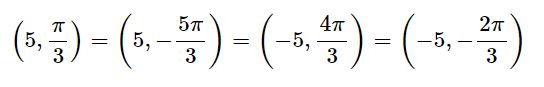
همان‌طور که می‌دانید اگر هر زاویه‌ای را با ۳۶۰ درجه ($$2\pi$$) جمع کنیم، دایره را یک دور زده و به مکان اولیه می‌رسیم. در نتیجه مختصات (r,θ) برابر با $$(r,\theta+2\pi)$$ است.

تبدیل مختصات قطبی و کارتزینی به یکدیگر

در شکل زیر یک نقطه در دو مختصات قطبی و کارتزینی نشان داده شده است.

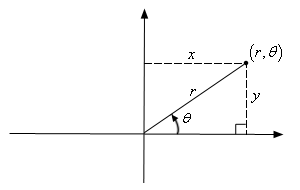
با توجه به این شکل و مفاهیم مثلثات، مختصات x و y را می‌توان بر حسب r و θ، به شکل زیر بیان کرد.

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

البته گاهی اوقات یک معادله یا نقطه در دستگاه مختصاتی قطبی بیان شده و نیاز است آن را در مختصات کارتزینی بیان کنیم. با توجه به عبارت‌های x و y ارائه شده در رابطه بالا، اندازه r برابر است با:

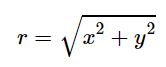
هم‌چنین با تقسیم کردن عبارت‌های x و y به یکدیگر داریم:

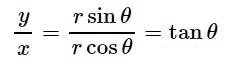
در نتیجه زاویه مختصات قطبی بر حسب مختصاتِ کارتزینی با استفاده از رابطه زیر بدست می‌آید.

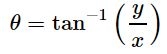
توجه داشته باشید که در رابطه بالا مقدار زاویه در بازه‌ی $$-\pi/2<\theta < \pi/2$$ بیان می‌شود. معمولا راحت‌تر آن است که همواره مقدار r، مثبت بیان شود. نهایتا مختصات کارتزینی را می‌توان با استفاده از رابطه زیر بر حسب مختصات قطبی بیان کرد:

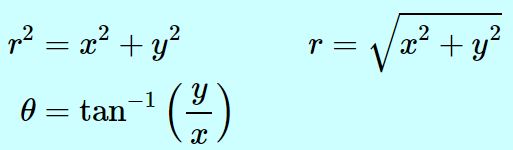
برای درک بهتر به مثالی که در ادامه آمده توجه فرمایید.

مثال ۱

1. $$(-4,2\pi/3) $$ را در مختصات کارتزینی بیان کنید.
2. (۱-,۱-) در مختصات قطبی به چه صورت است.

(۱): با استفاده از رابطه ۱، مختصات x و y برابرند با:

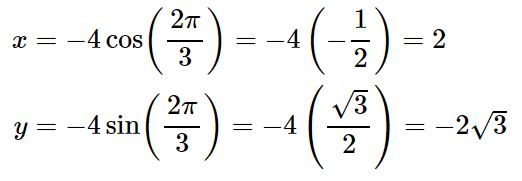
در نتیجه مختصات نقطه $$(-4,2\pi/3) $$ در دستگاه کارتزینی برابر با $$(2,-2\sqrt{3}) $$ است.

(۲): جهت بدست آوردن مختصات قطبی نیز می‌توان از رابطه ۲ استفاده کرد. با قرار دادن ۱- به‌جای مقادیر x و y در رابطه ۲، داریم:

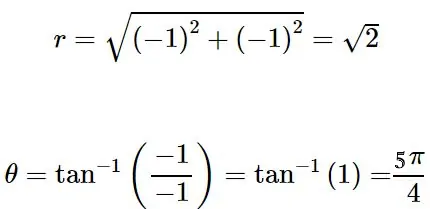
در نتیجه مختصات (۱-,1-) در دستگاه کارتزینی برابر با $$(\sqrt2,5\pi/4) $$ در دستگاه قطبی است.

مثال ۲

1. رابطه $$2x-5x^3=1+xy$$ را در مختصات قطبی بیان کنید.
2. رابطه r=-8cos θ را بر حسب x و y، در مختصات کارتزینی بنویسید.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

(۱): جهت بیان کردن رابطه کارتزینی بر حسب قطبی، کافی است از تبدیل x=rcos θ و y=rsin θ استفاده کنید [این تبدیل همان رابطه ۱ است]. با جایگذاری تبدیل مذکور داریم:

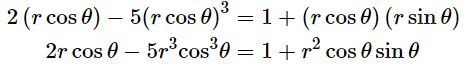
رابطه بالا بر حسب r و θ بیان شده بنابراین رابطه مذکور در دستگاه قطبی بیان شده است.

(۲): با جایگذاری r²=x²+y² در صورت سوال، رابطه ارائه شده در مختصات قطبی به‌شکل زیر بدست می‌آید.

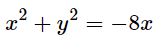
با توجه به مطلب معادله دایره، رابطه بالا نشان دهنده یک دایره است، چراکه با اضافه کردن ۱۶ به طرفینِ رابطه و مرتب کردن، می‌توان آن را به‌صورت زیر بازنویسی کرد.

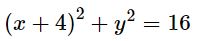
مرکز این دایره در مختصات (4,0-) و اندازه شعاع دایره مذکور برابر با ۴ است. انیمشین زیر مراحل تبدیل شدن یک نمودار از مختصات کارتزینی به قطبی را نشان می‌دهد. در مرحله اولِ حرکت، تابع در مختصات کارتزینی معکوس شده، پس از آن محور x به‌شکل زاویه‌ای در می‌آید.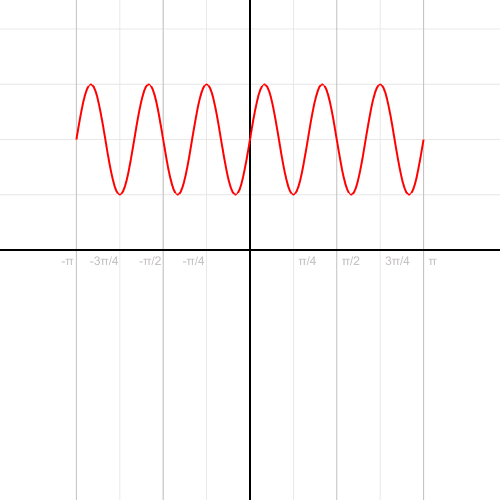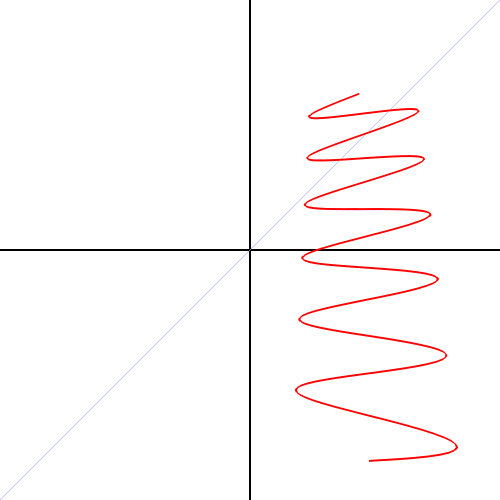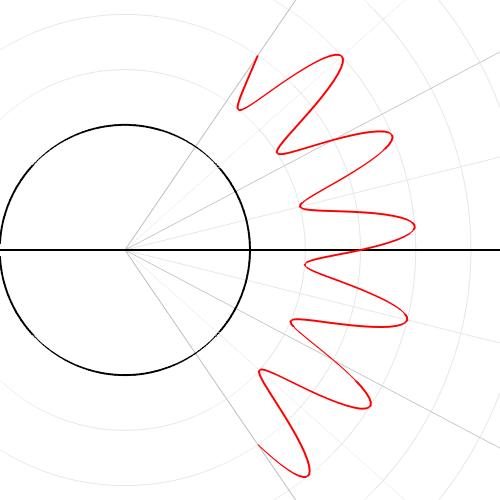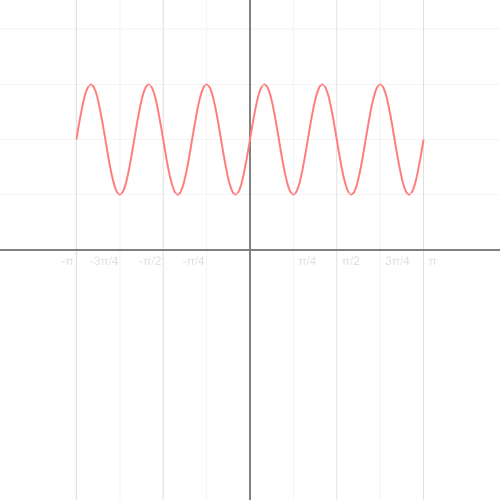

نمودار‌های پرکاربرد در مختصات قطبی

در این قسمت برخی از نمودار‌های شناخته شده در مختصات کارتزینی را در مختصات قطبی بیان خواهیم کرد.

۱. θ=β

فیلم آموزش ریاضیات مهندسی – حل سوالات کنکور ارشد و دکتری در فرادرس

کلیک کنید

رابطه بالا شکل یک منحنی را در مختصات قطبی نشان می‌دهد. در این رابطه θ متغیر و مقدار β، عددی ثابت است. جهت درک شکل نمودار این رابطه بهتر است آن را در مختصات کارتزینی بیان کنیم. از این رو از رابطه ۲ استفاده می‌کنیم. بنابراین با استفاده از رابطه ۲ داریم:

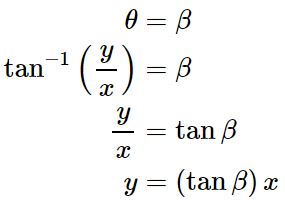
عبارت tan β عددی ثابت است. از این رو رابطه θ=β خطی با شیب ثابت tan β را نشان می‌دهد. شکل زیر چنین نموداری را نشان می‌دهد.

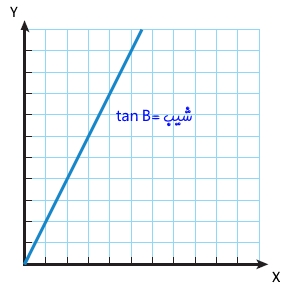
2. r=2a cosθ

جهت بیان کردن رابطه بالا در مختصات کارتزینی، بایستی طرفین رابطه را ابتدا در r ضرب کرد. با انجام این کار داریم:

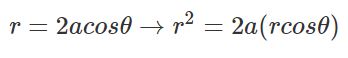
مطابق با رابطه ۱، rcos θ در معادله بالا برابر با x است. در نتیجه رابطه بالا را می‌توان به‌صورت زیر بازنویسی کرد.

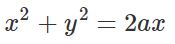
با اضافه کردن عبارت a² به طرفین معادله بالا داریم:

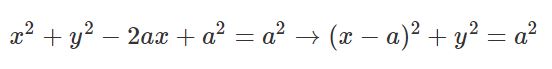
رابطه بالا دایره‌ای به شعاع a و مرکز (a,0) را نشان می‌دهد.

3. r=2b sinθ

مشابه با حالت قبل می‌توان اثبات کرد که این رابطه نیز نشان دهنده تابعی به مرکز $$(0,b)$$ و شعاع b است. البته بهتر است به‌جای حفظ کردن رابطه مربوط به هر نمودار، روش تبدیل مختصات‌ها به یکدیگر را تمرین کنید.

مثال 3

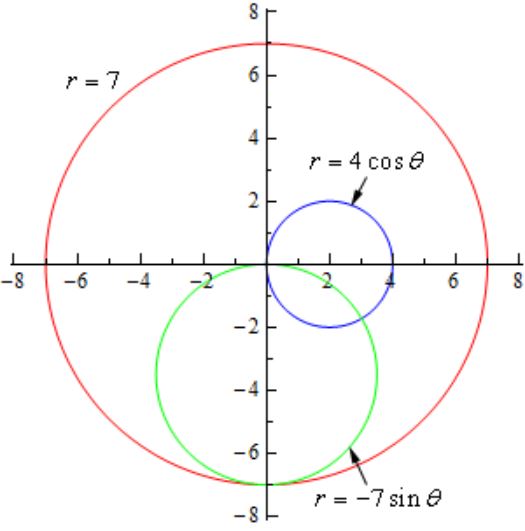
نمودار‌های زیر را در یک دستگاه مختصات x-y رسم کنید.

1. r=7
2. r=4cos θ
3. r=-7sin θ

همان‌طور که می‌دانید رابطه r=7 نشان دهنده دایره‌ای به شعاع ۷ است. از طرفی روابط b و c به‌ترتیب نشان دهنده دایره‌هایی به شعاع‌های ۲ و ۳.۵ هستند. در شکل زیر هر سه‌ نمودار رسم شده‌اند.

مختصات قطبی مبحث مهمی در رشته‌های ریاضیات، علوم پایه و مهندسی محسوب می‌شود و کاربرد زیادی در تعیین مختصات استوانه‌ای نیز دارد. بسیاری از معادلات مرتبط با پدیده‌های فیزیکی را می‌توان در این دستگاه مختصات بیان کرده و حل آن‌ها را آسان‌تر کرد.