مشتق تانژانت – محاسبه و فرمول مشتق tan + مثال و تمرین
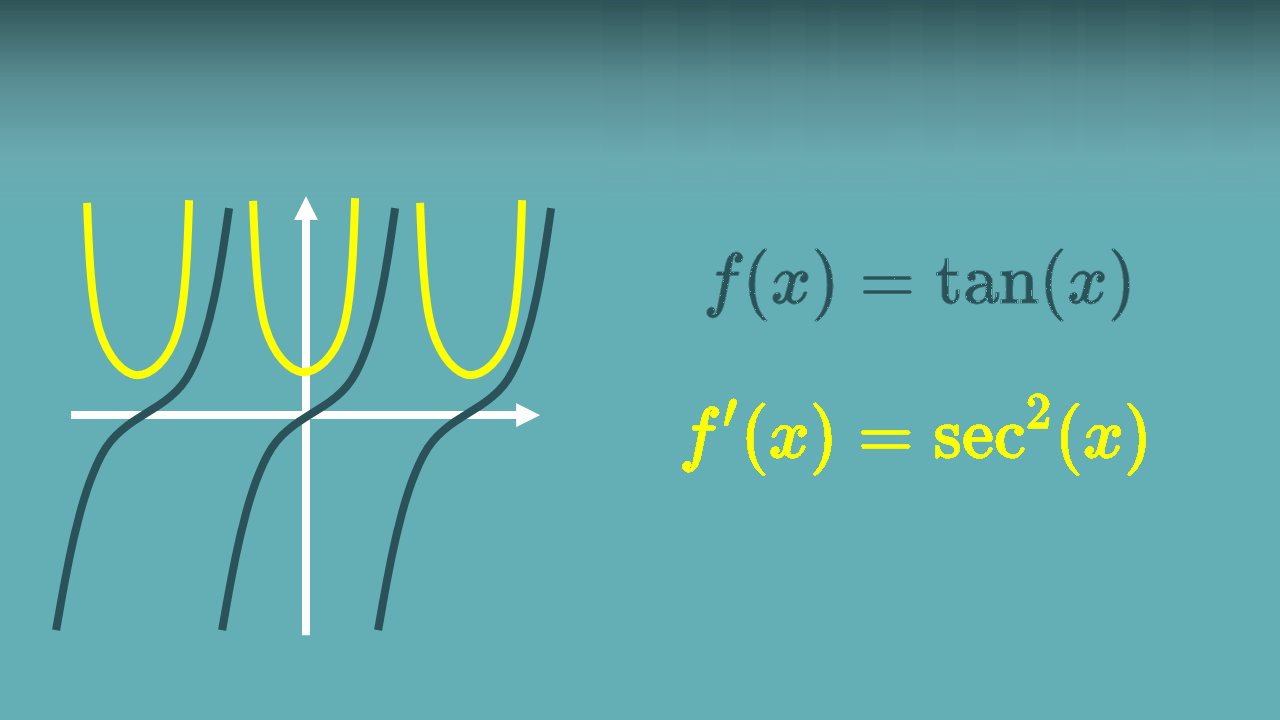
مشتق تانژانت (مشتق tan)، برابر با مربع سکانت (sec۲) است. تانژانت، به عنوان یکی از توابع مثلثاتی اصلی شناخته میشود. این تابع، نسبت سینوس به کسینوس را نمایش میدهد. تانژانت، کاربردهای زیادی در علوم مهندسی و ریاضی دارد. مشتق تانژانت، شیب خط مماس بر منحنی این تابع است. فرمولهای متعددی برای تعیین مشتق تانژانت و دیگر توابع مرتبط با آن (مانند تانژانت تواندار، ضرب تانژانت، تقسیم تانژانت، تانژانت وارون، تانژانت هیپربولیک و غیره) وجود دارد. در این مقاله، به معرفی و اثبات فرمول مشتق تانژانت و توابع مرتبط با آن میپردازیم. علاوه بر این، چندین مثال و تمرین متنوع را نیز حل میکنیم.
تانژانت چیست ؟
«تانژانت» (Tangent)، یکی از سه تابع مثلثاتی اصلی است. توابع مثلثاتی، بر اساس رابطه بین ضلعها و زاویههای حاده مثلث قائمازاویه تعریف میشوند.
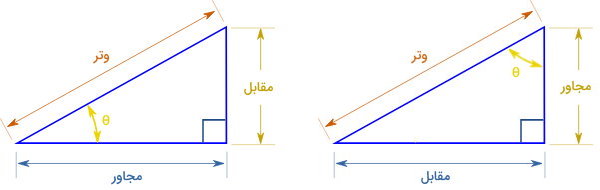
مثلثهای زیر را در نظر بگیرید. نسبت ضلع مقابل به مجاور، تانژانت زاویه θ را نمایش میدهد.
مفهوم مشتق tan چیست ؟
مشتق تانژانت، شیب خط مماس بر منحنی این تابع در یک نقطه دلخواه است.
تصویر زیر، منحنی تابع $$ y = \tan ( \theta ) $$ را در بازه $$ - \frac { ۳ \pi } { ۲ } $$ تا $$ \frac { ۳ \pi } { ۲ } $$ نشان میدهد.
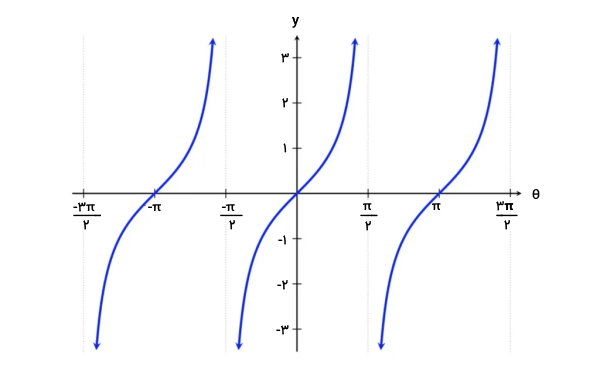
اگر خطی را در نقطه $$ \theta = ۰ $$ بر منحنی تانژانت مماس کنیم، شیب خط برابر با ۰ میشود. بنابراین میگوئیم مشتق تانژانت تتا در نقطه $$ \theta = ۰ $$ برابر با ۰ است. مشتق، به روشهای مختلفی نشان داده میشود. برخی از علائم و عبارتهای جبری مورد استفاده برای نمایش مشتق تانژانت عبارت هستند از:
$$
\frac { d } { d x } \tan ( x )
$$
$$
\tan ^ { \prime } ( x )
$$
$$
( \tan ( x ) ) ^ { \prime }
$$
فرمول مشتق تانژانت چیست ؟
مشتق تانژانت برابر با مربع سکانت است. فرمول مشتق tan به صورت زیر نوشته میشود:
$$
\frac { d } { d x } \tan ( x ) = \sec ^ { ۲ } ( x )
$$
$$
\tan ^ { \prime } ( x ) = \sec ^ { ۲ } ( x )
$$
$$
( \tan ( x ) ) ^ { \prime } = \sec ^ { ۲ } ( x )
$$
مثال ۱: محاسبه تانژانت زاویه ۶۰ درجه
مشتق تابع $$ f ( x ) = \tan ( x ) $$ را در نقطه $$ x = \frac { \pi } { ۳ } $$ را به دست بیاورید.
فرمول محاسبه مشتق tan x عبارت است از:
$$
\frac { d } { d x } \tan ( x ) = \sec ^ { ۲ } ( x )
$$
بنابراین:
$$
f ^ { \prime } ( x ) = \sec ^ { ۲ } ( x )
$$
به جای x، زاویه $$\frac { \pi } { ۳ } $$ (زاویه ۶۰ درجه) را قرار میدهیم:
$$
f ^ { \prime } \left ( \frac { \pi } { ۳ } \right ) = \sec ^ { ۲ } \left ( \frac { \pi } { ۳ } \right )
$$
میدانیم که سکانت یک زاویه، عکس کسینوس آن زاویه را نمایش میدهد. از اینرو، داریم:
$$
\sec \left ( \frac { \pi } { ۳ } \right ) = \frac { ۱ } { \cos \left ( \frac { \pi } { ۳ } \right ) }
$$
$$
\sec ^ ۲ \left ( \frac { \pi } { ۳ } \right ) = \frac { ۱ } { \cos ^ ۲ \left ( \frac { \pi } { ۳ } \right ) }
$$
کسینوس زاویه ۶۰ درجه برابر با $$ \frac{ ۱ } { ۲ } $$ است. از اینرو:
$$
\sec ^ ۲ \left ( \frac { \pi } { ۳ } \right ) = \frac { ۱ } { \left ( \frac { ۱ } { ۲ } \right ) ^ ۲ }
$$
$$
\sec ^ ۲ \left ( \frac { \pi } { ۳ } \right ) = \frac { ۱ } { \frac { ۱ } { ۴ } }
$$
$$
\sec ^ ۲ \left ( \frac { \pi } { ۳ } \right ) = ۴
$$
به این ترتیب:
$$
\frac { d } { d x } \tan \left ( \frac { \pi } { ۳ } \right ) = ۴
$$
در نتیجه، مشتق تانژانت ایکس در زاویه ۶۰ درجه برابر با ۴ است.
اثبات مشتق تانژانت
روشهای مختلفی برای اثبات فرمول مشتق tan x وجود دارد. در این بخش، به معرفی دو روش اصلی اثبات این فرمول میپردازیم.
اثبات مشتق tan با استفاده از فرمول کلی مشتق
اصلیترین روش اثبات مشتق تانژانت، استفاده از رابطه کلی مشتق است. تصویر زیر را در نظر بگیرید. این تصویر، خط مماس بر یک منحنی با تابع f(x) را نمایش میدهد.
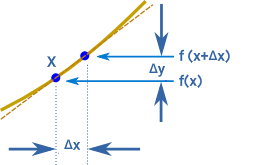
بر اساس تعریف، مشتق تابع f(x)، شیب خط مماس بر منحنی این تابع در نقطه x است. این تعریف، با فرمول زیر و مفهوم حد بیان میشود:
$$
\dfrac { d } { d x } f ( x ) = \lim \limits _ { \Delta x \to ۰ } \dfrac { f ( x + \Delta x ) - f ( x ) } { \Delta x }
$$
برای شروع، تابع تانژانت را درون فرمول بالا قرار میدهیم:
$$
\dfrac { d } { d x } \tan ( x ) = \lim \limits _ { \Delta x \to ۰ } \dfrac { \tan ( x + \Delta x ) - \tan ( x ) } { \Delta x }
$$
میدانیم که:
$$ \tan ( x ) = \frac { \sin ( x ) } { \cos ( x ) } $$
بنابراین:
$$
\dfrac { d } { d x } \tan ( x ) = \lim \limits _ { \Delta x \to ۰ } \dfrac { \frac { \sin ( x + \Delta x ) }{ \cos ( x + \Delta x ) } - \frac { \sin ( x ) }{ \cos ( x ) } } { \Delta x }
$$
$$
\dfrac { d } { d x } \tan ( x ) = \lim \limits _ { \Delta x \to ۰ } \frac { ۱ } { \Delta x } \left ( \frac { \sin ( x + \Delta x ) }{ \cos ( x + \Delta x ) } - \frac { \sin ( x ) }{ \cos ( x ) } \right )
$$
از کسرهای درون پرانتز، مخرج مشترک میگیریم:
$$
\dfrac { d } { d x } \tan ( x ) = \lim \limits _ { \Delta x \to ۰ } \frac { ۱ } { \Delta x } \left ( \frac { \sin ( x + \Delta x ) \cos ( x ) - \cos ( x + \Delta x ) \sin ( x ) }{ \cos ( x + \Delta x ) \cos ( x ) }\right )
$$
بر اساس قانون تفریق زوایا در مثلثات میتوانیم صورت کسر را ساده کنیم. این قانون به صورت زیر نوشته میشود:
$$ \sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta $$
اگر $$ x + \Delta x $$ را برابر با $$ \alpha $$ و $$ x $$ را برابر با $$ \beta $$ در نظر بگیریم، خواهیم داشت:
$$
\sin ( x + \Delta x ) \cos ( x ) - \cos ( x + \Delta x ) \sin ( x ) = \sin ( x + \Delta x - x )
$$
$$
\sin ( x + \Delta x ) \cos ( x ) - \cos ( x + \Delta x ) \sin ( x ) = \sin ( \Delta x )
$$
این رابطه را درون حد جایگذاری میکنیم:
$$
\dfrac { d } { d x } \tan ( x ) = \lim \limits _ { \Delta x \to ۰ } \frac { ۱ } { \Delta x } \left ( \frac { \sin ( \Delta x ) }{ \cos ( x + \Delta x ) \cos ( x ) }\right )
$$
$$ \sin ( \Delta x ) $$ را به صورت کسر بیرونی انتقال میدهیم:
$$
\dfrac { d } { d x } \tan ( x ) = \lim \limits _ { \Delta x \to ۰ } \frac { \sin ( \Delta x ) } { \Delta x } \left ( \frac { ۱ }{ \cos ( x + \Delta x ) \cos ( x ) }\right )
$$
اکنون، عبارت حدی را به صورت ضرب دو حد جداگانه مینویسیم:
$$
\dfrac { d } { d x } \tan ( x ) = \lim \limits _ { \Delta x \to ۰ } \frac { \sin ( \Delta x ) } { \Delta x } \cdot \lim \limits _ { \Delta x \to ۰ } \frac { ۱ }{ \cos ( x + \Delta x ) \cos ( x ) }
$$
حد $$ \lim _ { \Delta x \to ۰ } \frac { \sin ( \Delta x ) }{ \Delta x } $$، با استفاده از قضیه فشردگی اثبات میشود. این حد عبارت است از:
$$
\lim _ { \Delta x \to ۰ } \frac { \sin ( \Delta x ) }{ \Delta x } = ۱
$$
جواب حد را درون فرمول مشتق قرار میدهیم:
$$
\dfrac { d } { d x } \tan ( x ) = ۱ \times \lim \limits _ { \Delta x \to ۰ } \frac { ۱ }{ \cos ( x + \Delta x ) \cos ( x ) }
$$
$$
\dfrac { d } { d x } \tan ( x ) = \lim \limits _ { \Delta x \to ۰ } \frac { ۱ }{ \cos ( x + \Delta x ) \cos ( x ) }
$$
با قرار دادن ۰ به جای $$ \Delta x $$، به جواب نهایی میرسیم:
$$
\dfrac { d } { d x } \tan ( x ) = \frac { ۱ }{ \cos ( x + ۰ ) \cos ( x ) }
$$
$$
\dfrac { d } { d x } \tan ( x ) = \frac { ۱ }{ \cos ( x ) \cos ( x ) }
$$
$$
\dfrac { d } { d x } \tan ( x ) = \frac { ۱ }{ \cos ^ ۲ ( x ) }
$$
میدانیم که عکس نسبت کسینوس، به عنوان سکانت تعریف میشود. در نتیجه:
$$
\dfrac { d } { d x } \tan ( x ) = \sec ^ ۲ ( x )
$$
به این ترتیب، فرمول مشتق تانژانت را اثبات کردیم. دیگر روشهای اثبات مشتق tan، بر مبنای قوانین مشتقگیری و مشتق توابع مثلثاتی هستند. در ادامه، به توضیح یکی از این روشها میپردازیم.
اثبات مشتق tan با استفاده از فرمول مشتق تقسیم دو تابع
تابع تانژانت به صورت تقسیم تابع سینوس بر کسینوس نوشته میشود:
$$ \tan ( x ) = \frac { \sin ( x ) }{ \cos ( x ) } $$
بنابراین، به منظور اثبات مشتق تانژانت میتوانیم از تقسیم دو تابع سینوس و کسینوس مشتق بگیریم:
$$ \frac { d } { d x } \tan ( x ) = \frac { d } { d x } \left ( \frac { \sin ( x ) }{ \cos ( x ) } \right ) $$
مشتق تقسیم دو تابع، از فرمول زیر به دست میآید:
$$
\left ( \frac { u }{ v } \right ) ^ { \prime } = \frac {v u ^ { \prime } - u v ^ { \prime } } { v ^ ۲ }
$$
برای استفاده از این فرمول، تغییر متغیرهای زیر را انجام میدهیم:
$$ u ( x ) = \sin ( x ) $$
$$ v ( x )= \cos ( x ) $$
مشتق سینوس برابر کسینوس و مشتق کسینوس برابر با منفی سینوس است. به این ترتیب:
$$ u ^ { \prime } ( x ) = \cos ( x ) $$
$$ v ^ { \prime } ( x ) = - \sin ( x ) $$
با جایگذاری توابع u و v به همراه مشتقهایشان درون فرمول مشتق تقسیم دو تابع، داریم:
$$
\left ( \frac { \sin ( x ) }{ \cos ( x ) } \right ) ^ { \prime } = \frac { \cos ( x ) \cos ( x ) + \sin ( x ) \sin ( x ) } { \cos ^ ۲ ( x ) }
$$
$$
\left ( \frac { \sin ( x ) }{ \cos ( x ) } \right ) ^ { \prime } = \frac { \cos ^ ۲ ( x ) + \sin ^ ۲ ( x ) } { \cos ^ ۲ ( x ) }
$$
جمع مربعات سینوس و کسینوس برابر با ۱ است:
$$
\left ( \frac { \sin ( x ) }{ \cos ( x ) } \right ) ^ { \prime } = \frac { ۱ } { \cos ^ ۲ ( x ) }
$$
$$
\left ( \frac { \sin ( x ) }{ \cos ( x ) } \right ) ^ { \prime } = \sec ^ ۲ ( x )
$$
$$
( \tan ( x ) ) ^ { \prime } = \sec ^ ۲ ( x )
$$
به این ترتیب، فرمول مشتق tan اثبات میشود.
فرمول کلی مشتق تانژانت
فرم کلی تابع تانژانت عبارت است از:
$$ f ( x ) = a \tan ( b x + c ) $$
a و b، ضرایب عددی بوده و c، ثابت عددی است. بر اساس این تابع، فرمول کلی مشتق تانژانت به صورت زیر نوشته میشود:
$$ ( a \tan ( b x + c ) ) ^ { \prime } = ab \sec ^ ۲ ( b x + c ) $$
مثال ۲: محاسبه مشتق تانژانت
مشتق $$ y = ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) $$ را در نقطه $$ x = \frac { \pi } { ۱۲ } $$ به دست بیاورید.
برای حل این مثال، ابتدا فرمول کلی مشتق tan را مینویسیم:
$$ ( a \tan ( b x + c ) ) ^ { \prime } = ab \sec ^ ۲ ( b x + c ) $$
با توجه به صورت سوال، داریم:
$$ a = ۵ $$
$$ b = ۲ $$
$$ c = \frac { \pi } { ۸ } $$
بنابراین:
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = ۵ \times ۲ \sec ^ ۲ \left ( ۲ x + \frac { \pi }{ ۱۲ } \right )
$$
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = ۱۰ \sec ^ ۲ \left ( ۲ x + \frac { \pi }{ ۱۲ } \right )
$$
به این ترتیب، رابطه مشتق y را به دست آوردیم. اکنون، مقدار عددی x را درون جواب جایگذاری میکنیم:
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = ۱۰ \sec ^ ۲ \left ( ۲ \times \frac { \pi }{ ۱۲ } + \frac { \pi }{ ۱۲ } \right )
$$
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = ۱۰ \sec ^ ۲ \left ( \frac { \pi }{ ۶ } + \frac { \pi }{ ۱۲ } \right )
$$
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = ۱۰ \sec ^ ۲ \left ( \frac { ۲ \pi }{ ۱۲ } + \frac { \pi }{ ۱۲ } \right )
$$
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = ۱۰ \sec ^ ۲ \left ( \frac { ۳ \pi }{ ۱۲ } \right )
$$
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = ۱۰ \sec ^ ۲ \left ( \frac { \pi }{ ۴ } \right )
$$
با توجه به رابطه بین سکانت و کسینوس، داریم:
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = \frac { ۱۰ } {\cos ^ ۲ \left ( \frac { \pi }{ ۴ } \right ) }
$$
کسینوس $$ \frac { \pi } { ۴ } $$ یا کسینوس زاویه ۴۵ درجه برابر با $$ \frac { \sqrt { ۲ } } { ۲ } $$ است. بنابراین:
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = \frac { ۱۰ } { \frac { \sqrt { ۲ } } { ۲ } }
$$
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = \frac { ۱۰ } { \left ( \frac { \sqrt { ۲ } } { ۲ } \right ) ^ ۲ }
$$
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = \frac { ۱۰ } { \frac { ۲ } { ۴ } }
$$
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = \frac { ۱۰ } { \frac { ۱ } { ۲ } }
$$
$$
\left ( ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) \right ) ^ { \prime } = ۲۰
$$
در نتیجه، مشتق $$ y = ۵ \tan \left ( ۲ x + \frac { \pi }{ ۱۲ } \right ) $$ در نقطه $$ x = \frac { \pi } { ۱۲ } $$ برابر با ۲۰ است.
مقایسه مشتق تانژانت و کتانژانت
«کتانژانت» (Cotangent)، یکی دیگر از توبع مثلثاتی معروف است. این تابع، به عنوان عکس نسبت تانژانت شناخته میشود. به عبارت دیگر، در یک مثلث قائمالزاویه با زاویه حاده θ، کتانژانت θ، تقسیم ضلع مجاور θ بر ضلع مقابل θ است.
تصویر زیر، نمودار توابع tan(x) و cot(x) در بازه ۰ تا ۳۶۰ درجه را نمایش میدهد.

مشتق کتانژانت نیز مانند مشتق تانژانت، شیب مماس بر منحنی تابع است. فرمول مشتق cot به صورت زیر نوشته میشود:
$$
\frac { d } { d x } \cot ( x ) = - \csc ^ ۲ ( x )
$$
مشتق کتانژانت، منفی مربع کسکانت است. با توجه به رابطه بین کسکانت و سینوس، مشتق کتانژانت از فرمول زیر نیز به دست میآید:
$$
\frac { d } { d x } \cot ( x ) = - \frac { ۱ } { \sin ^ ۲ ( x ) }
$$
مثال ۳: محاسبه مشتق جمع تانژانت و کتانژانت
مشتق $$ f ( x ) = \tan ( x ) + \cot ( x ) $$ را در زاویه ۶۰ درجه محاسبه کنید.
تابع f(x)، جمع دو تابع مثلثاتی است. بر اساس قوانین مشتقگیری، مشتق جمع دو تابع با جمع مشتق هر یک از توابع برابری میکند. این قانون به صورت زیر نوشته میشود:
$$ ( g ( x ) + h ( x ) ) ^ { \prime } = g ^ { \prime } ( x ) + f ^ { \prime } ( x ) $$
بنابراین:
$$
f ^ { \prime } ( x ) = \frac { d } { d x } \left [ \tan ( x ) + \cot ( x ) \right ] = \frac { d } { d x } \tan ( x ) + \frac { d } { d x } \cot ( x )
$$
با توجه به فرمول مشتق تانژانت و کتانژانت، میدانیم:
$$
\frac { d } { d x } \tan ( x ) = \sec ^ ۲ ( x )
$$
$$
\frac { d } { d x } \cot ( x ) = - \csc ^ ۲ ( x )
$$
به این ترتیب، داریم:
$$
f ^ { \prime } ( x ) = \frac { d } { d x } \left [ \tan ( x ) + \cot ( x ) \right ] = \sec ^ ۲ ( x ) - \csc ^ ۲ ( x )
$$
اکنون، متغیر x را برابر با زاویه ۶۰ درجه یا $$ \frac { \pi } { ۳ } $$ قرار میدهیم:
$$
f ^ { \prime } ( x ) = \frac { d } { d x } \left [ \tan ( x ) + \cot ( x ) \right ] = \sec ^ ۲ \left ( \frac { \pi } { ۳ } \right ) - \csc ^ ۲ \left ( \frac { \pi } { ۳ } \right )
$$
سکانت ۶۰ درجه برابر با ۲ و کسکانت ۶۰ درجه برابر با $$ \frac { ۲ } { \sqrt { ۳ } } $$ است. در نتیجه:
$$
f ^ { \prime } ( x ) = \frac { d } { d x } \left [ \tan ( x ) + \cot ( x ) \right ] = \left ( ۲ \right ) ^ ۲ - \left ( \frac { ۲ } { \sqrt { ۳ } } \right ) ^ ۲
$$
$$
f ^ { \prime } ( x ) = \frac { d } { d x } \left [ \tan ( x ) + \cot ( x ) \right ] = ۴ - \frac { ۴ } { ۳ }
$$
$$
f ^ { \prime } ( x ) = \frac { d } { d x } \left [ \tan ( x ) + \cot ( x ) \right ] = \frac { ۱۲ - ۴ } { ۳ }
$$
$$
f ^ { \prime } ( x ) = \frac { d } { d x } \left [ \tan ( x ) + \cot ( x ) \right ] = \frac { ۸ } { ۳ }
$$
$$
f ^ { \prime } ( x ) = \frac { ۸ } { ۳ }
$$
بنابراین، مشتق مجموع تانژانت و کتانژانت در زاویه ۶۰ درجه برابر با هشتسوم است.
مشتق تانژانت توان دار
در بخشهای قبلی، فرمول کلی مشتق تانژانت با توان ۱ را معرفی کردیم. برای تابع tan با توانهای دیگر، رابطه محاسبه مشتق تغییر میکند.
تابع تانژانت به توان n را در نظر بگیرید:
$$ f ( x ) = \tan ^ { n } ( x ) $$
مشتق این تابع، از رابطه زیر به دست میآید:
$$
f ^ { \prime } ( x ) = n \sec ^ ۲ ( x ) \tan ^ { n - ۱ } ( x )
$$
n میتواند یک عدد مثبت یا منفی باشد. در ادامه، نحوه استفاده از این فرمول برای محاسبه مشتق tan به توان n را با حل چند مثال توضیح میدهیم.
مثال ۴: محاسبه مشتق تانژانت به توان ۲
مشتق تابع tan به توان ۲ را به دست بیاورید.
برای به دست آوردن مشتق $$ \tan ^ ۲ ( x ) $$، دو روش اصلی وجود دارد. روش اول، استفاده از قانون ضرب در مشتقگیری است. بر اساس این قانون، مشتق ضرب تابع f(x) در تابع g(x) برابر است با:
$$ \frac { d } { d x } [ f ( x ) g ( x ) ] = f ( x ) g ' ( x ) + g ( x ) f ' ( x ) $$
برای استفاده از فرمول بالا، $$ \tan ^ ۲ ( x ) $$ را به صورت ضرب تابع تانژانت در خودش مینویسیم:
$$ \tan ^ ۲ ( x ) = \tan ( x ) \cdot \tan ( x ) $$
یکی از تانژانتها را برابر با f(x) و دیگری را برابر با g(x) قرار میدهیم:
$$ f ( x ) = \tan ( x ) $$
$$ g ( x ) = \tan ( x ) $$
مشتق این توابع برابر هستند با:
$$
f ^ { \prime } ( x ) = \sec ^ ۲ ( x )
$$
$$
g ^ { \prime } ( x ) = \sec ^ ۲ ( x )
$$
توابع f(x) و g(x) را به همراه مشتقهایشان درون فرمول مشتق ضرب دو تابع قرار میدهیم:
$$
\frac { d } { d x } [ f ( x ) g ( x ) ] = f ( x ) g ' ( x ) + g ( x ) f ' ( x )
$$
$$
\frac { d } { d x } [ \tan ( x ) \cdot \tan ( x ) ] = \tan ( x ) \sec ^ ۲ ( x ) + \tan ( x ) \sec ^ ۲ ( x )
$$
$$
\frac { d } { d x } \tan ^ ۲ ( x ) = ۲ \tan ( x ) \sec ^ ۲ ( x )
$$
به این ترتیب، مشتق تانژانت به توان دو را به دست آوردیم. روش دوم حل این مشتق، استفاده از فرمول کلی مشتق تانژانت تواندار است. این فرمول به صورت زیر نوشته میشود:
$$
f ^ { \prime } ( x ) = n \sec ^ ۲ ( x ) \tan ^ { n - ۱ } ( x )
$$
توان تانژانت در صورت سوال برابر با ۲ (یعنی $$ n = ۲ $$) است. با قرار دادن این عدد در رابطه بالا، خواهیم داشت:
$$
f ^ { \prime } ( x ) = ۲ \sec ^ ۲ ( x ) \tan ^ { ۲ - ۱ } ( x )
$$
$$
f ^ { \prime } ( x ) = ۲ \sec ^ ۲ ( x ) \tan ^ { ۱ } ( x )
$$
$$
f ^ { \prime } ( x ) = ۲ \sec ^ ۲ ( x ) \tan ( x )
$$
همانطور که مشاهده میکنید، با استفاده از فرمول مخصوص، به سرعت جواب مشتق تانژانت تواندار را به دست آوردیم.
مثال ۵: محاسبه تانژانت به توان ۳
مشتق $$ \tan ^ ۳ ( x ) $$ را تعیین کنید.
برای به دست آوردن مشتق مورد سوال، فرمول مشتق تانژانت تواندار را مینویسیم:
$$
f ^ { \prime } ( x ) = n \sec ^ ۲ ( x ) \tan ^ { n - ۱ } ( x )
$$
n (توان تانژانت) برابر با ۳ است. این عدد را در فرمول بالا قرار میدهیم:
$$
f ^ { \prime } ( x ) = ۳ \sec ^ ۲ ( x ) \tan ^ { ۳ - ۱ } ( x )
$$
$$
f ^ { \prime } ( x ) = ۳ \sec ^ ۲ ( x ) \tan ^ { ۲ } ( x )
$$
مثال ۶: محاسبه مشتق تانژانت به توان منفی یک
مشتق تانژانت به توان منفی یک را به دست بیاورید.
تانژانت به توان منفی را در نظر بگیرید:
$$
\left ( \tan ( x ) \right ) ^ { - ۱ }
$$
میتوانیم این تابع را به صورت زیر بازنویسی کنیم:
$$
\left ( \tan ( x ) \right ) ^ { - ۱ } = \frac { ۱ } { \tan ( x ) }
$$
میدانیم که عکس تانژانت برابر با کتانژانت است. بنابراین، مشتق tan به توان منفی ۱ برابر با مشتق کتانژانت میشود. با این وجود، برای این مثال، از فرمول مشتق تقسیم دو تابع استفاده میکنیم. این فرمول، عبارت است از:
$$ \frac { d } { d x } [ \frac { f ( x ) } { g ( x ) } ] = \frac { g ( x ) f' ( x ) - f ( x ) g' ( x ) } { [ g ( x ) ] ^ { ۲ } } $$
f(x) و g(x) را به صورت زیر در نظر میگیریم:
$$ f ( x ) = ۱ $$
$$ g ( x ) = \tan ( x ) $$
مشتق این توابع عبارت هستند از:
$$ f ^ { \prime } ( x ) = ۰ $$
$$ g ^ { \prime } ( x ) = \sec ^ ۲ ( x ) $$
f(x) و g(x) را به همراه مشتق آنها درون فرمول مشتق تقسیم دو تابع قرار میدهیم:
$$ \frac { d } { d x } [ \frac { f ( x ) } { g ( x ) } ] = \frac { g ( x ) f' ( x ) - f ( x ) g' ( x ) } { [ g ( x ) ] ^ { ۲ } } $$
$$
\frac { d } { d x } [ \frac { ۱} { \tan ( x ) } ] = \frac { \tan ( x ) \times ۰ - ۱ \times \sec ^ ۲ ( x ) } { [ \tan ( x ) ] ^ { ۲ } }
$$
$$
\frac { d } { d x } [ \frac { ۱} { \tan ( x ) } ] = \frac { ۰ - \sec ^ ۲ ( x ) } { \tan ^ ۲ ( x ) }
$$
$$
\frac { d } { d x } [ \frac { ۱} { \tan ( x ) } ] = - \frac { \sec ^ ۲ ( x ) } { \tan ^ ۲ ( x ) }
$$
سکانت و تانژانت را بر حسب سینوس و کسینوس بازنویسی میکنیم:
$$
\frac { d } { d x } [ \frac { ۱} { \tan ( x ) } ] = - \frac { \frac { ۱ } { \cos ^ ۲ ( x ) } } { \frac { \sin ^ ۲ ( x ) } { \cos ^ ۲ ( x ) } }
$$
$$
\frac { d } { d x } [ \frac { ۱} { \tan ( x ) } ] = - \frac { ۱ } { \sin ^ ۲ ( x ) }
$$
به این ترتیب، داریم:
$$
\frac { d } { d x } [ \frac { ۱} { \tan ( x ) } ] = - \csc ^ ۲ ( x )
$$
در نتیجه، مشتق tan به توان منفی ۱ برابر با منفی مربع کسکانت است. تانژانت به توان منفی یک در این مثال با معکوس تانژانت تفاوت دارد (این دو تابع به یک شکل نمایش داده میشوند). در بخشهای بعدی، به معرفی فرمول مشتق تانژانت معکوس نیز خواهیم پرداخت.
مشتق زنجیره ای تانژانت
قاعده مشتق زنجیرهای، فرمولی است که به منظور مشتقگیری از توابع تو در تو مورد استفاده قرار میگیرد. بر اساس این قاعده، مشتق تابع f(g(x)) از رابطه زیر به دست میآید:
$$ \frac { d } { d x } f \left ( g ( x ) \right ) = f' \left ( g ( x ) \right ) g' (x ) $$
فرم ساده تابع تانژانت به صورت زیر نوشته میشود:
$$ f ( x ) = \tan ( x ) $$
به جای x، تابعی مانند g(x) را در نظر بگیرید:
$$ f ( g ( x ) ) = \tan ( g ( x ) ) $$
با توجه به قاعده زنجیرهای، مشتق تابع تو در توی بالا عبارت است از:
$$
\frac { d } { d x } \tan \left ( g ( x ) \right ) = \sec ^ ۲ \left ( g ( x ) \right ) g' ( x )
$$
مثال ۷: محاسبه مشتق تانژانت u
تابع f(u) را در نظر بگیرید:
$$ f ( u ) = \tan ( u ) $$
اگر $$ u = ۳ x ^ ۳ - ۹ x + ۸ $$ باشد، مشتق tan(u) چه خواهد بود؟
در صورتی که u، یک تابع باشد، f(u) یک تابع تو در تو خواهد بود. مشتق توابع تو در تو از رابطه زیر به دست میآید:
$$
\frac { d } { d x } f \left ( g ( x ) \right ) = f' \left ( g ( x ) \right ) g' (x )
$$
در رابطه بالا، u را جایگزین g(x) میکنیم:
$$
\frac { d } { d x } f ( u ) = u' f ' ( u )
$$
به این ترتیب، داریم:
$$
\frac { d } { d x } \tan ( u ) = u' \tan ' ( u )
$$
مشتق u برابر است با:
$$ u ^ { \prime } = \left ( ۳ x ^ ۳ - ۹ x + ۸ \right ) ^ { \prime } $$
$$
u ^ { \prime } = ۹ x ^ ۲ - ۹
$$
از طرف دیگر، میدانیم که:
$$
f ^ { \prime } ( u ) = \tan ^ { \prime } ( u ) = \sec ^ ۲ ( u )
$$
$$
\tan ^ { \prime } ( u ) = \sec ^ ۲ ( ۳ x ^ ۳ - ۹ x + ۸ )
$$
با قرار دادن مشتقهای بالا در فرمول اصلی، به جواب زیر میرسیم:
$$
\frac { d } { d x }\tan ( ۳ x ^ ۳ - ۹ x + ۸ ) = \left ( ۹ x ^ ۲ - ۹ \right ) \sec ^ ۲ ( ۳ x ^ ۳ - ۹ x + ۸ )
$$
مشتق تانژانت وارون
توابع وارون، عملکرد توابع را معکوس میکنند. به عنوان مثال، در یک تابع مثلثاتی ساده، با قرار دادن اندازه زاویه به جای متغیر تابع، به یک مقدار عددی میرسیم. از طرف دیگر، در وارون یک تابع مثلثات، با قرار دادن مقدار عددی به جای متغیر تابع، به یک زاویه میرسیم.
تابع تانژانت وارون به صورت زیر نوشته میشود:
$$ \tan ^ { - ۱ } ( x ) = \theta $$
$$
\arctan ( x ) = \theta
$$
به این تابع، تانژانت اینورس، آرکتانژانت و تانژانت معکوس نیز میگویند. مشتق تانژانت معکوس از رابطه زیر به دست میآید:
$$
\frac { d } { d x } \arctan ( x ) = \frac { ۱ } { ۱ + x ^ ۲ }
$$
برای تانژانت وارون $$ \frac { x } { a } $$، داریم:
$$
\frac { d } { d x } \arctan \left ( \frac { x } { a } \right ) = \frac { a } { a ^ ۲ + x ^ ۲ }
$$
اگر یک تابع نظیر u درون تابع تانژانت وارون وجود داشته باشد، فرمول مشتق به صورت زیر نوشته میشود:
$$
\frac { d } { d x } \arctan ( u ) = \frac { u ^ { \prime } } { ۱ + u ^ ۲ }
$$
مثال ۸: محاسبه مشتق تانژانت معکوس
مشتق تانژانت اینورس $$ \frac { ۱ } { x } $$ را به دست بیاورید.
صورت سوال، حاصل عبارت زیر را از ما میخواهد:
$$
\frac { d } { d x } \arctan \left ( \frac { ۱ } { x } \right )
$$
اگر $$ \frac { ۱ } { x } $$ را برابر با u در نظر بگیریم، جواب مشتق arc tan برابر خواهد بود با:
$$
\frac { d } { d x } \arctan ( u ) = \frac { u ^ { \prime } } { ۱ + u ^ ۲ }
$$
با توجه به تغییر متغیر، داریم:
$$ u = \frac { ۱ } { x } $$
$$ u ^ { \prime } = - \frac { ۱ } { x ^ ۲ } $$
این روابط را درون فرمول اصلی مشتق تابع وارون تانژانت جایگذاری میکنیم:
$$
\frac { d } { d x } \arctan ( u ) = \frac { u ^ { \prime } } { ۱ + u ^ ۲ }
$$
$$
\frac { d } { d x } \arctan \left ( \frac { ۱ } { x } \right )
= \frac {- \frac { ۱ } { x ^ ۲ } } { ۱ + \frac { ۱ } { x ^ ۲ } }
$$
پس از سادهسازی صورت و مخرج، به جواب زیر میرسیم:
$$
\frac { d } { d x } \arctan \left ( \frac { ۱ } { x } \right )
=- \frac { ۱ } { x ^ ۲ + ۱ }
$$
مشتق تانژانت هیپربولیک
توابع مثلثاتی، با استفاده از معادله دایره (دایره واحد) تعریف میشوند. توابع هیپربولیک، مشابه توابع مثلثاتی هستند با این تفاوت که تعریف آنها توسط معادله هذلولی صورت میگیرد.
پارامتر اصلی در تعریف توابع هذلولی یا هیپربولیک، عدد اویلر است. تابع تانژانت هیپربولیک ($$ \tanh ( x ) $$) به صورت زیر نوشته میشود:
$$
\tanh ( x ) = \frac { e ^ x - e ^ { - x } }{ e ^ x + e ^ { - x } }
$$
مشتق tanh از رابطه زیر به دست میآید:
$$
\tanh ^ { \prime } ( x ) = \text { sech } ^ ۲ ( x )
$$
به عبارت دیگر:
$$
\tanh ^ { \prime } ( x ) = \frac { ۴ }{ \left ( e ^ x + e ^ { - x } \right ) ^ ۲}
$$
فرمول تانژانت هیپربولیک یک تابع (مانند u)، عبارت است از:
$$
\tanh ^ { \prime } ( u ) = u ^ { \prime } \text { sech } ^ ۲ ( u )
$$
مشتق تانژانت هیپربولیک وارون
توابع هیپربولیک نیز مانند توابع مثلثاتی معمولی، وارون دارند. مشتق وارون تابع tanh از رابطه زیر به دست میآید:
$$
\text { arctanh } ^ { \prime } ( x ) = \frac { ۱ }{ ۱ - x ^ ۲ }
$$
فرمول وارون تانژانت هیپربولیک یک تابع (مانند u)، به صورت زیر نوشته میشود:
$$
\text { arctanh } ^ { \prime } ( x ) = \frac { u ^ { \prime } }{ ۱ - u ^ ۲ }
$$
مثال ۹: محاسبه مشتق تانژانت هیپربولیک
مشتق $$ \tanh ( \ln ( x ) ) $$ را به دست بیاورید.
تابع $$ \tanh ( \ln ( x ) ) $$، یک تابع تو در تو است. برای مشتقگیری از این نوع تابع، عبارت داخل پرانتز را برابر با u در نظر میگیریم:
$$ u = \ln ( x ) $$
مشتق u (مشتق ln) برابر است با:
$$ u ^ { \prime } = \frac { ۱ } { x } $$
اکنون، تابع اصلی را با تغییر متغیر u در نظر میگیریم:
$$ \tanh ( u ) $$
مشتق این تابع از فرمول زیر به دست میآید:
$$
\tanh ^ { \prime } ( u ) = u ^ { \prime } \text { sech } ^ ۲ ( u )
$$
با قرار دادن u و 'u در فرمول بالا، به جواب نهایی میرسیم:
$$
\tanh ^ { \prime } ( \ln ( x ) ) = \frac { ۱ } { x }\text { sech } ^ ۲ ( \ln ( x ) )
$$
$$
\tanh ^ { \prime } ( \ln ( x ) ) = \frac { \text { sech } ^ ۲ ( \ln ( x ) ) } { x }
$$
مشتق مراتب بالاتر تانژانت
منظور از مشتق مراتب بالاتر، تکرار فرآیند مشتقگیری از یک تابع است. به عنوان مثال، در بخشهای قبلی دیدیم که مشتق تانژانت برابر با مربع سکانت میشود. به مربع سکانت، مشتق مرتبه اول تانژانت میگویند.
اگر از مربع سکانت مشتق بگیریم، عبارت به دست آمده، مشتق مرتبه دوم تانژانت خواهد بود. با تکرار همین فرآیند بر روی نتایج مشتقگیری، مشتق مرتبه سوم، مرتبه چهارم و مراتب بالاتر تعیین میشوند. برای تابع $$ y = f ( x ) $$، مشتقهای مرتبه اول و بالاتر به صورت زیر نمایش داده میشوند:
$$
\frac { d y } { d x } , \; \frac { d } { d x } \left ( \frac { d y } { d x } \right ) , \; \frac { d } { d x } \left ( \frac { d } { d x } \left ( \frac { d y } { d x } \right ) \right ) , \; ...
$$
$$
\frac { d y } { d x } , \; \frac { d ^ ۲ y } { d x ^ ۲ } , \; \frac { d ^ ۳ y } { d x ^ ۳ } , \; ...
$$
$$
f ^ { \prime } ( x ) , \; f ^ { \prime \prime } ( x ) , \; f ^ { \prime \prime \prime} ( x ) , \; ...
$$
البته روشهای مختلفی برای نمایش علامت مشتق در ریاضی وجود دارند. با این وجود، علائم بالا، متداولتر هستند. با این تفاصیل، مشتق مرتبه اول تانژانت به صورت زیر نوشته میشود:
$$
\frac { d } { d x } \tan ( x ) = \sec ^ ۲ ( x )
$$
برای مشتق مرتبه دوم تانژانت، داریم:
$$
\frac { d ^ ۲ } { d x ^ ۲ } \tan ( x ) = \frac { d } { d x } \sec ^ ۲ ( x ) = ۲ \tan ( x ) \sec ^ ۲ ( x )
$$
به دست آوردن مشتق مراتب بالاتر تانژانت، نیاز به محاسبات بیشتر دارد. در مثال بعدی، نحوه انجام این محاسبات را توضیح میدهیم.
مثال ۱۰: محاسبه مشتق مرتبه سوم تانژانت
مشتق مرتبه سوم $$ f ( x ) = \tan ( x ) $$ را به دست بیاورید.
صورت سوال، $$ f ^ { \prime \prime \prime } ( x ) $$ (مشتق مرتبه سوم) را از ما میخواهد. برای به دست آوردن این مشتق، ابتدا مشتقهای مرتبه اول و دوم را تعیین میکنیم. مشتق مرتبه اول تانژانت عبارت است از:
$$
f ^ { \prime } ( x ) = \tan ^ { \prime } ( x ) = \sec ^ ۲ ( x )
$$
اگر از عبارت بالا مشتق بگیریم، مشتق مرتبه دوم تانژانت تعیین میشود. برای این کار، فرمول مشتق ضرب دو تابع را مینویسیم:
$$
\frac { d } { d x } [ u ( x ) v ( x ) ] = u ( x ) v ' ( x ) + v ( x ) u ' ( x )
$$
عبارت $$ \sec ^ ۲ ( x ) $$ را به صورت ضرب دو تابع سکانت بازنویسی میکنیم:
$$ \sec ^ ۲ ( x ) = \sec ( x ) \cdot \sec ( x ) $$
یکی از سکانتها را برابر با u(x) و دیگری را برابر با v(x) در نظر میگیریم:
$$ u ( x ) = \sec ( x ) $$
$$ v ( x ) = \sec ( x ) $$
مشتق u(x) و v(x) (مشتق سکانت) برابر است با:
$$ u ^ { \prime }( x ) = \sec ( x ) \tan ( x ) $$
$$ v ^ { \prime }( x ) = \sec ( x ) \tan ( x ) $$
روابط به دست آمده را درون فرمول مشتق ضرب دو تابع قرار میدهیم:
$$
\frac { d } { d x } [ \sec ( x ) \cdot \sec ( x ) ] = \sec ( x ) \sec ( x ) \tan ( x ) + \sec ( x ) \sec ( x ) \tan ( x )
$$
$$
\frac { d } { d x } \sec ^ ۲( x ) = \sec ^ ۲ ( x ) \tan ( x ) + \sec ^ ۲ ( x ) \tan ( x )
$$
$$
\frac { d } { d x } \sec ^ ۲( x ) = ۲ \tan ( x ) \sec ^ ۲ ( x )
$$
به این ترتیب، برای مشتق مرتبه دوم تانژانت، داریم:
$$
\frac { d ^ ۲ } { d x ^ ۲ } \tan ( x ) = \frac { d } { d x } \sec ^ ۲( x ) = ۲ \tan ( x ) \sec ^ ۲ ( x )
$$
$$
f ^ { \prime \prime } ( x ) = \frac { d ^ ۲ } { d x ^ ۲ } \tan ( x ) = ۲ \tan ( x ) \sec ^ ۲ ( x )
$$
با مشتقگیری از عبارت سمت راست، به مشتق مرتبه سوم تانژانت میرسیم:
$$
f ^ { \prime \prime \prime } ( x ) = \frac { d ^ ۳ } { d x ^ ۳ } \tan ( x ) = \frac { d ^ ۲ } { d x ^ ۲ } \sec ^ ۲ ( x ) =\frac { d } { d x } \left [ ۲ \tan ( x ) \sec ^ ۲ ( x ) \right ]
$$
برای به دست آوردن این مشتق نیز میتوانیم از فرمول مشتق ضرب دو تابع استفاده کنیم. به این منظور، فرمول مذکور را با پارامترهای متفاوت مینویسیم:
$$
\frac { d } { d x } [ g ( x ) h ( x ) ] = g ( x ) h ' ( x ) + h ( x ) g ' ( x )
$$
در عبارت $$ ۲ \tan ( x ) \sec ^ ۲ ( x ) $$، یکی از عبارتها را برابر با g(x) و دیگری را برابر با h(x) در نظر میگیریم:
$$ g ( x ) = ۲ \tan ( x ) $$
$$ h ( x ) = \sec ^ ۲ ( x ) $$
مشتق این توابع عبارت است از:
$$ g ^ { \prime } = ۲ \sec ^ ۲ ( x ) $$
$$ h ^ { \prime } = ۲ \tan ( x ) \sec ^ ۲ ( x ) $$
توابع و مشتقهایشان را درون فرمول مشتق ضرب دو تابع قرار میدهیم:
$$
\frac { d } { d x } [ g ( x ) h ( x ) ] = g ( x ) h ' ( x ) + h ( x ) g ' ( x )
$$
$$
\frac { d } { d x } [ ۲ \tan ( x ) \cdot \sec ^ ۲ ( x ) ] = \left ( ۲ \tan ( x ) \cdot ۲ \tan ( x ) \sec ^ ۲ ( x ) \right ) + \left ( \sec ^ ۲ ( x ) \cdot ۲ \sec ^ ۲ ( x ) \right )
$$
$$
\frac { d } { d x } [ ۲ \tan ( x ) \cdot \sec ^ ۲ ( x ) ] = ۴ \tan ^ ۲ \sec ^ ۲ ( x ) +۲ \sec ^ ۴ ( x )
$$
بر اساس قوانین مثلثات، بین مربع تانژانت و مربع سکانت، رابطه زیر برقرار است:
$$ ۱ + \tan ^ ۲ ( x ) = \sec ^ ۲ ( x ) $$
رابطه بالا را به صورت زیر بازنویسی میکنیم:
$$
\tan ^ ۲ ( x ) = \sec ^ ۲ ( x ) - ۱
$$
به جای مربع تانژانت در جواب مشتق، رابطه بالا را قرار میدهیم:
$$
\frac { d } { d x } [ ۲ \tan ( x ) \cdot \sec ^ ۲ ( x ) ] = ۴ \sec ^ ۲ ( x ) ( \sec ^ ۲ ( x ) - ۱ ) + ۲ \sec ^ ۴ ( x )
$$
$$
\frac { d } { d x } [ ۲ \tan ( x ) \cdot \sec ^ ۲ ( x ) ] = ۴ \sec ^ ۴ ( x ) - ۴ \sec ^ ۲ ( x ) + ۲ \sec ^ ۴ ( x )
$$
$$
\frac { d } { d x } [ ۲ \tan ( x ) \cdot \sec ^ ۲ ( x ) ] = ۶ \sec ^ ۴ ( x ) - ۴ \sec ^ ۲ ( x )
$$
در نتیجه:
$$
f ^ { \prime \prime \prime } ( x ) = \frac { d ^ ۳ } { d x ^ ۳ } \tan ( x ) = ۶ \sec ^ ۴ ( x ) - ۴ \sec ^ ۲ ( x )
$$
به این ترتیب، مشتق مرتبه سوم تانژانت را به دست آوردیم.
رابطه بین مشتق و انتگرال تانژانت
مشتق و انتگرال، دو مفهوم مهم در ریاضیات هستند که برعکس یکدیگر عمل میکنند. هنگام مشتقگیری از یک تابع، بعد آن کاهش مییابد در صورتی که با انتگرالگیری، بعد تابع افزایش مییابد. هدف از به دست آوردن مشتق، تعیین شیب نمودار در یک نقطه مشخص است. در طرف مقابل، انتگرالگیری، به منظور تعیین مساحت زیر منحنی مورد استفاده قرار میگیرد.
انتگرال تانژانت برابر است با:
$$
\int \tan ( x ) dx = \ln | \sec ( x ) | + C
$$
یا
$$
\int \tan ( x ) dx = - \ln | \cos ( x ) | + C
$$
اگر از جواب انتگرال تانژانت ($$ \ln | \sec ( x ) | + C $$ یا $$ - \ln | \cos ( x ) | + $$) مشتق بگیریم، به تابع تانژانت میرسیم. به عبارت دیگر:
$$
\frac { d }{ d x } \left [ \int \tan ( x ) dx \right ] = \frac { d }{ d x } \left [ \ln | \sec ( x ) | + C \right ] = \tan ( x )
$$
$$
\frac { d }{ d x } \left [ \int \tan ( x ) dx \right ] = \frac { d }{ d x } \left [ - \ln | \cos ( x ) | + C \right ] = \tan ( x )
$$
در نتیجه، مشتق انتگرال تانژانت برابر با خود تانژانت است.
مثال ۱۱: محاسبه انتگرال تانژانت
انتگرال $$ e ^ { x } \tan ( e ^ x ) $$ را تعیین کنید.
میخواهیم انتگرال زیر را به دست بیاوریم:
$$
\int \left ( e ^ { x } \tan ( e ^ x ) \right ) dx
$$
برای حل این انتگرال، تغییر متغیر زیر را در نظر میگیریم:
$$ u = e ^ x $$
با مشتقگیری از دو طرف رابطه بالا بر حسب x، به رابطه زیر میرسیم:
$$ \frac { d } { d x } e ^ x = \frac { d } { d x } u $$
مشتق $$ e ^ x $$ با خودش برابر میشود. بنابراین، داریم:
$$ e ^ x = \frac { d u } { d x } $$
رابطه بالا را بر حسب du بازنویسی میکنیم:
$$ d u = e ^ x d x $$
با توجه به این تغییر متغیرها، انتگرال مورد سوال به فرم زیر درمیآید:
$$
\int \left ( e ^ { x } \tan ( e ^ x ) \right ) dx = \int \left ( u \tan ( u ) \right ) d x
$$
به جای udx، میتوانیم معادل آن (du) را جایگذاری کنیم:
$$
\int \left ( e ^ { x } \tan ( e ^ x ) \right ) dx = \int \tan ( u ) d u
$$
انتگرال tan(u) بر حسب u برابر است با:
$$
\int \left ( e ^ { x } \tan ( e ^ x ) \right ) dx = \int \tan ( u ) d u = - \ln | \cos ( u ) | + C
$$
اکنون، به جای u، معادل آن را قرار میدهیم:
$$
\int \left ( e ^ { x } \tan ( e ^ x ) \right ) dx = - \ln | \cos ( e ^ x ) | + C
$$
جدول فرمول های مشتق تانژانت
در بخشهای قبلی، به معرفی فرمولهای مهم برای مشتقگیری از تابع تانژانت و توابع مرتبط با آن پرداختیم. در این بخش، این فرمولها را در قالب یک جدول ارائه میکنیم.
| فرم تابع | مشتق تابع |
| $$ \tan ( x ) $$ | $$ \sec ^ { ۲ } ( x ) $$ |
| $$ a \tan ( x ) $$ | $$ a \sec ^ { ۲ } ( x ) $$ |
| $$ a \tan ( b x ) $$ | $$ a b \sec ^ { ۲ } ( x ) $$ |
| $$ a \tan ( b x + c ) $$ | $$ a b \sec ^ { ۲ } ( x ) $$ |
| $$ \tan ^ n ( x ) $$ | $$ n \sec ^ ۲ ( x ) \tan ^ { n - ۱ } ( x ) $$ |
| $$ \tan ( u ( x ) ) $$ | $$ u ^ { \prime } ( x ) \sec ^ ۲ ( u ( x ) ) $$ |
| $$ a \arctan \left ( b \text { u } ( x ) + c \right) $$ | $$ \frac { a b \text { u } ^ { \prime } ( x ) }{ \left ( b \text { u } ( x ) + c \right ) ^ ۲ + ۱ } $$ |
| $$ a \tanh ( b \text { u } ( x ) + c ) $$ | $$ a b \text { u } ^ { \prime } ( x )\sec ^ ۲ ( b \text { u } (x ) + c ) $$ |
| $$ a \text { arctanh } ( b \text { u } ( x ) + c ) $$ | $$ \frac { a b \text { u } ^ { \prime } ( x ) }{ ۱ - b ^ ۲ \text { u } ^ ۲ ( x ) - ۲ b c \text { u } ( x ) - c ^ ۲} $$ |
| $$ \frac { d ^ ۲ } { d x ^ ۲ } \tan ( x ) $$ | $$ ۲ \tan ( x ) \sec ^ ۲ ( x ) $$ |
| $$ \frac { d ^ ۳ } { d x ^ ۳ } \tan ( x ) $$ | $$ ۶ \sec ^ ۴ ( x ) - ۴ \sec ^ ۲ ( x ) $$ |
حل تمرین مشتق تانژانت
در این بخش، برای آشنایی بیشتر و بهتر با مبحث مشتق tan، به حل چندین تمرین متنوع میپردازیم.
تمرین ۱: محاسبه مشتق ضرب تانژانت
مشتق y را به دست بیاورید.
$$ y = ۶ x ^ ۵ \tan ( x ) $$
y، حاصل ضرب تابع مثلثاتی $$ \tan ( x ) $$ در تابع $$ ۶ x ^ ۵ $$ است. بنابراین، برای به دست آوردن مشتق آن میتوانیم از فرمول مشتق ضرب دو تابع استفاده کنیم. این فرمول به صورت زیر نوشته میشود:
$$
\frac { d } { d x } [ f ( x ) g ( x ) ] = f ( x ) g ' ( x ) + g ( x ) f ' ( x )
$$
بنابراین، قدم اول در تعیین مشتق y، مشخص کردن f(x) و g(x) و مشتق هر یک از آنها است:
$$ f ( x ) = ۶ x ^ ۵ $$
$$ f ^ { \prime } ( x ) = ۵ \times ۶ x ^ { ۵ - ۱ } $$
$$ f ^ { \prime } ( x ) = ۳۰ x ^ { ۴ } $$
$$ g ( x ) = \tan ( x ) $$
$$ g ^ { \prime } ( x ) = \sec ^ ۲ ( x ) $$
به این ترتیب، داریم:
$$ \frac { d } { d x } [ f ( x ) g ( x ) ] = f ( x ) g ' ( x ) + g ( x ) f ' ( x ) $$
$$ \frac { d } { d x } [ ۶ x ^ ۵ \tan ( x ) ] = ۶ x ^ ۵ \sec ^ ۲ ( x ) + \tan ( x ) \cdot ۳۰ x ^ ۴ $$
در نتیجه:
$$ y ^ { \prime } = ۶ x ^ ۵ \sec ^ ۲ ( x ) + ۳۰ x ^ ۴ \tan ( x ) $$
در برخی از موارد (مخصوصا مسائل دارای ضریبهای عددی متعدد)، بهتر است پیش از شروع مشتقگیری، ضرایب ثابت را از معادله خارج کنید. این کار، احتمال خطای محاسباتی را کاهش میدهد. به عنوان مثال، در این تمرین، میتوانستیم با حذف ضریب عددی ۶، f(x) و g(x) را به صورت زیر در نظر بگیریم:
$$ f ( x ) = x ^ ۵ $$
$$ f ^ { \prime } ( x ) = ۵ x ^ { ۴ } $$
$$ g ( x ) = \tan ( x ) $$
$$ g ^ { \prime } ( x ) = \sec ^ ۲ ( x ) $$
به این ترتیب، فرمول مشتق به صورت زیر نوشته میشود:
$$
۶ \left [ \frac { d } { d x } \left ( x ^ ۵ \tan ( x ) \right ) \right ] = ۶ \left ( x ^ ۵ \sec ^ ۲ ( x ) + ۵ x ^ ۴ \tan ( x ) \right )
$$
تمرین ۲: محاسبه مشتق تقسیم تانژانت
مشتق f(x) را تعیین کنید.
$$ f ( x ) = \frac { \tan ^ ۲ ( x ) } { ۴ x ^ ۲ } $$
f'(x)، با استفاده از فرمول مشتق تقسیم دو تابع تعیین میشود. این فرمول عبارت است از:
$$ \frac { d } { d x } \left [ \frac { u ( x ) }{ v ( x ) } \right ] = \frac { v ( x ) u ^ { \prime } ( x ) - u ( x ) v ^ { \prime } ( x ) } { v ^ ۲ ( x ) } $$
صورت سوال، مشتق زیر را از ما میخواهد:
$$ \frac { d } { d x } \left ( \frac { \tan ^ ۲ ( x ) } { ۴ x ^ ۲ } \right ) $$
برای سادگی محاسبات، ثابت $$ \frac { ۱ } { ۴ } $$ را از درون رابطه مشتق بیرون میکشیم:
$$
f ^ { \prime } ( x ) = \frac { ۱ } { ۴ } \times\frac { d } { d x } \left [ \frac { \tan ^ ۲ ( x ) } { x ^ ۲ } \right ]
$$
صورت کسر را برابر با u(x) و مخرج را برابر با v(x) در نظر میگیریم:
$$ u ( x ) = \tan ^ ۲ ( x ) $$
$$ v ( x ) = x ^ ۲ $$
مشتق این توابع عبارت است از:
$$ u ^ { \prime } ( x ) = ۲ \tan ( x ) \sec ^ ۲ ( x ) $$
$$ v ^ { \prime } ( x ) = ۲ x $$
توابع u(x) و v(x) را به همراه مشتقهایشان درون فرمول مشتق تقسیم دو تابع قرار میدهیم:
$$
\frac { d } { d x } \left [ \frac { u ( x ) }{ v ( x ) } \right ] = \frac { v ( x ) u ^ { \prime } ( x ) - u ( x ) v ^ { \prime } ( x ) } { v ^ ۲ ( x ) }
$$
$$
\frac { d } { d x } \left [ \frac { \tan ^ ۲ ( x ) }{ x ^ ۲ } \right ] = \frac {x ^ ۲
\cdot ۲ \tan ( x ) \sec ^ ۲ ( x ) - \tan ^ ۲ ( x ) \cdot ۲ x } { \left ( x ^ ۲ \right ) ^ ۲ }
$$
$$
\frac { d } { d x } \left [ \frac { \tan ^ ۲ ( x ) }{ x ^ ۲ } \right ] = \frac { ۲ x ^ ۲ \tan ( x ) \sec ^ ۲ ( x ) - ۲ x \tan ^ ۲ ( x )} { x ^ ۴}
$$
از $$ ۲ x \tan ( x ) $$ در صورت سوال فاکتور میگیریم:
$$
\frac { d } { d x } \left [ \frac { \tan ^ ۲ ( x ) }{ x ^ ۲ } \right ] = \frac { ۲ x \tan ( x ) \left [ x \sec ^ ۲ ( x ) - \tan ( x ) \right ] } { x ^ ۴ }
$$
$$
\frac { d } { d x } \left [ \frac { \tan ^ ۲ ( x ) }{ x ^ ۲ } \right ] = \frac { ۲ \tan ( x ) \left [ x \sec ^ ۲ ( x ) - \tan ( x ) \right ] } { x ^ ۳ }
$$
جواب مشتق بالا را در رابطه زیر جایگذاری میکنیم:
$$
f ^ { \prime } ( x ) = \frac { ۱ } { ۴ } \times\frac { d } { d x } \left [ \frac { \tan ^ ۲ ( x ) } { x ^ ۲ } \right ]
$$
$$
f ^ { \prime } ( x ) = \frac { ۱ } { ۴ } \times \frac { ۲ \tan ( x ) \left [ x \sec ^ ۲ ( x ) - \tan ( x ) \right ] } { x ^ ۳ }
$$
$$
f ^ { \prime } ( x ) = \frac { \tan ( x ) \left [ x \sec ^ ۲ ( x ) - \tan ( x ) \right ] } { ۲ x ^ ۳ }
$$
تمرین ۳: محاسبه مشتق تانژانت کتانژانت
مشتق $$ \tan ( \cot ( x ) ) $$ را به دست بیاورید.
$$ \tan ( \cot ( x ) ) $$، یک تابع تو در تو است که میتوان آن را به صورت $$ \tan ( u ( x ) ) $$ نوشت. فرمول مشتق $$ \tan ( u ) $$ به صورت زیر نوشته میشود:
$$ \frac { d } { d x } \tan ( u ( x ) ) = u ^ { \prime } ( x ) \sec ^ ۲ ( u ) $$
با توجه به این فرمول، برای حل مشتق مورد سوال، باید $$ \cot ( x ) $$ را برابر با u در نظر بگیریم:
$$ u ( x )= \cot ( x ) $$
به این ترتیب، داریم:
$$ u ^ { \prime } ( x ) = - \csc ^ ۲ ( x ) $$
با قرار دادن u(x) و u'(x) در فرمول مشتق $$ \tan ( u ) $$، به جواب سوال میرسیم:
$$ \frac { d } { d x } \tan ( u ( x ) ) = u ^ { \prime } ( x ) \sec ^ ۲ ( u ) $$
$$ \frac { d } { d x } \tan ( u ( x ) ) = - \csc ^ ۲ ( x ) \sec ^ ۲ ( \cot ( x ) ) $$
تمرین ۴: اثبات رابطه مثلثاتی با استفاده از مشتق tan
ثابت کنید اگر $$ y = \csc ( x ) + x \tan ( x ) $$ باشد، $$ y ^ { \prime } = - \csc ( x ) \cot ( x ) + \tan ( x ) + x + x \tan ^ ۲ ( x ) sec ^ ۲ ( x ) $$ خواهد بود.
برای حل این تمرین، از فرمول مشتق جمع، ضرب و تقسیم توابع استفاده میکنیم. برای شروع، y را در نظر بگیرید:
$$ y = \csc ( x ) + x \tan ( x ) $$
بر اساس قوانین مشتقگیری، مشتق جمع دو تابع برابر با مجموع مشتق دو تابع است. به عبارت دیگر:
$$
y ^ { \prime } = \frac { d } { d x } ( \csc ( x ) + x \tan ( x ) ) = \frac { d } { d x } \csc ( x ) + \frac { d } { d x }( x \tan ( x ) )
$$
بنابراین، ابتدا باید از هر یک از توابع موجود در تابع y، مشتق بگیریم. برای مشتق تابع اول داریم:
$$ \frac { d } { d x } \csc ( x ) = - \cot ( x ) \csc ( x ) $$
در ادامه نحوه اثبات این مشتق را توضیح میدهیم. تابع کسکانت، عکس تابع سینوس است:
$$ \csc ( x ) = \frac { ۱ } { \sin ( x ) } $$
بنابراین، مشتق کسکانت از طریق فرمول مشتق تقسیم دو تابع به دست میآید. این فرمول، به صورت زیر نوشته میشود:
$$ \frac { d } { d x } \left ( \frac { ۱ } { \sin ( x ) } \right ) $$
$$
\frac { d } { d x } \left ( \frac { ۱ } { \sin ( x ) } \right ) = \frac { \sin ( x ) \times \frac { d } {d x } ( ۱ ) - ۱ \times \sin ^ { \prime } ( x ) }{ ( \sin ( x ) ) ^ ۲}
$$
میدانیم مشتق سینوس برابر با کسینوس بوده و مشتق یک عدد ثابت (مانند ۱) برابر با ۰ است. بنابراین:
$$
\frac { d } { d x } \left ( \frac { ۱ } { \sin ( x ) } \right ) = \frac { \sin ( x ) \times ۰ - \cos ( x ) }{ \sin ^ ۲ ( x ) }
$$
$$
\frac { d } { d x } \left ( \frac { ۱ } { \sin ( x ) } \right ) = - \frac { \cos ( x ) }{ \sin ^ ۲ ( x ) }
$$
جواب مشتق بالا را به صورت زیر بازنویسی میکنیم:
$$
\frac { d } { d x } \left ( \frac { ۱ } { \sin ( x ) } \right ) = - \frac { \cos ( x ) }{ \sin ( x ) } \times \frac { ۱ }{ \sin ( x ) }
$$
نسبت کسینوس به سینوس با کتانژانت و نسبت ۱ بر روی سینوس با کسکانت برابر است. به این ترتیب:
$$
\frac { d } { d x } \left ( \frac { ۱ } { \sin ( x ) } \right ) = - \cot ( x ) \csc ( x )
$$
$$
\frac { d } { d x } \csc ( x ) = - \cot ( x ) \csc ( x )
$$
اکنون به سراغ عبارت دوم، یعنی $$ x \tan ( x ) $$ میرویم. مشتق این عبارت به کمک فرمول مشتق ضرب دو تابع تعیین میشود. بر اساس این فرمول، داریم:
$$
\frac { d } { d x }( x \tan ( x ) )
$$
$$
\frac { d } { d x }( x \tan ( x ) ) = x ^ { \prime } \tan ( x ) + x \tan ^ { \prime } ( x )
$$
$$
\frac { d } { d x }( x \tan ( x ) ) = ۱ \times \tan ( x ) + x \sec ^ ۲ ( x )
$$
$$
\frac { d } { d x }( x \tan ( x ) ) = \tan ( x ) + x \sec ^ ۲ ( x )
$$
مشتقهای به دست آمده را در فرمول مشتق جمع دو تابع قرار میدهیم:
$$
y ^ { \prime } = \frac { d } { d x } ( \csc ( x ) + x \tan ( x ) ) = \frac { d } { d x } \csc ( x ) + \frac { d } { d x }( x \tan ( x ) )
$$
$$
y ^ { \prime } = \frac { d } { d x } ( \csc ( x ) + x \tan ( x ) ) = - \cot ( x ) \csc ( x ) + \tan ( x ) + x \sec ^ ۲ ( x )
$$
با توجه به رابطه بین مربع سکانت و تانژانت، به رابطه زیر میرسیم:
$$
y ^ { \prime } = - \cot ( x ) \csc ( x ) + \tan ( x ) + x ( ۱ + \tan ^ ۲ ( x ) )
$$
$$
y ^ { \prime } = - \cot ( x ) \csc ( x ) + \tan ( x ) + x + x\tan ^ ۲ ( x )
$$
تمرین ۵: محاسبه سرعت ذره با استفاده از مشتق تانژانت وارون
معادله مکان یک ذره در زمان t (به شرط $$ t \ge \frac { ۱ } { ۲ } $$) عبارت است از:
$$ s ( t ) = \tan ^ { - ۱ } ( \frac { ۱ } { t } ) $$
سرعت ذره در زمان $$ t = ۱ $$ را محاسبه کنید.
اگر از معادله مکان یک ذره بر حسب زمان مشتق بگیریم، به معادله سرعت یا تندی آن ذره میرسیم. به عبارت دیگر، شیب نمودار مکان-زمان برابر با سرعت است. بنابراین، جواب سوال، با مشتقگیری از s(t) بر حسب پارامتر t به دست میآید. s(t)، یک تابع مثلثاتی وارون و تو در تو است. فرم کلی این تابع به صورت زیر نوشته میشود:
$$ s ( t ) = \tan ^ { - ۱ } ( \text { u } ( t ) ) $$
مشتق تابع بالا برابر است با:
$$ \frac { d } { d t } \tan ^ { - ۱ } ( \text { u } ( t ) ) = \frac { \text { u } ^ { \prime } ( t ) } { \text { u } ^ ۲ ( t ) + ۱ } $$
با توجه به صورت سوال، $$ \frac { ۱ } { t } $$ را برابر با (t)u قرار میدهیم. به این ترتیب، داریم:
$$ u ( t ) = \frac { ۱ } { t } $$
$$ u ^ { \prime } ( t ) = - \frac { ۱ } { t ^ ۲ } $$
این روابط را درون فرمول مشتق تانژانت وارون u جایگذاری میکنیم:
$$
\frac { d } { d x } \tan ^ { - ۱ } ( \frac { ۱ } { t } ) = \frac { - \frac { ۱ } { t ^ ۲ } } { \left ( \frac { ۱ } { t } \right )^ ۲ + ۱ }
$$
$$
\frac { d } { d x } \tan ^ { - ۱ } ( \frac { ۱ } { t } ) = \frac { - \frac { ۱ } { t ^ ۲ } } { \frac { ۱ } { t ^ ۲ } + ۱ }
$$
$$
\frac { d } { d x } \tan ^ { - ۱ } ( \frac { ۱ } { t } ) = - \frac { \frac { ۱ } { t ^ ۲ } } { \frac { ۱ + t ^ ۲ } { t ^ ۲ } }
$$
$$
\frac { d } { d x } \tan ^ { - ۱ } ( \frac { ۱ } { t } ) = - \frac { ۱ } { ۱ + t ^ ۲ }
$$
بنابراین:
$$
s ^ { \prime } ( t ) = - \frac { ۱ } { ۱ + t ^ ۲ }
$$
صورت سوال، سرعت ذره در زمان $$ t = ۱ $$ را از ما میخواهد. برای به دست آوردن این سرعت، عدد ۱ را درون رابطه بالا قرار میدهیم:
$$
s ^ { \prime } ( ۱ ) = - \frac { ۱ } { ۱ + ۱ ^ ۲ }
$$
$$
s ^ { \prime } ( ۱ ) = - \frac { ۱ } { ۲ }
$$
از اینرو:
$$
v ( ۱ ) = - \frac { ۱ } { ۲ }
$$
در نتیجه، سرعت ذره در زمان t=۱ برابر با منفی یکدوم است.
سوالات متداول در رابطه با مشتق تانژانت
در این بخش، به برخی از پرتکرارترین سوالات در رابطه با مبحث مشتق tan به طور مختصر پاسخ میدهیم.
تعریف مشتق tan چیست ؟
مشتق تابع مثلثاتی تانژانت، به صورت شیب خط مماس بر نمودار این تابع در یک نقطه مشخص تعریف میشود.
مشتق tan برابر با چیست ؟
مشتق تانژانت برابر با مربع سکانت است.
فرمول مشتق tan چیست ؟
فرمول مشتق تانژانت به صورت tan'(x)=sec^۲(x) نوشته میشود.
مشتق تانژانت هیپربولیک چیست ؟
مشتق تانژانت هیپربولیک برابر با مربع سکانت هیپربولیک است.
فرمول مشتق tanh چیست ؟
فرمول مشتق تانژانت هیپربولیک به صورت tanh'(x)=sech^۲(x) نوشته میشود.
مشتق مرتبه دوم tan چیست ؟
مشتق مرتبه دوم تانژانت برابر با دو تانژانت در مربع سکانت است.
مشتق نسبت عکس tan چیست ؟
مشتق نسبت عکس تانژانت، برابر با منفی مربع کسکانت (مشتق کتانژانت) است.
مشتق انتگرال tan چیست ؟
مشتق انتگرال tan برابر با tan است.
رابطه بین مشتق tan و cot چیست ؟
مشتق تانژانت برابر با مربع سکانت و مشتق کتانژانت برابر با منفی مربع کسکانت است. اگر مشتق tan را بر مشتق cot تقسیم کنیم، به منفی مربع تانژانت میرسیم.










