انتگرال و محاسبات آن — به زبان ساده

در این مطلب از مجله فرادرس با مفهوم انتگرال و محاسبات آن به زبان ساده آشنا میشویم. از مهمترین ابزارهای ریاضیاتی تاریخ علم، که بشر تاکنون به آن دست یافته، «انتگرال» (Integral) است. از این مفهوم میتوان بهمنظور محاسبه مساحت، حجم و طول استفاده کرد. نماد استفاده شده برای توصیف انتگرال، s کشیده است. این حرف مخفف کلمه لاتین «Sum» به معنای جمع است. برای شروع، با استفاده از مساحت سطح زیر نمودار، به معرفی این مفهوم میپردازیم. بهمنظور درک مفهوم انتگرال در ابتدا بایستی با مشتق آشنایی داشته باشید. در ادامه مفاهیمی مرتبط با انتگرال همچون انتگرال سطحی، انتگرال دوگانه و انتگرال توابع مثلثاتی را توضیح خواهیم داد.
سوال:
مساحت سطح زیر نمودار تابع (y=f(x چقدر است؟
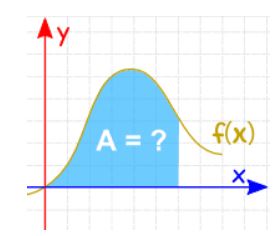
تقسیمبندی مساحت
همانطور که در شکل زیر نیز میبینید، بهمنظور محاسبه مساحت سطحِ زیر یک نمودار میتوان آن را چند قسمت کرد. برای راحتی کار عرض تمامی این بخشها، یکسان و برابر با $$\Delta x$$ در نظر گرفته میشود.
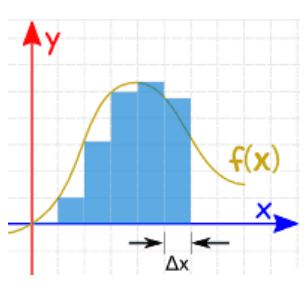
بنابراین همانگونه که در بالا بیان شد، با محاسبه مستطیلهای فرض شده، میتوان مساحت زیر نمودار را بدست آورد. احتمالا شما نیز متوجه شدهاید که مساحت محاسبه شده با مقدار مدنظر تفاوت خواهد داشت. همانطور که در شکل زیر نیز میبینید، نواحی قرمز رنگ، اختلاف مساحت مدنظر و مساحت محاسبه شده را نشان میدهند. به نظر شما چطور میتوان مقدار بدست آمده را به مقدار واقعی نزدیکتر کرد؟
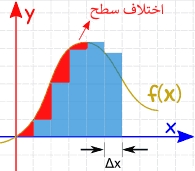
حال با همان روش قبلی، سطوح را تقسیمبندی کنید، اما این بار فواصل $$\Delta x$$ را کوچکتر در نظر بگیرید. در شکل زیر نیز مشخص است که با کوچک کردن این فواصل، مساحت محاسبه شده و مساحت مدنظر به یکدیگر نزدیکتر شدهاند.
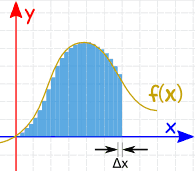
بر همین مبنا، مطابق شکل زیر اگر $$\Delta x$$ به صفر میل کند، (مساحت به بینهایت بخش تقسیم شود) مساحت مد نظر ما نیز بدست میآید.
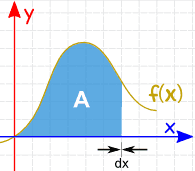
محاسبه مساحت
به نظر میرسد با محاسبه مساحت بینهایت مستطیل، میتوان سطح زیر یک نمودار را بدست آورد. اما سوال اینجا است که به راستی چگونه میتوان بینهایت عدد را محاسبه کرد؟ واقعیت این است که نیازی نیست تمامی این مساحتها را بدانیم، چراکه نیوتن راه کوتاهتری را به ما نشان داده. او اثبات کرده که انتگرال و مشتق عکس هم هستند. برای درک بهتر به مثالهای زیر توجه فرمایید.
توجه داشته باشید که به منظور حل یک انتگرال میتوان از تکنیکهای مختلفی استفاده کرد. در مطالب پیشین مجله فرادرس در مورد مهمترین تکنیکهای حل انتگرال صحبت کردیم. معروفترینِ این روشها، جزء به جزء، تغییر متغیر، روشهای عددی و تجزیه کسر (کسرهای جزئی) هستند؛ البته در این لینک به کلیات روشهای حل نیز اشاره شده است.
مثال ۱
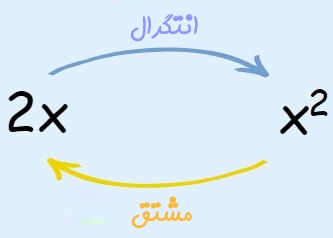
انتگرال تابع y=2x را بیابید.
میدانیم که مشتق تابع $$x^2$$ برابر با ۲x است. بنابراین انتگرال 2x برابر با x2 میشود.
در بخش دوم در مورد قوانین حاکم در حل انتگرال یک تابع، بیشتر بحث خواهیم کرد. توجه داشته باشید که مساحت را میتوان با استفاده از انتگرال دوگانه نیز بدست آورد.
نماد انتگرال
همانطور که در بالا نیز بیان شد، نماد استفاده شده به منظور توصیف انتگرال، حرف s کشیده است. پس از این نماد، تابعی قرار میگیرد که هدف ما محاسبه انتگرال آن است. سپس dx قرار میگیرد که نشان دهنده عرض هرکدام از مستطیلها است.

در حالت کلی قالب نوشتن یک معادله انتگرالی به شکل زیر است.
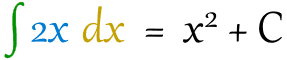
C به چه معنا است؟
در مثال شماره ۱، پاسخ را برابر با $$x^2$$ بدست آوردیم، اما چرا در جواب نهایی، آن را با C جمع کردیم؟ عدد C ثابت انتگرال است. دلیل قرار گرفتن C این است که اگر تابع $$x^2$$ را با هر عدد ثابتی جمع کنیم و سپس از آن مشتق بگیریم، همچنان 2x ظاهر میشود. در حقیقت مشتق توابع $$ x^2+9 ,x^2+1025,x^2+4 $$ همگی برابر با ۲x هستند، در نتیجه تمامی آنها را میتوان به عنوان پاسخ انتگرال مثال ۱ در نظر گرفت.
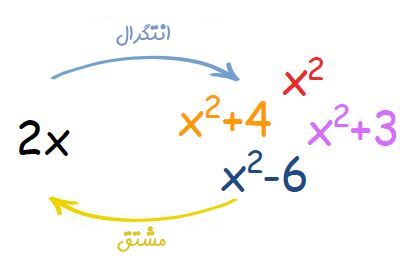
از این رو بهمنظور بیان این اعداد از ثابت C استفاده میکنیم.
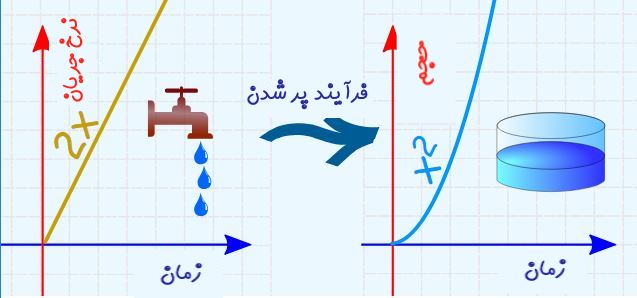
مخزن آب
انتگرالگیری را میتوان مشابه با مخزن آبی دانست که توسط یک شیر در حال پر شدن است. تابع ورودی، همان نرخ جریان آب در هر لحظه است. با انتگرالگیری از این نرخ (جمع زدن مقادیر آب اضافه شده در هر لحظه)، میتوان حجم آب موجود درون مخزن را یافت.
اگر نرخ جریان ورودی مطابق با تابع 2t تغییر کند، حجم کلی آب موجود در مخزن، در زمان t برابر با $$t^2$$ است. [ با فرض اینکه در حالت اولیه مخزن خالی بوده باشد.]
مثال ۲
مخزنی را در نظر بگیرید که جریان آب با نرخ $$2t \space {liter \over s}$$ به آن ریخته میشود. با فرض اینکه مخزن در حالت اولیه خالی بوده باشد، حجم آب موجود در مخزن پس از گذشت زمان ۳ و ۴ ثانیه چقدر است؟
پس از گذشت زمان ۳ ثانیه، نرخ جریان ورودی به مخزن برابر است با:
$$\large 2t = 2×3 = 6 \enspace {liter \over s}$$
همچنین برای محاسبه حجم آب ریخته شده به مخزن، میتوان از تابع 2t، به شکل زیر انتگرال گرفت.
$$\large = \int 2t dt=t^2 = 3^2 = 9 $$
در نتیجه حجم آب موجود در مخزن، در لحظه ۳ ثانیه برابر با ۹ لیتر است. به همین شکل در لحظه t=4 نیز حجم آب وارد شده به مخزن، برابر با لیتر $$۴^2=16$$ خواهد بود.
همین فرآیند را میتوان برعکس نیز انجام داد. یعنی با داشتن مقدار آب درون مخزن، در هر لحظه، نرخ جریان ورودی به آن را در همان لحظه بدست آورد. برای مثال فرض کنید در یک لحظه مشخص میزان آب درون مخزن برابر با ۱۶ لیتر باشد. از آنجایی که حجم آب درون مخزن با استفاده از رابطه $$V=t^2$$ محاسبه میشود، میتوان گفت:
$$\large V=t^2=16 \rightarrow t= \sqrt {16} = 4 \enspace s$$
$$\large \rightarrow \enspace \enspace 2t=2×4=8 \enspace {lit \over s}$$
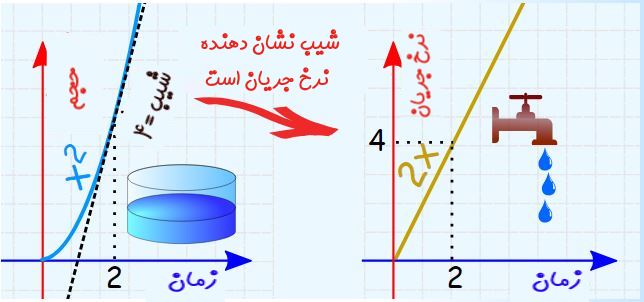
در حقیقت دو بیان زیر معادل هم هستند.
انتگرال نرخ جریان ورودی، حجم آب موجود در مخزن را محاسبه میکند ≡ شیب حجم آب موجود در مخزن، نرخ جریان ورودی به آن را نشان میدهد.
انتگرال دیگر توابع
در بالا به اندازه کافی در مورد تابع 2x صحبت کردیم. در این قسمت قصد داریم تا در مورد نحوه انتگرالگیریِ دیگر توابع بحث کنیم.
مثال ۳
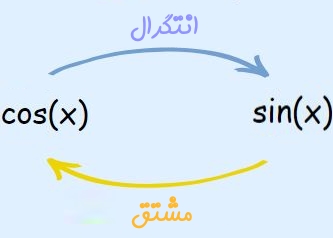
انتگرال تابع $$f(x)=cos(x)$$ را بیابید.
همانطور که میدانید برای محاسبه انتگرال این تابع، بایستی به دنبال رابطهای بگردیم که مشتق آن برابر با (cos (x شود. احتمالا میدانید که تابع مدنظر (sin (x است، چراکه مشتق آن برابر با (cos (x میشود. بنابراین میتوان گفت:
$$\large \int cos (x) dx= sin(x)+C$$
مثال ۴
به نظر شما انتگرال تابعی که به شکل $$f(x)=x^n$$ باشد، به چه صورت است.
برای محاسبه چنین انتگرالی بایستی فکر کنید که مشتق چه تابعی برابر با $$f(x)=x^n$$ میشود. تابعی به شکل زیر را در نظر بگیرید:
$$\large {{x^{n+1} \over {n+1}} +C}$$
مشتق این تابع برابر با $$f'(x)=x^n$$ است. بنابراین میتوان گفت:
$$\large \int \enspace x^n dx = {x^{n+1} \over {n+1}}$$
مثال ۵
حاصل $$ \int x^3 dx $$ را بیابید.
با جایگذاری ۳ بهجای n در معادله بالا داریم:
$$\large \rightarrow \int x^3 dx={x^4 \over 4} + C $$
انتگرال معین و نامعین
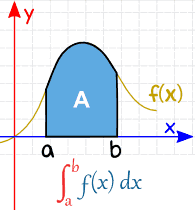
تاکنون انتگرالهایی که محاسبه شد، همگی نامعین بودند. انتگرال معین اصطلاحی است که به منظور محاسبه انتگرال در بازهای مشخص استفاده میشود.
در حقیقت انتگرال معین، مساحت زیر منحنی در بازه مفروض را (مثلا a تا b) محاسبه میکند. شکل زیر مفهوم انتگرال معین را نشان داده است.
در بخش آینده، روشهایی را ارائه خواهیم داد (مانند روش تجزیه کسر) که با استفاده از آنها قادر خواهید بود تا انتگرال توابع مختلف را محاسبه کنید. در آینده انتگرال دوگانه و نحوه محاسبه طول قوس منحنی به کمک انتگرال را نیز توضیح خواهیم داد. همچنین در صورت علاقهمندی میتوانید نحوه بدست آوردن انتگرال توابع مثلثاتی را نیز مطالعه فرمایید.
قبل از شروع آزمون، چند نکته مهم در رابطه با ویژگیهای انتگرال را با یکدیگر مرور میکنیم:
- $$\int_{a}^{b} f( x ) d x = - \ \int_{b}^{a} f( x ) d x$$
- $$\int_{a}^{a} f( x ) d x = 0$$
- $$\int_{a}^{b} c f( x ) d x = c\int_{a}^{b} f( x ) d x $$
- $$\int_{a}^{b} f( x ) \pm g ( x ) d x = \int_{a}^{b} f( x ) d x \pm \int_{a}^{b} g( x ) d x $$
- $$\int_{a}^{b} f( x ) d x = \int_{a}^{c} f( x ) d x + \int_{c}^{b} f( x ) d x$$
آزمون انتگرال و محاسبات آن
در این قسمت به منظور درک بهتر مفهوم انتگرال و محاسبات آن، تعدادی پرسش چهار گزینهای به صورت آزمون تهیه شده است.
اگر مقدار انتگرالهای $$\int_{ 12 }^{ - 10 }f ( x ) d x = 6$$ و $$\int_{ 100 }^{ - 10 }f ( x ) d x = -2 $$ و $$\int_{ 100 }^{ -5 }f ( x ) d x = 4$$ را داشته باشیم، مقدار انتگرال $$\int_{ -5 }^{ 12 }f ( x ) d x $$ برابر است با:
۱۲-
۱۲+
۸+
۸-
برای حل این مسئله از رابطه انتگرالی زیر استفاده میکنیم:
$$\int_{a}^{b} f( x ) d x = \int_{a}^{c} f( x ) d x + \int_{c}^{b} f ( x ) dx $$
۵- یکی از حدهای انتگرال $$\int_{ 100 }^{ -5 }f ( x ) d x = 4$$ است. از آنجا که ۵- حد پایین انتگرال ذکر شده نیست، میتوانیم آن را به صورت زیر به حد پایین انتگرال منتقل کنیم:
$$\int_{ 100 }^{ -5 }f ( x ) d x = 4 \\ \int_{ -5 }^{ 100 }f ( x ) d x = -4 $$
با توجه به رابطه $$$$\int_{a}^{b} f( x ) d x = \int_{a}^{c} f( x ) d x + \int_{c}^{b} f ( x ) dx $$$$، انتگرال $$\int_{ -5 }^{ 12 }f ( x ) d x $$ را میتوانیم به صورت زیر بشکنیم و مقدارهای داده شده را جایگزین کنیم:
$$\int_{ -5 }^{ 12 }f ( x ) d x = \int_{ -5 }^{ 100 }f ( x ) d x + \int_{ 100 }^{ -10 }f ( x ) d x + \int_{ -10 }^{ 12 }f ( x ) d x \\ \int_{ -5 }^{ 12 }f ( x ) d x = - \int_{ 100 }^{ -5 }f ( x ) d x + \int_{ 100 }^{ -10 }f ( x ) d x - \int_{ 12 }^{ -10 }f ( x ) d x = -4 -2 - 6 = -12$$
با توجه به مقدارهای دو انتگرال $$\int_{ 6 }^{ -10 }f ( x ) d x = 23 $$ و $$\int_{ -10 }^{ 6 } g ( x ) d x = -9 $$، حاصل عبارت $$\int_{ -10 }^{ 6 } ( 2 f ( x) - 10 g ( x ) ) dx $$ برابر است با:
۱۳۶
۴۴
۴۴-
۱۴۶-
برای حل این مسئله از دو ویژگی زیر برای انتگرالها استفاده میکنیم:
- $$\int_{ a }^{ b } f( x) dx = - \int_{ b }^{ a } f( x) dx $$
- $$\int_{ a }^{ b } (f( x) \pm g( x) ) dx = \int_{a}^{b} f( x) dx \pm \int_{a}^{b} g( x ) d x $$
با توجه به ویژگی ۲، انتگرال $$\int_{ -10 }^{ 6 } ( 2 f ( x) - 10 g ( x ) ) dx $$ را میتوانیم به صورت زیر بنویسیم:
$$\int_{ -10 }^{ 6 } ( 2 f ( x) - 10 g ( x ) ) dx = \int_{ -10 }^{ 6 } 2 f( x) d x - \int_{ -10 }^{ 6 } 10 g ( x) dx$$
با توجه به آنکه عدد ثابت میتواند بدون تغییر از انتگرال خارج شود، عبارت فوق را میتوانیم به صورت زیر بنویسیم:
$$\int_{ -10 }^{ 6 } ( 2 f ( x) - 10 g ( x ) ) dx = \int_{ -10 }^{ 6 } 2 f( x) d x - \int_{ -10 }^{ 6 } 10 g ( x) dx \\ = 2 \int_{ -10 }^{ 6 } f( x) d x - 10 \int_{ -10 }^{ 6 } g ( x) dx$$
با توجه به آنکه حد پایین انتگرال در عبارت فوق برابر ۱۰- و حد بالا برابر ۶ است، انتگرال $$\int_{ 6 }^{ -10 }f ( x ) d x = 23 $$ را به صورت زیر مینویسیم:
$$ \int_{ -10 }^{ 6 }f ( x ) d x = -23 $$
در نتیجه، مقدار انتگرال $$\int_{ -10 }^{ 6 } ( 2 f ( x) - 10 g ( x ) ) dx $$ برابر است با:
$$\int_{ -10 }^{ 6 } ( 2 f ( x) - 10 g ( x ) ) dx = \int_{ -10 }^{ 6 } 2 f( x) d x - \int_{ -10 }^{ 6 } 10 g ( x) dx \\ = 2 \int_{ -10 }^{ 6 } f( x) d x - 10 \int_{ -10 }^{ 6 } g ( x) dx \\ 2 (-\int_{ 6 }^{ -10 } f( x) d x) - 10 \int_{ -10 }^{ 6 } g ( x) dx \\ = 2(-23)-10 (-9) =44 $$
مقدار انتگرال $$\int_{ 4 }^{ 0 } \sqrt { t } ( t -2 ) dt $$ برابر است با:
$$- \ \frac { 32 } { 15 }$$
$$- \ \frac { 15 } { 32 }$$
$$- \ \frac { 32 } { 12 }$$
$$- \ \frac { 36 } { 15 }$$
ابتدا $$\sqrt { t } $$ را به صورت $$ t ^ { \frac{ 1 } { 2 } $$ مینویسیم و در عبارت $$( t - 2 } $$ ضرب میکنیم:
$$ \sqrt { t } ( t -2 ) = t ^ { \frac { 1 } { 2 } } ( t - 2 ) = t ^ { \frac { 3} { 2 } } - 2 t ^ { \frac { 1 } { 2 } }$$
بنابراین، انتگرال $$\int_{ 4 }^{ 0 } \sqrt { t } ( t -2 ) dt $$ را میتوانیم به صورت زیر حل کنیم:
$$\int_{ 4 }^{ 0 } \sqrt { t } ( t -2 ) dt = \int_{ 4 }^{ 0 } ( t ^ {\frac { 3 } { 2 } } - 2 t ^ { \frac { 3 } { 2 } }) d t \\ = ( \frac { 2 } { 3 } t ^ { \frac { 5 } { 2 } } - \frac { 4 } { 3 } t ^ {\frac { 3 } { 2 }})|_ { 4} ^ { 0 } \\ 0 - ( \frac { 2 } { 3 } (4) ^ { \frac { 5 } { 2 } } - \frac { 4 } { 3 } ( 4 ) ^ {\frac { 3 } { 2 }}) = - \ \frac { 32 } { 15 } $$
مقدار انتگرال $$\int_{ 0 }^{ \frac { \pi } { 3 } } (2 sin \theta - 5 cos \theta) d \theta$$ برابر است با:
$$1 + \frac {5 \sqrt { 3 } } { 2 } $$
$$2 - \frac {5 \sqrt { 3 } } { 2 } $$
$$1 - \frac {5 \sqrt { 3 } } { 2 } $$
$$1 - \frac { \sqrt { 3 } } { 2 } $$
به هنگام حل انتگرال داده شده باید به علامتها بسیار دقت داشته باشیم:
$$\int_{ 0 }^{ \frac { \pi } { 3 } } (2 sin \theta - 5 cos \theta) d \theta= \int_{ 0 }^{ \frac { \pi } { 3 } } 2 sin \theta d \theta - \int_{ 0 }^{ \frac { \pi } { 3 } } 5 cos \theta d \theta \\ = 2 \int_{ 0 }^{ \frac { \pi } { 3 } } sin \theta d \theta - 5 \int_{ 0 }^{ \frac { \pi } { 3 } } cos \theta d \theta \\ = ( - 2 cos \theta - 5 sin \theta )|_ { 0 } ^ { \frac { \pi } { 3 } } \\ = -2 cos (\frac { \pi } { 3 } ) - 5 sin (\frac { \pi} { 3 } ) - ( -2cos ( 0) - 5 sin ( 0 ) ) = -1 -\frac { 5 \sqrt { 3 } } { 2 } + 2 \\ = 1 - \frac {5 \sqrt { 3 } } { 2 }$$
اگر $$\int \frac { x - 1 } { x ^ 3 } \ dx = \frac { 1 } { 2 x ^ 2 } f ( x) + C$$ باشد، آنگاه $$f ( x ) $$ برابر است با:
$$ - 2 x + 1 $$
$$- x + 2 $$
$$ x - 2 $$
$$ 2 x - 1 $$
برای یافتن $$f ( x) $$ باید انتگرال داده شده را حل کنیم:
$$\int \frac { x - 1 } { x ^ 3 } \ dx = \int ({ \frac { x } { x ^ 3 } - \frac { 1 } { x ^ 3 } }) \ dx = \int \frac { 1 } { x ^ 2 } dx - \int \frac { 1 } { x ^ 3 } dx \\ = \int x ^ { -2 } dx - \int x ^ { - 3 } dx \\ = - x ^ { - 1 } + \frac { 1 } { 2 } x ^ { - 2 } + C \\ = - \frac { 1 } { x } + \frac { 1 } { 2 x ^ 2 } + C = \frac { -2 x + 1 } { 2 x ^ 2 } + C \\ = \frac { 1 } { 2 x ^ 2 } ( f (x )) + C \Rightarrow f (X ) = - 2 x +1 $$
اگر $$f ( x ) = x - | x - 2 | $$ باشد، حاصل $$\int_{ 0 }^{ 4 } f ( x ) dx $$ کدام است؟
۲
۳
۴
۵
همانطور که در صورت مسئله مشاهده میکنید، تابع $$ f ( x ) $$ تابع قدر مطلق است. بنابراین، برای محاسبه انتگرال این تابع، ابتدا باید ریشه داخل قدر مطلق را بهدست آوریم و آن را تعیین علامت کنیم. تابع داخل قدر مطلق برابر $$x - 2 $$ است. برای تعیین ریشه، عبارت $$ x - 2 $$ را برابر صفر قرار میدهیم.
$$x - 2 = 0 \\ x = 2 $$
پس از بهدست آوردن ریشه، عبارت $$x - 2 $$ به صورت زیر تعیین علامت میشود:
$$ \begin{cases} | x -2 | = + ( x -2 ) & x > 2 \\ | x - 2 | = - ( x - 2 ) & x < 2\end{cases}$$
اکنون برای حل انتگرال این تابع، باید فاصله ۰ تا ۴ محدوده انتگرالگیری را به دو فاصله صفر تا ۲ و ۲ تا ۴ بشکنیم. در نتیجه، $$\int_{ 0 }^{ 4 } f ( x ) dx $$ به صورت زیر نوشته میشود:
$$\int_{ 0 }^{ 4 } f ( x ) dx = $$\int_{ 0 }^{ 2 } ( x - | x - 2 | ) dx + \int_{ 2 }^{ 4 } ( x - | x - 2 | ) dx $$
تابع $$ x - | x - 2 | $$ در فاصله صفر تا دو، برابر $$x - ( - ( x -2 )) = 2x -2 $$ و در فاصله دو تا چهار، برابر $$x -x + 2 = 2 $$ است. بنابراین، حاصل انتگرال فوق برابر است با:
$$\int_{ 0 }^{ 4 } f ( x ) dx = $$\int_{ 0 }^{ 2 } ( x - | x - 2 | ) dx + \int_{ 2 }^{ 4 } ( x - | x - 2 | ) dx \\ = \int_{ 0 }^{ 2 } ( 2 x - 2 ) dx + \int_{ 2 }^{ 4 } 2 dx \\ = ( x ^ 2 - 2x ) \mid _ 0 ^ 2 + 2x \mid _ 2 ^ 4 = [ ( 4 - 4 ) - ( 0 - 0 ) ] + [ 8 - 4 ] = 4 $$
روش دیگری نیز برای حل انتگرال فوق وجود دارد. با رسم نمودار تابع $$ x - | x - 2 | $$ در محدوده صفر تا ۴ و محاسبه مساحت زیر نمودار، به راحتی میتوانیم انتگرال این تابع در محدوده داده شده را بهدست آوریم. همانطور که اشاره شد، تابع به صورت زیر تعیین علامت میشود:
$$ f (x ) = \begin{cases} x- | x -2 | = 2x -2 & 0 <x < 2 \\ x - | x - 2 | = 2 & 2 < x < 4 \end{cases}$$
تابع در محدوده $$0 <x < 2$$& خط مستقیمی با شیب مثبت است که از نقطههای $$(0 , -2 ) $$ و $$(2 , 2 ) $$ میگذرد و محور $$x $$ را در نقطه یک، قطع میکند. همچنین، برای $$2 < x < 4 $$، تابع خطی موازی محور $$x $$ است که از نقطه $$( 0 , 2 ) $$ عبور میکند.
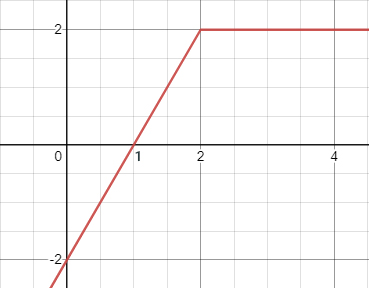
برای محاسبه انتگرال این تابع در محدوده صفر تا چهار، مساحت قسمت مشخص شده در تصویر زیر را بهدست میآوریم:
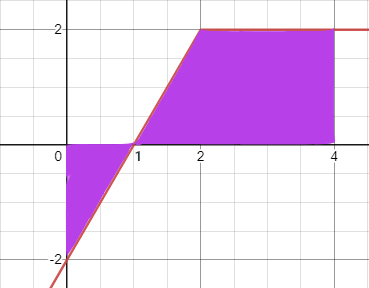
مساحت مثلث برابر است با:
$$S_ 1 = \frac { -2 \times 1 } { 2 } = -1 $$
نساحت ذوزنقه نیز برابر است با:
$$S _ 2 = \frac { (3 + 2 ) \times 2 } { 2 } = 5 $$
مساحت کل زیر نمودار برابر است با:
$$S = S _ 1 + S _2 = -1 + 5 = 4 $$
مشتق انتگرال زیر نسبت به $$x$$ برابر است با:
$$\int_{3 x ^ 2 }^{ -1 } \frac { e ^ t - 1 } { t } dt$$
$$\frac { 2 - 2 e ^ { 3 x ^ 2 } } { 2x }$$
$$\frac { 2 - 2 e ^ { 3 x ^ 2 } } { x }$$
$$\frac { 2 - 2 e ^ { x ^ 2 } } { x }$$
$$\frac { 1 - e ^ { 3 x ^ 2 } } { x }$$
ابتدا حد بالا و پایین انتگرال را با یکدیگر جابجا میکنیم، به گونهای که عدد ۱- حد پایین و $$3 x ^ 2 $$ حد بالا باشد. مشتق $$\int_{3 x ^ 2 }^{ -1 } \frac { e ^ t - 1 } { t } dt$$ نسبت به $$x$$ برابر است با:
$$\frac{\text{d}}{\text{d}x}[\int_{3 x ^ 2 }^{ -1 } \frac { e ^ t - 1 } { t } dt ] = \frac{\text{d}}{\text{d}x}[- \int_{-1 }^{ -3 x ^ 2 } \frac { e ^ t - 1 } { t } dt ] = - ( 6 x ) \frac { e ^ { 3 x ^ 2 } - 1 } { 3 x ^ 2 } = \frac { 2 - 2 e ^ { 3 x ^ 2 } } { x }$$











سلام از سایت فرادرس واقعا دستتون درد نکنه من که ریاضی اصلا بلد نبودم با سایت شما خیلی خوب دارم یاد میگیرم مطالبتون خیلی روان ساده و خوب بیان شده تشکر
مرسی واقعااااا
یه ترم گذشت ما سر کلاس هیچی از این انتگرال نفهمیدیم … ممنون از توضیح روون و عالی تون
سلام از نظر فرمولی و محاسبات زیر نمودار 2t در ثانیه مثلاً سوم ۶ لیتر به مخزن وارد می شود و حجم ۹ لیتر است ولی برای من یک پارادوکس ذهنی پیش امده و مانند دوست عزیزی که در پایین گفته باید در ثانیه ۴ مقدار ۲۰ لیتر آب در مخزن باشد ولی جواب 16 است گفتید حجم خطی نیست من خطی را نفهمیدم ذهن من هم می گوید در ثانیه اول ۲ لیتر آب به مخزن ریختم ثانیه دوم ۴ لیتر در مخزن ریختم تا حالا می شود ۶ لیتر در ثانیه سوم ۶ لیتر به مخزن ریختم تا حالا می شود ۱۲ لیتر در ثانیه چهارم 8 لیتر به مخزن ریختم تا حالا باید 20 لیتر آب جمع شده باشد ولی فرمول ها می گویند 16لیتر لطفاً این پارادوکسی که برای من ایجاد شده کسی پاسخ دارد تشکر
با سلام و وقت بخیر؛
پاسخ دادن به سوال شما، نیازمند صحبت در مورد مفهوم غیرخطی «نرخ» (Rate) و تفاوت آن با مفاهیم خطی دیگر مانند «سرعت» (Velocity) است. نرخ، به صورت میزان تغییرات یک واحد نسبت به واحد دیگر (معمولا زمان) تعریف میشود. به عنوان مثال، وقتی از شتاب یک جسم صحبت میکنیم، منظور ما نرخ افزایش یا کاهش سرعت بر واحد ثانیه است. اگر شتاب جسمی که از حالت سکون شروع به حرکت میکند برابر با ۱ متر بر مجذور ثانیه باشد، آن جسم پس از ۱ ثانیه، ۰/۵ متر، پس از ۲ ثانیه، ۲ متر و پس از ۳ ثانیه، ۴/۵ متر را طی خواهد کرد (رابطه بین شتاب و جابجایی خطی نیست که با ضرب کردن زمان در آن بتوان میزان جابجایی را به دست آورد). مثال ۲ این مقاله، در مورد نرخ تغییرات جریان صحبت کرده و رابطه آن با زمان را به صورت Q=2t تعریف میکند. توجه کنید که این رابطه، نرخ (افزایش یا کاهش سرعت) پر شدن مخزن را نمایش میدهد. ما در مورد نرخ پر شدن صحبت میکنیم نه سرعت پر شدن. برای درک بهتر موضوع، به این سوال پاسخ دهید: یکای نرخ جریان چیست؟ لیتر بر ثانیه. اکنون نرخ جریان در ثانیه اول را محاسبه کنید. به چه جوابی رسیدیم؟ نرخ جریان در ثانیه ۱، برابر با ۲ لیتر بر ثانیه است. دقت داشته باشید که جواب شما، ۲ لیتر نیست، ۲ لیتر بر ثانیه است. اکنون، به این سوال پاسخ دهید: یکای حجم مخزن چیست؟ لیتر. ما در مثال ۲، یک فرمول داریم که خروجی آن، یکای لیتر بر ثانیه را میدهد. برای اینکه بتوانیم با استفاده از آن، حجم مخزن را به دست بیاوریم، از این رابطه بر حسب زمان (t) انتگرال میگیریم تا بعد رابطه از لیتر بر ثانیه به لیتر تغییر کند. به طور خلاصه، جوابی که در اینجا به دست آوردهاید (عدد ۲۰
لیتر) در واقع ۲۰ لیتر بر ثانیه است و نمیتوان آن را به عنوان حجم (لیتر) در نظر گرفت.از همراهی شما با مجله فرادرس سپاسگزاریم
سلام و عرض ادب
من بعد مدتها تصمیم گرفته ام مجددا ریاضی بخوانم . آنهم از ابتدا. و از آنجا که باید با دلیل و منطق پیشروی کنم تا مطالب را خوب درک کنم.این شد که مجبور شدم سوال بنویسم.
در مثال دوم
زمانی که مثلا در ثانیه سوم ! ۶ لیتر آب در ثانیه عبور کرده و به مخزن ریخته شده است ! پس قاعدتا و طبق هر دلیل و برهانی باید ۶ لیتر آب در مخزن باشد. و در ثانیه چهارم ۴ هم قطعا باید ۸ لیتر آب در مخزن باشد.
ولی چرا حجم بدست آمده در زمان سوم ۹ لیتر و در زمان ۴ برابر ۱۶ لیتر است.
بهرحال نرخ عبور متغیر نیست و کاملا مشخص است. مگر اینکه هر لحظه فشار آب هم بیشتر بشود.
آیا اشتباه میکنم ؟
واقعا یه بخش عظیمی از دانسته های خودمو مدیون فرادرس هستم ( به خصوص جناب آقای مجید عوض زاده ).
یک دنیا ممنون.
سلام ع من برنامه شما را تعقیب میکنم سپاس اززحمات تان خیلی مفید تمام گشته برایم امید است تا ویدیوها انتگرال معین را نیز در دسترس مان قرار دهید وسلام
با سلام؛
خوشحالیم که مطالب مجله فرادرس برای شما مفید بوده است.
با تشکر از همراهی شما با مجله فرادرس
عالی بود
مرسییی خیلی خوب توضیح دادین🌸✨
سلام ممنونم .خیلی عالی بود.من فقط یک سوال داشتم.میخواستم بدونم نیوتن چطوری متوجه شد که انگرال گیری و مشتق گیری عکس هم هستن.و چطور متوجه شد که با بدست اوردن تابع اولیه و جاگذاری بازه میشه مسات زیر نمودار رو خیلی راحت بدست اورد؟ممنونم
دقت کنید در ثانیه سوم نرخ جریان آب 6لیتر بر ثانیه است نه اینکه تا ثانیه سوم فقط 6لیتر آب خارج شده.
امیدوارم مطلب و رسونده باشم
خیللی عالی است برنامه تان سپاس بسبار از خدمت تان
به این دید نگاه کنید که مشتق تفاضل کلی نقطه و انتگرال جمع کلی نقطه هستش.
من هم همین موضوع را متوجه نشدم که چطور مشتق و انتگرال میتوانند عکس هم باشند در حالی که مشتق شیب نمودار و انتگرال مساحت زیر نمودار میباشد؟
عالی بود 🙂
عالی بود مرسی ازتون:)
عالی بود مرسی.خیلی خوب بود خداقوت
با سپاس از مثالی که زدید و بسیار زیبا تحلیل شد… ممنون از فرادرس
عالی بود مرسی
ویدیو های اموزشی انتگرال معین را در دسترس مان قرار دهید
خیلی عالی متشکر
عالی
من سیزدہ سالمہ و کامل فھمیدم ممنون
مطالب بسیار قابل فهم ودرک توضیح داده شده ممنون از شما
واقعا نمیدونم چطوری ازتون تشکر کنم
سلام
لطفاً در صورت امکان در مورد محاسبه تعداد حالات ممکن تهیه 12000 تومان با استفاده از سکه های 200 و 500 تومانی راهنمایی بفرمایید.
همچنین چگونه می شود با استفاده از انتگرال گیری از زیر ناحیه 12000 و دو خط برای سکه های 500 و 200 تومانی به نتیجه رسید؟
سلام برای حل این سوال باید بدونیم که ۲۰۰ رو جوری استفاده کنید که ضرب در مضرب ۵ باشه چرا که در غیر این صورت عدد مورد نظر رو نمیسازه خب حالا ما اینجوری حساب میکنیم ۰ تا ۲۰۰ بقیش ۵۰۰ ۵ تا ۲۰۰ بقیش ۵۰۰. ۱۰ تا ۲۰۰ بقیش ۵۰۰ و…. تا به ۱۲۰۰۰ برسی میشه حالت های ممکنت
این مسئله رو میشه با استفاده از معادله سیاله حل کرد
سلام ، این مسئله اول به سادگی با معادله سیاله قابل حل است
بسیار خوب بود سپاس
یک جهان سپاس و تشکر از شما به خاطر مطالب ارزشمندی که در سایت تان درج می نمایید تا همگان استفاده نمایند. موفق و موئد باشید
سلام من بیشتر مطالب فرادرسو دنبال میکنم و خیلی برام مفیده فقط لطفا صدای موزیک متنو کمتر کنید و بجای خواندن از روی راه حل ها تایپشون کنید سپاس
بسیار عالی بود. خیلی وقت بود که دنبال یه مطلب جامع برای انتگرال بودم. بازهم از ریاضی و بحث دیفرانسیل و انتگرال مطلب بذارید
واقعا عالی
خیلی خیلی دستتون درد نکنه
بسیار عالی بود وارزش دیدن وخواندن مطالب را داشت
خیلی عالی بود تشکر
بسمه تعالی عالی بود سپاس
۲۰
عالی عالی …ممنونم
لطفاً نگاه دقیق تری بندازید و اگه نمیتونید بهتر هست که بگید؛ xبه توان دو انتگرالش میشه یک دوم ضربدر x
نه جواب 2x میشه
سلام این ویدئو ها کامل یاد میدن انتگرال هارو؟
عالی
جواب انتگرال w^2.r/g dr چیست
با سلام؛ در تصویر زیر نحوه محاسبه این انتگرال ارائه شده است.
خیلی خوب بود
ممنون
با سلام.. ببخشید من در مورد بازه انتگرال سوال داشتم. که برای X>0 و Y>0 و X+Y<2 بازه انتگرال گیری برای محاسبه مساحت چی میشه؟؟
عالیییییی. همش تو فکر انتگرال دوگانه بودم
با سلام و تشکر از توجه شما.
این نامساوی نشان دهنده ناحیه محدود به محورهای مختصات و تابع y=2-x است. لذا برای محاسبه آن باید از بازه ۰ تا ۲ از این تابع انتگرال گرفته شود. در تصویری که در ادامه ارائه شده، روند حل مسئله توضیح داده شده است.
مگه میشه به این سادگیی انتگرال رو توضیح داد عالی عالی عالی
سلام سایتتون رو بوکمارک کردم برام جالبه که جواب سوالات رو هم میدید ! دنبال یه چیزی میگشتم که شروع کنم به خوندنش تا بفهمم این فرمول هایی که حفظ کردم برای چیه ؟ گلی
با تشکر از توضیحات خوبتان فقط من یک چیز رو در مثال مخزن متوجه نمی شوم، با توجه به فرمول نرخ ورد آب مجموع آب وارد شده به مخزن
طی 4 ثانیه میشود 8+6+4+2 که میشود 20 لیتر آب پس چجوری حجم مخزن 16 میشود؟
سلام
حجم آب ورودی در ثانیه ۴فقط برابر ۸لیتر بر ثانیه است تو هر ثانیه ۲ لیتر اضافه میشه وبرای به دست آوردن انتگرال کافیه اونو یک مستطیل ۴در ۸در نظر بگیرم و تقسیم بر ۲کنیم یا به عبارتی از مثلث انتگرال بگیریم
چیزی که شما محاسبه کردید یعنی اینکه سرعت ورود آب به مخزن در طول هر ثانیه ثابت باشه در حالیکه اینطور نیست و سرعت در هر لحظه تابع زمانه، اگه بصورت ترسیمی چیزی که نوشتید رو نشون بدید یک نمودار پله ای میشه که با تابع 2t کاملاً متفاوته، البته اینم بگم که روش شما همون اصول پایه انتگراله و در واقع شما فرمول انتگرال ریمان رو نوشتید ولی چون تقسیم بندی زمانی شما 1 ثانیه ای بوده، باعث خطای بوجود اومده شده، اگه فواصل زمانی رو کوچیکتر کنید میبینید اختلافش با عدد 16 کمتر میشه و جواب به سمت جواب صحیح میل میکنه.
با سلام و ممنون از بازخورد ارائه شده.
روشی که شما استفاده کردهاید درست و البته جالب است. اما توجه داشته باشید که تنها در صورت افزایش حجم به صورت خطی، میتوان از این روش استفاده کرد. برای نمونه اگر نرخ ورود جریان به مخزن برابر با ۲ باشد، میزان حجم آب پس از ۴ ثانیه برابر با ۲+۲+۲+۲=۸ میشود که برابر با حاصل انتگرال است.
معرکه بود
عااااالی عالی.خیلی مممنون
خدا خیرتان دهد
خدا پدرومادرتان را بیامرزد
خداپدرومادرتو بیامرزه عالی بود
عمقی وساده
مرسی از آموزش خودتان با اینکه رشته ام علوم انسانی ولی خداروشکر متوجه شدم
سلام ممنون بابت توضیحات خوبتون
ساده، مفید و قابل فهم بود.