اعداد موهومی: راهنمای تصویری و شهودی – به زبان ساده

اعداد موهومی باعث سردرگمی افراد زیادی می‌شوند. موضوعات دیگری مانند عدد اویلر نیز این چنین هستند. در این گونه موارد دو حالت بیشتر وجود ندارد. یا آن موضوع یک مسئله انتزاعی ریاضیاتی است و می‌توان با تابع حل کرد که در این حالت می‌توان آن را با بررسی بیشتر درک کرد. در حالت دوم، موضوع در حیطه مباحث پیشرفته قرار دارد و بهتر است یادگیری آن را به دوره دانشگاه موکول کنید.

ما در این مطلب نیز مانند نوشته‌های دیگری که در سلسله مطالب ریاضیات به زبان ساده ارائه کردیم از رویکردهای زیر بهره خواهیم گرفت:

• روی رابطه‌ها متمرکز می‌شویم و نه فرمول‌های مکانیکی.
• اعداد مختلط را به صورت یک ارتقا برای سیستم عددی کنونی تصور می‌کنیم. با این نگاه، عدد صفر، اعداد اعشاری و اعداد منفی نیز صرفاً نوعی ارتقای سیستم عددی محسوب می‌شوند.
• از نمودارهای تصویری استفاده خواهیم کرد و برای درک آینده صرفاً به متن اکتفا نمی‌کنیم.

در این مسیر ما یک سلاح مخفی داریم که «یادگیری از طریق مقایسه» است. در واقع اعداد موهومی را با مشاهده اجدادشان یعنی اعداد منفی یاد خواهیم گرفت.

درک واقعی اعداد منفی

اعداد منفی موضوع آسانی نیستند. تصور کنید که یک ریاضیدان اروپایی در قرن 1700 میلادی هستید. شما با اعداد 3 و 4 آشنا هستید و می‌دانید که 1 = 3 - 4 است. اما آیا معنی 4 - 3 را نیز می‌دانید؟ مسلماً در آن زمان از خود سؤال می‌کردید که آیا چنین چیزی معنی هم دارد؟ چگونه می‌توان 4 تا از 3 چیز کسر کرد؟ چگونه می‌توان چیزی کمتر از هیچ داشت؟

اعداد منفی عجیب به نظر می‌رسند. به قول ریاضیدان قرن شانزدهمی، فرانسیس ماسرز (Francis Maseres) «اعداد منفی موجب ایجاد ابهام در کل نظام معادلات شده‌اند». با این حال، امروزه این فکر که اعداد منفی منطقی یا مفید نیستند، عجیب محسوب می‌شود!

سؤال این است که چه شد که اعداد منفی ایجاد شدند؟ در واقع ما اعدادی را به صورت نظری ابداع کرده‌ایم که خصوصیات مفیدی دارند. اعداد منفی چیزی نیستند که بتوان آن‌ها را لمس کرد یا به طور عملی مشاهده نمود؛ اما روابط خاصی (مانند بدهی) را توصیف می‌کنند و این یک خصوصیت مفید است.

در واقع به جای این که بنویسیم «من به شما 30 تومان بدهکارم» و برای درک رابطه مالی نیازمند خواندن کلمات باشیم، می‌توانیم صرفاً بنویسیم «30-» و بدانیم که ما در سمت بدهکار رابطه هستیم. اگر درآمدی کسب کنیم و بدهی‌مان را پرداخت کنیم، این تراکنش را با استفاده از اعداد منفی می‌توانیم به راحتی به صورت زیر ثبت کنیم:

-30 + 100 = 70

بدین ترتیب متوجه می‌شویم که پس از پرداخت بدهی همچنان 70 تومان داریم.

علامت‌های مثبت و منفی به طور خودکار جهت را نشان می‌دهند و دیگر به جمله‌ای برای توصیف تأثیر هر تراکنش نیاز نداریم. بدین ترتیب محاسبات ریاضیاتی آسان‌تر و منظم‌تر می‌شود. دیگر مهم نیست که اعداد منفی قابل لمس هستند یا نه، چون همین قدر که خصوصیات مفیدی دارند کافی است و می‌توان آن‌ها را تا حدی که به صورت موارد ضروری برای محاسبات روزمره مطرح شوند مورد استفاده قرار داد. امروزه اگر ببینیم کسی از اعداد منفی استفاده نمی‌کند، برای ما بسیار عجیب خواهد بود.

ما با این حرف قصد نداریم تلاشی که برای ابداع اعداد منفی صورت گرفته است را ناچیز بشماریم. مطرح شدن و رواج یافتن استفاده از اعداد منفی نیازمند یک تغییر ذهنی بزرگ بوده است. حتی فردی مانند اویلر که ریاضیدان نابغه‌ای محسوب می‌شود و عدد e و موارد بسیار زیاد دیگری را کشف کرده است، اعداد منفی را آن گونه که امروزه ما درک می‌کنیم، نشناخته است. در آن زمان اعداد منفی نتایجی «بی‌معنی» شمرده می‌شدند.

این که از کودکان امروزی انتظار می‌رود چیزهایی را درک کنند که زمانی باعث سردرگمی ریاضیدان‌های قدیم می‌شد، نشان‌دهنده ظرفیت بالای ذهنی ما است.

ورود به قلمروی اعداد موهومی

اعداد موهومی نیز داستانی مشابه اعداد منفی دارند. ما معادله‌ای مانند زیر را می‌توانیم به راحتی حل کنیم:

$$x^2 = 9$$

پاسخ آن 3 و 3- است، اما فرض کنید فردی یک تغییر کوچک در معادله فوق به صورت زیر ایجاد کند:

$$x^2 = -9$$

همین تغییر کوچک موجب می‌شود که اغلب افراد وقتی این معادله را می‌بینند دچار وحشت شوند. در واقع ما می‌خواهیم جذر عددی کمتر از صفر را محاسبه کنیم. این عجیب است. البته در طی تاریخ افراد مختلفی تلاش کرده‌اند برای این سؤال پاسخی بیابند، اما در این نوشته برای سادگی از اشاره به موارد تاریخی حذر می‌کنیم.

معادله فوق عجیب به نظر می‌رسد، همان‌طور که اعداد منفی، صفر و اعداد گنگ نیز روزی عجیب به نظر می‌رسیدند. اما آیا هیچ معنای «حقیقی» برای سؤال فوق وجود ندارد؟

پاسخ این است که معنای حقیقی وجود دارد. به همین دلیل «اعداد موهومی» به اندازه هر عدد دیگری معمولی هستند. در واقع اعداد موهومی ابزاری برای توصیف دنیا هستند. همان طور که اعدادی مانند 1-، 0.3 و 0 «وجود دارند»، می‌توان تصور کرد که عددی مانند i وجود دارد که:

$$i^2 = -1$$

توضیح آن این است که i را در خودش ضرب می‌کنیم تا عدد 1- به دست آید. شاید در ابتدا دچار سردرگمی شوید؛ اما اگر تلاش کنید تصور کنید عدد i وجود دارد، باعث می‌شود که این معادله در ذهنتان آسان‌تر شود. بدین ترتیب روابط جدیدی ظاهر می‌شوند.

شما ممکن است به i اعتقادی نداشته باید، همان طور که برخی از ریاضیدان‌های قدیمی اعتقادی به 1- نداشتند. درک مفاهیم پیچیده و جدید، دشوار است و ممکن است در ابتدا معنای مشخصی حتی برای فردی مانند اویلر نداشته باشند. اما همان طور که در مورد اعداد منفی دیدیم، مفاهیم غریب نیز می‌توانند همچنان مفید باشند.

شاید برخی افراد عبارت «اعداد موهومی» را نپسندند، چون باعث گمراهی ذهن می‌شود. عدد i به همان اندازه اعداد دیگر نرمال است؛ اما صفت موهومی باعث می‌شود چنین به نظر نرسد.

درک بصری از اعداد منفی و مختلط

همان طور که قبلاً دیدیم، $$x^2 = 9$$ در واقع به معنی زیر است:

$$1 . x^2 = 9$$

یا

$$1 . x . x = 9$$

چه تبدیلی روی x صورت می‌گیرد که وقتی دو بار انجام می‌یابد آن را به 9 تبدیل می‌کند؟

فیلم آموزش محاسبات عددی با متمتیکا Mathematica – مقدماتی در فرادرس

کلیک کنید

دو پاسخ وجود دارد: x = 3 و x = -3 یعنی هم می‌توان 3 برابر کرد و هم 3 برابر کرد و بعد معکوس نمود. معکوس کردن یک تفسیر از ضرب در عدد منفی محسوب می‌شود.

اینک فرض کنید $$x^2 = -1$$ باشد، که در واقع به معنی زیر است:

$$1 . x . x = -1$$

چه تبدیلی روی x صورت می‌گیرد که وقتی دو بار انجام می‌یابد آن را به 1- تبدیل می‌کند؟

نکات زیر را می‌دانیم:

• ما نمی‌توانیم یک عدد مثبت داشته باشیم، چون وقتی در خودش ضرب ‌شود، همچنان مثبت خواهد بود.
• ما نمی‌توانیم عدد منفی داشته باشیم، چون وقتی در خودش ضرب شود، نتیجه باز هم عددی مثبت خواهد بود.

اما اگر این تبدیل را نوعی چرخش تصور کنیم چطور؟ گرچه ممکن است عجیب به نظر بیاید؛ اما اگر تصور کنیم x همان «چرخش 90 درجه» باشد، در این صورت اعمال دوباره x به معنی یک چرخش 180 درجه و معکوس کردن 1 به صورت 1- است.

چرخش اعداد موهومی

اگر کمی در این مورد بیشتر تأمل کنید، درمی‌یابیم که با اعمال چرخش دوگانه در جهت معکوس (ساعتگرد) نیز از 1 به 1- می‌رسیم. این چرخش منفی یا ضرب در i- است.

اگر 1 را دو بار در i- ضرب کنیم، در ضرب نخست 1 به i- ضرب می‌شود و در ضرب دوم i- به 1- تبدیل می‌شود. از این رو در واقع دو جذر برای -1 به صورت i و i- وجود دارد.

این نتیجه کاملاً جالب است. اینک نوعی پاسخ برای سؤال خود یافته‌ایم؛ اما این پاسخ‌ها واقعاً به چه معنا هستند؟

• i «یک بعد موهومی جدید» برای اندازه‌گیری عدد است.
• i (یا i-) چیزی است که هنگام چرخش عددها به دست می‌آید.
• ضرب کردن در i به معنی چرخش 90 درجه‌ای در جهت پادساعتگرد است.
• ضرب کردن در i- به معنی چرخش 90 درجه‌ای در جهت ساعتگرد است.
• دو چرخش در هر جهت به عدد 1- می‌رسد. بدین ترتیب دوباره به بعد معمولی اعداد مثبت و منفی می‌رسیم.

اعداد 2 بعدی هستند

شاید این بینش جدید از اعداد به نظر عجیب بیاید، همان‌طور که اعداد اعشاری یا تقسیم دارای باقیمانده، احتمالاً برای رومیان باستان عجیب بوده است. شاید در آن روزگار یک رومی به دیگری گفته باشد: «منظورت چیست که عددی بین 1 و 2 وجود دارد؟» این بینش عجیب، روشی جدید برای تفکر در مورد ریاضیات است.

ما پرسیدیم که چگونه می‌توان در دو مرحله 1 را به 1- تبدیل کرد و پاسخی برای آن بدین صورت یافتیم، که آن را به میزان 90 درحه بچرخانیم. این مسئله عجیبی است و روش جدیدی برای اندیشه در مورد مسائل ریاضی محسوب می‌شود؛ اما با این حال مفید است. در هر صورت تفسیر هندسی از اعداد مختلط تا دهه‌ها پس از کشف i ارائه نشده است.

همچنین به خاطر داشته باشید این که پادساعتگرد را مثبت در نظر می‌گیریم، یک تفکر قراردادی است و می‌توان به سادگی معکوس آن را تصور کرد.

یافتن الگوها

در این بخش به بررسی جزییات می‌پردازیم. وقتی اعداد منفی (مانند 1-) را ضرب می‌کنیم، الگویی به صورت زیر داریم:

1، -1 1، -1، 1، -1، 1، -1

از آنجا که 1- اندازه عدد را تغییر نمی‌دهد و فقط علامتش عوض می‌شود، یک حرکت رو به جلو و عقب را شاهد هستیم. برای هر عدد به صورت x داریم:

x, -x, x, -x, x, -x…

این ایده مفید است و عدد x را می‌توان نوعی نماینده هفته‌های خوب و بد دانست. فرض کنید به طور پشت سرهم یک هفته‌ی خوب و یک هفته‌ی بد را شاهد هستید، اگر این هفته خوب بوده باشد، در این صورت هفته 47 چگونه خواهد بود؟

$$x . (-1)^{47} = x . -1 = -x$$

بدین ترتیب x- به معنی یک هفته بد است. دقت کنید که اعداد منفی چگونه ترتیب علامت‌ها را حفظ می‌کنند. بدین ترتیب می‌توان (-1)^47 را در یک ماشین حساب به سرعت محاسبه کرد و لازم نیست یکی یکی هفته‌های خوب و بد را بشماریم. چیزهایی که حرکت نوسانی رفت و برگشت دارند، به خوبی به وسیله اعداد منفی قابل مدلسازی هستند.

اینک چه می‌شود اگر به ضرب کردن در i ادامه دهیم؟

$$1 , i^2, i^3, i^4, i^5$$

نکته جالبی وجود دارد. این وضعیت را کمی تشریح می‌کنیم:

• 1=1 - بحثی وجود ندارد.
• i = i - در این مورد هم کاری نمی‌توان انجام داد.
• $$i^2 = -1$$ - این نقطه شروع تعریف i است.
• $$i^3 = (i.i).i = -1.i = -i$$  بدین ترتیب 3 چرخش پادساعتگرد برابر با 1 چرخش ساعتگرد است.
• $$i^4 = (i.i).(i.i) = -1.-1 = 1$$ همچنین 4 چرحش باعث می‌شود یک دور کامل روی دایره بزنیم.
• $$i^5 = i^4. i = 1.i = i$$ اینک دوباره به i رسیده‌ایم.

اگر بخواهیم مباحث فوق را به صوت بصری ارائه کنیم:

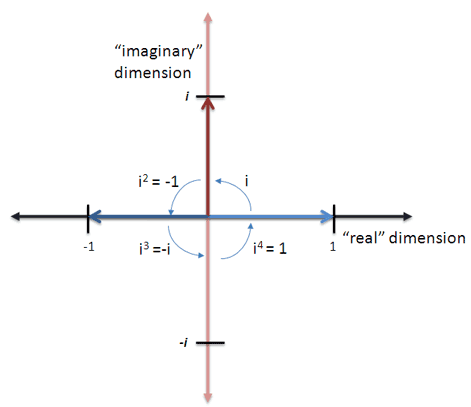
بدین ترتیب 4 چرخش داریم. هر کس می‌تواند ببیند که با 4 چرخش به جای اول رسیده‌ایم، گویی هیچ چرخشی نبوده است. اینک به جای تمرکز روی اعداد موهومی (i, i^2) به الگوی کلی زیر توجه کنید:

X, Y, -X, -Y, X, Y, -X, -Y…

مانند اعداد منفی می‌بینم که اعداد موهومی نیز یک حرکت رفت و برگشت را نشان می‌دهد. با استفاده از اعداد موهومی می‌توان هر چیزی را که بین دو بعد X و Y می‌چرخد یا هر چیزی که رابطه چرخه‌ای، مدور و مانند آن دارد مدلسازی کنیم.

درک اعداد مختلط

جزییات دیگری نیز وجود دارند که باید بررسی کنیم. آیا یک عدد می‌تواند هم «حقیقی» و هم «موهومی» باشد؟

چه کسی گفته است که ما باید به اندازه کل 90 درجه چرخش بکنیم؟ اگر مقداری روی محور اعداد حقیقی و مقداری نیز روی محور موهومی حرکت کنیم، وضعیتی مانند تصویر زیر به دست می‌آید:

اینک ما در زاویه 45 درجه قرار داریم و بخش‌های حقیقی و موهومی عدد (1 + i) با هم برابر هستند. مثل این که روی یک ساندویچ هات‌داگ، هم سس خردل و هم کچاپ زده باشید. چه کسی گفته است باید یکی از آن دو را انتخاب کرد؟

در واقع با انتخاب هر ترکیبی از اعداد حقیقی و موهومی می‌توان یک مثلث ساخت. این زاویه، «زاویه چرخش» نام دارد. یک عدد مختلط نام جذابی برای اعدادی است که هم بخش حقیقی و هم موهومی دارند. این اعداد به صورت a + bi نوشته می‌شوند که:

• a بخش حقیقی عدد است
• و b بخش موهومی آن است.

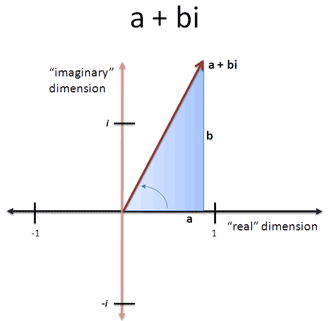
چندان بد نیست؛ اما سؤال دیگری نیز هست: یک عدد مختلط تا چه حد می‌تواند «بزرگ» باشد؟ بخش حقیقی یا بخش‌های موهومی را به صورت مستقل از هم نمی‌توان اندازه‌گیری کرد، چون در این صورت کلیت عدد از بین می‌رود.

اگر یک گام به عقب بازگردیم، می‌بینیم که اندازه اعداد منفی، ربطی به شماره آن‌ها ندارد و به فاصله‌ای که از صفر می‌گیرند بستگی دارد. در مورد اعداد منفی به صورت زیر محاسبه می‌شود:

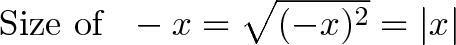
که روش دیگری برای یافتن قدر مطلق است. اما در مورد اعداد مختلط، چگونه می‌توان دو مؤلفه زاویه 90 درجه را محاسبه کرد؟

قضیه فیثاغورس چاره کار است. این قضیه در همه جا کاربرد دارد، حتی در اعدادی که 2000 سال پس از خود فیثاغورس اختراع شده‌اند. ما در اعداد مختلط، نوعی مثلث ایجاد می‌کنیم و وتر مثلث میزان فاصله از صفر را معین می‌کند:

با این که تعیین اندازه مانند اعداد منفی به اندازه «حذف علامت منفی» آسان نیست؛ اما اعداد مختلط نیز کاربردهای خاص خود را دارند. در ادامه این کاربردها را بررسی می‌کنیم.

یک مثال واقعی: چرخش‌ها

برای استفاده از اعداد موهومی لازم نیست تا زمان دانشگاه صبر کرد. آن‌ها را می‌توان در زندگی روزمره نیز مشاهده کرد. موارد زیادی در مورد اعداد مختلط می‌توان گفت؛ اما همین قدر به خاطر داشته باشید که:

ضرب کردن در یک عدد مختلط، به معنی چرخش دادن به اندازه زاویه آن است.

فرض کنید روی یک قایق باشیم که در حال حرکت به صورت 3 واحد به سمت شرق و 4 واحد به سمت شمال است. اگر بخواهیم حرکت خود را 45 درجه در جهت پادساعتگرد تغییر دهیم، جهت جدید چگونه خواهد بود؟

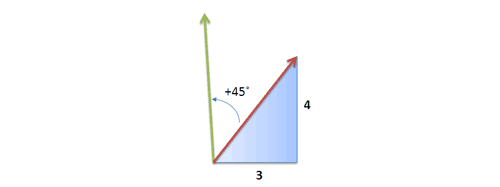
شاید فکر کنید می‌توان با استفاده از مثلثات و محاسبه سینوس و کسینوس و ... این مقدار را محاسبه کرد. اما این موارد به ماشین حساب نیاز دارند.

روش ساده‌تری نیز برای پاسخ دادن به سؤال فوق وجود دارد. ما در جهت 3 + 4i قرار داریم و برایمان مهم نیست که بدانیم چه زاویه‌ای است و می‌خواهیم 45 درجه به سمت چپ بچرخیم. می‌دانیم که 45 درجه برابر با 1 + i است (کاملاً قطری) و از این رو می‌توانیم آن را در مقدار خود ضرب کنیم.

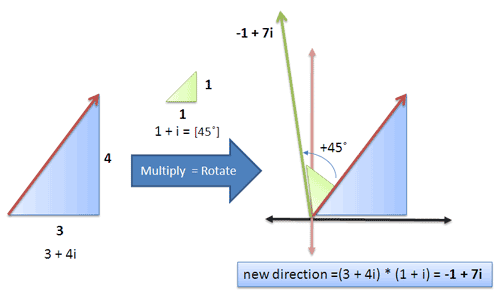
توضیح پاسخ فوق چنین است که:

• جهت‌گیری اصلی به صورت 3 واحد شرقی و 4 واحد شمالی است: 3 + 4i
• به میزان 45 درجه در جهت پادساعتگرد می‌چرخیم، یعنی در 1 + i ضرب می‌کنیم.

اگر این دو مقدار را در هم ضرب کنیم:

بنابراین جهت‌گیری جدید ما 1 واحد غربی (1- شرقی) و 7 واحد شمالی است.

می‌بینید که چطور در کمتر از چند ثانیه، راه‌حل سؤال فوق را بدون استفاده از سینوس و کسینوس یافتیم. بدین ترتیب لازم نیست از هیچ بردار یا ماتریس استفاده کنیم و یا توجه کنیم که اینک در کدام ربع دایره مثلثاتی قرار داریم و صرفاً از جبر برای ضرب فوق استفاده کردیم. اعداد موهومی قواعد چرخش را نشان می‌دهند و بدین ترتیب از عملکرد صحیح آن‌ها مطمئن می‌شویم.

نکته جالب‌تر این است که نتیجه محاسبه فوق مفیدتر است. ما دریافتیم که باید جهت (1,7-) را انتخاب کنیم و درجه آن را محاسبه نکردیم. البته با توجه به این که در ربع دوم قرار داریم، می‌دانیم که atan(7/-1) = 98.13 درجه است. اما اگر بخواهیم این زاویه را به صورت دقیقی رسم کنیم چگونه می‌توانیم عمل بکنیم؟ آیا باید همیشه نقاله همراه خود داشته باشیم؟

می‌توانیم زاویه فوق را به صورت سینوس و کسینوس (به ترتیب 0.14- و 0.99) دربیاوریم و نسبت معقولی بین آن‌ها (حدود 1 و 7) بیابیم و مثلث را ترسیم کنیم. البته اعداد مختلط همین نسبت را بی‌درنگ، دقیق بدون نیاز به ماشین حساب قبلاً به ما نشان داده بودند.

این روش شگفت‌انگیزی است. البته مثلثات نیز بسیار مفید است؛ اما اعداد مختلط می‌توانند محاسبات پیچیده‌ای مانند
(cosine(a+b را ساده کنند. این تنها یک کاربرد ساده است و در مقالات بعدی کاربردهای بیشتری را معرفی خواهیم کرد.

در این نوشته به معرفی اعداد مختلط پرداختیم و اینک باید درک مناسبی از آن‌ها داشته باشید. موارد زیاد دیگری هستند که می‌توان مورد بررسی قرار داد؛ اما برای این نوشته تا همین حد کافی است و این موارد بیشتر را به مقالات آینده موکول می‌کنیم. هدف ما ساده است:

• شما را قانع کنیم که اعداد مختلط گرچه عجیب به نظر می‌رسند؛ اما می‌توانند همانند اعداد منفی مفید باشند.
• به شما نشان دهیم که اعداد مختلط می‌توانند مسائل مشخصی مانند چرخش‌ها را به شیوه‌ای ساده‌تر حل کنند.

برای خیلی از افراد، اعداد موهومی همواره به صورت یک کابوس بوده است و فاقد هر گونه بینش شهودی در مورد آن بوده‌اند. اما هر کس با هر سطح از دانش با مطالعه این راهنما باید درک شهودی خوبی از این اعداد داشته باشد. ضرب‌المثل مشهوری وجود دارد که «به جای نفرین کردن تاریکی، شمعی روشن کن»

سخن پایانی: اعداد مختلط همچنان عجیب هستند

البته که اعداد مختلط ذاتاً پیچیده و عجیب هستند. ما تلاش کردیم خود را به جای کسی قرار دهیم که نخستین بار عدد صفر را کشف کرده است.

فیلم مجموعه آموزش ریاضیات – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

صفر ایده بسیار عجیب و غریبی است، «چیزی» را برای نشان دادن «هیچ چیز» تعیین کنیم و این نکته‌ای است که رومی‌ها از آن طفره می‌رفتند. اعداد مختلط نیز ماهیت مشابهی دارند و روش جدیدی برای تفکر محسوب می‌شوند. هم صفر و هم اعداد مختلط باعث می‌شوند که ریاضیات بسیار آسان‌تر شود. اگر سیستم عددی عجیب جدید را هرگز نمی‌پذیرفتیم، همچنان مشغول محاسبه با انگشت‌های خود بودیم.

دلیل این تأکید روی مقایسه اعداد مختلط با اعداد منفی، صفر و غیره این است که افراد همواره به راحتی فکر می‌کنند که اعداد مختلط، نرمال نیستند. اما باید با ذهن باز با مفاهیم جدید روبه‌رو شد. در آینده نسلی خواهد آمد که این عجیب بودن اعداد مختلط برای ما برایشان مضحک خواهد بود... شاید تا 2000 سال دیگر!

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• اعداد مختلط – به زبان ساده
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی 
• اعداد حقیقی — به زبان ساده
• اعداد اصلی، ترتیبی و اسمی – مفاهیم و تعاریف به زبان ساده
• عدد پی چگونه کشف شد؟ — ریاضیات به زبان ساده

==