توابع هذلولوی یا هیپربولیک — از صفر تا صد

اگر در زمینه علوم فیزیک، مهندسی و ریاضیات کار کنید، با مدلهای زیادی سروکار خواهید داشت و برای برخی از مسائل مدلسازی، به توابع هذلولوی نیاز دارید. توابع هذلولوی نامهایی شبیه توابع مثلثاتی دارند، اما برحسب توابع نمایی تعریف میشوند. در این آموزش «توابع هذلولوی» (Hyperbolic functions) یا هیپربولیک را معرفی کرده و جنبههای مختلف آنها را بررسی میکنیم. همچنین درباره برخی فرمولهای این توابع بحث خواهیم کرد.
توابع $$\sinh x$$ و $$\cosh x$$ با استفاده از تابع نمایی $$e^x$$ تعریف میشوند. میدانیم توابع مثلثاتی با دایره سروکار دارند و بر اساس آن تعریف میشوند. اما، توابع هذلولوی با هذلولی ارتباط دارند. به همین دلیل است که آنها را توابع هذلولوی یا هیپیربولیک مینامند. علاوه بر مدلسازی، این توابع در حل برخی معادلات با مشتقات جزئی نیز کاربرد دارند.
زنجیر شکل زیر را در نظر بگیرید که دو انتهای آن به مکانهای ثابتی متصل شده و تحت نیروی گرانش رها شده است. شکل زنجیر بهصورت طبیعی یک منحنی کسینوس هیپربولیک را تشکیل میدهد.

اگر به اطرافتان دقت کنید، سازههایی را خواهید یافت که شبیه توابع هذلولوی هستند. شکل زیر مشابه تابع کسینوس هیپربولیک است.

توابع هذلولوی
شش تابع مثلثاتی هیپربولیکی وجود دارد که بهصورت زیر تعریف میشوند.

نمودار توابع بالا در شکل زیر آورده شده است.
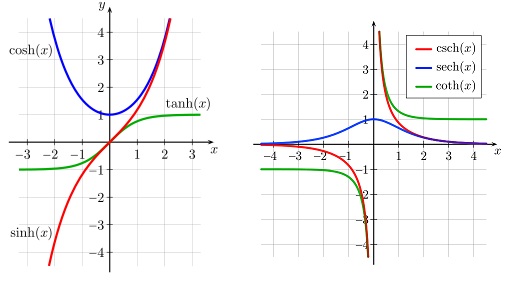
ارتباط با معادله اویلر
یکی از مشخصههای اساسی که سبب میشود توابل هذلولوی مشابه توابع مثلثاتی باشند، فرمول اویلر است:
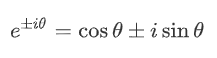
با استفاده از معادله اویلر میتوان معادلات $$\sin \theta$$ و $$\cos \theta$$ را بهصورت زیر بیان کرد:
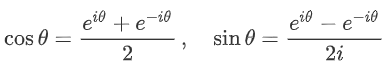
توابع سینوس هیپربولیک و کسینوس هیپربولیک نیز بهشکل زیر بیان میشوند:
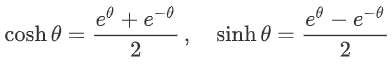
این روابط کموبیش مشابه یکدیگرند، اما قسمتهای موهومی در توابع هذلولوی وجود ندارد. در ادامه خواهیم دید که توابع هذلولوی با هم روابطی دارند که مشابه توابع مثلثاتی است.
مثال
عبارتهای $$e^\theta$$ و $$e^{- \theta}$$ را بر حسب توابع $$\sinh \theta$$ و $$\cosh \theta$$ بنویسید.
حل: با جمع دو تابع $$\sinh \theta$$ و $$\cosh \theta$$، داریم:
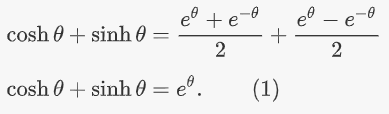
تفاضل دو تابع $$\sinh \theta$$ و $$\cosh \theta$$ نیز منجر به رابطه زیر میشود:
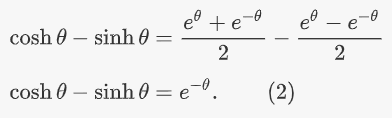
در نهایت، ترکیب معادلات (۱) و (۲)، رابطه زیر را نتیجه میدهد:
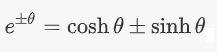
که معادل فرمول اویلر برای توابع هذلولوی است.
ارتباط با معادلات دایره واحد
معادلات پارامتری دایره واحد، بهصورت زیر است:
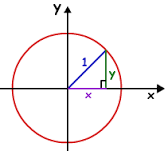
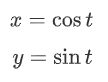
بهطریق مشابه، معلادلات پارامتری یک هذلولی واحد را میتوان بهشکل زیر نوشت:
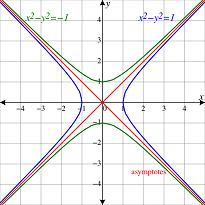
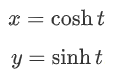
مثال
نشان دهید توابع کسینوس هیپربولیک و سینوس هیپربولیک، معادله یک هذلولی ($$x^2-y^2=1$$) را تشکیل میدهند.
حل: با توابع هذلولی زیر شروع میکنیم:
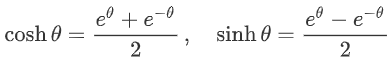
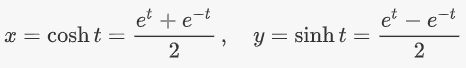
بنابراین، داریم:
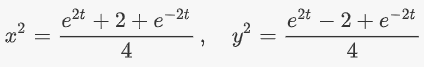
با تفریق دو عبارت از یکدیگر، رابطه داده شده اثبات میشود:
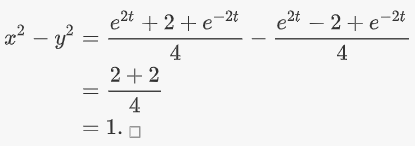
برخی روابط مفید
تعدادی از روابط مربوط به توابع هذلولوی که ممکن است در حل مسائل، به آنها نیاز داشته باشم، بهصورت زیر هستند:
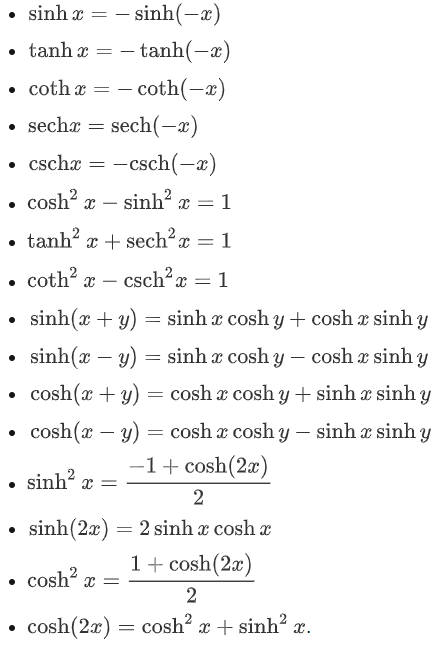
مثال
نشان دهید $$\cosh (2x)=\cosh ^2 x+ \sinh ^2 x$$.

حل: از تعریف توابع سینوس هیپربولیک و کسینوس هیپربولیک استفاده میکنیم:
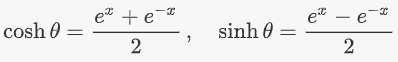
بنابراین:
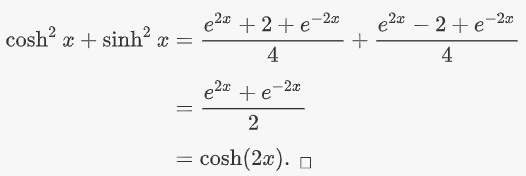
مشتق توابع هذلولوی
از آنجایی که توابع هیپربولیک، بر اساس توابع نمایی تعریف میشوند، محاسبه مشتق آنها ساده است. همانطور که میدانیم، مشتق تابع نمایی بهصورت زیر تعریف میشود:
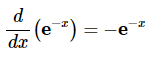
با استفاده از این فرمول، میتوانیم مشتق تابع سینوس هیپربولیک را بهدست آوریم:

محاسبه مشتق سایر توابع هذلولوی، مشابه روندی است که برای سینوس هیپربولیک انجام شد. با انجام محاسبات مربوطه، میتوان مشتق توابع هذلولی را بهشکل زیر بیان کرد:

مثال
مشتق توابع زیر را محاسبه کنید.
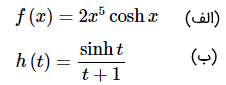
حل:
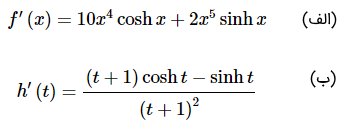











انتگرال هاشو هم میزاشتید تکمیل بود ولی بازم ممنون
عالی خیلی
بسیار عالی، متشکرم
عالی خیلی خوب بیان شده بود
عالی بود
سلام ایا این توابع در صنعت هوا فضا هم کاربرد دارند
من محور مثلثات رو خیلی خوب یار گرفتم از طریق فرادرس تابع هیپربولیک رو یک خورده یاد گرفتم ولی فککنم با توجه به سن کم هنوز (۱۳سال)یک تورده درکش برامسخته
عالی بود ولی کاش میگفتین این فورمول ها از کجا اومدن ولی در کل کار راه بنداز و به درد بخور بود ممنون
فوق العاده مثل همیشع
سلام. لطف میکنید بفرمایید خود زاویهای که مقادیر هایپربولیک آن را میخواهیم محاسبه کنیم، روی هذلولی متساویالقطرین واحد، چگونه نمایش داده میشود؟
چون برای نسبتهای مثلثاتی معمولی، زاویهٔ مورد نظر بر روی دایرهٔ مثلثاتی، و اینکه انتهای زاویه در کدام ربع دایره واقع میشود را بهراحتی میتوان نشان داد.
بسیار ممنونم.
عالی دمتون گرم
سلام ممنون یه سوال داشتم میشه بگید که اسم هیپربولیک از کجا اومده به غیر از هزلولی منظورم ریشش هسته به چیزی به غیر از هزلولی میرسه؟
بسیار علی 🙂
استفاده کردم خیلی ممنون از مطلب خوب و خلاصه تون
احسنت.
بسیار عالی
مرسی از مطالب خوبتون،مرسی از بیان واضح و خوبتون??????