قبلاً در مجموعه آموزشهای ریاضیات مجله فرادرس، مفاهیم مربوط به مشتق را بیان کردیم. در این آموزشها، مباحثی مانند مشتق ضمنی ، مشتق جزئی ، مشتق زنجیرهای و نقطه عطف تابع بحث شد. در این آموزش، مشتق مراتب بالاتر را برای توابع صریح، ضمنی و پارامتری معرفی میکنیم. همچنین، مثالهای مختلفی را برای آشنایی با حالتهای مختلف ارائه خواهیم کرد.
مشتقات مراتب بالاتر یک تابع صریح
فرض کنید تابع y = f ( x ) y = f\left( x \right) y = f ( x ) f ’ ( x ) f’\left( x \right) f ’ ( x ) ( a , b ) \left( {a,b} \right) ( a , b ) f ’ ( x ) f’\left( x \right) f ’ ( x ) f ’ ( x ) f’\left( x \right) f ’ ( x ) f ( x ) f(x) f ( x )
f ′ ′ = ( f ′ ) ′ = ( d y d x ) ′ = d d x ( d y d x ) = d 2 y d x 2 . \large {f^{\prime\prime} = \left({f^\prime}\right)^\prime = {\left( {\frac{{dy}}{{dx}}} \right)^\prime } }={ \frac{d}{{dx}}\left( {\frac{{dy}}{{dx}}} \right) }={ \frac{{{d^2}y}}{{d{x^2}}}.} f ′′ = ( f ′ ) ′ = ( d x d y ) ′ = d x d ( d x d y ) = d x 2 d 2 y .
بهطور مشابه، اگر f ′ ′ f^{\prime\prime} f ′′ f ( x ) f(x) f ( x )
f ′ ′ ′ = d 3 y d x 3 = y ′ ′ ′ . \large {f^{\prime\prime\prime} = \frac{{{d^3}y}}{{d{x^3}}} }={ y^{\prime\prime\prime}.} f ′′′ = d x 3 d 3 y = y ′′′ .
مشتقات مراتب بالاتر (اگر وجود داشته باشند)، به صورت زیر تعریف میشوند:
f ( 4 ) = d 4 y d x 4 = y ( 4 ) = ( f ( 3 ) ) ′ , … , f ( n ) = d n y d x n = y ( n ) = ( f ( n – 1 ) ) ′ . \large {{{f^{\left( 4 \right)}} = \frac{{{d^4}y}}{{d{x^4}}} }={ {y^{\left( 4 \right)}} = {\left( {{f^{\left( 3 \right)}}} \right)^\prime },} \ldots ,}\kern-0.3pt
{{f^{\left( n \right)}} = \frac{{{d^n}y}}{{d{x^n}}} = {y^{\left( n \right)}} }={ {\left( {{f^{\left( {n – 1} \right)}}} \right)^\prime }.} f ( 4 ) = d x 4 d 4 y = y ( 4 ) = ( f ( 3 ) ) ′ , … , f ( n ) = d x n d n y = y ( n ) = ( f ( n –1 ) ) ′ .
بنابراین، مشتق مرتبه n n n n n n n n n
y ( n ) = ( y ( n – 1 ) ) ′ . \large {y^{\left( n \right)}} = {\left( {{y^{\left( {n – 1} \right)}}} \right)^\prime }. y ( n ) = ( y ( n –1 ) ) ′ .
در برخی موارد میتوان یک فرمول کلی برای مشتق مرتبه n n n
روابط خطی زیر، برای پیدا کردن فرمول مشتقات مراتب بالاتر مفید هستند:
( u + v ) ( n ) = u ( n ) + v ( n ) , ( C u ) ( n ) = C u ( n ) \large {{\left( {u + v} \right)^{\left( n \right)}} = {u^{\left( n \right)}} + {v^{\left( n \right)}},\;\;\;}\kern-0.3pt
{{\left( {Cu} \right)^{\left( n \right)}} = C{u^{\left( n \right)}}\;\;} ( u + v ) ( n ) = u ( n ) + v ( n ) , ( C u ) ( n ) = C u ( n )
که در آن، C C C
مشتقات مراتب بالاتر یک تابع ضمنی
مشتق مرتبه n n n n n n F ( x , y ) = 0 F\left( {x,y} \right) = 0 F ( x , y ) = 0 x x x y y y
y ’ = f 1 ( x , y ) , y ′ ′ = f 2 ( x , y ) , … , y ( n ) = f n ( x , y ) . \large {y’ = {f_1}\left( {x,y} \right),\;\;\;}\kern-0.3pt
{y^{\prime\prime} = {f_2}\left( {x,y} \right), \ldots,\;\;\;}\kern-0.3pt
{{y^{\left( n \right)}} = {f_n}\left( {x,y} \right).} y ’ = f 1 ( x , y ) , y ′′ = f 2 ( x , y ) , … , y ( n ) = f n ( x , y ) .
مشتق مراتب بالاتر یک تابع پارامتری
تابع y = f ( x ) y = f\left( x \right) y = f ( x )
{ x = x ( t ) y = y ( t ) . \large\left\{
\begin{aligned}
x &= x\left( t \right) \\
y &= y\left( t \right)
\end{aligned}
\right.. ⎩ ⎨ ⎧ x y = x ( t ) = y ( t ) .
مشتق این تابع، برابر است با:
y ’ = y ’ x = y ’ t x ’ t . \large y’ = {y’_x} = \frac{{{y’_t}}}{{{x’_t}}}. y ’ = y ’ x = x ’ t y ’ t .
اگر یک بار دیگر نسبت به x x x
y ′ ′ = y x x ′ ′ = ( y ’ x ) ’ t x ’ t . \large y^{\prime\prime} = {y^{\prime\prime}_{xx}} = \frac{{{\left( {{y’_x}} \right)}’_t}}{{{x’_t}}}. y ′′ = y xx ′′ = x ’ t ( y ’ x ) ’ t .
بهطریق مشابه میتوان مشتقات مرتبه سوم و بالاتر را بهصورت زیر نوشت:
y ′ ′ ′ = y x x x ′ ′ ′ = ( y x x ′ ′ ) ’ t x ’ t , … , y ( n ) = y x x … x ⏟ n ( n ) = ( y x x … x ⏟ n – 1 ( n – 1 ) ) ’ t x ’ t . \large {{y^{ \prime \prime \prime} = {y^{ \prime \prime \prime}_{xxx}} = \frac{{{{ \left( {{y^{\prime\prime}_{xx}}} \right)}’_t}}}{{{x’_t}}}, \ldots,}\;\;}\kern0pt
{{{y^{ \left( n \right)}} = y_{ \underbrace {xx \ldots x}_n}^{\left( n \right)} }={ \frac{{{{\left( {y_{\underbrace {xx \ldots x}_{n – 1}}^{\left( {n – 1} \right)}} \right)}’_t}}}{{{x’_t}}}.}} y ′′′ = y xxx ′′′ = x ’ t ( y xx ′′ ) ’ t , … , y ( n ) = y n xx … x ( n ) = x ’ t ( y n –1 xx … x ( n –1 ) ) ’ t .
در صورت علاقه به یادگیری روشهای تعیین مشتق توابع مختلف، مطالعه مطلب «فرمولهای مشتق مهم + سوال با جواب و دانلود PDF » را به شما پیشنهاد میکنیم.
مثالها
در ادامه، چند مثال حلشده را بررسی میکنیم که نحوه محاسبه مشتقات مراتب بالاتر را بهخوبی نشان میدهند.
مثال ۱
اگر y = x ln x y = x\ln x y = x ln x y ′ ′ y^{\prime\prime} y ′′
حل: مشتق اول را با استفاده از قاعده مشتق ضرب دو تابع ، داریم:
y ’ = ( x ln x ) ’ = x ’ ⋅ ln x + x ⋅ ( ln x ) ′ = 1 ⋅ ln x + x ⋅ 1 x = ln x + 1. \large {y’ = \left( {x\ln x} \right)’ }
={ x’ \cdot \ln x + x \cdot {\left( {\ln x} \right)^\prime } }
={ 1 \cdot \ln x + x \cdot \frac{1}{x} = \ln x + 1.} y ’ = ( x ln x ) ’ = x ’ ⋅ ln x + x ⋅ ( ln x ) ′ = 1 ⋅ ln x + x ⋅ x 1 = ln x + 1.
اکنون میتوانیم مشتق مرتبه دوم را محاسبه کنیم:
y ′ ′ = ( ln x + 1 ) ′ = 1 x + 0 = 1 x . \large {y^{\prime\prime} = {\left( {\ln x + 1} \right)^\prime } }
= {\frac{1}{x} + 0 = \frac{1}{x}.} y ′′ = ( ln x + 1 ) ′ = x 1 + 0 = x 1 .
مثال ۲
مشتق دوم تابع y = x + 1 4 y = \sqrt[\large 4\normalsize]{{x + 1}} y = 4 x + 1
حل: ابتدا، مشتق اول را مینویسیم:
با یک بار دیگر مشتق گرفتن از تابع، داریم:
مثال ۳
عبارت y ′ ′ y^{\prime\prime} y ′′ y 2 = 4 x {y^2} = 4x y 2 = 4 x
حل: با استفاده از مشتقگیری ضمنی، داریم:
2 y y ’ = 4 , ⇒ y y ’ = 2. \large {2yy’ = 4,\;\; }\Rightarrow {yy’ = 2.} 2 yy ’ = 4 , ⇒ yy ’ = 2.
با مشتقگیری مجدد و استفاده از قاعده مشتق ضرب دو تابع، میتوان نوشت:
y ’ y ’ + y y ′ ′ = 0. \large y’y’ + yy^{\prime\prime} = 0. y ’ y ’ + y y ′′ = 0.
اگر دو طرف معادله اخیر را در y 2 {y^2} y 2
y 2 ( y ’ ) 2 + y 3 y ′ ′ = 0. \large {y^2}{\left( {y’} \right)^2} + {y^3}y^{\prime\prime} = 0. y 2 ( y ’ ) 2 + y 3 y ′′ = 0.
از آنجایی که y y ’ = 2 yy’ = 2 yy ’ = 2 ( y y ’ ) 2 = 4 {\left( {yy’} \right)^2} = 4 ( yy ’ ) 2 = 4
4 + y 3 y ′ ′ = 0. \large 4 + {y^3}y^{\prime\prime} = 0. 4 + y 3 y ′′ = 0.
در نتیجه:
y ′ ′ = – 4 y 3 . \large y^{\prime\prime} = – \frac{4}{{{y^3}}}. y ′′ = – y 3 4 .
مثال ۴
تابع y = ( 2 x + 1 ) 3 ( x – 1 ) y = {\left( {2x + 1} \right)^3}\left( {x – 1} \right) y = ( 2 x + 1 ) 3 ( x –1 )
حل: ابتدا تابع را بهصورت یک چندجملهای مینویسیم:
اکنون، مشتقات مرتبه اول تا پنجم را محاسبه میکنیم:
y ’ = ( 8 x 4 + 4 x 3 – 6 x 2 – 5 x – 1 ) ′ = 32 x 3 + 12 x 2 – 12 x – 5 , \large {y’ = {\left( {8{x^4} + 4{x^3} – 6{x^2} – 5x – 1} \right)^\prime } }={ 32{x^3} + 12{x^2} – 12x – 5,} y ’ = ( 8 x 4 + 4 x 3 –6 x 2 –5 x –1 ) ′ = 32 x 3 + 12 x 2 –12 x –5 ,
y ′ ′ = ( y ’ ) ′ = ( 32 x 3 + 12 x 2 – 12 x – 5 ) ′ = 96 x 2 + 24 x – 12 , \large {y^{\prime\prime} = {\left( {y’} \right)^\prime } }={ {\left( {32{x^3} + 12{x^2} – 12x – 5} \right)^\prime } }={ 96{x^2} + 24x – 12,} y ′′ = ( y ’ ) ′ = ( 32 x 3 + 12 x 2 –12 x –5 ) ′ = 96 x 2 + 24 x –12 ,
y ′ ′ ′ = ( y ′ ′ ) ′ = ( 96 x 2 + 24 x – 12 ) ′ = 192 x + 24 , \large {y^{\prime\prime\prime} = {\left( {y^{\prime\prime}} \right)^\prime } }={ {\left( {96{x^2} + 24x – 12} \right)^\prime } }={ 192x + 24,} y ′′′ = ( y ′′ ) ′ = ( 96 x 2 + 24 x –12 ) ′ = 192 x + 24 ,
y ( 4 ) = ( y ′ ′ ′ ) ′ = ( 192 x + 24 ) ′ = 192 , \large {{y^{\left( 4 \right)}} = {\left( {y^{\prime\prime\prime}} \right)^\prime } }={ {\left( {192x + 24} \right)^\prime } }={ 192,} y ( 4 ) = ( y ′′′ ) ′ = ( 192 x + 24 ) ′ = 192 ,
y ( 5 ) = ( y ( 4 ) ) ′ = ( 192 ) ′ = 0. \large {{y^{\left( 5 \right)}} = {\left( {{y^{\left( 4 \right)}}} \right)^\prime } }={ {\left( {192} \right)^\prime } }={ 0.} y ( 5 ) = ( y ( 4 ) ) ′ = ( 192 ) ′ = 0.
مثال ۵
مشتق مرتبه n n n لگاریتم طبیعی y = ln x y = \ln x y = ln x
حل: ابتدا چند مشتق اول را محاسبه میکنیم:
y ’ = ( ln x ) ′ = 1 x , \large {y’ = {\left( {\ln x} \right)^\prime } = \frac{1}{x},} y ’ = ( ln x ) ′ = x 1 ,
y ′ ′ = ( y ’ ) ′ = ( 1 x ) ′ = ( x – 1 ) ′ = – x – 2 = – 1 x 2 , \large {y^{\prime\prime} = {\left( {y’} \right)^\prime } = {\left( {\frac{1}{x}} \right)^\prime } }={ {\left( {{x^{ – 1}}} \right)^\prime } }={ – {x^{ – 2}} }={ – \frac{1}{{{x^2}}},} y ′′ = ( y ’ ) ′ = ( x 1 ) ′ = ( x –1 ) ′ = – x –2 = – x 2 1 ,
y ′ ′ ′ = ( y ′ ′ ) ′ = ( – 1 x 2 ) ′ = 2 x – 3 = 2 x 3 , \large {y^{\prime\prime\prime} = {\left( {y^{\prime\prime}} \right)^\prime } }={ {\left( { – \frac{1}{{{x^2}}}} \right)^\prime } }={ 2{x^{ – 3}} }={ \frac{2}{{{x^3}}},} y ′′′ = ( y ′′ ) ′ = ( – x 2 1 ) ′ = 2 x –3 = x 3 2 ,
y ( 4 ) = ( y ′ ′ ′ ) ′ = ( 2 x 3 ) ′ = – 6 x – 4 = – 6 x 4 , \large {{y^{\left( 4 \right)}} = {\left( {y^{\prime\prime\prime}} \right)^\prime } }={ {\left( {\frac{2}{{{x^3}}}} \right)^\prime } }={ – 6{x^{ – 4}} }={ – \frac{6}{{{x^4}}},} y ( 4 ) = ( y ′′′ ) ′ = ( x 3 2 ) ′ = –6 x –4 = – x 4 6 ,
y ( 5 ) = ( y ( 4 ) ) ′ = ( – 6 x 4 ) ′ = 24 x – 5 = 24 x 5 . \large {{y^{\left( 5 \right)}} = {\left( {{y^{\left( 4 \right)}}} \right)^\prime } }={ {\left( { – \frac{6}{{{x^4}}}} \right)^\prime } }={ 24{x^{ – 5}} }={ \frac{{24}}{{{x^5}}}.} y ( 5 ) = ( y ( 4 ) ) ′ = ( – x 4 6 ) ′ = 24 x –5 = x 5 24 .
همانطور که میبینیم، حاصل مشتقات بالا، از الگوریتم خاصی پیروی میکنند که میتوان آن را برای مرتبه دلخواه n n n
y ( n ) = ( – 1 ) n – 1 ( n – 1 ) ! x n . \large {y^{\left( n \right)}} = \frac{{{{\left( { – 1} \right)}^{n – 1}}\left( {n – 1} \right)!}}{{{x^n}}}. y ( n ) = x n ( –1 ) n –1 ( n –1 ) ! .
اثبات دقیق فرمول بالا را میتوان با استقرای ریاضی بیان کرد.
مثال ۶
همه مشتقات تابع سینوس را محاسبه کنید.
حل: ابتدا چند مشتق اول این تابع را مینویسیم:
y ’ = ( sin x ) ′ = cos x = sin ( x + π 2 ) , \large {y’ = {\left( {\sin x} \right)^\prime } = \cos x }={ \sin \left( {x + \frac{\pi }{2}} \right),} y ’ = ( sin x ) ′ = cos x = sin ( x + 2 π ) ,
y ′ ′ = ( cos x ) ′ = – sin x = sin ( x + 2 ⋅ π 2 ) , \large {y^{\prime\prime} = {\left( {\cos x} \right)^\prime } = – \sin x }={ \sin \left( {x + 2 \cdot \frac{\pi }{2}} \right),} y ′′ = ( cos x ) ′ = – sin x = sin ( x + 2 ⋅ 2 π ) ,
y ′ ′ ′ = ( – sin x ) ′ = – cos x = sin ( x + 3 ⋅ π 2 ) , \large {y^{\prime\prime\prime} = {\left( { – \sin x} \right)^\prime } = – \cos x }={ \sin \left( {x + 3 \cdot \frac{\pi }{2}} \right),} y ′′′ = ( – sin x ) ′ = – cos x = sin ( x + 3 ⋅ 2 π ) ,
y I V = ( – cos x ) ′ = sin x = sin ( x + 4 ⋅ π 2 ) . \large {{y^{IV}} = {\left( { – \cos x} \right)^\prime } = \sin x }={ \sin \left( {x + 4 \cdot \frac{\pi }{2}} \right).} y I V = ( – cos x ) ′ = sin x = sin ( x + 4 ⋅ 2 π ) .
واضح است که مشتق مرتبه n n n
y ( n ) = ( sin x ) ( n ) = sin ( x + n π 2 ) . \large {{y^{\left( n \right)}} = {\left( {\sin x} \right)^{\left( n \right)}} }={ \sin \left( {x + \frac{{n\pi }}{2}} \right).} y ( n ) = ( sin x ) ( n ) = sin ( x + 2 nπ ) .
مثال ۷
همه مشتقات تابع کسینوس را محاسبه کنید.
حل: مانند مثال ۶، ابتدا چند مشتق اول این تابع را مینویسیم:
y ’ = ( cos x ) ′ = – sin x = cos ( x + π 2 ) , \large {y’ = {\left( {\cos x} \right)^\prime } = – \sin x }={ \cos \left( {x + \frac{\pi }{2}} \right),} y ’ = ( cos x ) ′ = – sin x = cos ( x + 2 π ) ,
y ′ ′ = ( – sin x ) ′ = – cos x = cos ( x + 2 ⋅ π 2 ) , \large {y^{\prime\prime} = {\left( { – \sin x} \right)^\prime } = – \cos x }={ \cos \left( {x + 2 \cdot \frac{\pi }{2}} \right),} y ′′ = ( – sin x ) ′ = – cos x = cos ( x + 2 ⋅ 2 π ) ,
y ′ ′ ′ = ( – cos x ) ′ = sin x = cos ( x + 3 ⋅ π 2 ) , \large {y^{\prime\prime\prime} = {\left( { – \cos x} \right)^\prime } = \sin x }={ \cos \left( {x + 3 \cdot \frac{\pi }{2}} \right),} y ′′′ = ( – cos x ) ′ = sin x = cos ( x + 3 ⋅ 2 π ) ,
y I V = ( sin x ) ′ = cos x = cos ( x + 4 ⋅ π 2 ) . \large {{y^{IV}} = {\left( {\sin x} \right)^\prime } = \cos x }={ \cos \left( {x + 4 \cdot \frac{\pi }{2}} \right).} y I V = ( sin x ) ′ = cos x = cos ( x + 4 ⋅ 2 π ) .
از عبارات بالا مشخص است که مشتق پنجم با مشتق اول، مشتق ششم با مشتق دوم و... مشابه هستند. بنابراین، مشتق مرتبه n n n
y ( n ) = ( cos x ) ( n ) = cos ( x + n π 2 ) . \large {{y^{\left( n \right)}} = {\left( {\cos x} \right)^{\left( n \right)}} }={ \cos \left( {x + \frac{{n\pi }}{2}} \right).} y ( n ) = ( cos x ) ( n ) = cos ( x + 2 nπ ) .
مثال ۸
مشتق مرتبه n n n y = 1 x y = {\large\frac{1}{x}\normalsize} y = x 1
حل: ابتدا چند مشتق اول را محاسبه میکنیم تا الگوریتم کلی مشتقات مرتبه بالاتر مشخص شود:
y ’ = ( 1 x ) ′ = – 1 x 2 , \large {y’ = {\left( {\frac{1}{x}} \right)^\prime } = – \frac{1}{{{x^2}}},} y ’ = ( x 1 ) ′ = – x 2 1 ,
y ′ ′ = ( – 1 x 2 ) ′ = – 1 ⋅ ( x – 2 ) ′ = − 1 ⋅ ( – 2 ) ⋅ x – 3 = ( – 1 ) 2 ⋅ 2 x 3 , \large {{y^{\prime\prime} = {\left( { – \frac{1}{{{x^2}}}} \right)^\prime } }={ – 1 \cdot {\left( {{x^{ – 2}}} \right)^\prime }}
= {- 1 \cdot \left( { – 2} \right) \cdot {x^{ – 3}} }={ \frac{{{{\left( { – 1} \right)}^2} \cdot 2}}{{{x^3}}},}} y ′′ = ( – x 2 1 ) ′ = –1 ⋅ ( x –2 ) ′ = − 1 ⋅ ( –2 ) ⋅ x –3 = x 3 ( –1 ) 2 ⋅ 2 ,
y ′ ′ ′ = ( ( – 1 ) 2 ⋅ 2 x 3 ) ′ = ( – 1 ) 2 ⋅ 2 ⋅ ( x – 3 ) ′ = ( – 1 ) 3 ⋅ 2 ⋅ 3 ⋅ x – 4 = ( – 1 ) 2 ⋅ 2 ⋅ 3 x 4 , \large {{y^{\prime\prime\prime} = {\left( {\frac{{{{\left( { – 1} \right)}^2} \cdot 2}}{{{x^3}}}} \right)^\prime } }={ {\left( { – 1} \right)^2} \cdot 2 \cdot {\left( {{x^{ – 3}}} \right)^\prime } }
= {{\left( { – 1} \right)^3} \cdot 2 \cdot 3 \cdot {x^{ – 4}} }={ \frac{{{{\left( { – 1} \right)}^2} \cdot 2 \cdot 3}}{{{x^4}}},}} y ′′′ = ( x 3 ( –1 ) 2 ⋅ 2 ) ′ = ( –1 ) 2 ⋅ 2 ⋅ ( x –3 ) ′ = ( –1 ) 3 ⋅ 2 ⋅ 3 ⋅ x –4 = x 4 ( –1 ) 2 ⋅ 2 ⋅ 3 ,
y I V = ( ( – 1 ) 2 ⋅ 2 ⋅ 3 x 4 ) ′ = ( – 1 ) 3 ⋅ 2 ⋅ 3 ⋅ ( x – 4 ) ′ = ( – 1 ) 4 ⋅ 4 ! ⋅ x – 5 = ( – 1 ) 4 4 ! x 5 . \large {{{y^{IV}} = {\left( {\frac{{{{\left( { – 1} \right)}^2} \cdot 2 \cdot 3}}{{{x^4}}}} \right)^\prime } = {\left( { – 1} \right)^3} \cdot 2 \cdot 3 \cdot {\left( {{x^{ – 4}}} \right)^\prime } }
= {{\left( { – 1} \right)^4} \cdot 4! \cdot {x^{ – 5}} }={ \frac{{{{\left( { – 1} \right)}^4}4!}}{{{x^5}}}.}} y I V = ( x 4 ( –1 ) 2 ⋅ 2 ⋅ 3 ) ′ = ( –1 ) 3 ⋅ 2 ⋅ 3 ⋅ ( x –4 ) ′ = ( –1 ) 4 ⋅ 4 ! ⋅ x –5 = x 5 ( –1 ) 4 4 ! .
همین چهار مشتق، برای حدس زدن رابطه مشتق n n n
y ( n ) = ( – 1 ) n n ! x n + 1 . \large {{y^{\left( n \right)}} }={ \frac{{{{\left( { – 1} \right)}^n}n!}}{{{x^{n + 1}}}}.} y ( n ) = x n + 1 ( –1 ) n n ! .
مثال ۹
مشتق دوم تابع زیر را حساب کنید:
y = arcsin x 2 – 1 x 2 + 1 . \large y = \arcsin {\large\frac{{{x^2} – 1}}{{{x^2} + 1}}\normalsize}. y = arcsin x 2 + 1 x 2 –1 .
حل: با مشتقگیری از این تابع، بهعنوان یک تابع ترکیبی، داریم:
$$\large \require{cancel}<br />
{y = {\left( {\arcsin \frac{{{x^2} – 1}}{{{x^2} + 1}}} \right)^\prime } }<br />
= {\frac{1}{{\sqrt {1 – {{\left( {\frac{{{x^2} – 1}}{{{x^2} + 1}}} \right)}^2}} }} \cdot}\kern0pt{ {\left( {\frac{{{x^2} – 1}}{{{x^2} + 1}}} \right)^\prime } } \\ \large<br />
= {\frac{1}{{\sqrt {\frac{{{{\left( {{x^2} + 1} \right)}^2} – {{\left( {{x^2} – 1} \right)}^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}}} }} \cdot}\kern0pt{ \frac{{2x \cdot \left( {{x^2} + 1} \right) – \left( {{x^2} – 1} \right) \cdot 2x}}{{{{\left( {{x^2} + 1} \right)}^2}}} } \\ \large<br />
= {\frac{{{4x}}}{{\sqrt {{4{x^2}}} \left( {{x^2} + 1} \right)}} }<br />
= {\frac{{4x}}{{2\left| x \right|\left( {{x^2} + 1} \right)}} }<br />
= {\frac{{2x}}{{\left| x \right|\left( {{x^2} + 1} \right)}}.}$$
در رابطه اخیر، ∣ x ∣ {\left| x \right|} ∣ x ∣ x sign x x\,\text{sign}\,x x sign x
sign x = { – 1 , if x < 0 0 , if x = 0 + 1 , if x > 0 . \large \text{sign}\,x =
\begin{cases}
– 1, & \text{if}\;\;x \lt 0 \\
0, & \text{if} \;\;x = 0 \\
+ 1, & \text{if} \;\;x \gt 0
\end{cases}
. sign x = ⎩ ⎨ ⎧ –1 , 0 , + 1 , if x < 0 if x = 0 if x > 0 .
در نتیجه، داریم:
y ’ = 2 x ∣ x ∣ ( x 2 + 1 ) = 2 x x sign x ( x 2 + 1 ) = 2 sign x x 2 + 1 . \large {y’ = \frac{{2x}}{{\left| x \right|\left( {{x^2} + 1} \right)}} }
= {\frac{{2\cancel{x}}}{{\cancel{x} \,\text{sign}\,x\left( {{x^2} + 1} \right)}} }
= {\frac{{2\,\text{sign}\,x}}{{{x^2} + 1}}.} y ’ = ∣ x ∣ ( x 2 + 1 ) 2 x = x sign x ( x 2 + 1 ) 2 x = x 2 + 1 2 sign x .
اکنون مشتق دوم را محاسبه میکنیم:
y ′ ′ = ( 2 sign x x 2 + 1 ) ′ = 0 ⋅ ( x 2 + 1 ) – 2 sign x ⋅ 2 x ( x 2 + 1 ) 2 = – 4 x sign x ( x 2 + 1 ) 2 . \large {y^{\prime\prime} = {\left( {\frac{{2\,\text{sign}\,x}}{{{x^2} + 1}}} \right)^\prime } }
= {\frac{{0 \cdot \left( {{x^2} + 1} \right) – 2\,\text{sign}\,x \cdot 2x}}{{{{\left( {{x^2} + 1} \right)}^2}}} }
= { – \frac{{4x\,\text{sign}\,x}}{{{{\left( {{x^2} + 1} \right)}^2}}}.} y ′′ = ( x 2 + 1 2 sign x ) ′ = ( x 2 + 1 ) 2 0 ⋅ ( x 2 + 1 ) –2 sign x ⋅ 2 x = – ( x 2 + 1 ) 2 4 x sign x .
مثال ۱۰
مشتق دوم تابعی را بهدست آورید که بهصورت ضمنی x 2 + y 2 = R 2 {x^2} + {y^2} = {R^2} x 2 + y 2 = R 2
حل: برای یافتن مشتق اول، از هر دو سمت معادله مشتق میگیریم:
( x 2 + y 2 ) ′ = ( R 2 ) ′ , ⇒ 2 x + 2 y y ’ = 0 , ⇒ y y ’ = – x , ⇒ y ’ = – x y . \large {{\left( {{x^2} + {y^2}} \right)^\prime } = {\left( {{R^2}} \right)^\prime },\;\;}\Rightarrow
{2x + 2yy’ = 0,\;\;}\Rightarrow
{yy’ = – x,\;\;}\Rightarrow
{y’ = – \frac{x}{y}.} ( x 2 + y 2 ) ′ = ( R 2 ) ′ , ⇒ 2 x + 2 yy ’ = 0 , ⇒ yy ’ = – x , ⇒ y ’ = – y x .
اگر از عبارت بالا مشتق بگیریم، داریم:
( y ’ ) ′ = ( – x y ) ′ , ⇒ y ′ ′ = – x ’ y – x y ’ y 2 , ⇒ y ′ ′ = – y – x y ’ y 2 = x y ’– y y 2 . \large{{\left( {y’} \right)^\prime } = {\left( { – \frac{x}{y}} \right)^\prime },\;\;}\Rightarrow
{y^{\prime\prime} = – \frac{{x’y – xy’}}{{{y^2}}},\;\;} \\ \large \Rightarrow
{y^{\prime\prime} = – \frac{{y – xy’}}{{{y^2}}} = \frac{{xy’ – y}}{{{y^2}}}.} ( y ’ ) ′ = ( – y x ) ′ , ⇒ y ′′ = – y 2 x ’ y – x y ’ , ⇒ y ′′ = – y 2 y – x y ’ = y 2 x y ’– y .
با جایگذاری مشتق y ’ y’ y ’
y ′ ′ = x y ’– y y 2 = x ( – x y ) – y y 2 = – x 2 y – y y 2 = – x 2 – y 2 y 3 = – x 2 + y 2 y 3 = – R 2 y 3 . \large {y^{\prime\prime} = \frac{{xy’ – y}}{{{y^2}}} }
= {\frac{{x\left( { – \frac{x}{y}} \right) – y}}{{{y^2}}} } \\ \large
= {\frac{{ – \frac{{{x^2}}}{y} – y}}{{{y^2}}} }
= {\frac{{ – {x^2} – {y^2}}}{{{y^3}}} }
= { – \frac{{{x^2} + {y^2}}}{{{y^3}}} }
= { – \frac{{{R^2}}}{{{y^3}}}.} y ′′ = y 2 x y ’– y = y 2 x ( – y x ) – y = y 2 – y x 2 – y = y 3 – x 2 – y 2 = – y 3 x 2 + y 2 = – y 3 R 2 .
مثال ۱۱
مشتق مرتبه n n n y = 3 2 x + 1 y = {3^{2x + 1}} y = 3 2 x + 1
حل: ابتدا، چند مشتق اول این تابع را بهصورت زیر محاسبه میکنیم:
y ’ = ( 3 2 x + 1 ) ′ = 3 2 x + 1 ⋅ ln 3 ⋅ ( 2 x + 1 ) ′ = 3 2 x + 1 ⋅ 2 ln 3 , \large {y’ = {\left( {{3^{2x + 1}}} \right)^\prime } }
= {{3^{2x + 1}} \cdot \ln 3 \cdot {\left( {2x + 1} \right)^\prime } }
= {{3^{2x + 1}} \cdot 2\ln 3,} y ’ = ( 3 2 x + 1 ) ′ = 3 2 x + 1 ⋅ ln 3 ⋅ ( 2 x + 1 ) ′ = 3 2 x + 1 ⋅ 2 ln 3 ,
y ′ ′ = ( y ’ ) ′ = ( 3 2 x + 1 ⋅ 2 ln 3 ) ′ = ( 3 2 x + 1 ) ′ ⋅ 2 ln 3 = 3 2 x + 1 ⋅ 2 2 ln 2 3 , \large {y^{\prime\prime} = {\left( {y’} \right)^\prime } }
= {{\left( {{3^{2x + 1}} \cdot 2\ln 3} \right)^\prime } }
= {{\left( {{3^{2x + 1}}} \right)^\prime } \cdot 2\ln 3 }
= {{3^{2x + 1}} \cdot {2^2}{\ln ^2}3,} y ′′ = ( y ’ ) ′ = ( 3 2 x + 1 ⋅ 2 ln 3 ) ′ = ( 3 2 x + 1 ) ′ ⋅ 2 ln 3 = 3 2 x + 1 ⋅ 2 2 ln 2 3 ,
y ′ ′ ′ = ( y ′ ′ ) ′ = ( 3 2 x + 1 ⋅ 2 2 ln 2 3 ) ′ = ( 3 2 x + 1 ) ′ ⋅ 2 2 ln 2 3 = 3 2 x + 1 ⋅ 2 3 ln 3 3. \large {y^{\prime\prime\prime} = {\left( {y^{\prime\prime}} \right)^\prime } }
= {{\left( {{3^{2x + 1}} \cdot {2^2}{{\ln }^2}3} \right)^\prime } }
= {{\left( {{3^{2x + 1}}} \right)^\prime } \cdot {2^2}{\ln ^2}3 }
= {{3^{2x + 1}} \cdot {2^3}{\ln ^3}3.} y ′′′ = ( y ′′ ) ′ = ( 3 2 x + 1 ⋅ 2 2 ln 2 3 ) ′ = ( 3 2 x + 1 ) ′ ⋅ 2 2 ln 2 3 = 3 2 x + 1 ⋅ 2 3 ln 3 3.
اگر نتیجه سه مشتق اخیر را بررسی کنیم، میبینیم که میتوان مشتق مرتبه n n n
y ( n ) = ( 3 2 x + 1 ) ( n ) \large {{y^{\left( n \right)}} = {\left( {{3^{2x + 1}}} \right)^{\left( n \right)}} } y ( n ) = ( 3 2 x + 1 ) ( n )
صحت این فرمول را با استقرای ریاضی ثابت میکنیم. واضح است که فرمول اخیر، برای n = 1 n=1 n = 1 n = k n=k n = k
y ( k ) = ( 3 2 x + 1 ) ( k ) = 3 2 x + 1 ⋅ 2 k ln k 3. \large {{y^{\left( k \right)}} = {\left( {{3^{2x + 1}}} \right)^{\left( k \right)}} }
= {{3^{2x + 1}} \cdot {2^k}\,{\ln ^k}3.} y ( k ) = ( 3 2 x + 1 ) ( k ) = 3 2 x + 1 ⋅ 2 k ln k 3.
در نتیجه، برای n = k + 1 n=k+1 n = k + 1
y ( k + 1 ) = ( 3 2 x + 1 ) ( k + 1 ) = [ ( 3 2 x + 1 ) ( k ) ] ′ = ( 3 2 x + 1 ⋅ 2 k ln k 3 ) ′ = ( 3 2 x + 1 ) ′ ⋅ 2 k ln k 3 = 3 2 x + 1 ⋅ 2 k + 1 ln k + 1 3 , \large {{y^{\left( {k + 1} \right)}} = {\left( {{3^{2x + 1}}} \right)^{\left( {k + 1} \right)}} }
= {{\left[ {{{\left( {{3^{2x + 1}}} \right)}^{\left( k \right)}}} \right]^\prime } } \\ \large
= {{\left( {{3^{2x + 1}} \cdot {2^k}\,{{\ln }^k}3} \right)^\prime } }
= {{\left( {{3^{2x + 1}}} \right)^\prime } \cdot {2^k}\,{\ln ^k}3 }
= {{3^{2x + 1}} \cdot {2^{k + 1}}{\ln ^{k + 1}}3,} y ( k + 1 ) = ( 3 2 x + 1 ) ( k + 1 ) = [ ( 3 2 x + 1 ) ( k ) ] ′ = ( 3 2 x + 1 ⋅ 2 k ln k 3 ) ′ = ( 3 2 x + 1 ) ′ ⋅ 2 k ln k 3 = 3 2 x + 1 ⋅ 2 k + 1 ln k + 1 3 ,
این بدین معنی است که فرمول برای n = k + 1 n=k+1 n = k + 1 n n n
مثال ۱۲
مشتق مرتبه n n n y = x m y=x^m y = x m m m m
حل: مانند مثالهای قبل، ابتدا چند مشتق اول را حساب میکنیم:
y ’ = ( x m ) ′ = m x m – 1 , \large {y’ = {\left( {{x^m}} \right)^\prime } = m{x^{m – 1}},} y ’ = ( x m ) ′ = m x m –1 ,
y ′ ′ = ( y ’ ) ′ = ( m x m – 1 ) ′ = m ( m – 1 ) x m – 2 , \large {y^{\prime\prime} = {\left( {y’} \right)^\prime } = {\left( {m{x^{m – 1}}} \right)^\prime }
= {m\left( {m – 1} \right){x^{m – 2}},}} y ′′ = ( y ’ ) ′ = ( m x m –1 ) ′ = m ( m –1 ) x m –2 ,
y ′ ′ ′ = ( y ′ ′ ) ′ = [ m ( m – 1 ) x m – 2 ] ′ = [ m ( m – 1 ) ( m – 2 ) ] x m – 3 . \large {y^{\prime\prime\prime} = {\left( {y^{\prime\prime}} \right)^\prime } = {\left[ {m\left( {m – 1} \right){x^{m – 2}}} \right]^\prime }
= {\left[ {m\left( {m – 1} \right)\left( {m – 2} \right)} \right]{x^{m – 3}}.}} y ′′′ = ( y ′′ ) ′ = [ m ( m –1 ) x m –2 ] ′ = [ m ( m –1 ) ( m –2 ) ] x m –3 .
بنابراین، بهسادگی میتوان توصیف عمومی مشتق مرتبه n n n
y ( n ) = m ( m – 1 ) ( m – 2 ) ⋯ ( m – n + 1 ) x m – n . \large {y^{\left( n \right)}} = {m\left( {m – 1} \right)\left( {m – 2} \right) \cdots}\kern0pt{ \left( {m – n + 1} \right){x^{m – n}}.} y ( n ) = m ( m –1 ) ( m –2 ) ⋯ ( m – n + 1 ) x m – n .
صحت فرمول اخیر را با اصل استقرای ریاضی اثبات میکنیم. واضح است که فرمول مورد نظر برای n = 1 n=1 n = 1 n n n ( n + 1 ) (n+1) ( n + 1 )
y ( n + 1 ) = [ y ( n ) ] ′ = m ( m – 1 ) ( m – 2 ) ⋯ ( m – n + 1 ) ( x m – n ) ′ = m ( m – 1 ) ( m – 2 ) ⋯ ( m – n + 1 ) x m – ( n + 1 ) . \large {{y^{\left( {n + 1} \right)}} = {\left[ {{y^{\left( n \right)}}} \right]^\prime } }
= {m\left( {m – 1} \right)\left( {m – 2} \right) \cdots}\kern0pt{ \left( {m – n + 1} \right){\left( {{x^{m – n}}} \right)^\prime } }\\ \large
= {m\left( {m – 1} \right)\left( {m – 2} \right) \cdots}\kern0pt{ \left( {m – n + 1} \right){x^{m – \left( {n + 1} \right)}}.} y ( n + 1 ) = [ y ( n ) ] ′ = m ( m –1 ) ( m –2 ) ⋯ ( m – n + 1 ) ( x m – n ) ′ = m ( m –1 ) ( m –2 ) ⋯ ( m – n + 1 ) x m – ( n + 1 ) .
همانطور که میبینیم، مشتق مرتبه ( n + 1 ) (n+1) ( n + 1 ) n n n n + 1 n+1 n + 1 n n n n n n n n n m m m m m m
y ( n ) = ( x m ) ( n ) = m ! ( m – n ) ! x m – n , \large {y^{\left( n \right)}} = {\left( {{x^m}} \right)^{\left( n \right)}} = {\frac{{m!}}{{\left( {m – n} \right)!}}{x^{m – n}},} y ( n ) = ( x m ) ( n ) = ( m – n ) ! m ! x m – n ,
که در آن، n ≤ m n \le m n ≤ m n > m n \gt m n > m
مثال ۱۳
مشتق مرتبه n n n y = x y = \sqrt x y = x
حل: در اینجا، از نتیجه مثال ۱۲ استفاده میکنیم که در آن، مشتق مرتبه n n n m m m
y = x = x 1 2 ( m = 1 2 ) . {y = \sqrt x = {x^{\large\frac{1}{2}\normalsize}}\;\;}\kern0pt{\left( {m = \frac{1}{2}} \right).} y = x = x 2 1 ( m = 2 1 ) .
بنابراین، مشتق را میتوان بهصورت زیر نوشت:
y = ( x 1 2 ) ′ = 1 2 ⋅ ( 1 2 – 1 ) ( 1 2 – 2 ) ⋯ ( 1 2 – n + 1 ) x 1 2 – n = 1 2 ⋅ ( – 1 2 ) ⋅ ( – 3 2 ) ⋅ ( – 5 2 ) ⋯ [ – ( n – 3 2 ) ] x 1 2 x n = 1 2 ⋅ ( – 1 ) n – 1 [ 1 2 ⋅ 3 2 ⋅ 5 2 ⋯ 2 n – 3 2 ] x x n = 1 2 ⋅ ( – 1 ) n – 1 ⋅ 1 2 n – 1 ⋅ [ 1 ⋅ 3 ⋅ 5 ⋯ ( 2 n – 3 ) ] x x n = ( – 1 ) n – 1 [ 1 ⋅ 3 ⋅ 5 ⋯ ( 2 n – 3 ) ] x x n . \large {y = {\left( {{x^{\large\frac{1}{2}\normalsize}}} \right)^\prime } }
= {\frac{1}{2} \cdot \left( {\frac{1}{2} – 1} \right)\left( {\frac{1}{2} – 2} \right) \cdots}\kern0pt{ \left( {\frac{1}{2} – n + 1} \right){x^{\large\frac{1}{2}\normalsize – n}} } \\ \large
= {\frac{1}{2} \cdot \left( { – \frac{1}{2}} \right) \cdot}\kern0pt{ \left( { – \frac{3}{2}} \right) \cdot \left( { – \frac{5}{2}} \right) \cdots}\kern0pt{ \left[ { – \left( {n – \frac{3}{2}} \right)} \right]\frac{{{x^{\large\frac{1}{2}\normalsize}}}}{{{x^n}}} } \\ \large
= {\frac{1}{2} \cdot {\left( { – 1} \right)^{n – 1}}}\kern0pt{\left[ {\frac{1}{2} \cdot \frac{3}{2} \cdot \frac{5}{2} \cdots \frac{{2n – 3}}{2}} \right]\frac{{\sqrt x }}{{{x^n}}} } \\ \large
= {\frac{1}{2} \cdot {\left( { – 1} \right)^{n – 1}} \cdot \frac{1}{{{2^{n – 1}}}} \cdot }\kern0pt{\left[ {1 \cdot 3 \cdot 5 \cdots \left( {2n – 3} \right)} \right]\frac{{\sqrt x }}{{{x^n}}} } \\ \large
= {\frac{{{{\left( { – 1} \right)}^{n – 1}}\left[ {1 \cdot 3 \cdot 5 \cdots \left( {2n – 3} \right)} \right]\sqrt x }}{{{x^n}}}.} y = ( x 2 1 ) ′ = 2 1 ⋅ ( 2 1 –1 ) ( 2 1 –2 ) ⋯ ( 2 1 – n + 1 ) x 2 1 – n = 2 1 ⋅ ( – 2 1 ) ⋅ ( – 2 3 ) ⋅ ( – 2 5 ) ⋯ [ – ( n – 2 3 ) ] x n x 2 1 = 2 1 ⋅ ( –1 ) n –1 [ 2 1 ⋅ 2 3 ⋅ 2 5 ⋯ 2 2 n –3 ] x n x = 2 1 ⋅ ( –1 ) n –1 ⋅ 2 n –1 1 ⋅ [ 1 ⋅ 3 ⋅ 5 ⋯ ( 2 n –3 ) ] x n x = x n ( –1 ) n –1 [ 1 ⋅ 3 ⋅ 5 ⋯ ( 2 n –3 ) ] x .
برای n = 1 n=1 n = 1
y ’ = ( – 1 ) 0 ⋅ 1 ⋅ x ( 2 x ) 1 = x 2 x = 1 2 x . \large {y’ = \frac{{{{\left( { – 1} \right)}^0} \cdot 1 \cdot \sqrt x }}{{{{\left( {2x} \right)}^1}}} }
= {\frac{{\sqrt x }}{{2x}} }
= {\frac{1}{{2\sqrt x }}.} y ’ = ( 2 x ) 1 ( –1 ) 0 ⋅ 1 ⋅ x = 2 x x = 2 x 1 .
برای n ≥ 2 n \ge 2 n ≥ 2 فاکتوریل دوگانه نوشت:
1 ⋅ 3 ⋅ 5 ⋯ ( 2 n – 3 ) = ( 2 n – 3 ) ! ! \large 1 \cdot 3 \cdot 5 \cdots \left( {2n – 3} \right) = \left( {2n – 3} \right)!! 1 ⋅ 3 ⋅ 5 ⋯ ( 2 n –3 ) = ( 2 n –3 ) !!
بنابراین، برای n ≥ 2 n \ge 2 n ≥ 2 n n n
y ( n ) = 1 2 ⋅ ( – 1 ) n – 1 ⋅ 1 2 n – 1 ⋅ ( 2 n – 3 ) ! ! x x n = ( – 1 ) n – 1 ( 2 n – 3 ) ! ! x ( 2 x ) n . \large {{y^{\left( n \right)}} = \frac{1}{2} \cdot {\left( { – 1} \right)^{n – 1}} \cdot \frac{1}{{{2^{n – 1}}}} \cdot}\kern0pt{ \left( {2n – 3} \right)!!\frac{{\sqrt x }}{{{x^n}}} }
= {\frac{{{{\left( { – 1} \right)}^{n – 1}}\left( {2n – 3} \right)!!\sqrt x }}{{{{\left( {2x} \right)}^n}}}.} y ( n ) = 2 1 ⋅ ( –1 ) n –1 ⋅ 2 n –1 1 ⋅ ( 2 n –3 ) !! x n x = ( 2 x ) n ( –1 ) n –1 ( 2 n –3 ) !! x .
در نتیجه، داریم:
y ′ ′ = ( – 1 ) 1 1 ! ! x ( 2 x ) 2 = – x 4 x 2 = – 1 4 x 3 , \large {y^{\prime\prime} = \frac{{{{\left( { – 1} \right)}^1}1!!\sqrt x }}{{{{\left( {2x} \right)}^2}}} }={ – \frac{{\sqrt x }}{{4{x^2}}} }={ – \frac{1}{{4\sqrt {{x^3}} }},} y ′′ = ( 2 x ) 2 ( –1 ) 1 1 !! x = – 4 x 2 x = – 4 x 3 1 ,
y ′ ′ ′ = ( – 1 ) 2 3 ! ! x ( 2 x ) 3 = 3 x 8 x 3 = 3 8 x 5 . \large {y^{\prime\prime\prime} = \frac{{{{\left( { – 1} \right)}^2}3!!\sqrt x }}{{{{\left( {2x} \right)}^3}}} }={ \frac{{3\sqrt x }}{{8{x^3}}} }={ \frac{3}{{8\sqrt {{x^5}} }}.} y ′′′ = ( 2 x ) 3 ( –1 ) 2 3 !! x = 8 x 3 3 x = 8 x 5 3 .
مثال ۱۴
مشتق مرتبه n n n y = x 3 y = \sqrt[\large 3\normalsize]{x} y = 3 x
حل: مشتق مرتبه اول تابع، بهصورت زیر است:
y ’ = ( x 3 ) ′ = ( x 1 3 ) ′ = 1 3 x 1 3 – 1 = 1 3 x – 2 3 = 1 3 x 2 3 . \large {y’ = {\left( {\sqrt[\large 3\normalsize]{x}} \right)^\prime } = {\left( {{x^{\large\frac{1}{3}\normalsize}}} \right)^\prime } }
= {\frac{1}{3}{x^{\large\frac{1}{3}\normalsize – 1}} }
= {\frac{1}{3}{x^{ – \large\frac{2}{3}\normalsize}} }
= {\frac{1}{{3\sqrt[\large 3\normalsize]{{{x^2}}}}}.} y ’ = ( 3 x ) ′ = ( x 3 1 ) ′ = 3 1 x 3 1 –1 = 3 1 x – 3 2 = 3 3 x 2 1 .
در ادامه، از فرمول عمومی مشتق تابع توانی y = x m y=x^m y = x m
( x m ) ( n ) = m ( m – 1 ) ( m – 2 ) ⋯ ( m – n + 1 ) x m – n . \large {\left( {{x^m}} \right)^{\left( n \right)}} = {m\left( {m – 1} \right)\left( {m – 2} \right) \cdots}\kern0pt{ \left( {m – n + 1} \right){x^{m – n}}.} ( x m ) ( n ) = m ( m –1 ) ( m –2 ) ⋯ ( m – n + 1 ) x m – n .
در مثالی که حل میکنیم، m = 1 3 m = {\large\frac{1}{3}\normalsize} m = 3 1
y ( n ) = ( x 3 ) ( n ) = ( x 1 3 ) ( n ) = 1 3 ( 1 3 – 1 ) ( 1 3 – 2 ) ( 1 3 – 3 ) ⋯ ( 1 3 – n + 1 ) x 1 3 – n = 1 3 ⋅ ( – 2 3 ) ⋅ ( – 5 3 ) ⋅ ( – 8 3 ) ⋯ [ – ( n – 4 3 ) ] x 1 3 x n = 1 3 ⋅ ( – 1 ) n – 1 [ 2 3 ⋅ 5 3 ⋅ 8 3 ⋯ 3 n – 4 3 ] x 3 x n = ( – 1 ) n – 1 [ 2 ⋅ 5 ⋅ 8 ⋯ ( 3 n – 4 ) ] x 3 ( 3 x ) n \large {{y^{\left( n \right)}} = {\left( {\sqrt[\large 3\normalsize]{x}} \right)^{\left( n \right)}} }
= {{\left( {{x^{\large\frac{1}{3}\normalsize}}} \right)^{\left( n \right)}} } \\ \large
= {\frac{1}{3}\left( {\frac{1}{3} – 1} \right)}\kern0pt{\left( {\frac{1}{3} – 2} \right)\left( {\frac{1}{3} – 3} \right) \cdots}\kern0pt{ \left( {\frac{1}{3} – n + 1} \right){x^{\large\frac{1}{3}\normalsize – n}} } \\ \large
= {\frac{1}{3} \cdot \left( { – \frac{2}{3}} \right) \cdot}\kern0pt{ \left( { – \frac{5}{3}} \right) \cdot \left( { – \frac{8}{3}} \right) \cdots}\kern0pt{ \left[ { – \left( {n – \frac{4}{3}} \right)} \right]\frac{{{x^{\large\frac{1}{3}\normalsize}}}}{{{x^n}}} } \\ \large
= {\frac{1}{3} \cdot {\left( { – 1} \right)^{n – 1}}}\kern0pt{\left[ {\frac{2}{3} \cdot \frac{5}{3} \cdot \frac{8}{3} \cdots}\kern0pt{ \frac{{3n – 4}}{3}} \right]\frac{{\sqrt[\large 3\normalsize]{x}}}{{{x^n}}} } \\ \large
= {\frac{{{{\left( { – 1} \right)}^{n – 1}}\left[ {2 \cdot 5 \cdot 8 \cdots \left( {3n – 4} \right)} \right]\sqrt[\large 3\normalsize]{x}}}{{{{\left( {3x} \right)}^n}}}} y ( n ) = ( 3 x ) ( n ) = ( x 3 1 ) ( n ) = 3 1 ( 3 1 –1 ) ( 3 1 –2 ) ( 3 1 –3 ) ⋯ ( 3 1 – n + 1 ) x 3 1 – n = 3 1 ⋅ ( – 3 2 ) ⋅ ( – 3 5 ) ⋅ ( – 3 8 ) ⋯ [ – ( n – 3 4 ) ] x n x 3 1 = 3 1 ⋅ ( –1 ) n –1 [ 3 2 ⋅ 3 5 ⋅ 3 8 ⋯ 3 3 n –4 ] x n 3 x = ( 3 x ) n ( –1 ) n –1 [ 2 ⋅ 5 ⋅ 8 ⋯ ( 3 n –4 ) ] 3 x
که در آن، n ≥ 2 n \ge 2 n ≥ 2
y ′ ′ = ( – 1 ) 1 ⋅ 2 ⋅ x 3 ( 3 x ) 2 = – 2 x 3 9 x 2 = − 2 9 x 5 3 , \large {y^{\prime\prime} = \frac{{{{\left( { – 1} \right)}^1} \cdot 2 \cdot \sqrt[\large 3\normalsize]{x}}}{{{{\left( {3x} \right)}^2}}} }
= { – \frac{{2\sqrt[\large 3\normalsize]{x}}}{{9{x^2}}} }
= {- \frac{2}{{9\sqrt[3]{{{x^5}}}}},} y ′′ = ( 3 x ) 2 ( –1 ) 1 ⋅ 2 ⋅ 3 x = – 9 x 2 2 3 x = − 9 3 x 5 2 ,
y ′ ′ ′ = ( – 1 ) 2 ⋅ 2 ⋅ 5 ⋅ x 3 ( 3 x ) 3 = 10 x 3 27 x 3 = 10 27 x 8 3 . \large {y^{\prime\prime\prime} = \frac{{{{\left( { – 1} \right)}^2} \cdot 2 \cdot 5 \cdot \sqrt[\large 3\normalsize]{x}}}{{{{\left( {3x} \right)}^3}}} }
= {\frac{{10\sqrt[\large 3\normalsize]{x}}}{{27{x^3}}} }
= {\frac{{10}}{{27\sqrt[\large 3\normalsize]{{{x^8}}}}}.} y ′′′ = ( 3 x ) 3 ( –1 ) 2 ⋅ 2 ⋅ 5 ⋅ 3 x = 27 x 3 10 3 x = 27 3 x 8 10 .
مثال ۱۵
معادله پارامتری یک بیضی به صورت زیر داده شده است:
x = a cos t , y = b sin t , \large {x = a\cos t,\;\;\;}\kern-0.3pt{y = b\sin t,} x = a cos t , y = b sin t ,
که در آن، a a a b b b t t t y y y x x x
حل: با مشتقگیری از تابع، داریم:
y ′ = y ’ x = y ’ t x ’ t = ( b sin t ) ′ ( a cos t ) ′ = b cos t – a sin t = – b a cot t , \large {y^\prime = {y’_x} = \frac{{{y’_t}}}{{{x’_t}}} }
= {\frac{{{{\left( {b\sin t} \right)}^\prime }}}{{{{\left( {a\cos t} \right)}^\prime }}} }
= {\frac{{b\cos t}}{{ – a\sin t}} }
= { – \frac{b}{a}\cot t,} y ′ = y ’ x = x ’ t y ’ t = ( a cos t ) ′ ( b sin t ) ′ = – a sin t b cos t = – a b cot t ,
y ′ ′ = y x x ′ ′ = ( y ’ x ) ’ t x ’ t = ( – b a cot t ) ′ ( a cos t ) ′ = ( – b a ) ( – 1 sin 2 t ) ( – a sin t ) = – b a 2 1 sin 3 t = – b a 2 csc 3 t , \large {y^{\prime\prime} = {y^{\prime\prime}_{xx}} = \frac{{{{\left( {{y’_x}} \right)}’_t}}}{{{x’_t}}} }
= {\frac{{{{\left( { – \frac{b}{a}\cot t} \right)}^\prime }}}{{{{\left( {a\cos t} \right)}^\prime }}} } \\ \large
= {\frac{{\left( { – \frac{b}{a}} \right)\left( { – \frac{1}{{{{\sin }^2}t}}} \right)}}{{\left( { – a\sin t} \right)}} }
= { – \frac{b}{{{a^2}}}\frac{1}{{{{\sin }^3}t}} }
= { – \frac{b}{{{a^2}}}{\csc ^3}t,} y ′′ = y xx ′′ = x ’ t ( y ’ x ) ’ t = ( a cos t ) ′ ( – a b cot t ) ′ = ( – a sin t ) ( – a b ) ( – s i n 2 t 1 ) = – a 2 b sin 3 t 1 = – a 2 b csc 3 t ,
y ′ ′ ′ = y x x x ′ ′ ′ = ( y x x ′ ′ ) ’ t x ’ t = ( – b a 2 csc 3 t ) ′ ( a cos t ) ′ = ( – b a 2 ) ⋅ 3 csc 2 t ⋅ ( csc t ) ′ ( – a sin t ) = – 3 b a 3 ⋅ csc 2 t ⋅ ( – cot t ) ⋅ csc t ( – sin t ) = – 3 b a 3 ⋅ csc 3 t cot t sin t = – 3 b a 3 csc 4 t cot t . \large {y^{\prime\prime\prime} = {y^{\prime\prime\prime}_{xxx}} = \frac{{{{\left( {{y^{\prime\prime}_{xx}}} \right)}’_t} }}{{{x’_t}}} }
= {\frac{{{{\left( { – \frac{b}{{{a^2}}}{{\csc }^3}t} \right)}^\prime }}}{{{{\left( {a\cos t} \right)}^\prime }}} }
= {\frac{{\left( { – \frac{b}{{{a^2}}}} \right) \cdot 3{{\csc }^2}t \cdot {{\left( {\csc t} \right)}^\prime }}}{{\left( { – a\sin t} \right)}} } \\ \large
= { – \frac{{3b}}{{{a^3}}} \cdot \frac{{{{\csc }^2}t \cdot \left( { – \cot t} \right) \cdot \csc t}}{{\left( { – \sin t} \right)}} }
= { – \frac{{3b}}{{{a^3}}} \cdot \frac{{{{\csc }^3}t\cot t}}{{\sin t}} }
= { – \frac{{3b}}{{{a^3}}}{\csc ^4}t\cot t.} y ′′′ = y xxx ′′′ = x ’ t ( y xx ′′ ) ’ t = ( a cos t ) ′ ( – a 2 b csc 3 t ) ′ = ( – a sin t ) ( – a 2 b ) ⋅ 3 csc 2 t ⋅ ( csc t ) ′ = – a 3 3 b ⋅ ( – sin t ) csc 2 t ⋅ ( – cot t ) ⋅ csc t = – a 3 3 b ⋅ sin t csc 3 t cot t = – a 3 3 b csc 4 t cot t .
مثال ۱۶
مشتق سوم تابعی با معادله x 2 + 3 x y + y 2 = 1 {x^2} + 3xy + {y^2} = 1 x 2 + 3 x y + y 2 = 1
حل: مشتقگیری از معادله بالا نسبت به x x x
( x 2 + 3 x y + y 2 ) ′ = 1 ′ , ⇒ 2 x + 3 ( x ’ y + x y ’ ) + 2 y y ’ = 0 , ⇒ 2 x + 3 y + 3 x y ’ + 2 y y ’ = 0 , ⇒ 2 x + 3 y + ( 3 x + 2 y ) y ’ = 0 , ⇒ y ’ = – 2 x + 3 y 3 x + 2 y . \large {{\left( {{x^2} + 3xy + {y^2}} \right)^\prime } = {1^\prime },\;\;}\Rightarrow
{2x + 3\left( {x’y + xy’} \right) + 2yy’ = 0,\;\;}\\ \large \Rightarrow
{2x + 3y + 3xy’ + 2yy’ = 0,\;\;}\Rightarrow
{2x + 3y + \left( {3x + 2y} \right)y’ = 0,}\\ \large \Rightarrow
{y’ = – \frac{{2x + 3y}}{{3x + 2y}}.} ( x 2 + 3 x y + y 2 ) ′ = 1 ′ , ⇒ 2 x + 3 ( x ’ y + x y ’ ) + 2 yy ’ = 0 , ⇒ 2 x + 3 y + 3 x y ’ + 2 yy ’ = 0 , ⇒ 2 x + 3 y + ( 3 x + 2 y ) y ’ = 0 , ⇒ y ’ = – 3 x + 2 y 2 x + 3 y .
از عبارت اخیر نیز مشتق میگیریم:
y ′ ′ = ( – 2 x + 3 y 3 x + 2 y ) ′ = 5 y – 5 x y ’ ( 3 x + 2 y ) 2 . \large {y^{\prime\prime} = {\left( { – \frac{{2x + 3y}}{{3x + 2y}}} \right)^\prime } }
= {\frac{{5y – 5xy’}}{{{{\left( {3x + 2y} \right)}^2}}}.} y ′′ = ( – 3 x + 2 y 2 x + 3 y ) ′ = ( 3 x + 2 y ) 2 5 y –5 x y ’ .
با جایگذاری توصیف ضمنی مشتق اول، داریم:
y ′ ′ = 5 y – 5 x y ’ ( 3 x + 2 y ) 2 = 5 y – 5 x ( – 2 x + 3 y 3 x + 2 y ) ( 3 x + 2 y ) 2 = 5 y ( 3 x + 2 y ) + 5 x ( 2 x + 3 y ) ( 3 x + 2 y ) 3 = 15 x y + 10 y 2 + 10 x 2 + 15 x y ( 3 x + 2 y ) 3 = 10 ( x 2 + 3 x y + y 2 ) ( 3 x + 2 y ) 3 . \large {y^{\prime\prime} = \frac{{5y – 5xy’}}{{{{\left( {3x + 2y} \right)}^2}}} }
= {\frac{{5y – 5x\left( { – \frac{{2x + 3y}}{{3x + 2y}}} \right)}}{{{{\left( {3x + 2y} \right)}^2}}} }
= {\frac{{5y\left( {3x + 2y} \right) + 5x\left( {2x + 3y} \right)}}{{{{\left( {3x + 2y} \right)}^3}}} } \\ \large
= {\frac{{15xy + 10{y^2} + 10{x^2} + 15xy}}{{{{\left( {3x + 2y} \right)}^3}}} }
= {\frac{{10\left( {{x^2} + 3xy + {y^2}} \right)}}{{{{\left( {3x + 2y} \right)}^3}}}.} y ′′ = ( 3 x + 2 y ) 2 5 y –5 x y ’ = ( 3 x + 2 y ) 2 5 y –5 x ( – 3 x + 2 y 2 x + 3 y ) = ( 3 x + 2 y ) 3 5 y ( 3 x + 2 y ) + 5 x ( 2 x + 3 y ) = ( 3 x + 2 y ) 3 15 x y + 10 y 2 + 10 x 2 + 15 x y = ( 3 x + 2 y ) 3 10 ( x 2 + 3 x y + y 2 ) .
از آنجایی که x 2 + 3 x y + y 2 = 1 {x^2} + 3xy + {y^2} = 1 x 2 + 3 x y + y 2 = 1 y ′ ′ y^{\prime\prime} y ′′
y ′ ′ = 10 ( 3 x + 2 y ) 3 \large y^{\prime\prime} = \frac{{10}}{{{{\left( {3x + 2y} \right)}^3}}} y ′′ = ( 3 x + 2 y ) 3 10
اکنون برای بهدست آوردن مشتق سوم، یک بار دیگر مشتق میگیریم:
y ′ ′ ′ = [ 10 ( 3 x + 2 y ) 3 ] ′ = – 30 ( 3 + 2 y ’ ) ( 3 x + 2 y ) 4 = – 90 + 60 y ’ ( 3 x + 2 y ) 4 . \large {y^{\prime\prime\prime} = {\left[ {\frac{{10}}{{{{\left( {3x + 2y} \right)}^3}}}} \right]^\prime } }
= { – \frac{{30\left( {3 + 2y’} \right)}}{{{{\left( {3x + 2y} \right)}^4}}} }
= { – \frac{{90 + 60y’}}{{{{\left( {3x + 2y} \right)}^4}}}.} y ′′′ = [ ( 3 x + 2 y ) 3 10 ] ′ = – ( 3 x + 2 y ) 4 30 ( 3 + 2 y ’ ) = – ( 3 x + 2 y ) 4 90 + 60 y ’ .
با جایگذاری مشتق اول در عبارت بالا، توصیف نهایی مشتق مرتبه سوم بهصورت زیر بهدست میآید:
y ′ ′ ′ = – 90 + 60 y ’ ( 3 x + 2 y ) 4 = – 90 + 60 ⋅ ( – 2 x + 3 y 3 x + 2 y ) ( 3 x + 2 y ) 4 = – 90 ( 3 x + 2 y ) – 60 ( 2 x + 3 y ) ( 3 x + 2 y ) 5 = – 150 ( 3 x + 2 y ) 5 . \large {y^{\prime\prime\prime} = – \frac{{90 + 60y’}}{{{{\left( {3x + 2y} \right)}^4}}} }
= { – \frac{{90 + 60 \cdot \left( { – \frac{{2x + 3y}}{{3x + 2y}}} \right)}}{{{{\left( {3x + 2y} \right)}^4}}} } \\ \large
= { – \frac{{90\left( {3x + 2y} \right) – 60\left( {2x + 3y} \right)}}{{{{\left( {3x + 2y} \right)}^5}}} }
= { – \frac{{150}}{{{{\left( {3x + 2y} \right)}^5}}}.} y ′′′ = – ( 3 x + 2 y ) 4 90 + 60 y ’ = – ( 3 x + 2 y ) 4 90 + 60 ⋅ ( – 3 x + 2 y 2 x + 3 y ) = – ( 3 x + 2 y ) 5 90 ( 3 x + 2 y ) –60 ( 2 x + 3 y ) = – ( 3 x + 2 y ) 5 150 .
مثال ۱۷
مشتق مرتبه دوم تابعی با معادله x + y = e x – y x + y = {e^{x – y}} x + y = e x – y
حل: با مشتقگیری از دو سمت معادله بالا نسبت به x x x
( x + y ) ′ = ( e x – y ) ′ , ⇒ 1 + y ’ = e x – y ⋅ ( x – y ) ′ , ⇒ 1 + y ’ = e x – y ( 1 – y ’ ) = e x – y – e x – y y ’ , ⇒ y ’ + e x – y y ’ = e x – y – 1 , ⇒ y ’ = e x – y – 1 e x – y + 1 . \large {{\left( {x + y} \right)^\prime } = {\left( {{e^{x – y}}} \right)^\prime },\;\;}\Rightarrow
{1 + y’ = {e^{x – y}} \cdot {\left( {x – y} \right)^\prime },\;\;}\\ \large \Rightarrow
{1 + y’ = {e^{x – y}}\left( {1 – y’} \right) = {e^{x – y}} – {e^{x – y}}y’,\;\;}\\ \large \Rightarrow
{y’ + {e^{x – y}}y’ = {e^{x – y}} – 1,\;\;}\Rightarrow
{y’ = \frac{{{e^{x – y}} – 1}}{{{e^{x – y}} + 1}}.} ( x + y ) ′ = ( e x – y ) ′ , ⇒ 1 + y ’ = e x – y ⋅ ( x – y ) ′ , ⇒ 1 + y ’ = e x – y ( 1– y ’ ) = e x – y – e x – y y ’ , ⇒ y ’ + e x – y y ’ = e x – y –1 , ⇒ y ’ = e x – y + 1 e x – y –1 .
با ادامه مشتقگیری، مشتق مرتبه دوم نیز بهدست میآید:
y ′ ′ = ( e x – y – 1 e x – y + 1 ) ′ = 2 e x – y ( 1 – y ’ ) ( e x – y + 1 ) 2 . \large {y^{\prime\prime} = {\left( {\frac{{{e^{x – y}} – 1}}{{{e^{x – y}} + 1}}} \right)^\prime } }
= {\frac{{2{e^{x – y}}\left( {1 – y’} \right)}}{{{{\left( {{e^{x – y}} + 1} \right)}^2}}}.} y ′′ = ( e x – y + 1 e x – y –1 ) ′ = ( e x – y + 1 ) 2 2 e x – y ( 1– y ’ ) .
با جایگذاری عبارت مشتق اول در عبارت اخیر، مشتق دوم بهصورت زیر درخواهد آمد:
y ′ ′ = 2 e x – y ( 1 – y ’ ) ( e x – y + 1 ) 2 = 2 e x – y ( 1 – e x – y – 1 e x – y + 1 ) ( e x – y + 1 ) 2 = 2 e x – y ⋅ e x – y + 1 – e x – y + 1 e x – y + 1 ( e x – y + 1 ) 2 = 4 e x – y ( e x – y + 1 ) 3 . \large {y^{\prime\prime} = \frac{{2{e^{x – y}}\left( {1 – y’} \right)}}{{{{\left( {{e^{x – y}} + 1} \right)}^2}}} }
= {\frac{{2{e^{x – y}}\left( {1 – \frac{{{e^{x – y}} – 1}}{{{e^{x – y}} + 1}}} \right)}}{{{{\left( {{e^{x – y}} + 1} \right)}^2}}} } \\ \large
= {\frac{{2{e^{x – y}} \cdot \frac{{\cancel{e^{x – y}} + 1 – \cancel{e^{x – y}} + 1}}{{{e^{x – y}} + 1}}}}{{{{\left( {{e^{x – y}} + 1} \right)}^2}}} }
= {\frac{{4{e^{x – y}}}}{{{{\left( {{e^{x – y}} + 1} \right)}^3}}}.} y ′′ = ( e x – y + 1 ) 2 2 e x – y ( 1– y ’ ) = ( e x – y + 1 ) 2 2 e x – y ( 1– e x – y + 1 e x – y –1 ) = ( e x – y + 1 ) 2 2 e x – y ⋅ e x – y + 1 e x – y + 1– e x – y + 1 = ( e x – y + 1 ) 3 4 e x – y .
اکنون از معادله اصلی استفاده میکنیم که طبق آن:
e x – y = x + y \large {e^{x – y}} = x + y e x – y = x + y
در نهایت، عبارت زیر برای مشتق مرتبه دوم بهدست میآید:
y ′ ′ = 4 e x – y ( e x – y + 1 ) 3 = 4 ( x + y ) ( x + y + 1 ) 3 . \large {y^{\prime\prime} = \frac{{4{e^{x – y}}}}{{{{\left( {{e^{x – y}} + 1} \right)}^3}}} }
= {\frac{{4\left( {x + y} \right)}}{{{{\left( {x + y + 1} \right)}^3}}}.} y ′′ = ( e x – y + 1 ) 3 4 e x – y = ( x + y + 1 ) 3 4 ( x + y ) .
اگر به موضوعات مرتبط با این مطلب علاقهمندید، پیشنهاد میکنیم آموزشهای زیر را نیز ببینید:
^^
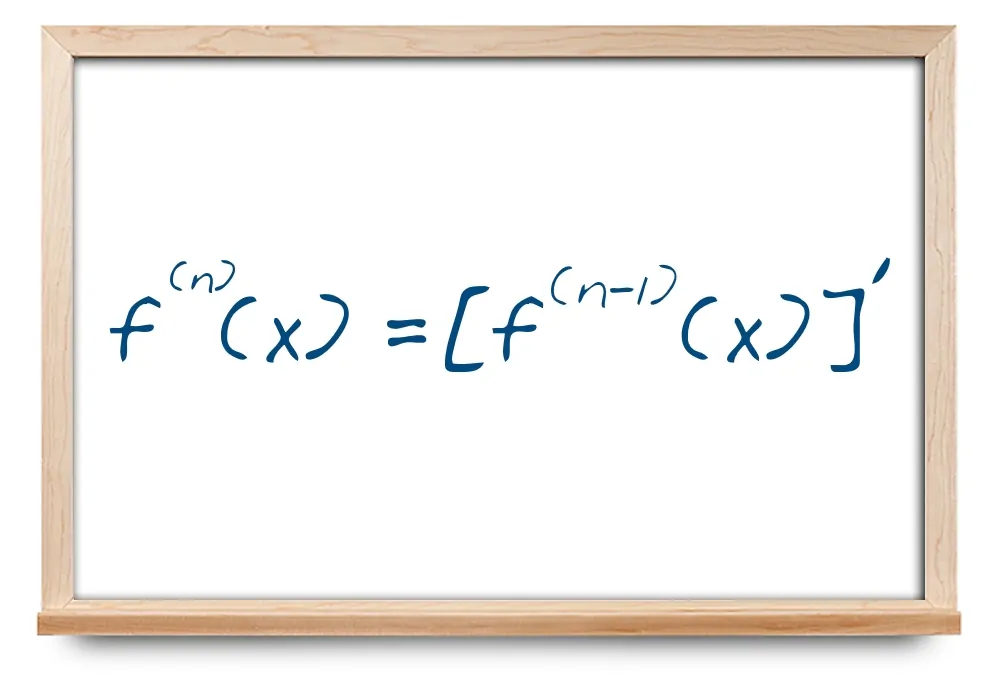
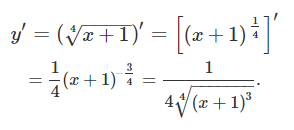
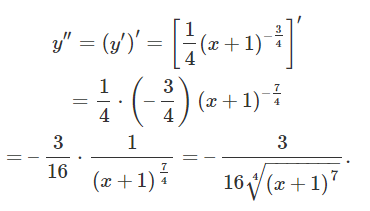
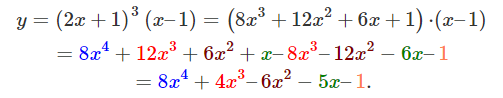













مثال 9 چرا sgn رفت بالا :؟؟؟/////
سلام و وقت بخیر؛
تابع sign(x)، تابع علامت است. به دلیل ضرب این تابع در کل عبارت مخرج، انتقال آن به صورت کسر، مانعی ندارد.
از همراهی شما با مجله فرادرس سپاسگزاریم
y=1/3x^3 مشتق چند است؟
سلام. مشتق تابع y=3x31 بهصورت زیر محاسبه میشود:
(3x31)’=(31x−3)’=−3(31)x−4=−x−4=x4−1
موفق باشید.
هر ۱۷ تا مثالش اسون بود
لطفا از توابع کسری با صورت و مخرج متغییر دار هم مثالی حل کنید :/
سلام. برای مشاهده مثالهای مشتق توابع کسری، پیشنهاد میکنیم به آموزش «مشتق توابع کسری — به زبان ساده» مراجعه کنید.
از همراهیتان، خوشحالیم.
خیلی عالی بود
ولی ای کاش مشتق مرتبه n ام سینوس و کسینوس وقتی x ضریب داره رو هم میذاشتید به اثباتش نیاز داشتم.