اعداد اعشاری — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

اَعشار جمع واژه عربی عُشر (به معنی یکدهم چیزی) است. به این ترتیب، اعشار معادل با یکدهمها است. چیزی که ما در این آموزش از مجله فرادرس با آن سر و کار داریم، همین یکدهمها هستند که اعداد اعشاری را میسازند. در ادامه، با اعداد اعشاری و عملیات روی آنها آشنا میشویم.
فیلم آموزشی اعداد اعشاری
آشنایی با اعداد اعشاری
اعداد اعشاری (Decimal Numbers) اعدادی هستند که برای نمایش مقادیری به کار میروند که با اعداد شمارشی عادی نمیتوان آنها را بیان کرد. اعشار را با ممیز (یعنی تمایز دهنده) نمایش میدهیم. در دستور خط فارسی، علامت ممیز یک خط کوچک کج است. برای مثال، یک و نیم را به صورت ۱٫۵ مینویسیم. در زبان انگلیسی، ممیز را با نقطه نشان میدهند. مثلاً همان عدد یک و نیم در زبان انگلیسی به صورت $$ 1.5$$ نوشته میشود.
تذکر ۱: توجه کنید که علامت کسر (/) با ممیز (٫) فرق دارد و اغلب به اشتباه به جای ممیز به کار میرود.
در ادامه، مفهوم اعشار را بیان میکنیم. شکل زیر را در نظر بگیرید. در این شکل، مربع بنفش سمت چپ یک واحد را نشان میدهد. به عبارت سادهتر میتوانیم بگوییم که ۱ مربع داریم. اگر این مربع را به ۱۰ قسمت مساوی تقسیم کنیم (مربع دوم در شکل)، هر یک از این بخشهای کوچکتر یکدهم مربع هستند. به بیان سادهتر، یک دهم معادل با «یکی از ده بخش» مربع است.
حال مربع سوم را در نظر بگیرید که به ۱۰۰ قسمت مساوی تقسیم شده است. هریک از این بخشهای کوچک در این مربع یکصدم آن (یکی از صد بخش) هستند.

اکنون به شکل زیر دقت کنید.
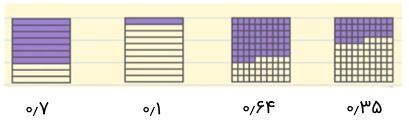
در شکل بالا، مربع سمت چپ به ۱۰ قسمت تقسیم شده است. بنابراین، در این مربع با یکدهمها سر و کار داریم. از این ۱۰ مربع، ۷ تای آنها رنگ شده است. بنابراین در مورد این مربع میتوانیم بگوییم که هیچ مربع کاملی نداریم و ۷ تا یکدهم از آن داریم. همانطور که میدانیم، در شمارش، اگر چیزی وجود نداشته باشد، عدد ۰ را به آن نسبت میدهیم. در نتیجه، اندازه بخش بنفش مربع سمت چپ شکل بالا، ۰ تا مربع کامل و ۷ تا یکدهم از مربع کامل است. این مقدار را به شکل ریاضی به صورت ۰٫۷ مینویسیم و آن را «هفتدهم» میخوانیم (عدد صفر را نمیخوانیم). «هفتدهم» همان «هفت تا یکدهم» است.
به طور مشابه برای مربع دوم از سمت چپ، عدد ۰٫۱ (یکدهم) را داریم.
اکنون مربع سوم از سمت چپ را در نظر بگیرید. این مربع به ۱۰۰ بخش تقسیم شده است. بنابراین، برای عدد مرتبط با این شکل میتوانیم بگوییم که ۰ تا مربع کامل و ۶ تا یکدهم و ۴ تا یکصدم از مربع داریم. در نتیجه، عدد مربوط به این مربع ۰٫۶۴ خواهد بود. دقت کنید که از بزرگترین واحد به کوچکترین واحد اعداد را مینویسیم (دهم، صدم، هزارم و...)؛ یعنی اگر نتوانستیم با واحدهای بزرگتر یک مقدار را توصیف کنیم، از واحدهای کوچکتر کمک میگیریم.
عدد ۰٫۶۴ را به صورت «شصتوچهار صدم» میخوانیم. از این نحوه خوانش نیز مشخص است که هر یکدهم برابر با ۱۰ تا یکصدم است. همچنین، هر یکصدم برابر با ۱۰ یکهزارم است و... .
مربع سمت راست شکل بالا نیز عدد ۰٫۳۵ را نشان میدهد.
مثال
اکنون شکل زیر را مشاهده کنید. میخواهیم عدد مربوط به بخشهای بنفش این شکل را بیان کنیم.
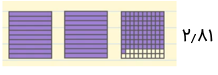
از بزرگترین واحد که مربع کامل است شروع میکنیم. در این شکل، تعداد ۲ مربع کامل داریم. علاوه بر این، ۸ تا یکدهم و ۱ تا یکصدم نیز داریم. بنابراین، عدد مورد نظر ۲٫۸۱ (دو و هشتادویک صدم) خواهد بود.
مثال
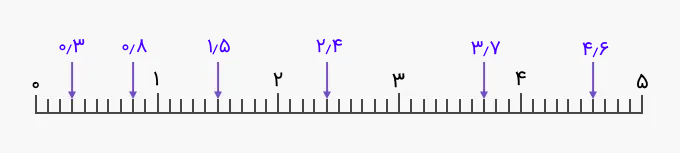
به عنوان یک مثال دیگر از اعداد اعشاری، شکل زیر را در نظر بگیرید که یک خطکش است. به اعداد اعشاری مشخص شده روی آن دقت کنید و سعی کنید با توجه به مطالبی که گفتیم درستی آنها را بررسی کنید.
ارزش ارقام در اعداد اعشاری
بد نیست از زاویه دیگری نیز به موضوع نگاه کنیم. عدد ۶۴٫۰ را در نظر بگیرید که میدانیم همان ۶۴ است. این عدد به معنی ۶ دهتایی و ۴ یکی است و چون بخشهای کوچکتری از یک واحد ندارد، بعد از ممیز عددی قرار نمیگیرد.
با یک مقایسه کوچک، مشاهده میکنیم که سمت راست ممیز، دهمها، صدمها، هزارمها و... و سمت چپ آن، دهگانها، صدگانها، هزارگانها و... را نمایش میدهند.
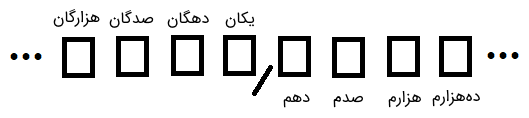
در سمت راستِ ممیزِ شکل بالا، هرچه به سمت راست میرویم، ارزش اعداد کم میشود. همچنین در سمت چپ ممیز، هرچه به سمت چپ میرویم، ارزش اعداد افزایش مییابد.
تذکر ۲: دقت کنید که وقتی ممیز در عددی به کار میرود، باید آن را با عدد بدون ممیز تمایز دهیم. برای مثال، عدد ۱٫۰۰۰ همان یک است و ۱۰۰۰ نمایانگر عدد هزار است.
تذکر ۳: همچنین به یاد داشته باشید که برای اعشار تنها از علامت ممیز (٫) یا نقطه (.) استفاده میشود. گاهی علامتهایی مانند ویرگول انگلیسی (,) برای جدا کردن هزارگانها در اعداد بزرگ (مثلاً قیمتها) به کار میرود که نباید آن را با ممیز اشتباه گرفت. برای مثال ۱,۰۰۰,۰۰۰ یک میلیون را نشان میدهد که از علامت ویرگول انگلیسی برای جداسازی ارقام هزارتایی در آن استفاده شده است.
تبدیل اعداد اعشاری به اعداد کسری
برای تبدیل اعداد اعشاری به اعداد کسری کافی است همان چیزی را که میخوانیم، بنویسیم. عدد ۰٫۲۵ را در نظر بگیرید.
این عدد را به صورت «بیستوپنج صدم» یا بیستوپنج تا از صد تا میخوانیم و آن را به شکل کسری $$ \frac {25} { 100} $$ مینویسیم. به همین ترتیب، چند مثال زیر را نیز داریم:
- ۰٫۱ برابر است با $$ \frac {1} { 10} $$
- ۰٫۰۱ برابر است با $$ \frac {1} { 100} $$
- 0٫۰۰۱ برابر است با $$ \frac { 1 } { 1000} $$
- ۰٫۵۴ برابر است با $$ \frac {54}{100}$$
- ۰٫۰۳۲ برابر است با $$ \frac{32}{1000}$$
حال عدد اعشاری ۲٫۳۵ را در نظر بگیرید. این عدد را به صورت «دو و سیوپنج صدم» میخوانیم و آن را به شکل کسری زیر نمایش میدهیم:
$$ 2\frac {35}{100}$$
در واقع، $$ 2$$ واحد کامل و کسر $$ \frac{35}{100}$$ را داریم.
حال میخواهیم کسر $$ \frac {51}{100}$$ را به صورت یک عدد اعشاری بنویسیم. این کسر «پنجاهویک تا از صد تا» را نشان میدهد. واحد کامل نیز نداریم، به همین دلیل آن را به صورت 0٫۵۱ مینویسیم.
جمع اعداد اعشاری
برای جمع اعداد اعشاری، مراحل زیر را طی میکنیم:
- یکی از اعداد را در زیر دیگری به گونهای مینویسیم که ممیز آنها در زیر هم قرار گیرد.
- اگر تعداد ارقام سمت راست ممیز یک عدد با تعداد ارقام سمت راست ممیز عدد دیگر برابر نباشد، به اندازه مقدار اختلاف آنها جلوی عددی که ارقام کمتری دارد، صفر قرار میدهیم.
- ارقام متناظر را به صورت عمودی و از راست به چپ، به صورت عادی با هم جمع میکنیم.
مثال
میخواهیم دو عدد ۱٫۴۵۲ و ۱٫۳ را با هم جمع کنیم.
گامهای بیان شده به صورت زیر مشخص شدهاند:
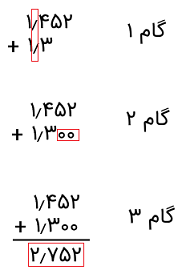
مثال
اکنون فرض کنید میخواهیم سه عدد ۳٫۲۵، ۰٫۰۷۵ و ۵ را با هم جمع کنیم.
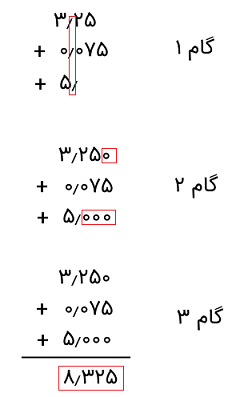
دلیل اضافه کردن صفر این است که در ارزش مقدار عدد تأثیری ندارد.
برای آشنایی بیشتر با جمع اعداد اعشاری، به آموزش «جمع اعداد اعشاری — به زبان ساده + تمرین و مثال» از مجله فرادرس مراجعه کنید.
تفریق اعداد اعشاری
برای تفریق اعداد اعشاری، گامهای زیر را طی میکنیم:
- یکی از اعداد را در زیر دیگری به گونهای مینویسیم که ممیز آنها در زیر هم قرار گیرد.
- اگر تعداد ارقام سمت راست ممیز یک عدد با تعداد راقام سمت راست ممیز عدد دیگر برابر نباشد، به اندازه مقدار اختلاف آنها جلوی عددی که ارقام کمتری دارد، صفر قرار میدهیم.
- ارقام متناظر را به صورت عمودی و از راست به چپ از هم کم میکنیم.
مثال
فرض کنید میخواهیم عدد ۰٫۰۳ را از ۱٫۱ کم کنیم. گامهای زیر را طی میکنیم:
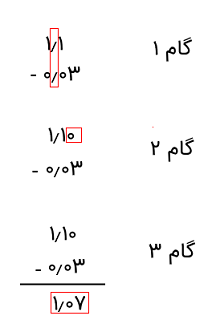
مثال
در یک مثال دیگر، عدد ۰٫۵۵ را از ۷٫۰۰۵ کم میکنیم:
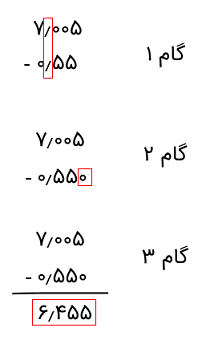
برای آشنایی بیشتر با تفریق اعداد اعشاری، به آموزش «تفریق اعداد اعشاری — به زبان ساده + مثال و تمرین» از مجله فرادرس مراجعه کنید.
ضرب اعداد اعشاری
برای ضرب اعداد اعشاری، گامهای زیر را انجام میدهیم:
- فرض میکنیم ممیزها وجود ندارند و اعداد را به صورت عادی در هم ضرب میکنیم.
- تعداد ارقام سمت راست ممیز دو عدد را با هم جمع کرده و به اندازه آنها از سمت راست اعشار جدا میکنیم.
مثال
برای مثال، فرض کنید میخواهیم دو عدد ۰٫۰۳ و ۱٫۱ را در هم ضرب کنیم. اگر ممیز این دو عدد را در نظر نگیریم، دو عدد ۳ و ۱۱ را خواهیم داشت.
برای این دو عدد، داریم:
۳۳ = ۱۱ × ۳
اکنون باید ممیز را قرار دهیم. عدد ۰٫۰۳ دو رقم اعشار و عدد ۱٫۱ یک رقم اعشار دارد که مجموع آنها سه رقم اعشار است.
حال از سمت راست، سه رقم اعشار را از عدد ۳۳ جدا میکنیم که نتیجه آن ۰٫۰۳۳ است. در نتیجه، میتوان نوشت:
۰٫۰۳۳ = ۱٫۱ × ۰٫۰۳
شاید این پرسش برایتان به وجود بیاید که چرا این کار را انجام دادیم. وقتی دو عدد بدون اعشار را در هم ضرب میکنیم، در حقیقت ممیز آن را به سمت راست حرکت میدهیم:
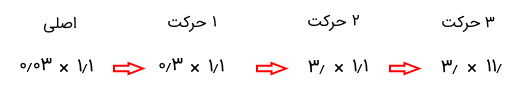
بنابراین، باید تأثیر جابهجایی ارقام اعشاری را در نهایت اعمال کنیم:

مثال
میخواهیم دو عدد اعشاری ۰٫۲۵ و ۰٫۲ را در یکدیگر ضرب کنیم.
ابتدا آنها را بدون اعشار در نظر میگیریم و آنها را در هم ضرب میکنیم. بنابراین، داریم:
۵۰ = ۲ × ۲۵
برای عدد ۰٫۲۵ دو رقم اعشار و برای عدد ۰٫۲ یک رقم اعشار را در نظر نگرفتیم که مجموع آنها سه رقم اعشار است. بنابراین، سه رقم اعشار را از ۵۰ جدا میکنیم، که نتیجه آن برابر با ۰٫۰۵۰ است.
مثال
میخواهیم حاصلضرب دو عدد ۱۰۲ و ۰٫۲۲ را محاسبه کنیم. مطابق آنچه گفتیم، اعشارها را در نظر نمیگیریم. بنابراین، حاصلضرب دو عدد بدون در نظر گرفتن اعشار به صورت زیر است:
۲۲۴۴ = ۲۲ × ۱۰۲
اکنون برای به دست آوردن نتیجه مورد نظر، دو رقم اعشار را جدا میکنیم و خواهیم داشت:
۲۲٫۴۴ = ۰٫۲۲ × ۱۰۲
تقسیم اعداد اعشاری
برای محاسبه تقسیمی که یکی یا هر دو عدد آن اعشاری هستند، ابتدا اعشار هر دو عدد را با ضرب در یک عدد مناسب حذف میکنیم و سپس تقسیم اعشاری را انجام میدهیم.
مثال
برای مثال، فرض کنید میخواهیم ۱۵ را بر ۰٫۲ تقسیم کنیم. برای انجام تقسیم، باید اعشار ۰٫۲ را حذف کنیم. برای این کار کافی است آن را در ۱۰ ضرب کرده و به عدد ۲ برسیم. عدد ۱۵ را نیز باید در ۱۰ ضرب کنیم تا این دو ضرب در نتیجه نهایی تقسیم بی اثر باشند. به عبارت دیگر، میتوان نوشت:
$$ \frac {15} {0.2} = \frac {15 \times 10 } { 0.2 \times 10 } = \frac {150}{2}$$
حاصل تقسیم ۱۵۰ بر ۲ برابر با ۷۵ است و در نتیجه، حاصل تقسیم ۱۵ بر ۰٫۲ نیز ۷۵ خواهد بود.
مثال
میخواهیم عدد ۶٫۴ را بر ۰٫۴ تقسیم کنیم. مشابه مثال قبل، داریم:
$$ \frac {6.4}{0.4} = \frac {6.4 \times 10}{0.4\times 10} = \frac {64}{4} = 16 $$
مثال
میخواهیم عدد ۰٫۳۵۹ را بر ۰٫۱۱ تقسیم کنیم (تا یک رقم اعشار).
ابتدا با ضرب عدد مناسب، اعشار دو عدد را از بین میبریم:
$$ \frac {0.359}{0.11} = \frac { 0.359 \times 1000} { 0.11 \times 1000} = \frac { 359}{110}$$
حاصل این تقسیم، مانند تقسیم دو عدد طبیعی عادی به دست میآید:
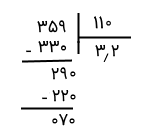
آزمون اعداد اعشاری
در این بخش به منظور آشنایی بیشتر و درک بهتر اعداد اعشاری، تعدادی پرسش چهار گزینهای طرح شده است.
اگر حاصلضرب دو عدد برابر ۴۲/۶۳ و یکی از دو عدد برابر ۲/۱ باشد، عدد دیگر برابر است با:
۲۰/۳
۲/۰۳
۰/۲۰۳
۲۰۳
حاصلضرب دو عدد برابر ۴۲/۶۳ و یکی از دو عدد برابر ۲/۱ است. عدد دوم را میخواهیم بهدست آوریم. فرض کنید عدد دوم برابر A است:
$$A \times 2.1 = 42. 63 $$
برای بهدست آوردن A باید ۴۲/۶۳ را بر ۲/۱ تقسیم کنیم. برای انجام این کار اعشار ۲/۱ را به سمت راست حرکت میدهیم. با قرار دادن اعشار پس از عدد ۱ در ۲/۱ به عددی صحیح میرسیم. از آنجا که علامت اعشار در ۲/۱، یک رقم به سمت راست حرکت میکند، علامت اعشار در ۴۲/۶۳ را نیز یک رقم به سمت راست حرکت میدهیم:
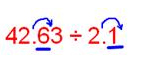
بنابراین، با تقسیم ۴۲۶/۳ بر ۲۱ میتوانیم A را بهدست آوریم. خارج قسمت این تقسیم و در نتیجه مقدار A برابر ۲۰/۳ بهدست میآید.
قیمت ۹/۲۵ متر از پارچهای برابر ۴۲۵/۵۰ تومان است. قسمت هر متر پارچه چه مقدار است؟
۴۶۰
۴۶
۴۶۰۰
۴/۶
برای بهدست آوردن قیمت هر متر پارچه باید قیمت کل آن را بر ۹/۲۵ متر پارچه تقسیم کنیم. برای تقسیم ۴۲۵/۵۰ بر ۹/۲۵، باید اعشار عدد ۹/۲۵ را تا جایی به سمت راست حرکت دهیم که به عدد صحیح برسیم. برای رسیدن به عدد صحیح، تنها کافی است اعشار عدد ۹/۲۵ را دو رقم به سمت راست حرکت دهیم. به طور مشابه، علامت اعشار در عدد ۴۲۵/۵۰ را نیز، دو رقم به سمت راست حرکت میدهیم و به عدد ۴۲۵۵۰ میرسیم. در ادامه، برای بهدست آوردن قیمت هر متر پارچه کافی است عدد ۴۲۵۵۰ را بر ۹۲۵ تقسیم کنیم. قیمت هر متر پارچه، مقدار ۴۶ تومان بهدست میآید.
جرم پارچ خالی آبی برابر ۰/۶۴ کیلوگرم و جرم این پارچ پر از آب برابر ۱/۷۲۸ کیلوگرم است. جرم آب داخل پارج چه مقدار است؟
۱/۸۸ کیلوگرم
۱/۰۸۸ کیلوگرم
۱/۸۰۸ کیلوگرم
۰/۸ کیلوگرم
بر طبق صورت مسئله، جرم پارچ خالی برابر ۰/۶۴ و جرم پارچ پر از آب برابر ۱/۷۲۸ کیلوگرم است. برای بهدست آوردن جرم آبِ داخل پارچ باید جرم پارچِ پر را از جرم پارچ خالی کم کنیم.

بنابراین، جرم آبِ داخل پارچ برابر ۱/۰۸۸ کیلوگرم است.
دوچرخهسواری در مرحله اول مسابقه مسافت ۱۳۶/۶۵ کیلومتر، در مرحله دوم ۱۳۶/۶۵ کیلومتر و در مرحله سوم ۱۶۲/۶۲ کیلومتر را طی کرده است. اگر مسیر کل مسابقه برابر ۱۰۰۰ کیلومتر باشد، مسافت باقیمانده چه مقدار است؟
۴۴۳/۹۳ کیلومتر
۳۴۳/۹۳ کیلومتر
۴۴۵/۰۷ کیلومتر
۵۵۴/۹۳ کیلومتر
این مسئله در دو بخش حل میشود. ابتدا باید مسافت کل طی شده توسط دوچرخهسوار را در سه مرحله بهدست آوریم. برای انجام این کار باید مسافتهای طی شده در سه مرحله را به صورت زیر با یکدیگر جمع کنیم:

بنابراین، در سه مرحله مسابقه، دوچرخهسوار مسافت ۴۴۵/۰۷ کیلومتر را طی کرده است. برای آنکه مسافت باقیمانده را بهدست آوریم، باید عدد بهدست آمده، یعنی ۴۴۵/۰۷ کیلومتر، را از ۱۰۰۰ کیلومتر کم کنیم.

در نتیجه، دوچرخهسوار پس از پیمودن مسافت ۵۵۴/۹۳ کیلومتر به خط پایان میرسد.
از چاه پر از آبی در مرحله اول ۱۸۴/۵ لیتر، در مرحله دوم ۱۲۸/۷۵ لیتر و در مرحله سوم، ۸۴/۵ لیتر آب خارج میکنیم. اگر پس از خروج این مقدار آب از چاه، مقدار آب موجود در چاه برابر ۱۶۰ لیتر باشد، مقدار کل آب موجود در چاه چه مقدار بود؟
۵۵۷/۷۵ لیتر
۵۵۰/۰۰ لیتر
۴۵۷/۵۷ لیتر
هیچکدام
برای آنکه بدانیم چاه قبل از خارج کردن آب از آن، چاه چه مقدار آب داشت باید مقدار برداشت آب از چاه در سه مرحله را با مقدار آب باقیمانده در آن با یکدیگر جمع کنیم:

۲۴۰ جعبه داریم که داخل هر کدام ۲۵ بسته قهوه وجو دارد. اگر جرم هر بسته قهوه برابر ۰/۶۲ کیلوگرم باشد، جرم تمام قهوهها چه مقدار است؟
۳۷۱۲۰/۰۰ کیلوگرم
۳۷۱۲/۰۰۰ کیلوگرم
۳۷۱۲۰۰/۰ کیلوگرم
۳۷۱/۲۰۰۰ کیلوگرم
برای بهدست آوردن جرمِ کل قهوه باید جرم هر جعبه را محاسبه کنیم، سپس جرم بهدست آمده را در ۲۴۰ ضرب کنیم. چگونه جرم هر جعبه را بهدست میآوریم؟ داخل هر جعبه، ۲۵ بسته قهوه وجود دارد که جرم هر کدام برابر ۰/۶۲ کیلوگرم است. بنابراین، برای یافتن جرم هر جعبه، تنها کافی است عدد ۰/۶۲ کیلوگرم را در ۲۵ ضرب کنیم. به یاد داشته باشید که به هنگام ضرب دو عدد اعشاری یا یک عدد اعشاری با یک عدد صحیح،از علامت اعشار چشمپوشی میکنیم و دو عدد را همانند دو عدد صحیح در یکدیگر ضرب، سپس علامت اعشار را به پاسخ بهدست آمده اعمال میکنیم.
از اینرو، به هنگام ضرب دو عدد ۲۵ و ۰/۶۲ از علامت اعشاری ۰/۶۲ چشمپوشی میکنیم و آنها را به صورت زیر در یکدیگر ضرب میکنیم:

عدد ۲۵ اعشار ندارد و عدد ۰/۶۲، دو رقم اعشار دارد. بنابراین، عدد ۱۵۵۰ پس از قرار دادن اعشار برای آن به صورت ۱۵/۵۰ نوشته میشود. از اینرو، جرم قهوه موجود در هر جعبه برابر ۱۵/۵۰ کیلوگرم است. در قدم بعدی، جرم ۲۴۰ جعبه را بهدست میآوریم. برای انجام این کار، ابتدا ۱۵/۵۰ را در ۲۴۰ ضرب میکنیم. به طور مشابه برای محاسبه حاصلضرب این دو عدد، از اعشار ۱۵/۵۰ چشمپوشی و پس از محاسبه ضرب، اعشار را اعمال میکنیم.

عدد ۲۴۰ اعشار ندارد و عدد ۱۵/۵۰، دو رقم اعشار دارد. بنابراین، عدد ۳۷۱۲۰۰۰ پس از قرار دادن اعشار برای آن به صورت ۳۷۱۲۰/۰۰ نوشته میشود. در نتیجه، جرم کل قهوه موجود برابر ۳۷۱۲۰/۰۰ کیلوگرم است.
حاصل تقسیم ۱/۲۵ بر ۰/۰۵ کدام است؟
۰/۵
۵
۰/۰۵
۵۰
برای بهدست آوردن حاصل تقسیم ۱/۲۵ بر ۰/۰۵، ابتدا آنها را به صورت کسری مینویسیم:
$$\frac { 1/25 } { 0/05 } $$
عدد ۱/۲۵ را میتوانیم به صورت $$\frac { 125 } { 100} $$ و عدد ۰/۰۵ را نیز میتوانیم به صورت $$\frac { 5 } { 100} $$ بنویسیم.
$$\frac { \frac { 125 } { 100 } } {\frac { 5 } { 100 }} $$
تقسیم دو کسر فوق را میتوانیم به صورت زیر به ضرب دو کسر تبدیل کنیم.
$$\frac { 125 } { 100} \times { 100 } = 5 $$











راه تشخیص کسر از ممیز چیه؟
سلام من میخوام وقتی یک عدد اعشار رو ضرب کردم در عدد صحیح بعدش. تبدیل کنم به عدد صحیح
جواب من ۰/۰۲ ؟= ۲ * ۰/۰۱
جواب استاد ۲۰ درومده
چجوری ۲۰ رو که صحیحه بدست بیارم؟
سلام ببخشید چه طور
تقسیم لشاری بزرگ را ساده کنیم
باتشکر
بهترین سایت ❤???
سلام ممنون عاااالی بود
سلام مهبد عزیز.
به آموزش «تقسیم اعداد اعشاری — آموزش با مثال و به زبان ساده» مراجعه کنید.
شاد و پیروز باشید.
سلام
من امروز امتحان ریاضی داشتم و معلم یه سئوال داده بود که :
کسر ۲ بر روی ۱۱ رو به صورت اعشار بنویسید و نوع آن را مشخص کنید
من در این سوال باید چکار میکردم؟
چگونه جواب به دست میاد؟
عالی توضیح دادید
سلام مهدی عزیز.
احتمالاً با مطالعه آموزش «کسر متعارفی — به زبان ساده» به پاسخ پرسشتان خواهید رسید.
سالم و موفق باشید.
برای من خیلی مفیدبود
چقدر خوب میشد اگه کسر های اعشاری ای که صورت ان از مخرج کوچکتر است و به اعداد 10 یا 100 یا 1000 یا … بخش پذیر نمیشه رو بگید
سلام.
پیشنهاد میکنیم مطلب «اعداد گویا — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» را مطالعه کنید.
موفق باشید.
سلام.
خوشحالیم که این آموزش برایتان مفید بوده است.
سپاس از همراهیتان.
لذت بردم از دیدن مناظر زیبایی که در این مقاله بکار برده بودید
وقتی به عددی اعشار میدهیم چه تغیری در توان اون ایجاد میشه ؟ یعنی اگر من اعشار عدد مثلا 10 به توان 3 را بخواهم بردارم باید از توان کم شود یا اضافه اگر کم شود اعشار به راست میرود یا چپ ؟
واقعه عالی خیلی مفهومی بود متشکرم
عاااااااااااااااااااااااااااااااااااااا لیییییییییییییییییییییییییییییییییییی
ممنون از زحماتتون
?واقعاعالی بودمنکه لذت بردم???
من یک سؤال دارم داخل منها ۷/0۰۵ منها ۰/۵۵۰ است چطور آخر ۷/۰۰ شد ۶/۰۰
سلام.
یک بار دیگر با دقت گامهای حل مثال را بررسی کنید.
سپاس از همراهیتان.
سلام ببخشید یه سوال داشتم عدد ده دهم همون یک میشه؟
سلام. ده دهم یعنی ده تقسیم بر ده که برابر با $$\frac{10}{10}=1$$ است.
از همراهیتان با مجله فرادرس، خوشحالیم.
سلام ببخشید در جمع ۳.۲۵بعلاوه ۰.۷۵بعلاوه ۵ چرا ۰.۷۵ صدم را تبدیل ب ۰.۰۷۵هزارم کردین ,آیا نباید صفر بعد از ۰.۷۵ قرارمیگرفت و جواب نهایی میشد ۹
سلام اعداد اعشاری به توان عدد اعشاری چگونه انجام میشود
۲.۷۱۸ به توان ۴.۵
سلام. عدد صورت سؤال ۰٫۰۷۵ بوده که به اشتباه ۰٫۷۵ نوشته شده بود. اصلاحات لازم انجام شد.
از همراهیتان با مجله فرادرس سپاسگزاریم.
سلام چرا در اخرین مثال ۵۳۹ تقسیم بر ۱۱شده؟؟
مگه ۱۱۰نبود؟؟
سلام.
متن تصحیح شد.
از همراهی و بازخورد شما سپاسگزاریم.
سلام. ببخشید میخواستم بدونم این ویدئو با چه نرم افزاری record شده است؟
سلام وقتی یه عددی رو به همراه اعشارش داریم آیا اون عددهای اعشارشم جزو چند رقمی بودن کل عدد حساب میشن مثلا۵۱۴۸۳۲۱/۰۰۹۳الآن این عدد چند رقمیه؟
عالی و رسا توضیح داده شده بود
ممنون از زحمات شما
سعید رسولی ،مهندس مکانیک و طراح